You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.3
Question 1.
Find the equation of a straight line passing through the mid-point of a line segment joining the points(1, -5) (4, 2) and parallel to
(i) X axis
(ii) Y axis
Solution:
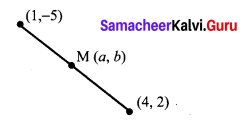

Question 2.
The equation of a straight line is 2(x – y) + 5 = 0. Find its slope, inclination and intercept on the Y axis.
Solution:
2(x – y) + 5 = 0
⇒ 2x – 2y + 5 =
⇒ 2y = 2x + 5

![]()
Question 3.
Find the equation of a line whose inclination is 30° and making an intercept – 3 on the Y axis.
Solution:
θ = 30°

Question 4.
Find the slope and y intercept of \(\sqrt{3}\)x + (1 – \(\sqrt{3}\))y = 3.
Solution:

![]()
Question 5.
Find the value of ‘a’, if the line through (-2, 3) and (8, 5) is perpendicular to y = ax = + 2
Solution:
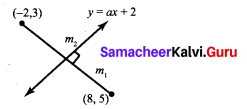
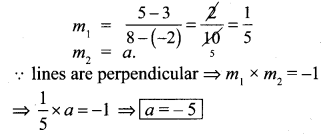
Question 6.
The hill in the form of a right triangle has its foot at (19, 3)The inclination of the hill to the ground is 45°. Find the equation of the hill joining the foot and top.
Solution:
θ = 45°
Coordinate of foot of hill = (19, 3) let equation of line be y = mx + c
m = tan θ = tan 45° = 1
⇒ y = x + c
Substituting y = 3 & x = 19, 3 = 19 + c ⇒ c = -16
![]()
Question 7.
Find the equation of a line through the given pair of points
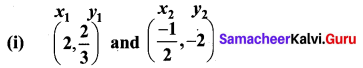
(ii) (2, 3) and (-7, -1)
Solution:
(i) Equation of the line in two point form is

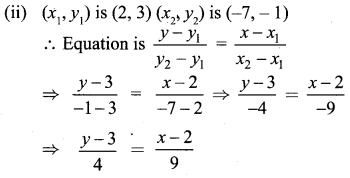
⇒ 9y – 27 = 4x – 8
⇒ 4x – 9y – 8 + 27 = 0
⇒ 4x – 9y + 19 = 0
![]()
Question 8.
A cat is located at the point(-6, -4) in xy plane. A bottle of milk is kept at (5, 11). The cat wish to consume the milk traveling through shortest possible distance. Find the equation of the path it needs to take its milk.
Solution:
A = (x1, y1) = (-6, -4)
B = (x2, y2) = (5, 11)
Shortest path between A and B is a line joining A and B.
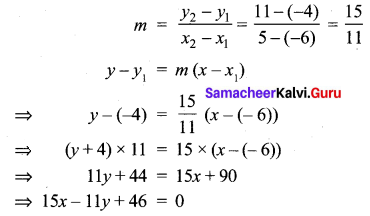
Question 9.
Find the equation of the median and altitude of ∆ABC through A where the vertices are A(6, 2) B(-5, -1) and C(1, 9)
Solution:
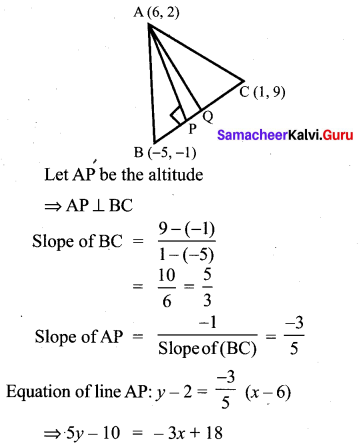

Question 10.
Find the equation of a straight line which -5 has slope \(\frac{-5}{4}\) and passing through the point (-1, 2).
Solution:
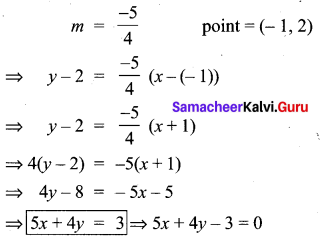
Question 11.
You are downloading a song. The percent y (in decimal form) of mega bytes remaining to get downloaded in x seconds is given by y = -0.1x + 1.
(i) graph the equation.
(ii) find the total MB of the song.
(iii) after how many seconds will 75% of the song gets downloaded?
(iv) after how many seconds the song will be downloaded completely?
Solution:
(i) y = -0.1x + 1
when x = 0 ⇒ y = 1
when y = 0 ⇒ y = 10
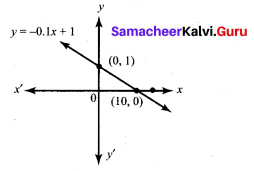
(ii) Total MB of song can be obtained when time = 0
∴ x = 0
⇒ y = 1 MB
(iii) time when 75% of song is downloaded
⇒ remaining % = 25% ⇒ y = 0.25
0.25 = -0. 1x + 1
⇒ 0.1x = 0.75
![]()
(iv) song will downloaded completely when , remaining % = 0 ⇒ y = 0
⇒ 0 = -0.1x + 1
⇒ x = 10
∴ 10 seconds
![]()
Question 12.
Find the equation of a line whose intercepts on the x and y axes are given below.
(i) 4, -6
(ii) \(-5 \frac{3}{4}\)
Solution:
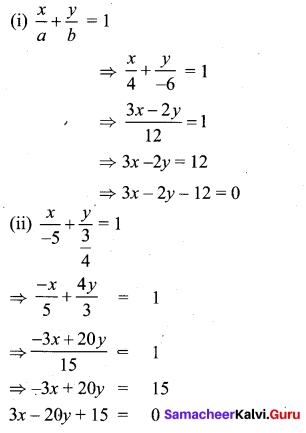
![]()
Question 13.
Find the intercepts made by the following lines on the coordinate axes,
(i) 3x – 2y – 6 = 0
(ii) 4x + 3y + 12 = 0
Solution:
(i) The given equation is
3x – 2y – 6 = 0
3x – 2y = 6
Divided by 6
\(\frac { 3x }{ 6 } \) – \(\frac { 2y }{ 6 } \) = \(\frac { 6 }{ 6 } \)
\(\frac { x }{ 2 } \) – \(\frac { y }{ 3 } \) = 1 ⇒ \(\frac { x }{ 2 } \) + \(\frac { y }{ -3 } \) = 1
(Comparing with \(\frac { x }{ a } \) + \(\frac { y }{ b } \) = 1)
∴ x intercept = 2; y intercept = -3
(ii) The given equation is
4x + 3y + 12 = 0
4x + 3y = -12
Divided by -12
\(\frac { 4x }{ -12 } \) + \(\frac { 3y }{ -12 } \) = \(\frac { -12 }{ -12 } \)
\(\frac { x }{ -3 } \) + \(\frac { y }{ -4 } \) = 1
(Comparing with \(\frac { x }{ a } \) + \(\frac { y }{ b } \) = 1)
∴ x intercept = -3; y intercept = -4
Question 14.
Find the equation of a straight line
(i) passing through (1, -4) and has intercepts which are in the ratio 2 : 5
(ii) passing through (-8, 4) and making equal intercepts on the coordinate axes
Solution:
(i) ratio of intercept = 2 : 5
