You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.16
Question 1.
In the matrix A = \(\left[\begin{array}{cccc}{8} & {9} & {4} & {3} \\ {-1} & {\sqrt{7}} & {\frac{\sqrt{3}}{2}} & {5} \\ {1} & {4} & {3} & {0} \\ {6} & {8} & {-11} & {1}\end{array}\right]\)
(i) The number of elements
(ii) The order of the matrix
(iii) Write the elements a22, a23, a24, a34, a43, a44
Solution:
(i) 16
(ii) 4 × 4
(iii) \(\sqrt{7}, \frac{\sqrt{3}}{2}\), 5, 0, -11, 1
Question 2.
If a matrix has 18 elements, what are the possible orders it can have? What if it has 6 elements?
Solution:
1 × 18, 2 × 9, 3 × 6, 6 × 3, 9 × 2, 18 × 1 and 1 × 6, 2 × 3, 3 × 2, 6 × 1
![]()
Question 3.
Construct a 3 × 3 matrix whose elements are given by then find the transpose of A.
(i) aij = |i – 2j|
(ii) aij = \(\frac{(i+j)^{3}}{3}\)
Solution:
(i) aij = |i – 2j|
a11 = |1 – 2 × 1| = |1 – 2| = |-1| = 1
a12 = |1 – 2 × 2| = |1 – 4| = |-3| = 3
a13 = |1 – 2 × 3| = |1 – 6| = |-5| = 5
a21 = |2 – 2 × 1| = |2 – 2| = 0
a22 = |2 – 2 × 2| = |2 – 4| = |-2| = 2
a23 = |2 – 2 × 3| = |2 – 6| = |-4| = 4
a31 = |3 – 2 × 1| = |3 – 2| = |1| = 1
a32 = |3 – 2 × 2| = |3 – 4| = |-1| = 1
a33 = |3 – 2 × 3| = |3 – 6| = |-3| = 3
∴ \(\left[\begin{array}{lll}{1} & {3} & {5} \\ {0} & {2} & {4} \\ {1} & {1} & {3}\end{array}\right]\) is the required 3 × 3 matrix

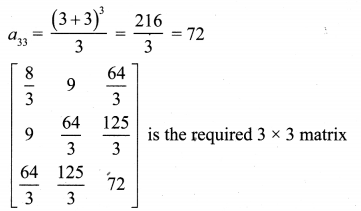
Question 4.

Solution:
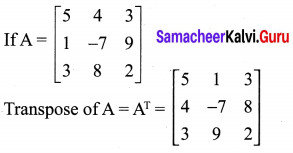
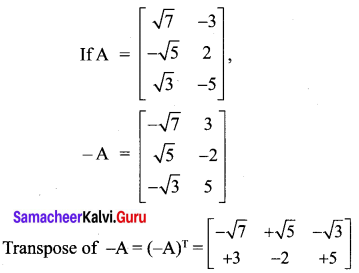
Question 5.
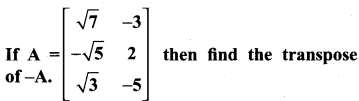
Solution:
![]()
Question 6.
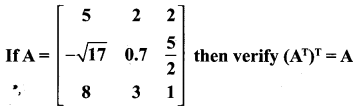
Solution:
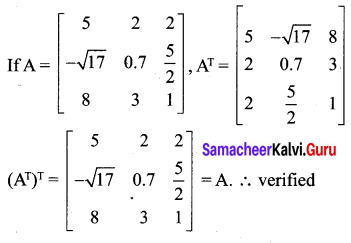
Question 7.
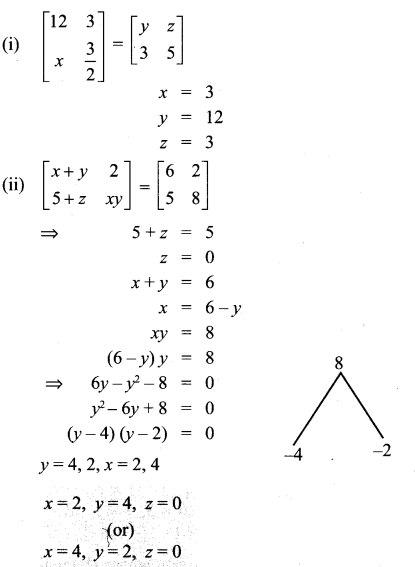
Find the values of x,y and z from the following equations

Solution: