You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Ex 2.7
Question 1.
Which of the following sequences are in G.P?
(i) 3, 9, 27, 81, ……..
(ii) 4, 44, 444, 4444, ………
(iii) 0.5, 0.05, 0.005, ……..
(iv) \(\frac { 1 }{ 3 } \),\(\frac { 1 }{ 6 } \),\(\frac { 1 }{ 12 } \)………
(v) 1, -5, 25, -125, …….
(vi) 120, 60, 30, 18, …….
(vii) 16, 4, 1, \(\frac { 1 }{ 4 } \), ……
Solution:
(i) 3, 9, 27, 81
r = Common ratio

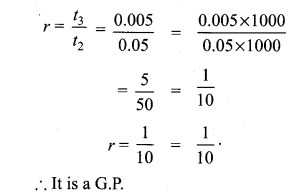


Question 2.
Write the first three terms of the G.P. whose first term and the common ratio are given below.
(i) a = 6, r = 3
(ii) a = \(\sqrt { 2 }\) , r = \(\sqrt { 2 }\)
(iii) a = 1000, r = \(\frac { 2 }{ 5 } \)
Solution:
(i) a = 6, r = 3
tn = arn-1
t1 = ar1-1 = ar0 = a = 6
t2 = ar2-1 = ar1 = 6 × 3 = 18
t3 = ar3-1 = ar2 = 6 × 32 = 54
∴ The 3 terms are 6, 18, 54, ….

The 3 terms are 1000, 400, 160, ……………
![]()
Question 3.
In a G.P. 729, 243, 81,… find t7.
Solution:
G.P = 729, 243, 81 ……
t7 = ?
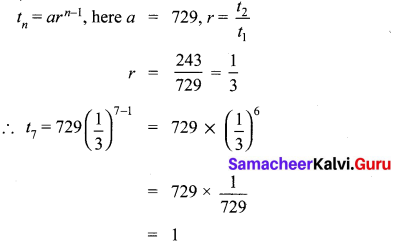
Question 4.
Find x so that x + 6, x + 12 and x + 15 are consecutive terms of a Geometric Progression.
Answer:
\(\frac{t_{2}}{t_{1}}\) = \(\frac { x+12 }{ x+6 } \),\(\frac{t_{3}}{t_{2}}\) = \(\frac { x+15 }{ x+12 } \)
Since it is a G.P.
\(\frac { x+12 }{ x+6 } \) = \(\frac { x+15 }{ x+12 } \)
(x + 12)2 = (x + 6) (x + 15)
x2 + 24x + 144 = x2 + 21x + 90
3x = -54 ⇒ x = \(\frac { -54 }{ 3 } \) = -18
Question 5.
Find the number of terms in the following G.P.
(i),4, 8, 16, …, 8192
(ii) \(\frac { 1 }{ 3 } \),\(\frac { 1 }{ 9 } \),\(\frac { 1 }{ 27 } \),……\(\frac { 1 }{ 2187 } \)
Solution:
(i) 4, 8, 16, …… 8192

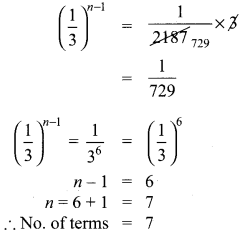
Question 6.
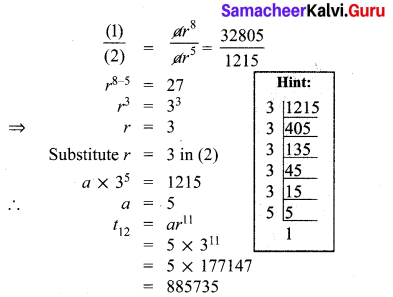
In a G.P. the 9th term is 32805 and 6th term is 1215. Find the 12th term.
Solution:
In a G.P
tn = arn-1
t9 = 32805
t6 = 1215
t12 = ?
Let
t9 = ar8 = 32805 ………(1)
t6 = ar5 = 1215 ………. (2)
Question 7.
Find the 10th term of a G.P. whose 8th term is 768 and the common ratio is 2.
Answer:
Here r = 2, t8 = 768
t8 = 768 (tn = arn-1)
a. r8-1 = 768
ar7 = 768 …..(1)
10th term of a G.P. = a.r 10-1
= ar9
= (ar7) × (r2)
= 768 × 22 (from 1)
= 768 × 4 = 3072
∴ 10th term of a G.P. = 3072
![]()
Question 8.
If a, b, c are in A.P. then show that 3a,3b,3c are in G.P.
Solution:
If a, b, c are in A.P
t2 – t1 = t3 – t2
b – a = c – b
2b = c + a
To prove that 3a, 3b, 3c are in G.P
⇒ 32b = 3c+a + a [Raising the power both sides]
⇒ 3b.3b = 3c.3a
\(\Rightarrow \frac{3^{b}}{3^{a}}=\frac{3^{c}}{3^{b}}\)
\(\Rightarrow \frac{t_{2}}{t_{1}}=\frac{t_{3}}{t_{1}}\)
⇒ Common ratio is same for 3a,3b,3c
⇒ 3a, 3b, 3c forms a G.P
∴ Hence it is proved .
Question 9.
In a G.P. the product of three consecutive terms is 27 and the sum of the product of two terms taken at a time is \(\frac { 57 }{ 2 } \). Find the three terms.
Solution:
Let the three consecutive terms in a G.P are \(\frac { a }{ r } \), a, ar.
Their Product = \(\frac { a }{ r } \) × a × ar = 27
a3 = 27 = 33
a = 3
Sum of the product of terms taken two at a time is \(\frac { 57 }{ 2 } \)
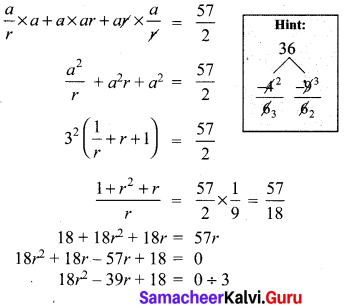
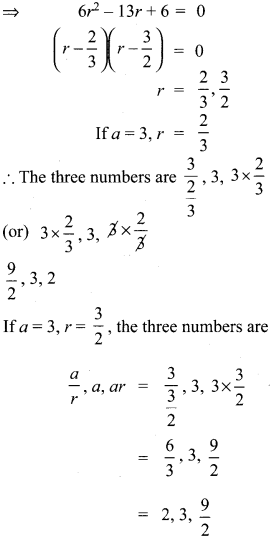
Question 10.
A man joined a company as Assistant Manager. The company gave him a starting salary of ₹60,000 and agreed to increase his salary 5% annually. What will be his salary after 5 years?
Solution:
Starting salary = ₹ 60,000
Increase per year = 5%
∴ At the end of 1 year the increase
= 60,0,00 × \(\frac { 5 }{ 100 } \)
₹ 3000
∴ At the end of first year his salary
= ₹ 60,000 + 3000
I year salary = ₹ 63,000
II Year increase = 63000 × \(\frac { 5 }{ 100 } \)
At the end of II year, salary
= 63000 + 3150
= ₹ 66150
III Year increase = 66150 × \(\frac { 5 }{ 100 } \)
= 3307.50
At the end of III year, salary = 66150 + 3307.50
= ₹ 69457.50
IV year increase = 69457.50 × \(\frac { 5 }{ 100 } \)
= ₹ 3472.87

![]()
Question 11.
Sivamani is attending an interview for a job and the company gave two offers to him. Offer A: ₹ 20,000 to start with followed by a guaranteed annual increase of 3% for the first 5 years.
Offer B: ₹ 22,000 to start with followed by a guaranteed annual increase of 3% for the first 5 years.
What is his salary in the 4th year with respect to the offers A and B?
Solution:
Offer A
Starting salary ₹ 20,000
Annual increase 6%

At the end of
III year ,salary = 22472 + 1348 = 23820
∴ IV year salary = ₹ 23820
Offer B
Starting salary = ₹ 22,000
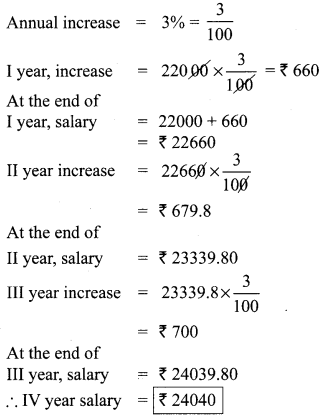
Salary as per Option A = ₹ 23820
Salary as per Option B = ₹ 24040
∴ Option B is better.
Question 12.
If a, b, c are three consecutive terms of an A.P. and x, y, z are three consecutive terms of a G.P. then prove that xb-c × yc-a × za-b = 1.
Solution:
a, b, c are three consecutive terms of an AP.
∴ Let a, b, c be a, a + d, a + 2d respectively ………… (1)
x, y, z are three consecutive terms of a GP.
∴ Assume x, y, z as x, x.r, x.r2 respectively ……… (2)
PT : xb-c , yc-a , za-b = 1
Substituting (1) and (2) in LHS, we get
LHS = xa+d-a-2d × (xr)a+2d-a × (xr2)a-a-d
= (x)-d . (xr)2d (xr2)-d
= \(\frac{1}{x^{d}}\) × x2d . r2d × \(\frac{1}{x^{d} r^{2 d}}\) = 1 = RHS