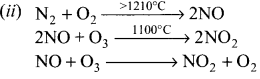Class 11

Students can Download Economics Chapter 6 Distribution Analysis Questions and Answers, Notes Pdf, Samacheer Kalvi 11th Economics Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Economics Solutions Chapter 6 Distribution Analysis

Samacheer Kalvi 11th Economics Distribution Analysis Text Book Back Questions and Answers

Part – A
Multiple Choice Questions

Question 1.
In Economics, distribution of income is among the
(a) factors of production
(b) individual
(c) firms
(d) traders
Answer:
(a) factors of production

Question 2.
Theory of distribution is popularly known as ………………………..
(a) Theory of product – pricing
(b) Theory of factor – pricing
(c) Theory of wages
(d) Theory of Interest
Answer:
(b) Theory of factor-pricing

Question 3.
Rent is the reward for the use of
(a) capital
(b) labour
(c) land
(d) organization
Answer:
(c) land

Question 4.
The concept of ‘Quasi – Rent’ is associated with ………………………
(a) Ricardo
(b) Keynes
(c) Walker
(d) Marshall
Answer:
(d) Marshall

Question 5.
The Classical Theory of Rent was propounded by
(a) Ricardo
(b) Keynes
(c) Marshall
(d) Walker
Answer:
(a) Ricardo

Question 6.
‘Original and indestructible powers of the soil’ is the term used by ……………………….
(a) J.S.Mill
(b) Walker
(c) Clark
(d) Ricardo
Answer:
(d) Ricardo

Question 7.
The reward for labour is
(a) rent
(b) wage
(c) profit
(d) interest
Answer:
(b) wage

Question 8.
Money wages are also known as ……………………….
(a) Real wages
(b) Nominal wages
(c) Original wages
(d) Transfer wages
Answer:
(b) Nominal wages

Question 9.
Residual Claimant Theory is propounded by
(a) Keynes
(b) Walker
(c) Hawley
(d) Knight
Answer:
(b) Walker

Question 10.
The reward is given for the use of capital ………………………
(a) Rent
(b) Wage
(c) Interest
(d) Profit
Answer:
(c) Interest

Question 11.
Keynesian Theory of interest is popularly known as
(a) Abstinence Theory
(b) Liquidity Preference Theory
(c) Loanable Funds Theory
(d) Agio Theory
Answer:
(b) Liquidity Preference Theory

Question 12.
According to the Loanable Funds Theory, supply of loanable funds is equal to …………………………
(a) S + BC + DH + DI
(b) I + DS + DH + BM
(c) S+ DS + BM+ DI
(d) S + BM + DH + DS
Answer:
(a) S + BC + DH + DI

Question 13.
The concept of meeting unexpected expenditure according to Keynes is
(a) Transaction motive
(b) Precautionary motive
(c) Speculative motive
(d) Personal motive
Answer:
(b) Precautionary motive

Question 14.
The distribution of income or wealth of a country among the individuals are ………………………….
(a) Functional distribution
(b) Personal distribution
(c) Goods distribution
(d) Services distribution
Answer:
(b) Personal distribution

Question 15.
Profit is the reward for
(a) land
(b) organization
(c) capital
(d) labour
Answer:
(b) organization

Question 16.
Innovation Theory of profit was given by …………………………..
(a) Hawley
(b) Schumpeter
(c) Keynes
(d) Knight
Answer:
(b) Schumpeter

Question 17.
Quasi-rent arises in
(a) Man-made appliances
(b) Homemade items
(c) Imported items
(d) None of these
Answer:
(a) Man-made appliances

Question 18.
“Wages as a sum of money are paid under contract by an employer to a worker for service rendered”- Who said this?
(a) Benham
(b) Marshall
(c) Walker
(d) J.S.Mill
Answer:
(a) Benham

Question 19.
Abstinence Theory of Interest was propounded by
(a) Alfred Marshall
(b) N.W Senior
(c) Bohm-Bawerk
(d) Knut Wicksell
Answer:
(b) N.W Senior

Question 20.
Loanable Funds Theory of Interest is called as …………………………
(a) Classical Theory
(b) Modem Theory
(c) Traditional Theory
(d) Neo-Classical Theory
Answer:
(d) Neo-Classical Theory

Part – B
Answer the following questions in one or two sentences

Question 21.
What is meant by distribution?
Answer:
Distribution means division of income among the four factors of production in terms of rent to landlords, wage to labourer, interest to capital and profit to entrepreneurs. The theory of functional distribution deals with how the relative prices of these factors of production are determined. The theory of factor prices is popularly known as the theory of distribution.

Question 22.
Mention the types of distribution?
Answer:
Personal Distribution: Personal Distribution is the distribution of national income among individuals.
Functional Distribution: Functional Distribution means the distribution of income among the four factors of production namely land, labour, capital and organization for their services in the production process.

Question 23.
Define ‘Rent’.
Answer:
Rent is the price or reward given for the use of land or house or a machine to the owner But, in Economics, “Rent” or “Economic Rent” refers to that part of the payment made by a tenant to his landlords for the use of land only.

Question 24.
Distinguish between real and money wages.
Answer:
Real wages :
Wages paid in terms of goods and services. It refers to the purchasing power of money wages.

Money wages :
Nominal wages are referred to as wages paid in terms of money.

Question 25.
What do you mean by interest?
Answer:
Interest is the price paid for the use of capital in any market.

Question 26.
What is profit?
Answer:
Profit is the amount left with the entrepreneur after he has made payments for all the other factors of production.

Question 27.
State the meaning of liquidity preference?
Answer:

1. Liquidity preference means the preference of the people to hold wealth in the form of liquid cash rather than in other non – liquid assets like bonds, securities, bills of exchange, land, building, gold etc.
2. “Liquidity Preference is the preference to have an amount of cash rather than of claims against others”.

Part – C
Answer the following questions in One Paragraph

Question 28.
What are the motives of demand for money?
Answer:
1. Transaction motive :
It relates to the desire of the people to hold cash for the current transactions.
Mt=f (y)

2. Precautionary motive :
It relates to the desire of the people to hold cash to meet unexpected or unforeseen expenditures.
Mp = f (y)

3. Speculative motive :
It relates to the desire of the people to hold cash in order to take advantage of market movements regarding future changes in the price of bonds and securities in the capital market.
Ms = f (i)

Question 29.
List out the kinds of wages:
Answer:
Wages are divided into four types.

1. Nominal Wages or Money Wages: Nominal wages are referred to the wages paid in terms of money.
2. Real Wages: Real wages are the wages paid in terms of goods and services. Hence, real wages are the purchasing power of money wages.
3. Piece Wages: Wages that are paid on the basis of quantum of work done.
4. Time Wages: Wages that are paid on the basis of the amount of time that the worker works.

Question 30.
Distinguish between rent and quasi-rent
Answer:
Rent:

1. Rent accrues to land
2. The supply of land is fixed forever
3. It enters into price

Quasi – rent:

1. Quasi-rent accrues to man-made appliances
2. The supply of man made appliances is fixed for a short period only
3. It does not enter into price.

Question 31.
Briefly explain the Subsistence Theory of Wages?
Answer:
The subsistence theory of wages:

1. Subsistence theory of wages is one of the oldest theories of wages.
2. According to this theory, wage must be equal to the subsistence level of the labourer and his family.
3. Subsistence means the minimum amount of food, clothing and shelter which workers and their family require for existence.
4. If workers are paid higher wages than the subsistence level, the workers would be better off and they will have large families.
5. Hence, the population would increase.
6. When the population increases, the supply of labourer would increase and therefore, wages will come down.
7. If wages are lower than the subsistence level, there would be a reduction in population and thereby the supply of labour falls and wages increase to the subsistence level.

Question 32.
State the Dynamic Theory of Profit.
Answer:

1. This theory was propounded by the American economist J.B.Clark in 1900.
2. Profit is the reward for dynamic changes in society.
3. Static society is one where everything is stationary or stagnant and there is no change at all.
4. There is no role for an entrepreneur in a static society.
5. According to Clark, the following five main changes are taking place in a dynamic society.
   • Population is increasing
   • Volume of Capital is increasing
   • Methods of production are impro ving
   • Forms of industrial organization are changing
   • The wants of consumer are multiplying

Question 33.
Describe briefly the Innovation Theory of Profit?
Answer:
Innovation Theory of Profit:

1. The innovation theory of profit was propounded by Joesph. A.Schumpeter.
2. Schumpeter says an entrepreneur is not only an undertaker of a business but also an innovator in the process of production.
3. Profit is the reward for “innovation”.
4. According to Schumpeter, an innovation may consist of the following:
   • Introduction of a new product.
   • Introduction of a new method of production.
   • Opening up of a new market.
   • Discovery of new raw materials
   • Reorganization of an industry/firm.

When any one of these innovations is introduced by an entrepreneur, it leads to a reduction in the cost of production and thereby brings profit to an entrepreneur. To obtain profit continuously, the innovator needs to innovate continuously. The real innovators do so. Imitative entrepreneurs cannot innovate.

Question 34.
Write a note on the Risk-bearing Theory of Profit.
Answer:

• Risk bearing theory of profit was propounded by the American economist F.B. Hawley in 1907.
• According to him, profit is the reward of “risk-taking” in business.
• Risk-taking is an essential function of the entrepreneur and is the basis of profits.
• It is a well-known fact that every business involves some risks.
• Since the entrepreneur undertakes the risks, he receives profit.
• If the entrepreneur does not receive the reward, he will not be prepared to undertake the risks.
• Every entrepreneur produces goods in anticipation of demand.
• It is the profit that induces the entrepreneurs to undertake such risks.

Part – D
Answer the following questions in about a page

Question 35.
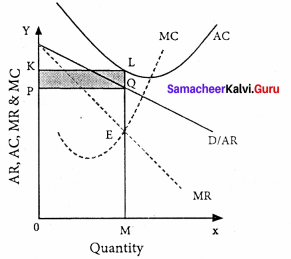
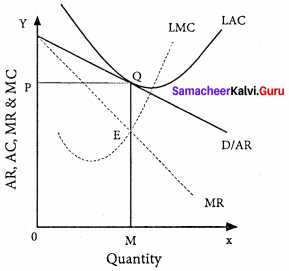
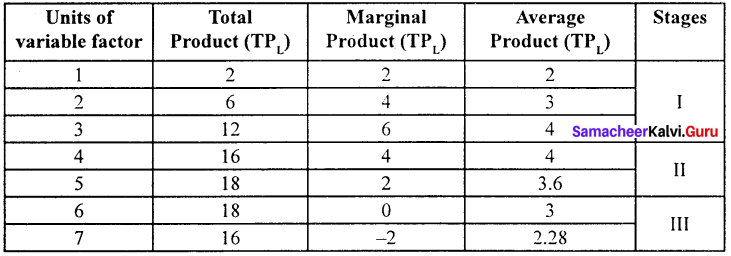
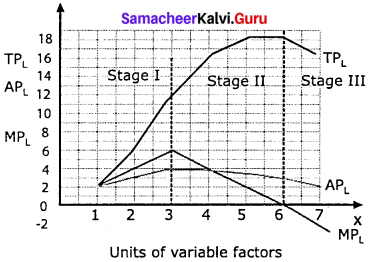
Explain the Marginal Productivity Theory of Distribution.
Answer:
Marginal productivity theory of distribution was developed by Clark, Wicksteed and Walras. This theory explains how the prices of various factors of production are determined. This theory is also known as the “General theory of distribution” or “National dividend theory of distribution”.
Assumptions:

1. All the factors of production are homogenous and can be substituted for each other.
2. There is perfect competition in both factor and product market.
3. There is perfect mobility and full employment of factors of production.
4. This theory is applicable only in the long-run.
5. The entrepreneurs aim at profit maximization.
6. There is no government intervention and no technological change.

Explanation of the theory :
Each factor is rewarded according to its marginal productivity.

Marginal product:
The marginal product of a factor of production means the addition made to the total product by employment of an additional unit of that factor.

Marginal physical product (MPP) :
The MPP of a factor is the increment in the total product obtained by the employment of an additional unit of that factor.

Value of marginal product (VMP):
VMP = MPP x price

Statement of the theory:

1. The price of a factor of production depends upon its productivity.
2. The price of a factor is determined by and will be equal to the marginal revenue product of that factor.
3. Under certain conditions, the price of a factor will be equal to both the average and marginal products of that factor.

Marginal productivity under perfect competition:

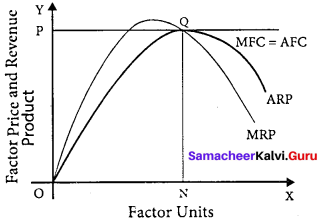
The X-axis represents factor units and Y-axis represents the factor price and revenue product.
MRP – Marginal Revenue Product Curve
ARP – Average Revenue Product Curve
AFC – Average Factor Cost Curve
MFC – Marginal Factor cost Curve
AFC – is horizontal under perfect competition and MFC coincides with it.
When there is perfect competition in the factor market, the firm is in equilibrium only when MFC = MRP
At the point Q by employing ON units of factors and paying OP price (NQ) where MFC = MRP
At Q, MRP = ARP
Price of the factor (NQ) = Marginal revenue
Product (NQ) = Average revenue product (NQ)
There is no exploitation of factors under perfect competition.
Beyond point Q the price paid to the factor is more than the marginal revenue product and average revenue product, so employers do not employ the factors.

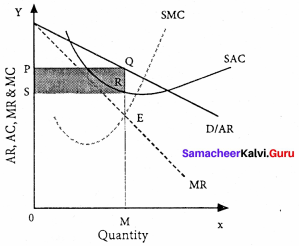
Question 36.
Illustrate the Ricardian Theory of Rent.
Answer:
The classical theory of rent is called the “Ricardian theory of rent”.
Definition:
Rent is that portion of the produce of the earth which is paid to the landlord for the use of the original and indestructible powers of the soil.

Assumptions:

1. Land differs infertility.
2. The law of diminishing returns operates in agriculture.
3. Rent depends upon the fertility and location of the land.
4. The theory assumes perfect competition and a long period.
5. There is the existence of marginal land or no-rent land.
6. The land has certain “Original and indestructible powers”.
7. The land is used for cultivation only.
8. Most fertile lands are cultivated first.

Statement of the theory with an illustration:
Assume that some people settle on the newly discovered island. People will first cultivate the most fertile ‘A’ grade land. They produce 40 bags of paddy.

Suppose after some time if another group of people settles down on the same island. They cultivate ‘B’ grade land which produces 30 bags of paddy. Suppose yet another group of people settle down there they cultivate ‘C’ grade land. It produces 20 bags of paddy.

This surplus of ‘A’ grade land is now raised to 20 bags (40 – 20) and it is the ‘Economic Rent’ of ‘A’ grade land. The surplus of ‘B’ grade land is 10 bags (30 – 20). In ‘C’ grade land cost of production is equal to the price of its products and it does not yield any rent (20 – 20). Hence ‘C’ grade land is called ‘no-rent land’ or marginal land.

The land which yields rent is called “intra-marginal land”.
Rent indicates the differential advantage of the superior land over the marginal land.
Ricardian Theory’ of Rent :

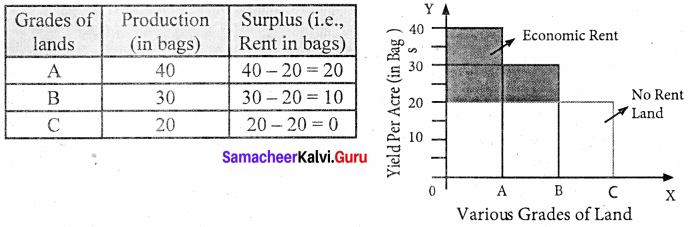
Diagrammatic illustration:
The X-axis represents various grades of land and the Y-axis yield per acre (in bags). OA, AB, and BC are the ‘A’, ‘B’, ‘C’ grade lands respectively.

The ‘C’ grade land is the no-rent land. A and B grade lands are “intra-marginal lands. The economic rent yielded by ‘A’ and ‘B’ grade lands is equal to the shaded area of their respective rectangles.

Criticisms:

1. The order of cultivation from most fertile to least fertile lands is historically wrong.
2. This theory assumes that rent does not enter into price. But in reality, rent enters into the price.

Question 37.
Elucidate the Loanable Funds Theory of Interest.
Answer:

1. The Loanable Funds Theory, also known as the “Neo-Classical Theory,” was developed by Swedish economists like Wicksell, Bertil, Ohlin, Viner, Gunnar Myrdal, and others.
2. According to this theory, interest is the price paid for the use of loanable funds.
3. The rate of interest is determined by the equilibrium between the demand for and supply of loanable funds in the credit market.

Demand for Loanable Funds
The demand for loanable funds depends upon the following:

1. Demand for Investment [I]

• The most important factor responsible for the loanable funds is the demand for investment.
• The bulk of the demand for loanable funds comes from business firms which borrow money for purchasing capital goods.

2. Demand for consumption [C]

• The demand for loanable funds comes from individuals who borrow money for consumption purposes also.

3. Demand for Hoarding [H]

• The next demand for loanable funds comes from hoarders. Demand for hoarding money arises because of people’s preference for liquidity, idle cash balances, and so on.
• The demand for C, I, and H varies inversely with the interest rate.

Equilibrium:
The rate of interest is determined by the equilibrium between the total demand for and the total supply of loanable funds.
Supply of loanable funds = S + BC + DH + DI
Demand for loanable funds = I + C + H

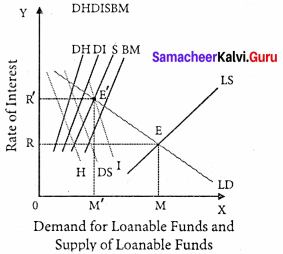
Supply of Loanable funds:
The supply of loanable funds depends upon the following four sources:

1. Savings [S]: Loanable funds comes from savings. According to this theory, savings may be of two types, namely,

• Savings planned by individuals are called “ex-ante-savings ”.
• The unplanned savings are called ‘ex-post savings”.

2. Bank Credit [BC]: Bank credit is another source of loanable funds. Commercial banks create credit and supply loanable funds to the investors.

3. Dishoarding [DH]: Dishoarding means bringing out the hoarded money into use and thus it constitutes a source of supply of loanable funds.

4. Disinvestment: [DI]: Disinvestment is the opposite of investment. Disinvestment means not providing sufficient funds for the depreciation of equipment.

It gives rise to the supply of loanable funds.
All four sources of supply of loanable funds vary directly with the interest rate.

Question 38.
Explain the Keynesian Theory of Interest.
Answer:
According to Keynes, interest is the reward for parting with liquidity’ for a specified period of time.
Meaning of liquidity preference:
Liquidity preference means the preference of the people to hold wealth in the form of liquid cash rather than in other non-liquid assets.
Motives of demand for money:
The three motives of liquidity preference are.

1. The transaction motive M_t = f (y)
2. The precautionary motive M_p = f (y)
3. The speculative motive M_s = f (i)

Determination of Rate of Interest:
According to Keynes, the rate of interest is determined by the demand for and the supply of money. The demand for money is liquidity preference. The supply of money is determined by the policies of the government and the central bank.

Equilibrium between demand and supply of money:
The equilibrium between liquidity preference and demand for money determine the rate of interest. In short-run, the supply of money is assumed to be constant.

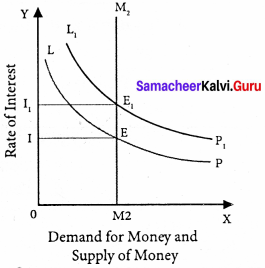
LP is the liquidity preference curve. M₂ shows the supply curve of money to satisfy speculative motive. Both curves intersect at the point E which is the equilibrium. Here, rate of interest is I.

If liquidity preference increases from LP to L₁ P₁ the supply of money remains constant, the rate of interest increase from OI to OI₁

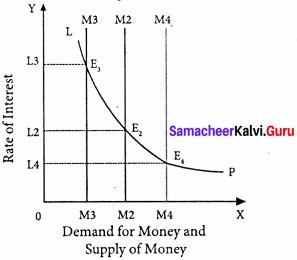
Suppose LP remains constant. If the supply of money is OM₂, the interest is OI₂ and if the supply of money is reduced from OM₂ to OM₂, the interest would increase from OM₂ to OM₄. If the supply of money is increased from OM₂ to OM₄ the interest would decrease from OI₂ to Ol₄

Criticisms:

1. This theory does not explain the existence of different interest rates prevailing in the market at the same time.
2. It explains interest rate only in the short – run.

Samacheer Kalvi 11th Economics Distribution Analysis Additional Questions and Answers

Part -A
Choose the best options

Question 1.
Marginal Productivity theory is the …………………….. theory of distribution.
(a) Average
(b) Marginal
(c) Liquidity preference theory
(d) General
Answer:
(d) General

Question 2.
“Interest is the price paid for the use of capital in any market” is said by_______
(a) Adam Smith
(b) Torrance
(c) Walker
(d) Marshall
Answer:
(d) Marshall

Question 3.
The standard of living of workers in a country depends upon the ……………………… wages.
(a) Real
(b) Effective
(c) Direct
(d) Elastic
Answer:
(a) Real

Question 4.
The author of the agio-theory of interest.
(a) N.W. Senior
(b) Bohm Bawerk
(c) Walker
(d) Marshall
Answer:
(b) Bohm Bawerk

Question 5.
Who propounded the risk-bearing theory of profit?
(a) Bohm – Bawerk
(b) F.B Hawley
(c) Marshall
(d) Walker
Answer:
(b) F.B Hawley

Question 6.
The dynamic theory of profit was propounded by_______
(a) Marshall
(b) J.B.Clark
(c) J.M. Keynes
(d) Walker
Answer:
(b) J.B.Clark

Question 7.
What is meant by MPS?
(a) Marginal production supply
(b) Marginal production sale
(c) Marginal production service
(d) Marginal propensity to save
Answer:
(d) Marginal propensity to save

Question 8.
Time preference theory was given by_______
(a) John Ray
(b) Bohm Bawerk
(c) F.B. Hawley
(d) Irving Fisher
Answer:
(d) Irving Fisher

Question 9.
The demand for labour is ………………………
(a) Effective demand
(b) Direct demand
(c) Derived demand
(d) Elastic demand
Answer:
(c) Derived demand

Question 10.
_______ is the author of the modern theory of rent
(a) Joan Robinson
(b) Boulding
(c) Both
(d) None
Answer:
(c) Both

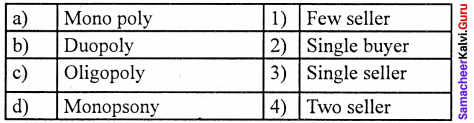
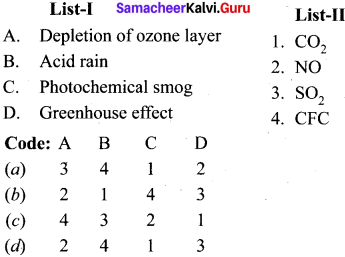
Match the following and choose the answer using the codes given below

Question 1.

(a) 3 4 2 1
(b) 4 3 1 2
(c) 1 2 3 4
(d) 2 3 4 1
Answer:
(c) 1 2 3 4

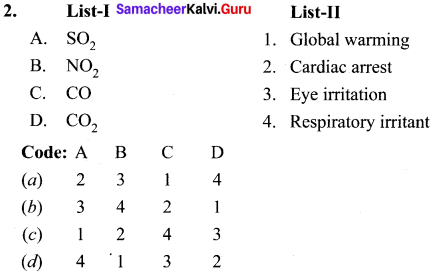
Question 2.

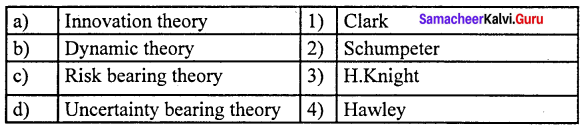
(a) 2 1 4 3
(b) 1 4 2 3
(c) 1 2 3 4
(d) 4 1 3 2
Answer:
(a) 2 1 4 3

Choose the incorrect pair

Question 3.

Answer:
(d) Total demand for money (iv) Mt + Mp

Question 4.

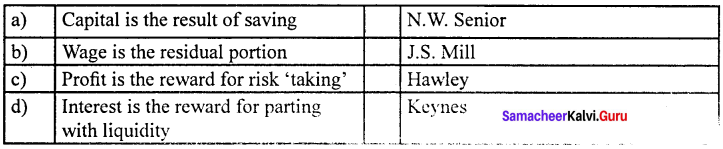
Answer:
(b) Wage is the residual portion (ii), J.S. Mill

Choose the correct statement

Question 5.
(a) The supply of land is fixed forever
(b) Quasi-rent accrues to land
(c) The supply of man-made appliances are fixed
(d) Quasi-rent enters price
Answer:
(a) The supply of land is fixed forever

Question 6.
(a) Rent is the reward for labour
(b) Profit is the reward for labour
(c) Wages are the reward for labour
(d) Interest is the reward for organization
Answer:
(b) Profit is the reward for labour

Choose the odd one out

Question 7.
(a) Bank credit
(b) Hoarding
(c) Dishoarding
(d) Disinvestment
Answer:
(b) Hoarding

Question 8.
(a) Monopoly profit
(b) Windfall profit
(c) Functional reward
(d) Reward for labourer
Answer:
(d) Reward for labourer

Question 9.
(a) Nominal wages
(b) Real wages
(c) Direct wages
(d) Piece wages
Answer:
(c) Direct wages

Question 10.
(a) Abstinence theory
(b) Loanable funds theory
(c) Liquidity preference theory
(d) Risk bearing theory
Answer:
(b) Loanable funds theory

Analyze the reason for the following

Question 11.
Assertion (A) : Demand for loanable funds depends on investment, consumption, and hoarding.
Reason (R) : The supply of loanable funds depends on hoarding and investment.
(a) (A) and (R) are true, (R) is not the correct explanation of (A)
(b) (A) and (R) are true, (R) is the correct explanation of (A)
(c) (A) is true (R) are false.
(d) (A) is false (R) is true.
Answer:
(c) (A) is true (R) are false.

Question 12.
Assertion (A) : The rate of interest is determined by the demand for money and the supply of money.
Reason (R) : The demand for money is liquidity preference.
(a) Both (A) and (R) are true, (R) is not the correct explanation of (A)
(b) Both (A) and (R) are correct, (R) is the correct explanation of (A)
(c) Both (A) and (R) are false.
(d) (A) is false and (R) is true.
Answer:
(a) Both (A) and (R) are true, (R) is not the correct explanation of (A)

Question 13.
Assertion (A) : Only superior land get rent
Reason (R) : Rent arose on account of differences in the fertility of the land.
(a) Both (A) and (R) are true
(b) Both (A) and (R) are a false correct explanation of (A)
(c) (A) is true and (R) are false.
(d) (A) is false and (R) is true.
Answer:
(a) Both (A) and (R) are true

Choose the incorrect pair

Question 14.

Answer:
(d) Wage fund theory (iv) J.S. Mill

Question 15.

Answer:
(b) Wages (ii) Labour

Fill in the blanks with the suitable option given below

Question 16.
F.A. Walker wrote a book ______ in 1875.
(a) Political economy
(b) Social economy
(c) Principles of economics
(d) Wealth of nations
Answer:
(a) Political economy

Question 17.
The author of Agio theory of interest______
(a) N.W. Seniors
(b) Bohm-Bawerk
(c) Walker
(d) Marshall
Answer:
(b) Bohm-Bawerk

Question 18.
______ is the produced means of production.
(a) Land
(b) Labour
(c) Capital
(d) Organisation
Answer:
(c) Capital

Choose the best option

Question 19.
The theory of factor prices is popularly known as the theory of
(a) Distribution
(b) Exchange
(c) Wages
(d) Profit
Answer:
(a) Distribution

Question 20.
______ is the author of the modern theory of rent
(a) Joan Robinson
(b) Boulding
(c) Both
(d) None
Answer:
(c) Both

Part – B
Answer the following questions in one or two sentences

Question 1.
What is the theory of distribution?
Answer:
The theory of factor prices is popularly known as the theory of distribution.

Question 2.
Define VMP?
Answer:

1. VMP – means Value of Marginal Product.
2. The Value of the Marginal Product is obtained by multiplying the Marginal Physical Product of the factor by the price of the product. Symbolically, VMP = MPP x Price.

Question 3.
Define the Marginal productivity theory of distribution.
Answer:
The theory states that price or the reward for any factor of production is equal to the marginal productivity of that factor.

Question 4.
What is the marginal product? Define marginal physical product ?
Answer:
The addition made to the total product by the employment of an additional unit of that factor.

Question 5.
Define modern theory of rent.
Answer:
Rent is the difference between the actual earnings of a factor of production and its transfer earning.
Rent = Actual earning – Transfer earning

Question 6.
What is “Wage Fund“.
Answer:
According to Mill, “Every employer will keep a given amount of capital for payment to the workers”. It is known as the “Wage Fund”.

Question 7.
Define Quasi Rent.
Answer:
“Quasi rent is the income derived from machines and other appliances made by man
QR = Total revenue – Total variable cost

Part – C
Answer the following questions in One Paragraph

Question 1.
Explain the types of distribution.
Answer:
1. Personal distribution: It is the distribution of national income among individuals.
2. Functional distribution: It means the distribution of income among the four factors of production for their services in the production process.

Question 2.
Explain the standard of living theory of wages.
Answer:
This theory of wages was developed by Torrance is an improved version of the subsistence theory of wage. According to this theory, the wage is equal to the standard of living of the workers. If the standard of living is high, wages will be high and vice versa. The standard of a living wage means the amount necessary to maintain the labourer in the standard of life to which he is accustomed.

Question 3.
Briefly explain the Abstinence theory or waiting theory?
Answer:

1. This theory was propounded by N.W.Senior.
2. According to Senior, capital is the result of saving.
3. Saving involves “abstinence” or “Sacrifice”
4. It is possible to save only if one abstains from present consumption.
5. Interest is the reward or compensation paid to the saver (capitalist) for his “abstinence” or “sacrifice”.
6. Marshall accepted the Abstinence theory of interest.
7. According to him, interest is a reward for waiting.
8. Saving involves waiting.
9. Therefore, interest is the reward paid to the saver for his “ waiting ”.

Question 4.
State the theories of interest.
Answer:

1. Abstinence theory or waiting theory.
2. Agio theory or the psychological theory.
3. Loanable funds theory or the neoclassical theory.
4. Liquidity preference theory or the monetary theory.

Question 5.
What are the four sources of loanable funds?
Answer:
The supply of loanable funds depends upon the following four sources.

1. Savings (S)
2. Bank Credit (BC)
3. Dishoarding (DH)
4. Disinvestment (DI)

Question 6.
What are the kinds of profit?
Answer:
1. Monopoly profit:
Profit earned by the firm because of its monopoly control.

2. Windfall profit:
Some times, profit arises due to changes in the price level. Profit is due to unforeseen factors.

3. Profit as a functional reward:
Just like rent, wage and interest, profit is earned by the entrepreneur for his entrepreneurial function.

Question 7.
State the residual claimant theory of wage.
Answer:
This theory was propounded by the American economist F.A. Walker in 1875, in his book political economy. According to this theory, wage is the residual portion after paying the remuneration of all the other three factors namely land capital and organization.

Criticisms:

1. This theory does not explain the role of trade unions can secure higher wages for workers.
2. The demand-side of labour in the determination of wages needs to be considered.

Students can Download Economics Chapter 5 Market Structure and Pricing Questions and Answers, Notes Pdf, Samacheer Kalvi 11th Economics Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Economics Solutions Chapter 5 Market Structure and Pricing

Samacheer Kalvi 11th Economics Market Structure and Pricing Text Book Back Questions and Answers

Part – A

Multiple Choice Questions

Question 1.
In which of the following is not a type of market structure Price will be very high?
(a) Perfect competition
(b) Monopoly
(c) Duopoly
(d) Oligopoly
Answer:
(a) Perfect competition

Question 2.
Equilibrium condition of a firm is …………………….
(a) MC = MR
(b) MC > MR
(c) MC < MR
(d) MR = Price
Answer:
(a) MC = MR

Question 3.
Which of the following is a feature of monopolistic competition?
(a) One seller
(b) Few sellers
(c) Product differentiation
(d) No entry
Answer:
(c) Product differentiation

Question 4.
A firm under monopoly can earn ………………… in the short run.
(a) Normal profit
(b) Loss
(c) Supernormal profit
(d) More loss
Answer:
(c) Supernormal profit

Question 5.
There is no excess capacity under ______
(a) Monopoly
(b) Monopolistic competition
(c) Oligopoly
(d) Perfect competition
Answer:
(d) Perfect competition

Question 6.
Profit of a firm is obtained when ……………………
(a) TR < TC (b) TR – MC (c) TR > TC
(d) TR = TC
Answer:
(c) TR > TC

Question 7.
Another name of price is ______
(a) Average Revenue
(b) Marginal Revenue
(c) Total Revenue
(d) Average Cost
Answer:
(a) Average Revenue

Question 8.
In which type of market, AR and MR are equal ………………………
(a) Duopoly
(b) Perfect competition
(c) Monopolistic competition
(d) Oligopoly
Answer:
(b) Perfect competition

Question 9.
In monopoly, MR curve lies below ______
(a) TR
(b) MC
(c) AR
(d) AC
Answer:
(c) AR

Question 10.
Perfect competition assumes ……………………..
(a) Luxury goods
(b) Producer goods
(c) Differentiated goods
(d) Homogeneous goods
Answer:
(d) Homogeneous goods

Question 11.
Group equilibrium is analysed in ______
(a) Monopolistic competition
(b) Monopoly
(c) Duopoly
(d) Pure competition
Answer:
(a) Monopolistic competition

Question 12.
In monopolistic competition, the essential feature is …………………….
(a) Same product
(b) Selling cost
(c) Single seller
(d) Single buyer
Answer:
(b) Selling cost

Question 13.
Monopolistic competition is a form of ______
(a) Oligopoly
(b) Duopoly
(c) Imperfect competition
(d) Monopoly
Answer:
(c) Imperfect competition

Question 14.
Price leadership is the attribute of ………………………
(a) Perfect competition
(b) Monopoly
(c) Oligopoly
(d) Monopolistic competition
Answer:
(c) Oligopoly

Question 15.
Price discrimination will always lead to ______
(a) Increase in output
(b) Increase in profit
(c) Different prices
(d) b and c
Answer:
(d) b and c

Question 16.
The average revenue curve under monopolistic competition will be …………………….
(a) Perfectly inelastic
(b) Perfectly elastic
(c) Relatively elastic
(d) Unitary elastic
Answer:
(c) Relatively elastic

Question 17.
Under perfect competition, the shape of demand curve of a firm is ______
(a) Vertical
(b) Horizontal
(c) Negatively sloped
(d) Positively sloped
Answer:
(b) Horizontal

Question 18.
In which market form, does absence of competition prevail?
(a) Perfect competition
(b) Monopoly
(c) Duopoly
(d) Oligopoly
Answer:
(b) Monopoly

Question 19.
Which of the following involves maximum exploitation of consumers?
(a) Perfect competition
(b) Monopoly
(c) Monopolistic competition
(d) Oligopoly
Answer:
(b) Monopoly

Question 20.
An example of selling cost is ………………………
(a) Raw material cost
(b) Transport cost
(c) Advertisement cost
(d) Purchasing cost
Answer:
(c) Advertisement cost

Part – B

Answer the following questions in one or two sentences

Question 21.
Define Market.
Answer:

1. Market refers to a physical place, where commodities and services are bought and sold. In Economics, the term “market” refers to a system of exchange between the buyers and the sellers of a commodity.
2. Besides direct exchanges, there are exchanges that are carried out through correspondence, telephones, online, e-mail, etc.

Question 22.
Who is price – taker?
Answer:
A large number of buyers’ implies that each individual buyer buys a very, very small quantum of a product as compared to that found in the market. This means that he has no power to fix the price of the product. He is only a price taker and not a price-maker.

Question 23.
Point out the essential features of pure competition.
Answer:
Features of the Perfect Combination:

1. A large number of Buyers and Sellers.
2. Homogeneous Product and Uniform Price.
3. Free Entry and Exit.
4. Absence of Transport Cost.
5. Perfect Mobility of Factors of Production.
6. Perfect knowledge of the Market.
7. No Government Intervention.

Question 24.
What is selling costs?
Answer:

1. Selling Cost is the discussion of “ Product differentiation”.
2. We can infer that the producer under monopolistic competition has to incur expenses to popularize his brand.
3. This involved in selling the product is called selling cost.
4. According to Prof. Chamberlin, selling cost is “The cost incurred in order to alter the position or shape of the demand curve for a product”.

Question 25.
Draw demand curve of a firm for the following:
Answer:
(a) Perfect Competition
(b) Monopoly

Under perfect competition, as uniform price prevails AR = MR and the demand curve (AR) is horizontal to X-axis.
A monopoly firm faces a downward-sloping demand curve.

Question 26.
Mention any two type of price discrimination?
Answer:

1. Personal
2. Geographical
3. On the basis of use.

Question 27.
Define “Excess capacity”.
Answer:

1. Excess capacity is the difference between the optimum output that can be produced and the actual output produced by the firm.
2. In the long run, a monopolistic firm produces deliberate output that is less than the optimum output that is the output corresponding to the minimum average cost.
3. This leads to excess capacity which is actually a waste in monopolistic competition.

Part – C

Answer the following questions in One Paragraph

Question 28.
What are the features of a market?
Answer:
A market has the following characteristic features:

1. Buyers and sellers of a commodity or a service.
2. A commodity to be bought and sold.
3. Price agreeable to buyer and seller.
4. Direct or indirect exchange.

Question 29.
Specify the nature of entry of competitors in perfect competition and monopoly.
Answer:
Nature of entry of competitors in perfect competition:

1. A large number of Buyers and Sellers.
2. Homogeneous Product and Uniform Price.
3. Free Entry and Exit.
4. Absence of Transport Cost.
5. Perfect Mobility of Factors of Production.
6. Perfect Knowledge of the Market.
7. No Government Intervention.

Nature of entry of competitors in Monopoly:

1. There is a single producer/seller of a product.
2. The product of a monopolist is unique and has no close substitute.
3. There is a strict barrier to entry of any new firm.
4. The monopolist is a price-maker.
5. The monopolist earns maximum profit / abnormal profit.

Question 30.
Describe the degree of price discrimination?
Answer:
Degrees of Price Discrimination:
Price discrimination has become widespread in almost all monopoly markets. According to A.C.Pigou, there are three degrees of price discrimination.

1. First degree price discrimination:
A monopolist charges the maximum price that a buyer is willing to pay. This is called as perfect price discrimination. This price wipes out the entire consumer’s surplus. This is maximum exploitation of consumers. Joan Robinson named it as “Perfect Discriminating Monopoly”.

2. Second degree price discrimination:
Under this degree, buyers are charged prices in such a way that a part of their consumer’s surplus is taken away by the sellers. This is called as imperfect price discrimination. Joan Robinson named it as “Imperfect Discriminating Monopoly”.

Under this degree, buyers are divided into different groups and a different price is charged for each group. For example, in cinema theatres, prices are charged for same film show from viewers of different classes. In a theatre the difference between the first row of first-class and the last row in the second class is smaller as compared to the differences in charges.

3. Third degree price discrimination:
The monopolist splits the entire market into a few sub-market and charges different price in each sub-market. The groups are divided on the basis of age, sex and location. For example, railways charge lower fares from senior citizens. Students get discounts in museums, and exhibitions.

Question 31.
State the meaning of selling cost with an example.
Answer:

Selling Cost:
1. Selling Cost is the discussion of “ Product differentiation”, we can infer that the producer under monopolistic competition has to incur expenses to popularize his brand. This expenditure involved in selling the product is called selling cost. According to Prof. Chamberlin, Selling cost is “The cost incurred in order to alter the position or shape of the demand curve for a product”.

2. Most important form of selling cost is an advertisement. Sales promotion by an advertisement is called non – price competition.

3. Product differentiation through effective advertisement is another method. This is known as sales promotion. Be frequently advertising the brand of the product through Press, Film, Radio, and TV. The consumers are made to feel that the brand produced by the firm in question is superior to that of other brands sold by other firms.

4. Product differentiation may also be affected by offering customers some benefits with the sale of the product. Facilities like free servicing, home delivery, acceptance of returned goods, etc.

Example: Most important form of selling cost is advertisement [This is known as sales promotion]. By frequently advertising the brand of the product through press, film, radio, T.V.

Question 32.
Mention the similarities between perfect competition and monopolistic competition,
Answer:

1. In both perfect competition and monopolistic competition number of firms are large.
2. Competition exists between the firms.
3. There are no barriers for entry and exit in both the markets.
4. Equilibrium occurs at the point where MC curve intersects MR curve.
5. In short run there is supernormal profit or loss and in long run there is only normal profits in both market structures.

Question 33.
Differentiate between ‘firm’ and ‘industry’.
Answer:
Firm :
A firm refers to a single production unit in an industry, producing a large or a small quantity of a commodity or service, and selling it at a price in the market. Its main objective is to earn a profit.

Industry :
An industry refers to a group of firms producing the same product or service in an economy.
(Eg.) A group of firms producing cement is called a cement industry.

Question 34.
State the features of duopoly.
Answer:

1. Each seller is fully aware of his rival’s motive and actions.
2. Both sellers may collude, (they agree on all matters regarding the sale of the commodity).
3. They may enter into cut-throat competition.
4. There is no perfect differentiation.
5. They fix the price for their product with a view to maximizing their profit.

Part – D

Answer the following questions in about a page

Question 35.
Bring out the features of perfect competition.
Answer:
Features of the perfect competition:
1. a Large Number of Buyers and sellers:

• “A large number of buyers” implies that each individual buyer buys a very, very small quantum of a product as compared to that found in the market.
• This means that he has no power to fix the price of the product.
• He is only a price-taker and not a price-maker
• A large number of sellers implies that the share of each individual seller is a very, very small quantum of a product.
• No power to fix the price of the product.

2. Homogeneous Product and Uniform Price:

• The product sold and bought is homogeneous in nature, in the sense that the units of the product are perfectly substitutable.
• All the units of the product are identical i.e., of the same size, shape, colour, quality, etc.
• Therefore, a uniform price prevails in the market.

3. Free Entry and Exit:

• In the short run, it is possible for the very efficient producer, producing the product at a very low cost, to earn supernormal profits.
• An inefficient producer, who is unable to bring down the cost incurs a loss.

4. Absence of Transport Cost:

• The prevalence of the uniform price is also due to the absence of the transport cost.

5. Perfect Mobility of Factors of Production:

• The prevalence of the uniform price is also due to the perfect mobility of the factors of production.
• As they enjoy perfect freedom to move from one place to another and from one occupation to another, the price gets adjusted.

6. Perfect Knowledge of the Market:

• All buyers and sellers have a thorough knowledge of the quality of the product, prevailing price, etc.

7. No Government Intervention:

• There is no government regulation on the supply of raw materials, and in the determination of price, etc.

Question 36.
How price and output are determined under the perfect competition?
Answer:
In the short run at least a few factors of production are fixed. The firms under perfect .competition take the price (10) from the industry and start adjusting their quantities produced.
For example
Qd = 100 -5P and
Qs = 5p
At equilibrium Qd = Qs
100 – 5p = 5p
100 = 5p + 5p
p = 10
Qd = 100 – 5(10)
= 50
Qs = 5(10) = 50
Qd = Qs
50 = 50

SS – market supply, DD – market demand, AR – Average Revenue, AC – Average Cost, MR – Marginal Revenue, MC – Marginal Cost This diagram consists of three panels.
First part:
The equilibrium of an industry is explained. The demand and supply forces of the firms interact and the price is fixed as Rs.10. The equilibrium of an industry is obtained at 50 units of output.

Second part:
AC curve is lower than the price line. Equilibrium is achieved where
MC = MR. Equilibrium quantity is 50. With price Rs. 10, it experiences supernormal profit
AC = Rs. 8
AR = Rs. 10
TR – 50 x 10 = 500
TC = 50 x 8 = 400
Profit = 500-400= 100.

Third part:
Firm’s cost curve is above the price line. Equilibrium MC = MR. Quantity is 50 with price Rs. 10, it experiences loss (AC > AR)
TR = 50 x 10 = 500
TC = 50 x 12 = 600
Loss = 600-500= 100
If profit prevails in the market, new firms emerge results in declining price and if loss occurs the existing loss making firm exits results in increasing price consequent upon the entry and exit of new firms into the industry, firms always earn ‘normal profit’ in the long run.

Price and output determination in long run :
Long run equilibrium of the firm is illustrated in the diagram. Under perfect competition, long run equilibrium is only at minimum point of LAC. At point E,
LMC = MR = AR = LAC

In the diagram AR = AC. Equilibrium is at point E where price is 8 and output is 500. At this point, the profit of the firm is only normal. Thus condition for the long-run equilibrium of the firm is
Price = AR = MR = Minimum AC

At equilibrium SAC > LAC. Hence in the long-run equilibrium price is lower and quantity is larger compared to the short-run equilibrium price and quantity.

Question 37.
Describe the features oligopoly.
Answer:

1. Few large firms: Very few big firms own the major control of the whole market by producing a major portion of the market demand.
2. Interdependence among firms: The price and quality decisions of a particular firm are dependent on the price and quality decisions of the rival firms.
3. Group behavior: The firms under oligopoly realize the importance of mutual co-operation.
4. Advertisement cost: The oligopolist could raise sales either by advertising or improving the quality of the product.
5. Nature of product: Perfect oligopoly means homogeneous products and imperfect oligopoly deals with heterogeneous products.
6. Price rigidity: It implies that prices ate difficult to be changed. The oligopolistic firms do not change their prices due to the fear of rival’s reaction.

Question 38.
Illustrate price and output determination under monopoly.
Answer:
Monopoly is a market structure characterized by a single seller, selling the unique product with the restriction for a new firm to enter the market.

Price and Output Determination under Monopoly :
Nature of cost and revenue curves :
A monopoly is a one-firm industry. Therefore, a monopolist firm faces a downward-sloping demand curve. Since AR falls, MR lies below the AR curve (MR < AR)
The monopolist will continue to sell his product as long as his MR > MC

Condition for equilibrium :
Monopolists attain equilibrium at the level of output when MC = MR.
From the diagram, till he sells 3 units output, MR is greater than MC, and when he exceeds this output level, MR is less than MC. At equilibrium where MR = MC, price (AR) is Rs. 88. To know the profit of monopolists at equilibrium output, the average revenue curves and the average cost curves are used at equilibrium Output 3
AR= 88
AC = 50
Profit per unit = 88-50
= 38
= (AR – AC) × Total output
= (88 – 50) × 3
= 38 × 3
= 114

Question 39.
Explain price and output determined under monopolistic competition with help of diagram.
Answer:
Monopolistic competition refers to a market situation where there are many firms selling a differentiated product.

Price and output determination :
Nature of cost and revenue curves :
The monopolistic firm sell large quantity at less price. So, it faces a downward-sloping demand curve. AR curve is fairly elastic. MR curve falls below AR. AC curve will be ‘U’ shaped.

Condition for equilibrium :
MC = MR, MC curve should cut MR from below. If MC is less than MR, the sellers will find it profitable to expand their output.

Short-run equilibrium :

Profit is maximised when MC = MR. From the diagram.
OM – Equilibrium output OP – Equilibrium price
TR – OMQP TC – OMRS
Profit = OMQP-OMRS
= PQRS
This is super normal profit under short-run.
A monopolistic competitive firm may also incur loss in the short-run.

As shown in the diagram, the AR and MR curves are fairly elastic.
At equilibrium output is OM , price is OP
TR – OMQP
TC-OMLK
Total loss = TR-TC
= OMQP – OMLK
= PQLK

Long-run equilibrium :
In the long run, AR curve is more elastic or flatter. Hence, the firms will only earn normal profit.

Samacheer Kalvi 11th Economics Market Structure and Pricing Additional Questions and Answers

Part -A

Choose the best options

Question 1.
In the real world what type of market we see?
(a) Imperfect
(b) Perfect
(c) Monopoly
(d) Oligopoly
Answer:
(a) Imperfect

Question 2.
First condition for equilibrium of the firm _______
(a) AC = AR
(b) AC = MC
(c) MC = MR
(d) AR = MR
Answer:
(c) MC = MR

Question 3.
How many types of price discrimination under monopoly?
(a) Three
(b) Two
(c) Five
(d) Seven
Answer:
(a) Three

Question 4.
Indian railways is an example of _______ competition.
(a) Perfect competition
(b) Monopoly
(c) Monopolistic competition
(d) Oligopoly
Answer:
(b) Monopoly

Question 5.
Monopoly power achieved through patent right is called ………………………..
(a) Duopoly
(b) Oligopoly
(c) Legal monopoly
(d) Monopolistic competition
Answer:
(c) Legal monopoly

Question 6.
Differentiated products are seen in _______
(a) Perfect competition
(b) Monopoly
(c) Monopolistic
(d) Monopsony
Answer:
(c) Monopolistic

Question 7.
Under perfect competition, the firms are producing …………………………
(a) Firm
(b) Sales
(c) Public sector
(d) Homogeneous
Answer:
(d) Homogeneous

Question 8.
In perfect competition, short run equilibrium is determined by
(a) MC = MR
(b) MC = AC
(c) MR = AR
(d) AR = AC
Answer:
(a) MC = MR

Question 9.
A firm and Industry are one and the same under ……………………
(a) Perfect competition
(b) Duopoly
(c) Oligopoly
(d) Monopoly
Answer:
(d) Monopoly

Question 10.
Group behaviour is seen in _______
(a) Perfect competition
(b) Monopoly
(c) Monopolistic competition
(d) Oligopoly
Answer:
(d) Oligopoly

Question 11.
When the monopoly will be an equilibrium?
(a) MC = MR
(b) AC = AR
(c) AC = MR
(d) MC = AR
Answer:
(a) MC = MR

Question 12.
_______ degree of price discrimination wipes out the entire consumer’s surplus.
(a) First
(b) Second
(c) Third
(d) None
Answer:
(a) First

Question 13.
In monopolistic competition, the demand curve is
(a) More elastic
(b) Inelastic
(c) Less elastic
(d) None
Answer:
(a) More elastic

Question 14.
Government controls monopoly by _______
(a) Taxation
(b) Legal methods
(c) Both
(d) None
Answer:
(c) Both

Question 15.
The important feature of non-price competition is _______
(a) Product differentiation
(b) Advertisement
(c) Sales promotion
(d) All the above
Answer:
(d) All the above

Question 16.
The concept of Imperfect Competition was
(a) J.M. Keynes
(b) Irving Fisher
(c) Marshall propounded by
(d) Joan Robinson
Answer:
(d) Joan Robinson

Question 17.
Identify the wrong statement about the features of Duopoly.
(a) There is product differentiation
(b) They fix the price for their product to maximise their profit
(c) Each seller is fully aware of his rival’s motive and actions
(d) Both sellers may collude regarding the sale of commodity.
Answer:
(a) There is product differentiation

Match the following and choose the answer using the codes given below

Question 1.

(a) 1 2 3 4
(b) 2 4 1 3
(c) 4 3 2 1
(d) 3 4 1 2
Answer:
(b) 2 4 1 3

Question 2.

(a) 2 4 1 3
(b) 3 1 4 2
(c) 3 4 1 2
(d) 1 2 3 4
Answer:
(d) 1 2 3 4

Choose the incorrect pair

Question 3.

Answer:
(d) Sub-market (iv) Fourth degree price discrimination

Question 4.

Answer:
(b) Artificial monopoly (ii) Gold mines (Africa)

Choose the odd one out

Question 5.
(a) Personal
(b) Geographical
(c) On the basis of use
(d) Price taker
Answer:
(c) On the basis of use

Question 6.
(a) Individual behaviour
(b) Few large firms
(c) Group behaviour
(d) Price rigidity
Answer:
(a) Individual behaviour

Question 7.
(a) Market period
(b) Short period market
(c) Very long period market
(d) Whole sale market
Answer:
(d) Whole sale market

Choose the incorrect statement

Question 8.
In perfect competition
(a) There are large number of buyers and sellers
(b) Free entry and exit of firm
(c) Price competition is essential
(d) Independent price policy
Answer:
(c) Price competition is essential

Question 9.
(a) In a market there is no exchange of goods.
(b) Commodities will be bought and sold in market.
(c) In market prices are agreeable to buyer and seller.
(d) In market there are buyer and seller of a commodity.
Answer:
(a) In a market there is no exchange of goods.

Analyse the reason for the following 

Question 10.
Assertion (A) : Perfect competition is that no one is big enough to have any appreciable
influence over market price.
Reason (R) : Perfect competition is a market situation where there are infinite number of sellers.
(a) Both (A) and (R) are true, (R) is the correct explanation of (A)
(b) Both (A) and (R) are true, (R) is not the correct explanation of (A)
(c) Both (A) and (R) are false.
(d) (A) is true but (R) is false.
Answer:
(a) Both (A) and (R) are true, (R) is the correct explanation of (A)

Question 11.
Assertion (A) : At equilibrium MC cuts MR from below.
Reason (R) : MC cuts MR at two points.
(a) Both (A) and (R) are true, (R) is the correct explanation of (A)
(b) Both (A) and (R) are true, (R) is not the correct explanation of (A)
(c) (A) is true but (R) is false.
(d) (A) is false but (R) is true.
Answer:
(b) Both (A) and (R) are true, (R) is not the correct explanation of (A)

Question 12.
Assertion (A) : In monopoly there exist price discrimination.
Reason (R) : A monopolist is a price maker.
(a) Both (A) and (R) are true, (R) is the correct explanation of (A)
(b) Both (A) and (R) are false
(c) (A) is true but (R) is false.
(d) (A) is false but (R) is true.
Answer:
(a) Both (A) and (R) are true, (R) is the correct explanation of (A)

Choose the incorrect pair 

Question 13.

Answer:
(c) Monopolistic competition (iii) Non – price discrimination

Question 14.

Answer:
(b) Oligopoly (ii) Group behaviour

Fill in the blanks with suitable option given below 

Question 15.
Supply curve in the very short period is ________
(a) Horizontal
(b) Slopes downward
(c) Slopes upward
(d) Vertical
Answer:
(d) Vertical

Question 16.
Differentiated products are seen in ________
(a) Perfect competition
(b) Monopoly
(c) Monopolistic competition
(d) Monopsony
Answer:
(c) Monopolistic competition

Question 17.
Government controls monopoly by ________
(a) Taxation
(b) Legal method
(c) Both
(d) None
Answer:
(c) Both

Choose the best option 

Question 18.
________ classified market based on time
(a) Marshall
(b) Adam smith
(c) Chamberlin
(d) Hicks
Answer:
(a) Marshall

Question 19.
In monopolistic competition the demand curve is
(a) Inelastic
(b) More elastic
(c) Less elastic
(d) None
Answer:
(b) More elastic

Question 20.
The important feature of non-price competition is ________
(a) Product differentiation
(b) Advertisement
(c) Sales promotion
(d) All the above
Answer:
(d) All the above

Part – B

Answer the following questions in one or two sentences

Question 1.
Define duopoly?
Answer:
In a duopoly, there are only two sellers who are completely independent and no agreement exists between them.

Question 2.
Define “ Imperfect competition”?
Answer:
Imperfect competition is a competitive market situation where there are many sellers, but they are selling heterogeneous (dissimilar) goods as opposed to the perfect competitive market scenario. As the name suggests, competitive markets are imperfect in nature.

Question 3.
Classify market based on time.
Answer:

1. Very short period market (or) Market period.
2. Short period market
3. Long period market
4. Very long period market (or) Secular period market.

Question 4.
How is market classified based on the quantify of a commodity?
Answer:

1. Whole-sale market
2. Retail market

Question 5.
How can you classify market-based on the competition?
Answer:

1. Perfect competition market.
2. Imperfect competition market which comprises monopoly, monopolistic competition, duopoly, oligopoly etc.

Question 6.
Define long-run average cost curve.
Answer:
In the long run all the factors are variable. The LAC curve is an envelope curve as it contains a few average cost curves. It is a flatter ‘U’ shaped one. It is also called as planning curve.

Question 7.
Write a note imperfect competition.
Answer:
This concept was introduced by Joan Robinson and E.H.Chamberlin. Imperfect competition is a competitive market situation where there are many sellers, but they are selling heterogeneous goods. Competitive markets are imperfect in nature.

Question 8.
Explain monopoly.
Answer:
‘Mono’ refers to a single and ‘poly’ to seller. In this way, monopoly refers to a market situation in which there is only one seller of a commodity. There is no scope for competition.

Question 9.
What is dumping?
Answer:
Dumping refers to practice of the monopolist charging higher price for his product in the local market and lower price in the foreign market. It is called as ‘International price discrimination’.

Question 10.
What is monopsony?
Answer:
Monopsony is a market structure in which there is only one buyer of a good or service.

Question 11.
What is a Bilateral monopoly?
Answer:
If a single producer of a product faces a single buyer of that product, then it is called as bilateral monopoly.

Question 12.
What are the conditions for short, run and long-run equilibrium in the monopolistic competition ?
Answer:
Short – run equilibrium : MC = MR
Long – run equilibrium has two conditions : MC = MR and AC = AR

Question 13.
Give example for perfect competition.
Answer:

1. Online ticket auctions.
2. Truck farming
3. Salt
4. Gravel
5. Garage sales
6. Online sales in general

Question 14.
What is oligopoly?
Answer:
Oligopoly is a market situation in which there are a few firms selling homogeneous or differentiated products.

Part – C

Answer the following questions in One Paragraph

Question 1.
Explain the types of markets based on area.
Answer:
The market is classified not only on its geographical spread but also on the nature of the goods exchanged.
1. Local market:
It refers to the products or services which are sold and bought in the place of their production. (Eg.) Fruits, Vegetables etc.

2. Provincial market:
It arises when products or services are sold and bought in a restricted circle. (Eg.) : Provincial newspaper.

3. National market:
It arises when products and services are sold and bought throughout a country. (Eg.) Tea, Coffee, Cement etc.

4. International market:
It arises when products and services are sold and bought at the world level. (Eg.) Petrol, Gold etc.

Question 2.
What are the Duopoly and the characteristics of Duopoly?
Answer:
Duopoly is a special case of the theory of oligopoly in which there are only two sellers. Both the sellers are completely independent and no agreement exists between them. Even though they are independent, a change in the price and output of one will affect the other, and may set a chain of reactions. A seller may, however, assume that his rival is unaffected by what he does, in that case he takes only his own direct influence on the price.

Characteristics of Duopoly:

1. Each seller is fully aware of his rival’s motive and actions.
2. Both sellers may collude (they agree on all matters regarding the sale of the commodity).
3. They may enter into cut-throat competition.
4. There is no product differentiation.
5. They fix the price for their product with a view to maximizing their profit.
6. Describe the features of monopolistic competition.

Features of monopolistic competition:

1. There are a large number of buyers and many sellers.
2. Firms under monopolistic competition are price makers. They set their own prices.
3. Firms produce differentiated products. It is the key element of monopolistic competition.
4. There is a free entry and exit of firms.
5. Firms compete with each other by incurring selling cost or expenditures on sales promotion of their products.
6. Non – price competition is an essential part of monopolistic competition.
7. A firm can follow an independent price policy.

Question 3.
Classify markets based on quantity of the commodity.
Answer:
1. Whole-sale market:
It is for bulk selling and buying of goods. The price is likely to be low compared to the retail market. (Eg.) Clothing, Grocery etc.

2. Retail market:
It is the market for commodities in small quantities .(Eg.) Clothing, Vegetable, etc.

Question 4.
Explain the total cost curve approach.
Answer:
In the TC – TR approach, profit is obtained by a firm, through the difference between the TC and the TR.
Equilibrium is obtained at the point where the maximum difference between the TC and TR occurs.

Question 5.
State the two conditions for equilibrium using the marginal curve approach.
Answer:

1. MC = MR
A rational seller will not be in equilibrium at output level 1, though MC = MR at that point. He continues his production till 5 units where MC < MR. Beyond 5 units of Q, MC > MR where the seller incurs loss. So condition for equilibrium MC – MR. It is a necessary but not a sufficient condition.

2. MC cuts MR curve from below (Sufficient conditions):
MC curve is ‘U’ shaped. MR cuts MC both from above (at point A) and also from below (at point B). Only at point B the equilibrium condition is fulfilled.

Thus for equilibrium under all market situations the two conditions are MC = MR and MC cuts MR from below.

Question 6.
Explain the features of monopoly.
Answer:

1. There is a single producer/seller of a product.
2. The product of a monopolist is unique and has no close substitute. There is a strict barrier to entry of any new firm.
3. The monopolist is a price – maker.
4. The monopolist earns maximum profit / abnormal profit.

Question 7.
Explain the sources of monopoly power.
Answer:
1. Natural monopoly :
Ownership of the natural raw materials. (Eg.) Gold mines (Africa)

2. State monopoly :
Single supplier of some special services. (Eg.) Railways in India

3. Legal monopoly :
A monopoly firm can get its monopoly power by getting patent rights, trade mark from
the government.

Question 8.
Explain the features of monopolistic competition.
Answer:

1. There are a large number of buyers and sellers.
2. Firms under monopolistic competition are price makers.
3. They produce differentiated products.
4. There is a free entry and exit of firms.
5. Finns compete with each other by incurring selling costs or expenditure on sales promotion.
6. Non-price competition is an essential part of monopolistic competition.
7. A firm can follow an independent price policy.

Question 9.
Explain the types of price discrimination.
Answer:
1. Personal :
Different prices are charged for different individuals.
(Eg.) Tickets at a concessional rate to the senior citizens in railways.

2. Geographical:
Different prices are charged at different places for the same product.
(Eg.) A book sold within India at a price is sold in a foreign country at a lower price.

3. On the basis of use :
Different prices are charged according to the use of a product.
(Eg.) TNEB charges lower rate for domestic use of electricity and higher rate for commercial uses.

Part – D

Answer the following questions in about a page

Question 1.
Explain long-run equilibrium in perfect competition.
Answer:
In the long run, all the factors are variable.
The LAC curve is an envelope curve as it contains a few average cost curves.
It is a flatter ‘U’ shaped one. It is also known as the planning curve.

1. The firms will earn an only normal profit.
2. All the firms in the market are in equilibrium. So entry and exit of a firm is not possible.
   

A firm under perfect competition, in the long run, is a price-taker. It takes the price of the product from the industry. And it superimposes its cost curves on the revenue curves.

Long-run equilibrium is at the minimum point of LAC. In the diagram AC = AR, at equilibrium E price is 8 and output is 500. At this point, the profit of the firm is only normal.

The condition for the long-run equilibrium of the price is.
Price = AR = MR = Minimum AC. At this equilibrium.

1. SAC > LAC
2. Long run equilibrium price is lower than the short-run equilibrium price.
3. Long run equilibrium quantity is larger than short-run equilibrium quantity.

Question 2.
Describe the wastes of monopolistic competition?
Answer:
Wastes of Monopolistic Competition:
Generally there are five kinds of wastages under monopolistic competition.
1. Excess capacity:

• Un-utilized capacity is the difference between the optimum output that can be produced and the actual output produced by the firm.
• In the long run, a monopolistic firm produces delibourately output which is less than the optimum output that is the output corresponding to the minimum average cost.
• This leads to excess capacity which is actually as waste in monopolistic competition.

2. Unemployment:

• Under monopolistic competition, the firms produce less than optimum output.
• As a result, the productive capacity is not used to the fullest extent.
• This will lead to unemployment of human resources also.

3. Advertisement:

• There is a lot of waste in competitive advertisements under monopolistic competition.
• The wasteful and competitive advertisements lead to high cost to consumers.

4. Too many varieties of Goods:

• The goods differ in size, shape, style and colour. A reasonable number of varieties would be sufficient.

5. Inefficient firms:
Under monopolistic competition, inefficient firms charge prices higher than their marginal cost. Efficient firms cannot drive out inefficient firms.

Question 3.
Explain long-run equilibrium in perfect competition.
Answer:
Similarities :

1. The motive of both the type of market is profit maximisation.
2. Condition for equilibrium is MC = MR

Dissimilarities :

Perfect Competition:

1. Price taker. As the contribution of a single seller is less he cannot determine the price
2. At equilibrium MC = MR = AR (Price)
3. AR curve is perfectly elastic and horizontal to X-axis. MR curve is equal to AR and coincides with AR. AR = MR
4. Equilibrium is attained at increasing marginal cost conditions.
5. In the short – run the firm earns super normal profit. In the long run, attracted by super-normal profit new firms enter the industry, which results in normal profit.
6. The firms produce optimum quantity of output.
7. Price discrimination is not possible, because of the perfectly elastic demand curve.
8. Output is maximum and price is minimum.
9. Possibility for consumer’s surplus.

Monopoly:

1. Price maker. As the firm and industry remains the same, producer fix price for his product.
2. At equilibrium MC = MR < AR (Price)
3. AR curve is a downward-sloping curve. MR falls below AR.
4. Equilibrium can be attained during increasing, decreasing and constant marginal cost conditions.
5. In both short-run and long-run the firm earns super-normal profit because of the barrier to entry.
6. The firm produces less than the optimum quantity of output.
7. Price discrimination is possible.
8. Output is minimum and price is maximum.
9. As the price is high there is no possibility for a consumer’s surplus.

Question 4.
Explain long-run equilibrium of the firm and the group equilibrium in monopolistic competition.
Answer:
In the short run, the firm may earn super normal profit or incur loss. But in the long run, the entry of the new firms in the industry will wipe out the super normal profit earned by the existing firms. The entry of new firms and exit of loss making firms will result in normal profit for the firms in the industry.

In the long run AR curve is more elastic or flatter. Because plenty of substitutes are available.

In the diagram, equilibrium is achieved at point E The equilibrium output is ‘OM’ and the equilibrium price is ‘OP’. AR is ‘MQ’ and MC is also ‘MQ’.

In the long run, the condition for equilibrium is AR = AC And MC = MR. It means that a firm earns a normal profit. AR is tangent to the Long-run Average Cost (LAC) curve at point ‘Q’.

Students can Download Commerce Chapter 31 Discharge and Breach of a Contract Questions and Answers, Notes Pdf, Samacheer Kalvi 11th Commerce Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Samacheer Kalvi 11th Commerce Solutions Chapter 31 Discharge and Breach of a Contract

Samacheer Kalvi 11th Commerce Discharge and Breach of a Contract Textbook Exercise Questions and Answers

I. Choose the Correct Answer

Question 1.
On the valid performance of the contractual obligation by the parties, the contract ……………….
(a) Is discharged
(b) Becomes enforceable
(c) Becomes void
(d) None of these
Answer:
(a) Is discharged

Question 2.
An agreement to do an act impossible in itself under Section 56 is ……………….
(a) Void
(b) Valid
(c) Voidable
(d) Unenforceable
Answer:
(a) Void

Question 3.
Any agreement which becomes impossible to perform under various circumstances.
(a) Voidable
(b) Void
(c) Valid
(d) None of these
Answer:
(b) Void

Question 4.
Discharge by mutual agreement may involve ……………….
(a) Novation
(b) Rescission
(c) Alteration
(d) All of the above
Answer:
(d) All of the above

Question 5.
The compensation given for breach of contract is ……………….
(a) Damage
(b) Remuneration
(c) Money
(d) Cheque
Answer:
(a) Damage

II. Very Short Answer Questions

Question 1.
What are the kinds of consent?
Answer:
Consent can be classified into four types, namely; Implied Consent, Expressed consent, Informed Consent, and Unanimous consent.

Question 2.
What are the types of Impossibility of Performance?
Answer:
There are two types of the impossibility of performance, such as –

1. Impossibility existing at the time of the agreement.
2. Impossibility arising subsequent to the formation of the contract.

Question 3.
What is Quantum merit?
Answer:
The meaning of the phrase quantum merit is ‘as much as earned’. It has been arising if a contract performed by one party has become discharged by breach of the other party. The claim is not for the original contract that has been discharged or void, but on an implied promise by the other party to pay for what he has done.

III. Short Answer Questions

Question 1.
What are the different modes of discharge by implied consent?
Answer:
Different modes of discharge by implied consent are:

1. Novation
2. Alteration
3. Recession
4. Remission
5. Accord and Satisfaction
6. Waiver
7. Merger

Question 2.
Define discharge by Performance.
Answer:
Performance implies carrying out the obligation of the contract. Performance must be completed according to the real intentions of the agreement. Performance must be done according to the time and manner prescribed. Performance of contract may be of two types namely

1. Actual performance
2. Attempted performance.

Question 3.
What are the reasons for impossibility arising after the formation of a contract?
Answer:
Impossibility arising subsequent to the formation of a contract or supervening impossibility may be:

1. By some event beyond the control of the parties; or
2. By some act either of the promisor or of the promisee.

Question 4.
What are the various rules regarding damages?
Answer:
Damages are monetary compensation awarded by the court to the injured party for the loss or injury suffered by him. The following are the rules regarding damages

• As per the contract, one party can claim damages if the other parties breach the contract.
• The main purpose of awarding the damages is to make good the loss suffered by him. It is known as the doctrine of restitution.
• Section 73 of the Indian Contract Act, 1872 deals with the compensation for loss or damages caused by a party for breach of contract.

IV. Long Answer Questions

Question 1.
Explain the ways of discharge of Contract?
Answer:
Different modes of discharge of contract have been provided under different sections of the Act:
1. Discharge by Performance: Performance implies carrying out the obligation of the contract. Performance must be completed according to the real intentions of the agreement. Performance must be done according to time and manner prescribed. Performance of contract may be of two types namely:

• Actual performance
• Attempted performance

2. By Agreement on Consent: Agreement between the parties comes to an end by mutually agreeing for it. Any contract is created by an agreement, hence in the same way, it can be discharged by an agreement. The consent may be of the following types:

• Express consent
• Implied consent

3. By Impossibility of Performance: A contract may be discharged if its performance becomes impossible. There are two types of the impossibility of performance, such as –

• Impossibility existing at the time of the agreement.
• Impossibility arising subsequent to the formation of the contract.

4. By Lapse of Time: According to the Limitation Act, 1963 a contract must be performed within a specified time. If it is not performed within this specified time limit and against which if no action is taken by the promisee in the Court of Law within a specified time, then the promisee is deprived of his remedy at law. In such cases, the contract is discharged.

5. By Operation of Law: A contract can be discharged by the operation of law. The operation of law by which contract can be discharged are as follows:

• By Death
• By Merger
• By Insolvency
• Unauthorized Alteration of the Terms of a Contract
• Rights and liabilities vesting in the same person

Question 2.
Write about the various remedies for breach of contract.
Answer:
All parties to a contract are expected to perform their promises. When one party refuses to perform his promise, then the breach of contract takes place. The other party or parties are called aggrieved or injured party or parties. There are various types of remedies for the injured parties listed as follows:
The recession of Contract:
In case of breach of contract by one party, then the other parties may rescind the contract and thereby the party is absolved from all obligations under the contract.

Claim for Specific Performance:
In some specific cases if the damages are not an adequate remedy, then the court can direct the party in breach for the specific performance of the contract. In such a case, the promise is carried out as per the terms and conditions of the contract.

Claim for Injunction:
The injunction is an order passed by a competent court restraining a person from doing some act. An injunction can be defined as a mode of securing the specific performance of the negative terms of a contract. Negative terms of contract imply doing something, which a party has promised not to do. The injunction is an order which is granted by the court restraining the person to do what he had promised not to do.

Claim for Quantum Merit:
The claim for quantum merit may arise if a contract performed by one party has become
discharged by breach of the other party. The meaning of the phrase quantum merit is ‘as much as earned’. The claim is not for the original contract that has been discharged or void, but on an implied promise by the other party to pay for what he has done.

Claim for damages:
Damages are monetary compensation awarded by the court to the injured party for the loss or injury suffered by him. As per the contract, one party can claim damages if other parties breach the contract. The main purpose of awarding the damages is to make good the loss suffered by him. It is known as the doctrine of restitution. Section 73 of the Indian Contract Act, 1872 deals with the compensation for loss or damages caused by a party for breach of contract.

Question 3.
Discuss the different types of damages awarded to the injured party.
Answer:
The following are the different types of damages awarded to the injured party:
1. Ordinary damages:
The damages which arise in the ordinary course of events from the breach of contract are called ordinary damages. These damages constitute the direct loss suffered by the aggrieved party.

2. Special Damages:
Special damages are those damages that are payable for the loss arising on account of some special or unusual circumstances. They are not due to the natural and probable consequences of the breach of the contract. Special damages can be recovered only when the other party while signing the contract, is informed of the special circumstances which are responsible for the special losses.

3. Exemplary or Vindictive Damages:
These damages are awarded against the party who has committed a breach of the contract with the object of punishing the erring as defaulting party and compensating the aggrieved party. These damages are awarded in the case of action on lost or breach of promise.

4. Nominal damages:
Nominal damages are awarded to the aggrieved party when there is only a technical violation of the legal rights. Here no substantial loss is caused. These damages are very small in amount. They are awarded simply to recognize the right of the party to claim damages for the breach of the contract.

Students can Download Chemistry Chapter 12 Basic Concepts of Organic Reactions Chemistry Questions and Answers, Notes Pdf, Samacheer Kalvi 11th Chemistry Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Chemistry Solutions Chapter 12 Basic Concepts of Organic Reactions

Samacheer Kalvi 11th Chemistry Basic Concepts of Organic Reactions Textual Evaluation Solved

I. Choose The Best Answer:

Question 1.
For the Following reactions –
(A) CH₃ CH₂ CH₂ Br + KOH → CH₃ – CH + KBr + H₂O
(B) (CH₃ )₃ CBr + KOH → (CH₃ )₃ COH + KBr
(C)
Which of the following statement is correct’?
(a) (A) is elimination, (B) and (C) are substitution
(b) (A) is substitution, (B) and (C) are elimination
(c) (A) and (B) are elimination and (C) is addition reaction
(d) (A) is elimination, B is substitution and (C) is addition reaction.
Answer:
(d) (A) is elimination, B is substitution and (C) is addition reaction.

Question 2.
What is the hybridisation state of benzyl carbonium ion?
(a) sp²
(b) spd²
(c) sp³
(d) sp²d
Answer:
(a) sp²

Question 3.
Decreasing order of nucleophilicity is –
(a) OH^–> RNH₂^– > ^–OCH₃> RNH₂
(b) NH₂^–> OH^–> ^–OCH₃> RNH₂
(c) NH,> CH₃O >OH^–> RNH₂
(d) CH₃O^–> NH₂^–> OH^–> RNH₂
Answer:
(b) NH₂^–> OH^–> ^–OCH₃> RNH₂₊

Question 4.
Which of the tòllowing species is not eLectrophilic in nature?
(a) Cl⁺
(b) BH₃
(c) H₃O⁺
(d) ⁺NO₂
Answer:
(c) H₃O⁺

Question 5.
Homolytic fission of covalent bond leads to the formation of –
(a) electrophile
(b) nucicophile
(c) Carbocation
(d) free radical
Answer:
(d) free radical

Question 6.
Hyper Conjugation is also known as –
(a) no bond resonance
(b) Baker – nathan effect
(c) both (a) and (b)
(d) none of these
Answer:
(c) both (a) and (b)

Question 7.
Which of the group has highest +I effect?
(a) CH₃^–
(b) CH₃CH₂^–
(c) (CH₃)₂ -CH-
(d) (CH₃)₃-C-
Answer:
(d) (CH₃)₃-C-

Question 8.
Which of the following species does not exert a resonance effect?
(a) C₆H₅OH
(b) C₆H₅Cl
(c) C₆H₅NH₂
(d) C₆H₅NH₃
Answer:
(d) C₆H₅NH₃

Question 9.
-I effect is shown by –
(a) -Cl
(b) -Br
(c) both (a) and (b)
(d) -CH₃
Answer:
(c) both (a) and (b)

Question 10.
Which of the following carbocation will be most stable?
(a) \({ PH }_{ 3 }\overset { + }{ C- } \)
(b) CH₃–\(\overset { + }{ C{ H }_{ 2 } } \)
(c) (CH₃)₂–\(\overset { + }{ C{ H } } \)
(d) CH₂ = CH-CH₃
Answer:
(a) \({ PH }_{ 3 }\overset { + }{ C- } \)

Question 11.
Assertion : Tertiary Carbocations are generally formed more easily than primary Carbocations.
Reason : Hyper conjugation as well as inductive effect due to additional alkyl group stabilize tertiary carbonium ions.
(a) both assertion and reason arc true and reason is the correct explanation of assertion.
(b) both assertion and reason are true but reason is not the correct explanation of assertion.
(c) Assertion is true but reason is false
(d) Both assertion and reason are false
Answer:
(a) both assertion and reason are true and reason is the correct explanation of assertion.

Question 12.
Heterolytic fission of C-C bond results in the formation of –
(a) free radical
(b) Carbanion
(c) Carbocation
(d) Carbanion and Carbocation
Answer:
(e) Carbocation

Question 13.
Which of the following represent a set of nucleophiles?
(a) BF₃, H₂O, NH^2-
(b) AlCl₃, BF₃, NH₃
(c) CN^–, RCH^–₂, ROH
(d) H⁺, RNH⁺₂, CCl₂
Answer:
(c) CN^–, RCH^–₂, ROH

Question 14.
Which of the following species does not acts as a nucleophile?
(a) ROH
(b) ROR
(c) PCl₃
(d) BF₃
Answer:
(d) BF₃

Question 15.
The geometrical shape of carbocation is
(a) Linear
(b) tetrahedral
(c) Planar
(d) Pyramidal
Answer:
(c) Planar

II. Write brief answer to the following questions.

Question 16.
Write short notes on:
(a) Resonance
(b) Hyper conjugation
Answer:
(a) Resonance:
1. Certain organic compounds can be represented by more than one structure and they differ only in the position of bonding and lone pair of electrons. Such structures are called resonance structure and this phenomenon is called as resonance. This phenomenon is also called as mesomerism or mesomeric effect.

2. For example, the structure of aromatic compounds such as benzene and conjugated system like 1,3 butadiene cannot be represent by a single structure and their observed properties can be explained on the base of a resonance hybrid.

3. Resonance structure of benzene.

(I) and (II) are called as resonance hybridš of benzcnc.

4. For 1,3 butadiene:

(I), (II) and (III) are called as resonance hybrids of 1,3 butadiene.

(b) Hyper conjugation:
1. The denationalization of electrons of σ bond is called as hyper conjugation. it is a special stabilizing effect that results due to the interaction of electrons of a σ bond with the adjacent empty non-bonding P-orbitais resulting in an extended molecular orbital.

2. Hyper conjugation is a permanent effect.

3. For example, in propane. the σ- electrons of C-H bond of methyl group can be delocalised into the it- orbital of doubly bonded carbon as represented below.

Question 17.
What are electrophiles and nucleophiles? Give suitable examples for each.
Answer:
Nucleophiles are reagents that has high affinity for electron positive centers. They possess an atom that has an unshared pair of electrons, and hence it is in search for an electro-positive centre where it can have an opportunity to share its electrons to form a covalent bond, and gets stabilised. They are usually negatively charged ions or electron-rich neutral molecules (contains one or more lone pair of electrons). All Lewis bases act as nucleophiles.
Example :
Ammonia(NH₃) and amines (RNH₂), water (H₂O), alcohols (ROH) and ethers ((R-O-R)

Electrophiles:
Electrophiles are reagents that are attracted towards negative charge or electron-rich center. They are either positively charged ions or electron-deficient neutral molecules. All Lewis acids acts as electrophiles. Neutral molecules like SnCl4 can also act as an electrophile, as it has vacant d – orbitals which can accommodate the electrons from others.
Example:
Carbon dioxide (CO₂), dichlorocarbene (: CCl₂), Aluminium chloride (AlCl₃), boron trifluoride (BF₃) and Ferric Chloride (FeCl₃)

Question 18.
Show the heterolysis of the covalent bond by using curved arrow notation and complete the following equations. Identify the nucleophile In each case.
1. CH₃-Br+KOH →
2. CH₃-OCH₃+HI →
Answer:

In this case, \(\overset { \ominus }{ Br } \) and \(\overset { \ominus }{ OH } \) are nucleophiles.

Another mechanism:
Step – I

Step-II

In this case, OCH₃ and -I are nucleophiles
Another mechanism:
Step – I

Step – II

Question 19.
Explain inductive effect with suitable example.
Inductive effect:
Answer:
1. it is defined as the change ¡n the polarization of a covalent bond due to the presence of adjacent bonded atoms or groups in the molecule. It is denoted as I-effect.

2. Atoms or groups which lose electron towards a carbon atom are said to have a +I effect.
Example:
CH₃-,(CH₃)₂ CH-,(CH₃)₂ C- etc.

3. Atoms or groups which draw electrons away from a carbon atom are said to have a -I effect.
Example:
-NO₂. -I, -Br, -OH, C₆H₅ etc.

4. For example, consider ethane and ethyl chloride. The C-C bond in ethane is non polar while the C-C bond in ethyl chloride is polar. We know that chlorine is more electronegative than carbon and hence it attracts the shared pair of electrons between C-Cl in ethyl chloride towards it self.

This develops a slight negative charge on chlorine and a slight positive charge on carbon to which chlorine is attached. To compensate it, the C₁ draws the shared pair of electron between itself and C₂. This polarization effect is called inductive effect.

Question 20.
Explain the electromeric effect.
Electromeric effect:
Answer:
1. The electromeric effect refers to the polarity produced in a multiple bonded compound when it is attacked by a reagent when a double or a triple bond is exposed to an attack by an electrophile the two π electrons which from the π bond are completely transferred to one atom or the other.

2. When a nucleophile approaches the carbonyl compound, the π-electrons between C and O is instantaneously shifted to the more electronegative oxygen. This makes the carbon electron-deficient and thus facilitating the formation of a new bond between the incoming nucleophile and the carbonyl carbon atom.

3. When an electrophile such as H approaches an alkene molecule their electrons are instantaneously shifted to the electrophile and a new bond is formed between carbon and hydrogen. This makes the other carbon electron-deficient and hence it acquires a positive charge.

4. This effect denotes as E-effect.

Question 21.
Give examples for the following types of organic reactions
1. – elimination
2. Electrophilic substitution.
Answer:
1. β-elimination:
Elimination reactions involve the cleavage of a bond and tórmation of an air bond. A nucleophilic pair of electrons heads into a new it bond as a leaving group departs. This process is called 3-elimination because the bond Í to the nucleophilic pair of electrons breaks.
Example:
(a) n-propyl bromide on reaction with alcoholic KOH give propene. in this reaction hydrogen and Br are eliminated.

(b) Acid-catalysed dehydration of alcohols

2. Electrophilic substitution:
Substitution reactions when are brought about by electrophiles are called electrophilic substitution reaction.
Example:
(a) Nitration of benzene

(b) Bromination of benzene:

Samacheer Kalvi 11th Chemistry Basic Concepts of Organic ReactionsAdditional Questions Solved

I. Choose The Correct Answer.

Question 1.
Statement-I: All the organic molecules contain covalent bonds.
Statement-II: Organic molecules are formed by the mutual sharing of electrons between atoms.
(a) Statement-I and II are correct and statement-II is the correct explanation of statement-I.
(b) Statement-I and II are correct but Statement-II is not the correct explanation of statement-I.
(c) Statement-I is correct but statement-II is wrong.
(d) Statement-I is wrong but statement-II is correct.
Answer:
(a) Statement-I and II are correct and statement-II is correct explanation of statement-I.

Question 2.
Statement-I: Homolytic cleavage is an asymmetrical one.
Statement-II: A single covalent bond breaks and each of the bonded atoms retains one electron.
(a) Statement-I and II are correct and statement-II is correct explanation of statement-I.
(b) Statement-I and II are correct but statement-II is not correct explanation of statement-I.
(c) Statement-I is correct but statement-II is wrong.
(d) Statement-I is wrong but statement-II is correct.
Answer:
(a) Statement-I and II are correct and statement-Il is correct explanation of statement-I.

Question 3.
Heterolysis of propane gives
a) Methyl and ethyl free radicals
b) Methyl carbocation and ethyl free radicals
c) Methyl anion and ethyl carbocation
d) Methyl free radical and ethyl carbocation
Answer:
c) Methyl anion and ethyl carbocation

Question 4.
Which one of the following ¡s correct order of stability of alkyl free radicals?

Answer:

Question 5.
Statement-I: Ileterolytic cleavage is unsymmetrical one.
Statement-II: A covalent bond breaks and one of the bonded atom retains the bond pair of electrons.
(a) Statement-I and II are correct and statement-II is correct explanation of statement-I.
(b) Statement-I and II are correct but statement-II is not correct explanation of statement-I.
(c) Statement-I is correct but statement-II is wrong.
(d) Statement-I is wrong but statement-II is correct
Answer:
(a) Statement-I and II are correct and statement-II is correct explanation of statement-I.

Question 6.
The shape of methyl free radicals is
a) Planar
b) Pyramidal
c) Tetrahedral
d) Linear
Answer:
a) Planar

Question 7.
Which one of the following is correct order of the stability of carbanions?
(a) ^–C(CH₃)₃> ^–CH(CH₃)₂> ^–CH₂-CH₃> ^–CH₃
(b) ^–CH₃> ^–CH₂-CH₃> ^–CH(CH₃)₂> ^–C(CH₃)₃
(c) ^–CH(CH₃), > ^–CH₃> ^–CH₂-CH₃ > ^–C(CH₃)₃
(d) ^–CH₂-CH₃ > ^–CH(CH₃)₂> ^–CH₃> ^–C(CH₃)₃
Answer:
(b) CH₃> CH₂-CH₃> CH(CH₃)₂> C(CH₃)₃

Question 8.
Which of the following contains only three pairs of electrons
a) Carbocation
b) Carbanion
c) Free radical
d) All of these
Answer:
a) Carbocation

Question 9.
Which one of the following is not nucleophile
(a) H₂O
(b) NH₃
(c) R-OH
(d) FeCl₃
Answer:
(d) FeCl₃

Question 10.
In carbonium ion the carbon bearing the positive charge is
a) sp hybridized
b) sp² hybridized
c) sp³ hybridized
d) un hybridized
Answer:
b) sp² hybridized

Question 11.
Which one of the following is nucleophile?
(a) BF₃
(b) AlCl₃
(c) CO₂
(d) R-SH
Answer:
(d) R-SH

Question 12.
The geometry of a methyl carbanion is likely to be
a) Pyramidal
b) Tetrahedral
c) Planar
d) Linear
Answer:
a) Pyramidal

Question 13.
Which one of the following species has a tendency to show +I effect?
(a) -NH₂
(b) -Cl
(c) -C₆H₅
(d) -CH₃
Answer:
(d) -CH₃

Question 14.
Which one of the following has the strongest acidic character?
(a) HCOOH
(b) CH₃COOH
(c) CH₂ClCOOH
(d) CCl₃COOH
Answer:
(d) CCl₃COOH

Question 15.
Which one of the following has the least acidic character?
(a) HCOOH
(b) CH₃COOH
(c) CH₂ClCOOH
(d) CCl₃COOH
Answer:
(b) CH₃COOH

Question 16.
Electrophiles are
a) Electron loving species
b) Electron hating species
c) Nucleus loving reagents
d) Nucleus hating reagents
Answer:
a) Electron loving species

Question 17.
Statement-I: Fluoro acetic acid is stronger acid than acetic acid
Statement-II: Fluorine has high electronegativity and it is facilitate to dissociate the OH bond easily.
(a) Statement-I and II are correct and statement-II is correct explanation of statement-I.
(b) Statement-I and II are correct but statement-II is not correct explanation of statement-I.
(c) Statement-I is correct but statement-II is wrong.
(d) Statement-I is wrong but statement-Il is correct
Answer:
(a) Statement-I and II are correct and statement-II is correct explanation of statement-I.

Question 18.
Which one of the following is an example for negative mesomeric effect?
(a) -SH
(b) -SR
(c) -NH₂
(d) -NO₂
Answer:
(d) -NO₂

Question 19.
Methyl carbanium ion is
a) Electrophile
b) Lewis acid
c) Nucleophile
d) Both (a) and (b)
Answer:
c) Nucleophile

Question 20.
Identify the one which does not come under the organic addition reaction
(a) Hydration
(b) Dehydration
(c) Halogenation
(d) Hydro halogenation
Answer:
(b) Dehydration

Question 21.
Primary alcohols undergo which type of reaction to form alkenes?
(a) Elimination
(b) Oxidation
(c) Reduction
(d) Hydrolysis
Answer:
(a) Elimination

Question 22.
Identify the type of reaction
(a) Addition reaction
(b) Elimination reaction
(c) Reduction reaction
(d) Oxidation reaction
Answer:
(d) Oxidation reaction

II. Match the following.

Answer:

III. Fill in the blanks.
Question 1.
The slowest step in the mechanism determines ………..
Answer:
Rate of reaction

Question 2.
Homolytic cleavage occurs under the conditions of ………….
Answer:
High temperature.

Question 3.
During the cleavage of Azobisisobutyronitrile produces species ……….
Answer:
Free radical

Question 4.
The cleavage of C-Br bond in tert-butyl bromide leads to formation of ………..
Answer:
Carbocation

Question 5.
The cleavage of C-H bond in aldehydes Leads to formation of ………….
Answer:
Carbanion

Question 6.
Electron displacement occurring in saturated compounds along a carbon chain is termed as …………
Answer:
Inductive effect

Question 7.
The addition of H to alkene is an example of effect ……….
Answer:
+E

Question 8.
Example for positive mesomeric effect is ………..
Answer:
-OH

Question 9.
Acidity of phenol was explained by …………
Answer:
R-effect

Question 10.
Hydrolysis of alkyl halide is an example for ……….
Answer:
Nucleophilic substitution

Question 11.
4-hydroxy phenol reacts with acidified potassium dichromate to gives
Answer:
p-Benzoquinone

Question 12.
Enzyme present in apple is
Answer:
Polyphenol oxidase

Question 13.
Benzene reacts with H₂ in the presence of Pt to give
Answer:
Cyclohexane

Question 14.
Alcohol on refluxing with K₂Cr₂O₇ gives……..
Answer:
Carboxylic acid

Question 15.
Carbonyl compounds especially ketones undergo reduction to form ………..
Answer:
Secondary alcohols

Question 16.
Ethane undergoes thrombolytic cleavage to form ………..
Answer:
Methyl free radical

IV. Choose the odd one out.
Question 1.
(a) NH₃
(b) H₂O
(c) CN^–
(d) RSH
Answer:
(c) CN^– It is a negatively charged nucleophile whereas others are neutral nucleophiles.

Question 2.
(a) CO₂
(b) RX
(c) MCl₃
(d) FeCl₃
Answer:
(b) RX. It is a positive charged electrophiles whereas others are neutral electrophiles.

Question 3.
(a) -F
(b) – Cl
(c) – COOH
(d) CH₃O^–
Answer:
(d) CH₃O^–. It is a group carrying negative charge one electron-donating (or) +I group whereas others are -I group.

Question 4.
(a) – C(CH₃)₃
(b) – COOK
(c) – CH(CH₃)₂
(d) – COO^–
Answer:
(b) – COOH. It has -I effect whereas others have a +I effect.

Question 5.
(a) -OH
(b) -NH₂
(c) -SH
(d) -COOH
Answer:
(d) – COOH. It has a negative mesomeric effect whereas others have a positive mesomeric effect.

V. Choose the correct pair.
Question 1.
(a) Homolytic clevage : carbocation
(b) Homolytic clevage : carbanion
(c) Homolytic clevage : free radicals
(d) Heterolytic clevage : free radicals
Answer:
(c) Homolytic clevage : free radicals

Question 2.
(a) + C(CH₃)₃ > ⁺CH(CH₃)₂> ⁺CH₂-CH₃ > ⁺CH₃ : Relative stability of carbocations.
(b) – C(CH₃)₃ > ^–CH(CH₃)₂ > ^–CH₂-CH₃ > ^–CH₃ : Relative stability of carbanion.
(c) OH^–,RO^–, RCOO^– : Neutral nucleophile
(d) AlCl₃, BF₃, FeCl₃ : Positively charged nucleophile
Answer:
(a) + C(CH₃)₃ > ⁺CH(CH₃)₂> ⁺CH₂-CH₃ > ⁺CH₃ : Relative stability of carbocations.

Question 3.
(a) CH₃ – CH₂ – CH₂Br + Alcoholic KOH : Substitution reaction
(b) CH₃ – CH₂ – CH₂Br + Alcoholic KOH : Elimination reaction
(c) CH₃CHO + Acidic dichromate : Reduction reaction
(d) Benzene + Pt + H₂ : Oxidation reaction
Answer:
(b) CH₃ – CH₂ – CH₂Br + Alcoholic KOH : Elimination reaction

VI. Choose the incorrect pair.
Question 1.
(a) – OH,- SH, -NH₂ : Positive mesometic effect
(b) – NO₂ >CO, – COOH : Negative mesomeric effect
(c) – F, – Cl, – NO₂ : Electron withdrawing group
(d) – C(CH₃)₃, – CH(CH₃)₃ – CH₂ – CH₃ : Electron withdrawing group
Answer:
(c) – F, – Cl, – NO₂ : Electron withdrawing group

Question 2.
(a) NH₃ andAmines : Neutral nucleophile
(b) OH^– and RCOO^– : Negative nucleophile
(c) RX and H₃O₃ : Positive electrophile
(d) MCl₃, BF₃ : Negative electrophile
Answer:
(d) AlCl₃, BF₃ : Negative electrophile

Question 3.

Answer:

VII. Assertion and Reason.
Question 1.
Assertion (A): Neutral molecule SnCl₄ can act as an electrophile.
Reason (R): it has vacant ‘d’ orbitais which can accommodate the electrons from others.
(a) Both (A) and (R) are correct and (R) is the correct explanation of (A).
(b) Both (A) and (R) are correct but (R) is not the correct explanation of (A).
(c) (A) is correct but (R) is wrong.
(d) (A) is wrong but (R) is correct.
Answer:
(a) Both (A) and (R) are correct and (R) is the correct explanation of (A).

Question 2.
Assertion (A) : The C-C bond in ethane is non-polar while the C-C bond in ethyl chloride is polar.
Reason (R) : Chlorine is more electronegative than carbon and hence it attracts the shared pair of electron between C-C in ethyl chloride and it develops a negative charge on Cl and positive charge on Carbon.
(a) Both (A) and (R) are correct but (R) is not the correct explanation of (A).
(b) Both (A) and (R) are correct and (R) is the correct explanation of (A).
(c) (A) is correct but (R) is wrong.
(d) (A) is wrong but (R) is correct.
Answer:
(b) Both (A) and (R) are correct and (R) is the correct explanation of (A).

Question 3.
Assertion (A): Phenol is more acidic than aliphatic alcohols.
Reason (R): The phenoxide ion is more stabilized than phenol by resonance effect and hence resonance favours ionization of phenol to form H and shows acidity.
(a) Both (A) and (R) are correct and (R) is the correct explanation of(A).
(b) Both (A) and (R) are correct but (R) is not the correct explanation of(A).
(c) (A) is correct but (R) is wrong.
(d) (A) is wrong but (R) is correct.
Answer:
(a) Both (A) and (R) are correct and (R) is the correct explanation of(A).

Question 4.
Assertion (A): The cut apple turns brown.
Reason (R): Cut apple exposes its cells to atmospheric oxygen and the oxidizes the phenolic compound present in it. Due to this enzymatic browning, the cut apple turns brown.
(a) Both (A) and (R) are correct but (R) is not the correct explanation of (A).
(b) Both (A) and (R) are correct and (R) is the correct explanation of (A).
(c) (A) is correct but (R) is wrong.
(d) (A) is wrong but (R) is correct.
Answer:
(b) Both (A) and (R) are correct and (R) is the correct explanation of (A).

Samacheer Kalvi 11th Chemistry Basic Concepts of Organic Reactions 2 Marks Question and Answers

II. Answer briefly.

Question 1.
What is the mechanism of reaction?
Answer:
Many chemical reactions are depicted in one or more simple steps. Each step passes through an energy barrier, leading to the formation of short-lived intermediates or transition states. The series of simple steps which collectively represent the chemical change, from the substrate to product is called the mechanism of the reaction. The slowest step in the mechanism determines the overall rate of the reaction.

Question 2.
What is the mechanism of the reaction?
Answer:
In organic reactions, that series of simple steps collectively represent the chemical change, from the substrate to product, this is called as the mechanism of the reaction. The slowest step in the mechanism determines the overall rate of the reaction.

Question 3.
What is the Negative Mesomeric effect? Give example.
Answer:
The negative resonance effect occurs when the electrons move towards the substituent attached to the conjugated system. It occurs if the electron-withdrawing substituents are attached to the conjugated system. In such cases, the attached group has a tendency to withdraw electrons through resonance. These electron-withdrawing groups are usually denoted as -R or -M groups.
Example:
NO₂, > C = O, – COOH, – C ≡ N etc..

Question 4.
Explain the homolytic fission of a covalent bond?
Answer:

• Homolytic cleavage is the process in which a covalent bond breaks symmetrically in such way that each of the bonded atoms retains one electron.
• This type of cleavage occurs under high temperatures or in the presence of UV light.
• in a compound containing a non-polar covalent bond formed between atoms of similar electronegativity, in such molecules the cleavage of bonds results in free radicals.
• For example, ethane undergoes homolytic fission to produce, two methyl free radicals.
  

Question 5.
What are free radical initiators?
Answer:
The types of reagents that promote homolytic cleavage in substrate are called as free radical initiators. They are short lived and are highly reactive.

Question 6.
Mention any two examples for free radical initiators?
Answer:
Two examples for free radical initiators

• Azobisisobutyronitnie (AIBN)
• Benzoyl peroxide

Question 7.
Explain the heterolytic fission of a covalent bond?
Answer:

• Heterolytic cleavage is the process in which a covalent bond breaks unsymmetrically such that one of the bonded atom retains the bond pair of electron.
• It results in the formation of a cation and an anion of the two bonded atoms the most electronegative.
• For example in tert-butyibromide, the C-Br bond is polar as bromine is more electronegative than carbon. Hence the C-Br undergoes heterolytic cleavage to form a terl-butyl carbocation and bromide anion.
  

Question 8.
What are carbocations?
Answer:
1. Let us consider the heterolytic fission of the bond C-X present in organic molecule. If atom X has a greater electronegativity than the carbon atom, the former takes away the bonding electron pair and becomes negatively charged while the carbon will lose its electron and thus acquire a positive charge.
2. Such a cationic species carrying a positive charge on carbon are known as carbocation or carhonitim ion.

Question 9.
What are carbanions?
Answer:
Let us consider the heterolytic fission of the bond C-X present in an organic molecule. if the carbon atom has greater electronegativity than the atom X, the former takes away the bonding electron pair and acquires a negative charge. The resulting carbon anion is known as carbanion.

Question 10.
After cutting an apple it turns brown. Why?
Answer:
Apples contain an enzyme called polyphenol oxidase (PPO), also known as tyrosinase. Cutting an apple exposes its cells to atmospheric oxygen and oxidizes the phenolic compounds present in apples. This is called the enzymatic browning that turns a cut apple brown. In addition to apples, enzymatic browning is also evident in bananas, pears, avocados and even potatoes.

Question 11.
Identify which of the following are electrophiles and nucleophiles?

1. NH₃
2. AlCl₃
3. R-SH
4. R-X
5. R-O-R
6. BF₃

Answer:

Question 12.
How will you distinguish between electrophiles and nucleophiles?
Answer:
Electrophiles:

• They are electron deficient.
• They are cations.
• They are lewis acids.
• Accept an electron pair.
• Attack on electron-rich sites.

Nucleophites:

• They are electron-rich.
• They are anions.
• They are lewis bases.
• Donate an electron pair.
• Attack on electron-deficient sites.

Question 13.
What are all the sources for the human body that produces free radicals?
Answer:
Sources for the human body produces free radicals,

• The human body is exposed to X-rays.
• Cigarette smoke.
• Industrial chemicals.
• Air pollutants.

Question 14.
In what way free radicals affect the human body?
Answer:

• Free radicals can disrupt cell membranes.
• Increase the risk of many forms of cancer.
• Damage the interior lining of blood vessels.
• leads to a high risk of heart disease and stroke.

Question 15.
How to reduce the effect of free radicals?
Answer:

• Use vitamins and minerals to counter the effects of free radicals.
• Fruits contain antioxidants which decrease the effects of free radicals.

Question 16.
Identify which of the following shows the +I and -I effect?

1. -NO₂
2. -SO₂H
3. -I
4. -OH
5. CH₂O-
6. CH₂–

Answer:

Question 17.
Why chloro acetic acid is stronger acid than acetic acid?
Chioro acetic acid:
Answer:

Chioro acetic acid has Cl-group and it has high electronegativity and shows -I effect. Therefore Cl-atom to faciLitate the dissociation of O-H bond very fastly, whereas in the case of acetic acid, has CH₃ group and it shows +I effect, theretòre dissociation of O-H bond will be more difficult. Thus chloro acetic acid is stronger acid than acetic acid.

Question 18.
Explain the positive and negative electromeric effects?
Answer:
1. When an electrophile such as W approaches an alkene molecule, the π electrons are instantaneously shifted to the electrophile and a new bond is formed between carbon and hydrogen. This makes the other carbon electron deficient and hence it acquires a positive charge.

2. When the it electron is transferred towards the attacking reagent, it is called the positive electromeric (+E) effect.

3. Whèn the t electron is transferred away from the attacking reagent it is called the negative electromeric (-E) effect.

For example : The attack of C\({ N }^{ \ominus }\) on a carbonyl carbon.

Question 19.
Write short notes on the positive mesomeric effect?
Answer:

• The positive mesomeric effect occurs, when the electrons move away from substituent attached to the conjugated system.
• It occurs if the electron releasing substituents are attached to the conjugated system.
• The attached group has a tendency to release electrons through resonance, these electron releasing groups are usually denoted as +R or +M groups.
• Examples: -OH, -SH, -OR, -SR, -NH₂ etc.

Question 20.
Write short notes on the negative mesomeric effect?
Answer:

• The negative mesomeric effect occurs when the electrons move towards the substituent attached to the conjugated system.
• It occurs if the electron-withdrawing substituents are attached to the conjugated system.
  The attached group has a tendency to withdraw electrons through resonance, these electron-withdrawing groups are usually denoted as -R or -M groups.
• Examples:
  

Question 21.
What are addition reactions? Give an example.
Answer:
All organic compounds having double or triple bond adopt addition reactions in which two substances unite to form a single compound. During the addition reaction the hybridization of the substrate changes as only one bond breaks and two new bonds are formed.
Example:

Question 22.
What are elimination reactions? Give an example.
Answer:
In these reactions, two atoms or groups are removed from a molecule without being substituted by other atoms or groups. A new C-C double bond is formed between the carbon atoms to which the eliminated atoms or groups are previously attached. It is always accompanied with change in hybridization.
Example:

Question 23.
What are organic oxidation reactions? Give an example.
Answer:
Most of the oxidation reaction of organic compounds involves gain of oxygen or loss of hydrogen.
Example:

Question 24.
What are organic reduction reactions? Give an example.
Answer:
Most of the reduction reaction of organic compounds involves the gain of hydrogen or loss of oxygen.
Example:

Question 25.
Why cut apple turns a brown colour?
Answer:

• Apples contain an enzyme called polyphenol oxidase (PPO) also known as tyrosinase.
• Cutting an apple exposes its cells to atmospheric oxygen and oxidizes the phenolic compounds present in apples. This is called the “enzymatic browning” that turns a cut apple brown.
• In addition to apples, enzymatic browning is also evident in bananas, pears, avocados, and even potatoes.

Question 26.
What are the different types of organic reactions?
Answer:
Organic compounds undergo many reactions, however, in the actual sense, we can fit all those reactions into the below-mentioned six categories.

1. Substitution reactions
2. Addition reactions
3. Elimination reactions
4. Oxidation and reduction reactions
5. Rearrangement reactions
6. Combination of the above

Question 27.
How will you convert alcohol into aldehyde?
Answer:
When primary alcohol reacts with acidified potassium dichromate to gives aldehyde.

Question 28.
What happen when nitrile undergoes acid hydrolysis?
Answer:
When alkyl nitrile undergoes acid hydrolysis to give amide, which on further hydrolysis to give carboxylic acid.

Question 29.
Complete the following reactions and identify the products?
Answer:

Question 30.
Predict the product for the following reaction.
Answer:

Answer:

Question 31.
How will you convert benzene into cyclohexane?
Answer:
Benzene undergo catalytic hydrogenation in presence of platinum to give cyclohexane.

Question 32.
Complete the reaction and name the product

Answer:

Question 33.
Identify the product and mention the type of organic reaction.
Answer:

This is one of the elimination reaction.

Question 34.
Complete the following reaction and identify the product.
Answer:

Question 35.
What are substitution reaction?
Answer:
In this reaction an atom or a group of atoms attached to a carbon atom is replaced by a new atom or a group of atoms.

Here, -Br is replaced by -OH group.

Question 36.
How will substitution reactions are classified?
Answer:
Substitution reactions can be classified as,

• Nucleophilic substitution reaction.
• Electrophilic substitution reaction.
• Free radical substitution reaction.

Question 37.
Draw the resonance structures for the following compounds?

Answer:

Question 38.
Identify the reagents shown in box in the following equations as nucleophiles or electrophiles.
Answer:

In (a) \(\overset { \ominus }{ OH } \) is nucleophile
In (b) \(\overset { \ominus }{ CN } \) is nucleophile
In (c) CH₃\(\overset { \ominus }{ CO } \) is electrophile

Question 39.
Classify the following reactions in one of the reaction type of organic reaction.
Answer:
(a) CH₃CH₂Br + \({ SH }^{ \ominus }\) → CH₃CH₂SH + \({ Br }^{ \ominus }\)
(b) (CH₃)₂C = CH₂ + HCI (CH₃)₂CCl – CH₃
(c) CH₃CH₂Br + \({ OH }^{ \ominus }\) → CH₂ = CH₂ + H₂O + \({ Br }^{ \ominus }\)
(a) Nucleophilic substitution reaction.
(b) Electrophilic addition reaction.
(c) Elimination reaction.

Question 40.
Which electron displacement effect explain the following correct orders of acidity of the carboxylic acids?
Answer:
CH₃CH₂COOH > (CH₃)₂ CHCOOH > (CH₃)₃C COOH
As the number of alkyl group increases, +I effect increases and it strengthen the O-H bond. i.e., O-H bond dissociation is very difficult.

Therefore +I effect explain the correct orders of acidity of the carboxylic acids.

Question 41.
Which of the two, NO₂CH₂CH₂\({O}^{ \ominus }\) or CH₃CH₂\({O}^{ \ominus }\) is expected to be more stable and why?
Answer:

(I) is more stable than (II) because NO₂ group has -I effect and hence it tends to disperse the -ve charge on the 0-atom. In contrast., CH₃CH, has +I effect. It therefore, tends to intensify the -ve charge and hence destabilizes it.

Samacheer Kalvi 11th Chemistry Basic Concepts of Organic Reactions 5 Marks Questions and Answers

Question 1.
Explain electron movement in organic reactions.
Answer:
All organic reactions can be understood by following the electron movements.

• Lone pair becomes a bonding pair.
• Bonding pair becomes a lone pair.
• A bond breaks and becomes another bond.

The electron movement depends on the nature of the substrate, reagent and the prevailing conditions.
Type – 1.
A lone Pair to a bonding pair

Type – 2.
A bonding pair to a lone Pair

Type – 3.
A bonding pair to an another bonding pair

Question 2.
How does inductive effect influence the reactivity and acidity of carboxylic acids?
Answer:
(a) Reactivity:

• When a highly electronegative atom such as halogen is attached to a carbon then it makes the C—X bond polar.
• In such cases the -I effect of halogen facilitates the attack of an incoming nucleophile at the polarized carbon and hence increases the reactivity.
  
• If a -I group is attacher neared to a carbonyl carbon, it decreases the availability of electron density on the carbonyl carbon and hence increases the rate of the nucleophilic addition reaction.

(b) Acidity of carboxylic acid:

• When a halogen atom is attached to the carbon which is neared to the carboxylic acid group, its -I effect withdraws the bonded electrons towards itself and makes the ionization of H+ easy.
• The acidity of various chioro acetic acid is in the following order. Cl₃C-COOH > Cl₂CHCOOH > ClCH₂COOH The strength of the acid increases with increase in the effect of the group attached to the carboxyl group.
• Similarly the following order of acidity in the carboxylic acids is due to the +1 effect of alkyl group. (CH₃)₃CCOOH < (CH₃)₂CHCOOH <CH₃COOH

Question 3.
Explain the acidic nature of phenol.
Answer:

• Resonance is useful in explaining certain properties such as acidic of phenol.
• The phenoxide ion is more stabilized than phenol by resonance effect.
• The resonance favours ionisation of phenol to form H+ and shows acidity.
  
  phenoxide ion resonance structures.
  
• The above structures shows that there is a charge separation in the resonance structure of phenol which needs energy whereas there is no such hybrid structures in the case of phenoxide ion. This increases stability accounts for the acidic character of phenol.

Question 4.
How does the hyperconjugation effect explain the stability of alkenes?
Answer:

• The relative stability of various classes of carhonium ions may be explained by the number of no-bond resonance structures that can be written for them.
• Such structures are arrived by shifting the bonding electrons from an adjacent C-H bond to the electron-deficient carbon.
• in this way, the positive charge originally on carbon is dispersed to the hydrogen. This manner of electron release by assuming no bond character in the adjacent C-H bond is called hyperconjugation or Baker- Nathan effect.
• The greater the hyperconjugation, the greater will be the stability of the compound. The increasing order of stability can be shown as:
  
• Alkyl group increases in the C=C double bond carbon, hyperconjugation increases, and stability of that organic compound also increases.

Question 5.
Explain the types of addition reactions?
Answer:
Addition reactions are classified into three types. They are,

1. Electrophilic addition reaction
2. Nucleophilic addition reaction
3. Free radical addition reaction

1. Electrophilic addition reaction:
An electrophilic addition reaction can be described as an addition reaction in which a reactant with multiple bonds as in a double or triple bond undergoes has it air bond broken and two new a bond are formed.

2. Nucleophilic addition reaction:
A nucleophilic addition reaction is an addition reaction where a chemical compound with an electron-deficient or electrophilic double or triple bond, reacts with a nucleophilic which is an electron-rich reactant with the disappearance of the double bond and creation of two new single or bonds.

3. Free radical addition reaction:
it is an addition reaction in organic chemistry involving free radicals. The addition may occur between a radical and a non radical or between two radicals.

Question 6.
Explain the types of substitution reaction?
Answer:
Substitution reactions are classified into three types. They are,

1. Nucleophilic substitution reaction.
2. Electrophilic substitution reaction.
3. Free radical substitution reaction.

1. Nucleophilic substitution reaction:
A nucleophilic substitution reaction in organic chemistry is a type of reaction where a nucleophilic gets attached to the positive charged atoms or molecules of the other substance. A good example of a nucleophilic substitution reaction is the hydrolysis of alkyl bromide, under the basic conditions where in the nucleophile is nothing but the base H. whereas the leaving group is the Br°. The reaction for the following is as give below.

2. Electrophilic substitution reaction:
The electrophilic substitution reaction involves the electrophiles. The electrophilic reactions occur mostly with the aromatic compounds. This types of substitution reaction arc basically defined as those chemical reactions where the electrophile replaces the functional group in a compound but not the hydrogen atom, sometimes hydrogen atom can be also replaced by electrophiles.
For example:

3. Free radical substitution reaction:
Free radical substitution reaction involving free radicals arc a reactive intermediate.
A – X + Y → A – Y + X
CH₄ + Cl → CH + HCl
CH₃ + Cl → CH₃Cl (methyl chloride)

Question 7.
For the following bond cleavages use curved-arrows to show the electron flow and classify each as homolytic or heterolytic fission. Identify reactive intermediate produced as free radical,, carbocation and carbanion?

Answer:

Question 8.
An organic compound (A) has a molecular formula C₂H₆O it is one of the primary alcohol. A reacts with acidified potassium dichromate to give B. B on further undergoes to oxidation reaction to give C. C on reacts with SOCl₃ to give D which ¡s chlorinated product. Identify A,B,C and D, explain with equation.
Answer:
1. C₂H₆O is CH₃-CH₂-OH which is a primary alcohol (A)
2. CH₃-CH₂-OH (A) reacts with H⁺/ K₂Cr₂O₇ to give acetaldehyde (B)

3. CH₃CHO (B) which on further oxidation to give acetic acid (C).

4. Acetic acid reacts with SOCl₂ to give acetyl chloride (D).

Question 9.
An organic compound (A) of a molecular formula C₂H₄ which is a simple alkene. A reacts with dil H₂S0₄ to give B. A again reacts with Cl₂ to give C. Identify AB and C and write the equations.
Answer:
1. C₂H₂ is CH₂=CH₂ is a simple alkene. A is ethylene.
2. Ethylene (A) reacts with dii H₂SO₄ to give ethanol (B)

3. Ethylene (A) reacts with Cl, to give 1.2 dichloro ethane (C)

Question 10.
Complete the reactions and identify the products.
Answer:

Students can Download Chemistry Chapter 15 Environmental Chemistry Questions and Answers, Notes Pdf, Samacheer Kalvi 11th Chemistry Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Chemistry Solutions Chapter 15 Environmental Chemistry

Samacheer Kalvi 11th Chemistry Environmental Chemistry Textual Evaluation Solved

Samacheer Kalvi 11th Chemistry Environmental Chemistry Multiple Choice Questions

Question 1.
Th gaseous envelope around the earth is known as atmosphere. The region lying between an altitude of 11-50 km is –
(a) Troposphere
(b) Mesophere
(c) Thermosphere
(d) Stratosphere
Answer:
(d) Stratosphere

Question 2.
Which of the following is natural and human disturbance in ecology?
(a) Forest fire
(b) Floods
(c) Acid rain
(d) Greenhouse effect
Answer:
(a) Forest fire

Question 3.
Bhopal Gas Tragedy is a case of –
(a) thermal pollution
(b) air pollution
(c) nuclear pollution
(d) land pollution
Answer:
(b) air pollution

Question 4.
Haemoglobin of the blood forms carboxyhaemoglobin with –
(a) Carbon dioxide
(b) Carbon tetrachioride
(c) Carbon monoxide
(d) Carbonic acid
Answer:
(c) Carbon monoxide

Question 5.
Which sequence for greenhouse gases is based on GWP?
(a) CFC > N₂O > CO₂ > CH₄
(b) CFC > CO₂ > N₂O > CH₄
(c) CFC > N₂O > CH₄ > CO₂
(d) CFC > CH₄ > N₂O > CO₂
Answer:
(c) CFC > N₂O > CH₄ > CO₂

Question 6.
Photo chemical smog formed in congested metropolitan cities mainly consists of –
(a) Ozone, SO₂ and hydrocarbons
(b) Ozone, PAN and NO₂
(c) PAN, smoke and SO₂
(d) Hydrocarbons, SO₂ and CO₂
Answer:
(b) Ozone, PAN and NO₂

Question 7.
The pH of normal rain water is –
(a) 6.5
(b) 7.5
(c) 5.6
(d) 4.6
Answer:
(c) 5.6

Question 8.
Ozone depletion will cause –
(a) forest fires
(b) eutrophication
(c) bio magnification
(d) global warming
Answer:
(d) global warming

Question 9.
Identify the wrong statement in the following.
(a) The clean water would have a BOD value of more than 5 ppm
(b) Greenhouse effect is also called as Global warming
(c) Minute solid particles in air is known as particulate pollutants
(d) Biosphere is the protective blanket of gases surrounding the earth
Answer:
(a) The clean water would have a BOD value of more than 5 ppm

Question 10.
Living in the atmosphere of CO is dangerous because it –
(a) Combines with O₂ present inside to form CO₂
(b) Reduces organic matter of tissues
(c) Combines with haemoglobin and makes it incapable to absorb oxygen
(d) Dries up the blood
Answer:
(c) Combines with haemoglobin and makes it incapable to absorb oxygen

Question 11.
Release of oxides of nitrogen and hydrocarbons into the atmosphere by motor vehicles is prevented by using –
(a) grit hamber
(b) scrubbers
(c) trickling filters
(d) catalytic convertors
Answer:
(c) trickling filters

Question 12.
Biochemical oxygen Demand value less than 5 ppm indicates a water sample to be
(a) highly polluted
(b) poor in dissolved oxygen
(c) rich in dissolved oxygen
(d) low COD
Answer:
(c) rich in dissolved oxygen

Question 13.
Match the list I and list II and select the correct answer using the code given below in the list:

Answer:

Question 14.
Match the list I and list II and select the correct answer using the code given below in the list

Answer:

Question 15.
Assertion (A) : if BOD level of water in a reservoir is more than 5 ppm it is highly polluted.
Reason(R) : High biological oxygen demand means high activity of bacteria in water
(a) (i)
(b) (ii)
(c) (iii)
(d) (iv)
Answer:
(d) (iv)

Question 16.
Assertion (A) : Excessive use of chlorinated pesticide causes soil and water pollution.
Reason (R) : Such pesticides arc non-biodegradable.
(a) (i)
(b) (ii)
(c) (iii)
(d) (iv)
Answer:
(a) (i)

Question 17.
Assertion (A) : Oxygen plays a key role in the troposphere.
Reason (R) : Troposphere is not responsible for all biological activities
(a) (i)
(b) (ii)
(c) (iii)
(d) (iv)
Answer:
(d) (iv)

Samacheer Kalvi 11th Chemistry Environmental Chemistry Short Answer Questions

Question 18.
Dissolved oxygen in water is responsible for aquatic life. What processes are responsible for the reduction in dissolved oxygen in water’?
Answer:

• Organic matter such as leaves, grass, trash can pollute water. Microorganisms present in water can decompose these organic matter and consume dissolved oxygen in water.
• Eutrophication is a process by which water bodies receive excess nutrients that stimulates excessive plant growth. This enhanced plant growth in water bodies is called algal bloom.
• The growth of algae in extreme abundance covers the water surface and reduces the oxygen concentration in water. Thus, bloom-infeded water inhibits the growth of other. living organisms in the water body.
• This process in which the nutrient rich water support a dense plant population, kills animal life by depriving it of oxygen and results in loss of biodiversity is known as eutrophication.

Question 19.
What would happen, if the greenhouse gases were totally missing in the earth’s atmosphere?
Answer:

• The primary greenhouse gases in Earth’s atmosphere are water vapour, carbon dioxide, methane, nitrous oxide and ozone.
• Naturally occurring greenhouse gases allow solar radiations to reach the earth’s surface, while trapping radiations from the earth on its way back out to space.
• There would he no life on Earth without the warmth provided by this natural greenhouse gases.
• In the absence of greenhouse gases. the average temperature of the earth will decrease drastically. As a result. life on Earth would be impossible.

Question 20.
Define smog.
Answer:

• Smog is a combination of smoke and fog which form droplets that remains suspended in the air.
• Smog is a chemical mixture of gases that forms a brownish yellow haze. It mainly consists of ground level ozone, oxides of nitrogen, volatile organic compounds, SO₂, acidic aerosols and some other gases.

Question 21.
Which is considered to be earth’s protective umbrella? Why?
Answer:

• At high altitudes in the atmosphere consists of a layer of ozone (O₂) which acts as an umbrella for harmful UV radiations. Ozone is considered to be earth’s protective umbrella.
• It protects us from harmful effects of UV-radiations of the sun such as skin cancer.
• Ozone layer prevent the UV radiations to reach the earth surface. So it acts as an umbrella for the Earth.

Question 22.
What are bio-degradable and non-biodegradable pollutants?
Answer:

• The pollutants which can be easily decomposed by the natural biological processes are called biodegradable pollutants. For example plant wastes, animal wastes.
• The pollutants which cannot be decomposed by the natural biological processes are called non-biodegradable pollutants. For example, metal wastes such as Hg and Pb, D.D.T. plastics, nuclear vastcs.

Question 23.
From where does ozone come in the photochemical smog?
Answer:

• Photochcrnical smog is formed by the combination of smoke, dust and fog with air pollutants in the presence of sunlight.
• Chemically it is oxidising in nature because of high concentration of oxidising agents such as NO₂ and O₂. So it is also called oxidising smog.
• Photochemical smog is formed by following reactions:
• N₂ + O₂ → 2NO
  2NO + O₂ → 2NO₂
  
  (O) + O₂ → O₃
  O₃ + NO → NO₂ + O₂
  
• NO and O₃ arc strong oxidizing agents and they can react with unburnt hydrocarbons in polluted air to form formaldehyde, acrolcin and PAN.

Question 24.
A person was using water supplied by corporation. Due to shortage of water he started using underground water. He felt laxative effect. What could be the cause?
Answer:
Drinking water containing moderate level of sulphatcs is harmless. But excessive concentration (>500 ppm) of suiphates in drinking water causes laxative effect.

Question 25.
What is green chemistry?
Answer:

• Green chemistry is a chemical philosophy encouraging the design of products and processes that reduces or eliminates the use and generation of hazardous substances.
• Efforts to control environmental pollution resulted in development of science for the synthesis of chemicals favorable to environment.
• Green chemistry means science of environmentally favorable chemical synthesis.

Question 26.
Explain how does greenhouse effect cause global warming.
Answer:

• The earth’s atmosphere allows most of the visible light from the sun to pass through and reach the earth’s surface. As earth’s surface is heated by sunlight, it radiates a part of this energy back towards the space as longer IR wavelengths.
• Some of the heat is trapped by CH₂, CO₂. CFCs and water vapour present in the atmosphere. They absorb IR radiations and block a large portion of earth’s emitted radiations.
• The radiations thus absorbed is partly remitted to the earth’s surface. Therefore the earth’s surface gets heated up by a phenomenon called greenhouse effect.
• Thus greenhouse effect is defined as the heating up of the earth surface due to trapping of infrared radiations reflected by earth’s surface by CO₂ layer in the atmosphere. The heating up of the earth through the greenhouse effect is called global warming.

Question 27.
Mention the standards prescribed by BIS for quality of drinking water.
Answer:
Standard characteristics prescribed for deciding the quality of drinking water by BIS are as follows:

Question 28.
How does classical smog differ from photochemical smog?
Answer:
Classical smog:

• Classical smog is caused by coal-smoke and fog.
• It occurs in cold humid climate.
• The chemical composition is the mixture of SO₂, SO₃ gases and humidity.
• Chemically it is reducing in nature because of high concentration of SO, and so it is also called reducing smog.
• It is primarily responsible for acid rain.
• It also causes bronchial irritation.

Photochemical smog:

• Photochemical smog is cause by photochemical oxidants.
• It occurs in warm, dry and sunny climate.
• The chemical composition is the mixture of NO₂ and O₃ gases.
• Chemically it is oxidising in nature because of high concentration of oxidising agents such as NO₂ and O₃
• and so it is also called oxidising smog.
• It causes irritation to eyes, skin and lungs and increase the chances of asthma.
• It causes corrosion of metals, stones

Question 29.
What are particulate pollutants? Explain any three.
Answer:
1. Particulate pollutants are small solid particles, and liquid droplets suspended in air.
Examples:
dust, pollen, smoke, soot and liquid aerosols.

2. Types of Particulates:
Particulates in the atmosphere may be of two types:

• viable particulate and
• non-viable particulate.

3.The viable particulates are small size living organisms such as bacteria, fhngi, moulds and algae which are dispersed in air.

4. The non-viable particulates are small solid particles and liquid droplets suspended in air. There are four types of non-viable particulates in the atmosphere. They are
(a) Smoke
(b) Dust
(c) Mist
(d) Fumes

5. Smoke:
Smoke particulate consists of solid particles formed by combustion of organic matter. For example, cigarette smoke, oil smoke, smokes from burning of fossil fuels, garbage and dry leaves.

6. Dust:
It is composed of fine solid particles produced during crushing and grinding of solid materials. For example, sand from sand blasting, saw dust from wood works and fly ash from power generating units.

7. Mist:
They are formed by particles of sprayed liquids and condensation of vapours in air. For example, sulphuric acid mist, herbicides and insecticides sprays can form mists.

8. Fumes:
They are obtained by condensation of vapours released during sublimation, distillation, boiling and calcination and by several other chemical reactions.
For example:
organic solvents, metals and metallic oxides.

Question 30.
Even though the use of pesticides increases the crop production, they adversely affect the living organisms. Explain the function and the adverse effects of the pesticides.
Answer:
1. Pesticides are the chemicals that are used to kill or stop the growth of unwanted organims. But these pesticides can affect the health of human beings. Pesticides are classified as
(a) insecticides,
(b) Fungicides and
(c) Herbicides.

(a) Insecticides:
Insecticides like DDT, BHC, Aidrin can stay in soil for a long period of time and are absorbed by soil. They contaminate root crops like carrot, radish.

(b) Fungicides:
Organomercury compounds dissociate in soil to produce mercury which is highly toxic.

(c) Herbicides:
They are used to control unwanted plants and are also known as weed killers. Eg, Sodium chlorate, sodium nitrate. They are toxic to mammals.

Question 31.
Ethane bums completely in air to give CO₂. while in a limited supply of air gives CO. The same gases are found in automobile exhaust. Both CO and CO₂ are atmospheric pollutants

1. What is the danger associated with these gases?
2. How do the pollutants affect the human body?

Answer:
Danger associated with CO and CO₂ & health hazards to human body
(a) Carbon monoxide binds with haemoglohin and form carboxyhaemoglobin which impairs normal oxygen transport by blood and hence the oxygen carrying capacity of blood is reduced. This oxygen deficiency results in headache, tension, dizziness, loss of consciousness, blurring of eyesight and cardiac arrest.

(b) Increase in CO₂ level in the atmosphere is responsible for global warming. It causes headache and nausea.

Question 32.
On the basis of chemical reactions involved, explain how do CFC’s cause depletion of ozone layer in stratosphere?
Answer:
(i) The chioro-Iluoro derivatives of methane and ethane are named Freons (CFC’s). They slowly pass from troposphere to stratosphere. They stay for a very longer period of about 50-100 years. In the presence of UV radiations, CFC’s break up into chienne free radicals.

Cl• + O₃ → { ClO }^{ \bullet } + O₂
ClO• + O → { Cl }^{ \bullet } + O₂

(iii) Chlorine radical is regenrated in the course of the reaction. Due to this continuous attack of Cl free radicals, thinning of ozone layer takes place which leads to the formation of ozone hole.

(iv) Li is estimated that for every reactive chlorine atom generated in the stratosphere 1,00,000 molecules of ozone are depleted.

Question 33.
How is acid rain formed? Explain its effect.
Answer:
1. Rain water has a pli of 5.6 due to the dissolution of CO., into it. Oxides of sulphur and nitrogen in the atmosphere may be absorbed by droplets of water that make up the clouds and get chemically converted into sulphuric acid and nitric acid. Due to this the pH of rain water drops below the level of 5.6. Hence it is called acid rain.

2. Acid rain is a by-product of sulphur and Nitrogen oxides in the atmosphere. Burning of fossil fuels in power stations, furnaces and petrol, diesel in motor engines produce SO₂ and NO₂ gases. They are converted into H₂SO₄ and HNO₃ by the reaction with oxygen and water.

3. 2SO₂ + O₃ + 2H₂O → 2H₂SO₄
4NO₂ + O₂+ 2H₂O → 4HNO₃

Harmful effects of acid rain:
1. Acid rain causes damage to buildings made us of marbles. This attack on marble is termed as stone leprosy.
CaCO₃ + H₂SO₂ CaSO₄ + H₂O + CO₂↑

2. Acid rain affects plant and animal life in aquatic ecosystem.

3. It is harmful For agriculture, as it dissolves in the earth and removes the nutrients needed for the growth of plants.

4. It corrodes water pipes resulting in the leaching of heavy metals such as iron, lead and copper into drinking water which have toxic effects.

5. it causes respiratory ailment in humans and animals.

Question 34.
Differentiate the following:

1. BOD and COD
2. Viable and non-viable particulate pollutants

Answer:
Biochemical oxygen demand (BOD):

• The total amount of oxygen (in milligrams) consumed by microorganisms in decomposing the waste in one litre ut water at 20°C for a period of 5 days is called biochemical oxygen demand (BOD).
• its value is expressed in ppm.
• DOD is used as a measure of degree ofwater pollution.
• BOD is only a measurement of consumed oxygen by microorganims to decompose the organic matter.
  Clean water would have BOD value less than 5 ppm.

Chemical ox gen demand (COD):

• Chemical oxygen demand is defined as the amount of oxygen required by the organic matter in a sample of water for its oxidation by a strong oxidising agent like K₇Cr₂O₇ in acidic medium for a period of 2 hours.
• Its value is expressed in mg / litre.
• COD is a measure of amount of organic compounds in a water sample.
• COD refers to the requirement of dissolved oxygen for both the oxidation of organic and inorganic constituents.
• Clean water would have COD value greater than 250 mg/litre.

2. Viable and non-viable particulate pollutants
Viable pollutants:

• The viable particulates are small size living organisms such as bacteria, fungi. moulds, algae which are dispersed in air.
• They are all organic particulates.
• They contain living organisms.
•  Eg. ftingi, bacteria, algae, moulds. Viable particles are the particles with at least one microorganism affecting the sterility of the product.

Non-viable pollutants:

• The non-viable particulates are small solid particles and liquid droplets suspended in air.
• They are all inorganic particulates.
• They contain non-living organisms.
• Eg. Smoke, dust, mist, fumes.
• Non-viable particles are the particles without microorganisms but act as transporting agent for viable particles.

Question 35.
Explain how oxygen deficiency is caused by carbon monoxide in our blood? Give its effect.
Answer:

1. Carbon monoxide binds with haemoglobin and form carboxy the haemoglobin which impairs normal oxygen transport by blood and hence the oxygen carrying capacity of blood is reduced.
2. This oxygen deficiency results in headache, dizziness, tension, loss of consciousness, blurring of eyesight and cardiac arrest.

Question 36.
What are the various methods you suggest lo protect our environment from pollution?
Answer:
Methods to control environmental pollution:

• Waste management Environmental pollution can be controlled by proper disposal of wastes.
• Recycling A large amount of disposed waste materials can he reused by recycling the waste, thus it reduces the landfill. –
• By substitution of less toxic solvents for highly toxic ones are used in industrial processes.
• By growing more trees.
• By using fuels with lower sulphur content.
• By control measures in vehicle emissions which are adequate.

Samacheer Kalvi 11th Chemistry Environmental Chemistry Additional Questions Solved

I. Choose the correct answer

Question 1.
Which one of the following is bio-degradable pollutant?
(a) DDT
(b) Plastics
(c) Mercury
(d) Wood
Answer:
(d) Wood

Question 2.
Which one of the following gases is not present in troposphere?
(a) N₂O₂
(b) CO₂
(c) N₂
(d) water vapours
Answer:
(c) N₂

Question 3.
Which of the following pair of’ oxides is responsible for acid rain?
(a) SO₃ + NO₂
(b) CO₂ + CO
(c) N₂O + CH₄
(d) O₂ + H₂
Answer:
(a) SO₃ + NO₂

Question 4.
Which one of the following is produced as a result of incomplete combustion of coal’?
(a) CO₂
(b) CO
(c) SO₂
(d) SO₃
Answer:
(b) CO

Question 5.
Which of the following is not a greenhouse gas’?
(a) CO
(b) O₃
(c) CH₄
(d) Water vapours
Answer:
(a) CO

Question 6.
Photochemical smog occurs in warm, dry and sunny climate. One of the following is not among-st the components of photochemical smog. Identify it.
(a) NO₂
(b) O₃
(c) SO₂
(d) Unsaturated hydrocarbons
Answer:
(c) SO₂

II. Match the following
1.

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

III. Fill in the blanks

Question 1.
An example for biodegradable pollutant is ………
Answer:
plant waste.

Question 2.
An example for non-biodegradable pollutant ………
Answer:
metal waste.

Question 3
……… is the lowest layer of atmosphere.
Answer:
Troposphere.

Question 4.
Ozone is present in ……… layer of the atmosphere.
Answer:
Stratosphere.

Question 5
……… is called blue planet.
Answer:
Earth.

Question 6.
About 80% of the mass of the atmosphere is present in ………
Answer:
Troposphere.

Question 7.
……… will reduce the oxygen carrying capacity of blood.
Answer:
CO

Question 8
……… gas is used in the process of photosynthesis.
Answer:
CO₂

Question 9.
……… gas potentially damage plant leaves and retard photosynthesis.
Answer:
NO₂

Question 10.
……… is formed by incomplete combustion of coal.
Answer:
CO₂

Question 11.
……… binds with haemoglobin and reduce the oxygen carrying capacity of blood.
Answer:
CO

Question 12.
……… is carcinogenic and causes irritation in eyes and mucous membrane.
Answer:
PAH

Question 13.
The earths surface get heated up by a phenomenon called ………
Answer:
Greenhouse effect

 

Question 14.
The main constituent of layer responsible for global warming is ………
Answer:
CO₂

Question 15.
Earth’s average surface temperature would be only about ………
Answer:
-18°C

Question 16.
The pH of rain water is normally ………
Answer:
5.6

Question 17.
……… pair of compounds is present in acid-rain water.
Answer:
HNO₃ + H₂SO₄

Question 18.
……… is an example of viable particulate.
Answer:
Bacteria.

Question 19.
……… is an example of non-viable particulate matter.
Answer:
Cement dust.

Question 20.
Particulate pollutants will result in the health hazard named as ………
Answer:
pneimoconiosis.

Question 21.
Coal miners may suffer from ………
Answer:
Black lung disease.

Question 22.
Textile workers may suifer from ………
Answer:
White lung disease.

Question 23.
………….. aftect childrcns brain. interfers with maturation of RBC’s and even causes cancer.
Answer:
Lead.

Question 24.
……… can be used to reduce particulate pollutant.
Answer:
electrostatic precipitator

Question 25.
……… is the combination of smoke and fog.
Answer:
Smog.

Question 26.
Classical smog called London smog contains ………
Answer:
Coal-smoke and fog.

Question 27.
Classical smog is otherwise called ………
Answer:
reducing smog.

Question 28.
Photochemical smog is otherwise called ………
Answer:
Los angeles smog.

Question 29.
The three main components of photochemical sinog are ………
Answer:
Hydrogen sulphide. dust and PAN.

Question 30.
……… plantation can metabolise nitrogen oxide and control photochemical smog.
Answer:
Pinus tree.

Question 31.
……… acts as an umbrella for the earth and prevent harmful UV radiations.
Answer:
ozone.

Question 32.
……… pair of compounds is found to be highly responsible for depletion of ozone layer.
Answer:
Nitric oxide + CFC

Question 33.
Freons are ………
Answer:
Chiorofluoroalkanes.

Question 34.
Ozone layer is depicted by the reactive ………
Answer:
Chlorine atom.

Question 35.
Examples for water borne diseases are ………
Answer:
Dysentery and cholera.

Question 36.
The standard pH of drinking water is ………
Answer:
6.5 to 8.5

Question 37.
The essential elements for soil are ………
Answer:
N,P,K

Question 38
……… is a better alternative for carnicogentic benzene.
Answer:
Xylene.

Question 39.
The alternate solvent used instead of tetrachioroethYlefle in dry cleaning is ………
Answer:
Liquefied CO₂

Question 40.
……… is used for bleaching clothes in laundry.
Answer:
H₂O₂

Question 41.
……… is used to bleach paper.
Answer:
H₂O₂

Question 42.
……… is the most safest pesticide.
Answer:
Neem based pesticide.

Question 43.
……… acid is most abundant ¡n acid rain.
Answer:
H₂SO₄

Question 44.
……… causes less pollution.
Answer:
CO₂

Question 45.
Besides CO₂ the other greenhouse gas is ………
Answer:
CH₄

Question 46.
BOD is a measure of ………
Answer:
Organic pollutant in water.

Question 47.
The pollutant released in Bhopal gas tragedy was ………
Answer:
Methyl isocyanate.

Question 48.
The greatest affinity for haemoglobin in shown by ………
Answer:
CO

Question 49.
Eutrophication causes reduction in ………
Answer:
dissolved oxygen.

IV Choose the odd one out

Question 1.
(a) Plant waste
(b) DDT
(c) Plastic
(d) Nuclear waster
Answer:
(a) Plant waste. It is biodegradable pollutant whereas others are non-biodegradable pollutants.

Question 2.
(a) Plant waste
(b) Animal wastes
(c) Paper
(d) Nuclear waste
Answer:
(d) Nuclear waste. It is non-biodegradable pollutant whereas others are biodegradable wastes.

Question 3.
(a) N₂O₂
(b) CO₂
(c) H₂O (Vap)
(d) O₃
Answer:
(d) O₃ It is present in stratosphere whereas others are present in troposphere.

Question 4.
(a) O₂⁺
(b) O⁺
(c) N₂
(d) NO⁺
Answer:
(c) N₂. ills present in mesosphere whereas others are present in thermosphere.

Question 5.
(a) N₂
(b) O₂
(c) O₃
(d) N₂O₂
Answer:
(d) N₂O₂ It is present in troposphere whereas others are present in stratosphere.

Question 6.
(a) CH₄
(b) CO
(c) CO₂
(d) CFC
Answer:
(b) CO. It is a poisonous gas whereas others are responsible for green house effect.

V. Choose the correct pair

Question 1.
(a) CCF : Green house effect
(b) CO : Carcinogenic
(c) PAH : Acid rain
(d) NO : Lung injury
Answer:
(a) CCF : Green house effect

Question 2.
(a) NO₂ : Green house effect
(b) CFC : asthma and lung injury
(c) PAH : carcinogenic
(d) CO₂ : green house effect
Answer:
(a) NO₂ : Green house effect

Question 3.
(a) Classical smog : NO₂ and O₂
(b) London smog : SO₂, SO₂ and humidity
(c) Photochemical smog : CO₂ and CO
(d) Los Angel smog : NO₂ and NO₃
Answer:
(b) London smog : SO₂ , SO₂ and humidity

VI. Choose the incorrect pair

Question 1.
(a) Photochemical smog : NO₂ and O₂
(b) Classical smog : SO₂, SO₃ and humidity
(c) Smog : Smoke and fog
(d) Non viable particulate : Algae, Fungi
Answer:
(d) Non viable particulate : Algae, Fungi

Question 2.
(a) Viable particulate : bacteria, fungi
(b) Non viable particulate : smoke, dust
(c) Acid rain : HCl + HNO₂
(d) Photochemical smog : NO₂ + O₃
Answer:
(c) Acid rain : HCl + HNO₂

Question 3.
(a) Lead : Damage to kidney, liver
(b) Sulphate : Laxative effect
(c) Nitrage : Blue baby syndrome
(d) TDS : Damage to bone and teeth
Answer:
(d) TDS : Damage to bone and teeth

Question 4.
(a) Insecticides : DDT. BCHs
(b) Herbicides : Organo mercury compounds
(c) Herbicides : Sodium chlorate, sodium arsenite
(d) Industrial waste : Mercury. copper
Answer:
(b) Herbicides : Organo mercuiy compounds

VII. Assertion & Reason
Assertion (A) : Depletion of ozone layer causes skin cancer.
Reason (R) : Depletion olozone layer will allow more UV rays to reach the earth surface and cause skin cancer.
(a) Both (A) and (R) are correct and (R)is the correct explanation of (A).
(b) Both (A) and (R) are correct but (R) is not the correct explanation of (R).
(c) (A) is correct but (R) is wrong.
(d) (A) is wrong but (R) is correct.
Answer:
(a) Both (A) and (R) are correct and (R) is the correct explanation of (A).

Question 2.
Assertion (A) : UV radiations damages the fish productivity.
Reason (R) : UV radiations affect the growth of phytoplankions as a result food chain in ocean is disturbed.
(a) Both (A) and (R) are correct hut (R) is not the correct explanation of (A).
(b) Both (A) and (R) are correct and (R) is the correct explanation of (A).
(c) (A) is correct but (R) is wrong.
(d) (A) is wrong but (R) is correct.
Answer:
(b) Both (A) and (R) are correct and (R) is the correct explanation of (A).

Question 3.
Assertion (A) : The pH ol acid rain is less than 5.6.
Reason (R) : CO, present in the atmosphere dissolves in rain water and forms carbonic acid,
(a) Both (A) and (R) are correct and (R) is the correct explanation of (A).
(b) Both (A) and (R) are correct hut (R) is not correct explanation of (A).
(c) (A) is correct bitt (R) is wrong.
(d) (A) is wrong but (R) is correct.
Answer:
(a) Both (A) and (R) are correct and (R) is the correct explanation of (A).

Samacheer Kalvi 11th Chemistry Environmental Chemistry 2 Mark Questions and Answers

Question 1.
What is meant by environmental pollution?
Answer:
Any undesirable change in our environment that have harmful effects on plants. animals and human beings is called environmental pollution.

Question 2.
Write a note on constituents of earth’s atmosphere.
Answer:
Earth’s atmosphere is a layer of gases retained by earth’s gravity. it contains roughly 78% Nitrogen, 21% Oxygen. 0.93% Argon, 0.04% Carbon dioxide. traces of other gases and little amount of water vapour. This mixture is commonly known as air.

Question 3.
What is called troposphere? How many layers are present in it? Give their names.
Answer:

1. The lowest layer of the atmosphere is called the troposphere and il extends from 0 10 km from the earth surface.
2. About 80% of the mass of the atmosphere is in this layer. 3 layers are present in it.
3. They are –
   • Hydrosphere
   • Lithosphere
   • Biosphere

Question 4.
Write about hydrosphere (or) Why Earth is called as Blue planer?
Answer:

• Hydrosphere include all types of water sources like oceans, seas, rivers, lakes. streams, underground water, polar ice-caps, clouds etc.
• It covers about 75% of the earth’s surface. Hence earth is called as Blue planet.

Question 5.
What is lithosphere?
Answer:
Lithosphere includes soil, rocks and mountains which are solid components of Earth.

Question 6.
What is biosphere?
Answer:
Biosphere includes the lithosphere. hydrosphere and atmosphere integrating the living organisms present in the lithosphere, hydrosphere and atmosphere.

Question 7.
What is air pollution?
Answer:
Air pollution is defined as any undesirable change in air which adversely affects living organisms. Air pollution is limited to troposphere and stratosphere.

Question 8.
What are the types of air pollutants? Give examples.
Answer:
1. Air pollutants exists in two major forms namely:
(a) Gaseous air pollutants
(b) Particulates

2. Gaseous air pollutants:
Oxides of sulphur, oxides of nitrogen, oxides of carbon and hydrocarbons are the gaseous air pollutants.

3. Particulate pollutants:
Particulate pollutants are small solid particles and liquid droplets suspended in air.
Exarnple:
dust, pollen, smoke, soot, aerosols.

Question 9.
Define greenhouse effect.
Answer:
Greenhouse effect is defined as the heating up of the earth’s surface due to trapping of infrared radiations reflected by earth’s surface by the CO₂ layer in the atmosphere.

Question 10.
What is Global warming?
Answer:
The heating up of the earth through the greenhouse effect is called Global warming.

Question 11.
When rain water is named as acid rain?
Answer:
Rain water normally has a pH of 5.6 due to dissolution of atmospheric CO₂ particles into it. Oxides of sulphur and nitrogen in the atmosphere are absorbed by droplets of water that make up clouds and get chemically converted into sulphuric acid and nitric acid. As a result the pH of rainwater drops below 5.6 and hence it is called acid rain.

Question 12.
What is stone leprosy? How is it formed?
Answer:

• The attack on the marble of buildings by acid rain is called stone leprosy.
• Acid rain causes extensive damage to buildings made up of marble CaCO + H₂SO₄ CaSO₄ + H₂O + CO₂↑

Question 13.
What are fumes? Give one example.
Answer:
Fumes are one of the non-viable particulate pollutants air. They are obtained by condensation of vapours released during sublimation, distillation, boiling and calcination. For example, organic solvents, metals and metallic oxides form fume particles.

Question 14.
What are the techniques to reduce particulate pollutants?
Answer:
The particulates from air can be removed by using electrostatic precipitators, gravity settling chambers, wet scrubbers or by cyclone collectors. These techniques are base on washing away or settling of the particulate matter.

Question 15.
How will you control photochemical smog?
Answer:
The formation of photochemical smog can be suppressed by preventing the release of nitrogen oxide and hydrocarbons into the atmosphere from the motor vehicles by using catalytic convertors in engines. Plantation of certain trees like Pinus, Pyrus Querus vitus and Juniparus can metabolise nitrogen oxide.

Question 16.
What is meant by water pollution’?
Answer:
Water pollution is defined as the addition of foreign substances or factors like heat which degrades the quality of water so that it becomes an health hazard or unfit for use.

Question 17.
What are the sources of water pollution? Give examples.
Answer:

• The water pollutants originate form both natural as well as human activities. The source of water pollution are classified as point and non-point sources.
• Easily identified source of water pollution is called a point source. For example, Municipal and industrial discharge pipes.
• Non-point source cannot be identified easily. For example, agricultural runoffs, mining wastes, acid rain, storm water drainage and construction sediments.

Question 18.
What is BOD’?
Answer:
The total amount of oxygen (in milligrams) consumed by microorganisms in decomposing the waste in one litre of water at 20°C for a period of 5 days is cal Led biochemical oxygen demand (BOD) and its value is expressed in ppm.

Question 19.
What is COD?
Answer:
Chemical oxygen demand (COD) is defined as the amount of oxygen required by the organic matter in a sample of water for its oxidation by a strong oxidising agent like K₂Cr₂O₇ in acidic medium for a period of 2 hours.

Question 20.
What are total dissolved solids (TDS)?
Answer:

• Most of the salts are soluble in water. It include cations like calcium, magnesium, sodium, potassium, iron and anions like carbonate, bicarbonate, chloride, sulphate, phosphate and nitrate.
• Use of drinking water having TDS (total dissolved solids) concentration higher than 500 ppm causes possibilities of irritation in stomach and intestine.

Question 21.
What are the constituents of soil?
Answer:
Soil is a thin layer of organic and inorganic material that covers the earth’s rocky surface. Soil constitutes the upper crust of the earth, which supports land, plants and animals.

Question 22.
Define – soil pollution.
Answer:
Soil pollution is defined as the build up of persistent toxic compounds, radioactive materials, chemical salts and disease causing agents in soil which have harmful effects on plant growth and animal health. Soil pollution affects the structure and fertility of soil, ground water quality and food chain in biological ecosystem.

Question 23.
Explain how industrial waste affects the soil.
Answer:

• Industrial activities have been the biggest contributor to soil pollution especially the mining and manufacturing activities.
• Industrial wastes include cyanides. chromates, acids, alkalis and metals like mercury, copper, zinc, cadmium and lead.
• These industrial wastes in the soil surface lies for a long time and makes it unsuitable for use.

Question 24.
What is green chemistry?
Answer:

• Efforts to control environment pollution have resulted in the development of chemicals favorable for environment and this branch of science is called green chemistry.
• It is a chemical philosophy encouraging the design of products and processes that reduces or eliminates the use and generation of hazardous substances.

Question 25.
Write a note about dry cleaning of clothes.
Answer:
Solvents like tetrachioroethylene is used in dry cleaning of clothes, pollute the ground water and are carcinogenic. In place of tetrachloroethylene liquefied CO₂ with suitable detergents an alternate solvent used. Liquefied CO₂ is not that much harmful for the groundwater. Nowadays H₂O₂ is used for bleaching clothes in laundry that give better results and utilises less water.

Question 26.
Carbon monoxide gas is more dangerous than carbon dioxide gas. Why?
Answer:
Carbon monoxide gas combines with haemoglobin to form a very stable compound known as carboxy haemoglobin. When its concentration in blood reaches 3-4%, the oxygen carrying capacity of the blood is greatly reduced. This results into headache, nervousness and sometimes death of the person. On the other hand CO₂ does not combine with haemoglobin and hence it is less harm ful than CO.

Question 27.
Which gases are responsible for greenhouse effect? List some of them.
Answer:
CO, is mainly responsible for greenhouse effect. Other greenhouse gases are methane, nitrous oxide, water vapours, CFCs and ozone.

Question 28.
A large number of fishes are suddenly found floating dead on a lake. There is no evidence of toxic dumping but you find an abundance of phytoplankton. Suggest a reason for the fish killing.
Answer:
Excessive phytoplankton (organic pollutants such as leaves, grass trash etc.) growth which is present in water is biodegradable. Bacteria decomposes this organic matter in water. During this process when large number of bacteria decomposes the organic matter, they consume the dissolved oxygen in water. When the level of dissolved oxygen falls below 6 ppm then the fishes cannot survive and they die.

Question 29.
How carbon monoxide acts as a poison for human beings’?
Answer:
Carbon monoxide is a poisonous gas because it combines with haemoglobin of RBC to form carboxyhaernoglobin as:
CO + Haemoglobin ⇌ Carboxyhaemoglobin
It inhibits the transport of oxygen to different pans of the body. Thus the body becomes oxygen-starved.

Question 30.
Give three examples in which the principles green chemistry has been applied.
Answer:

• In dry-cleaning, use of liquefied CO₂ in place of non-environment friendly tetrachioroethene (Cl₂C = CCl₂).
• Use of H₂O₂ in bleaching in place of chlorine.
• In the manufacture of chemicals like ethanal by using environment-friendly chemicals and conditions. ,

Samacheer Kalvi 11th Chemistry Environmental Chemistry 3 Marks Questions and Answers

Question 1.
Write about Bhopal gas tragedy.
Answer:

• On 3rd Decembers. 1984 at Bhopal city in India, by the early morning, an explosion at Union carbide pesticide plant released a cloud of toxic gas (Methyl isocyanate) CH₃NCO into the air.
• Since the gas is twice as heavy as air, it did not drift away but formed a blanket over the surrounding area.
• It attacked people’s lungs and affect their breathing staying there or in the nearby areas. Thousands of peopic died and lives of many were ruined. The lungs, brain, eyes, muscles as well as gastrointestinal, neurological and immune system of those people who survived were severely affected.

Question 2.
Explain how the oxides of sulphur pollute the atmospheric air. Give its haririful eflects.
Answer:

• Sulphur dioxide and sulphur trioxide are produced by burning sulphur containing fossil fuels and by roasting of suiphide ores.
• SO₂ is a poisonous gas for both animals and plants. SO₂ causes eye irritation, coughing and respiratory diseases like asthma, bronchitis.
• SO₂ is oxidised to more harmful SO₃ gas in the presence of particulate matter present in the polluted air:
  
  SO₂ combines with atmospheric water vapour to form H₂SO₄ which comes down along with rain in the form of acid rain:
• Acid rain causes stone leprosy. affect aquatic ecosystem, corrode water pipes and causes respiratory ailment in humans and animals.

Question 3.
How oxides of nitrogen are harmful?
Answer:
(i) Oxides of nitrogen are produced during high temperature combustion processes, by oxidation of nitrogen in air and it is formed the combustion of fuels such as coal, diesel and petrol.

(iii) The oxides of nitrogen are converted into nitric acid which comes down in the form of acid rain. They also form reddish brown haze in heay traffic.
(iv) Nitrogen dioxide potentially damage plant leaves and retard photosynthesis.
(v) NO₂ is a respiratory irritant and it can cause asthma and lung injury.

Question 4.
Explain how hydrocarbons pollute the atmospheric air.
Answer:

• The compounds composed of carbon and Hydrogen only are called hydrocarbons. They are mainly produced naturally and also by incomplete combustion of automobile fuels.
• They are potential cancer causing (carcinogenic) agents.
• For example polynuclear aromatic hydrocarbons (PAH) are carcinogenic, they cause irritation in eyes and mucous membranes.

Question 5.
Write flotes about great London smog.
Answer:

• The great smog of London (1952) was an instance of severe air pollution that affected the London from 5th December 9^th of December, 1952 and then dispersed quickly when the whether changed.
• It causes major disruption by reducing the visibility and even penetrating indoor areas.
• Government medical reports estimated that 4000 people had died as a direct result of smog and 100.000 were made ill by the smog effect on their respiratory tract.

Question 6.
What are the effects of classical smog?
Answer:

• Smog is primarily responsible for acid rain.
• Smog results in poor visibility and it affects air and road transport.
• It also causes bronchial irritation.

Question 7.
Explain how oxides of nitrogen are introduced directly into the stratosphere?
Answer:

• Nitrogen oxides are introduced directly into the stratosphere by the supersonic jet aircraft engines in the form of exhaust gases.
• These oxides arc released by combustion of fossil fuels and nitrogen fertilisers. Inert nitrous oxide in the stratosphere is photochemically converted into more reactive nitric oxide.
• Oxides of nitrogen catalyses the decomposition of ozone and are themselves regenerated. Ozone gets depleted as follows:
  
  Thus NO is regenerated in the chain reaction.

Question 8.
How chemical wastes pollute water?
Answer:

• A whole variety of chemicals from industries, such as metals and solvents are poisonous to fish and other aquatic life.
• Toxic pesticides can accumulate in fish and shell fish and poison the people who eat them.
• Detergents and oil float spoils the water bodies.
• Acids from mine drainage and salts from various sources can also contaminate water sources.

Question 9.
Explain the presence of fluoride in water and its hazardous effects?
Answer:

• Fluoride ion deficiency in drinking water causes tooth decay.
• The fluoride ions make the enamel on teeth much harder by converting hydroxyapatite
  [3(Ca₃(PO₄)₂. Ca(OFl)₂]. the enamel on the surface of the teeth into much harder fluorapatite [3(Ca₃(PO₃)₂. CaF₂]
• Fluoride ion concentration above 2 ppm causes brown mottling of teeth. Excess fluoride causes damage to bones and teeth.

Question 10.
Explain the harmful effects of

1. lead
2. Nitrate in drinking water.

Answer:

1. Drinking water containing lead contamination above 50 ppm can cause damage to liver, kidneys and reproductive system.
2. Use of drinking water having concentration of nitrates higher than 45 ppm may cause (blue baby syndrome) methemoglobinemia disease in chiidrens.

Question 11.
Explain how styrene is produced by traditional and greener routes?
Answer:
1. Traditional route:
This method involve two steps-Carcinogenic benzene reacts with ethylene to form ethyl benzene. After that ethyl benzene undergoes dehydrogenation using Fe₂O₃ / Al₂O₃ to give styrene.

2. Greener route:
To avoid carcinogenic benzene. greener routes to start with cheaper and
environment friendly xylene.

Question 12.
How acetaldehyde is commercially prepared by green chemistry?
Answer:
Acetaldehyde is commercially prepared by one step oxidation of ethene in the presence of ionic catalyst in aoiieniis medium with 9% yield.

Question 13.
What do you mean by ozone hole? What are its consequences?
Answer:
Depletion of ozone layer creates some sort of holes in the blanket of ozone which surrounds us in the atmosphere and this is known as ozone hole.

• With the depletion of the ozone layer, UV radiations filters into the troposphere which leads to ageing of skin. cataract, sunburn, skin cancer etc.
• By killing many of the phytoplanktons, it can damage the fish productivity.
• Evaporation rate increases through the surface and stomata of leaves which can decrease the moisture content of the soil.

Question 14.
What is photo chemical smog? What arc its effects? How can it be controlled?
Answer:
It is a kind of smog formed in warm, dry and sunny climate. It is formed when sunlight is absorbed by SO₂ oxides of nitrogen and hydrocarbons. It act as an oxidising agent.

Effects of photo chemical smog:

• It produces irritation in eyes and also in respiratory system.
• It can damage many materials such as metals, stones, building materials etc.
• NO₂ present in photochemical smog gives it brown colour which reduces the visibility.
• it is harmful to fabrics, crops and ornamental plants.

Control of photochemical smog:

• By using catalytic converters in automobilës.
• By spraying certain compounds into the atmosphere which generate free radicals that can easily combine with the free radicals that initiates the reaction forming toxic compounds of photochernical smog.
• Certain plants such as Pinus, Juniparus, Pyrus could be also helpful in this matter.

Question 15.
(a) Define eutrophication and pneumoconiosis.
(b) Write differences between photochemical smog and classical smog.
Answer:
(a) Eutrophication:
When the growth of algae increases in the surface of water, dissolved oxygen in water is greatly reduced. This phenomenon is known as eutrophication. Due to this growth of fishes gets inhibited.

(b) Pueumoconiosis:
It is a disease which irritates lungs. It causes scarring or fibrosis of the lungs.

Pholochemical smog:

• It is formed as a result of photochernical decomposition of nitrogen dioxide and chemical reactions involving hydrocarbons.
• It takes place during dry warm season in presence of sunlight.
• It is oxidising in nature.

Classical smog:

• It’s formed due to condensation of SO₂ vapours on particles of carbon in cold climate.
• it is generally formed during winter when there is severe cold.
• It is reducing in nature.

Samacheer Kalvi 11th Chemistry Environmental Chemistry 5 Marks Questions and Answers

Question 1.
Explain about the different layers of Earth’s atmosphere.
Answer:
Earth’s atmosphere can he divided into different layers with characteristic altitude and temperature.

Question 2.
What arc the health effects of particulate pollutants?
Answer:
1. Dust, mist, fumes etc. are air borne particles which are dangerous for human health. Particulate pollutants bigger than 5 microns are likely to settle in the nasal passage whereas particles of about 10 microns enter the lungs easily and causes scaring or fibrosis of lung lining.

They irritate the lungs and causes cancer and asthma. This disease is called pneumoconiosis. Coal miners may suffer from black lung disease. Textile workers may suffer from white lung disease.

2. Lead particulates affect children’s brain. interferes with maturation of RBC’s and even causes cancer.

3. Particulates in the atmosphere reduces the visibility by scattering and absorption of sun light. It is dangerous for aircraft and motor vehicles.

4. Particulates provide nuclei for cloud formation and increases fog and rain.

5. Particulates deposit on plant leaves and hinder the intake of CO₂ from the air and affect photosynthesis.

Question 3.
What arc the effects of photochernical smog?
Answer:

• The three main components of photochemical smog are nitrogen oxide, ozone and oxidized hydrocarbons like HCHO, CH₂ = CH – CRO and PAN.
• Photo chemical smog causes irritation to eyes. skin and lungs. It also increases the chance of asthma.
• high concentration of ozone and NO can cause nose and throat irritation, chest pain, difficulty in breathing.
• PAN is toxic to plants, attack younger leaves and cause bronzing and glazing of their surfaces.
• It causes corrosion of metals, stones, building materials and painted surfaces.

Question 4.
Explain about the environmental impacts of ozone depletion.
Answer:
1. The formation and destruction of ozone is a regular natural process, which never disturbs the equilibrium level of ozone in the stratosphere. Any change in the equilibrium level of ozone in the atmosphere will adversely affect the Life in biosphere in the following ways.
2. Depletion of ozone layer will allow more UV rays to reach the earth surface and would cause skin cancer and also decreases the immunity level in human beings.
3. UV radiations atlecis plant proteins which lead to harniful mutation in plant cells.
4. UV radiations affect the growth of phytoplankton and as a result ocean food chain is disturbed and it even damages the fish productivity.

Question 5.
Explain the list of major water pollutants and their sources.
Answer:

• Microorganisms – Domestic sewage, domestic waste water, dung heap
• Organic wastes – Domestic sewage, animal excreta, food processing factory wastc. detergents and decayed animals and plants
• Plant nutrients – Chemical fertilisers
• Heavy metals – Heavy metal producing factories
• Sediments – Soil erosion by agriculture and strip-mining
• Pesticides – Chemicals used for killing insects, fungi and weeds
• Radioactive substances – Mining of uranium containing minerals
• Heat – Water used for cooling in industries

Question 6.
Describe about the causes of water pollution.
Answer:
Causes of water pollution –
1. Microbiological pollutants:
(a) Disease causing microorganisms like bacteria, viruses and protozoa are most senous water pollutants. They come from domestic sewage and animal excreta.
(b) Fish and shellfish can become contaminated from them and people who eat them will also become ill.
(c) Dysentery and cholera are water borne diseases.
(d) Human excrcta contain bacteria such as Escherichia coll and Streptococcus farcical- -is which causes gastrointestinal diseases.

2. Organic wastes:
Organic matter such as leaves, grass, trash can also pollute water. Water pollution is cause by excessive phytoplankton growth within water.

3. Chemical wastes:
A whole variety of chemicals from industries such as metals and solvents are poisonous to fish and other aquatic life. Detergents and oils float spoils the water bodies. Acids from mine drainage and salts form various sources can also contaminate water sources.

Question 7.
What are the harmful effects of chemical water pollutants’?
Answer:

1. Cadmium and mercury can cause kidney damage.
2. Lead poisoning can lead to severe damage of kidneys. liver and brain. It also affects the central nervous system.
3. Polychiorinated biphenyl causes skin diseases and are carcinogenic in nature.

Question 8.
Explain about green chemistry in day-to-day life.
Answer:
1. Dry cleaning of clothes:
Solvents like tetrachloroethylene used in dry cleaning of clothes, pollute the ground water and are carcinogenic. In place of tetrachloro ethylene, liquefied CO₂ with suitable detergent is an alternate solvent used. Liquefied CO₂ is not harmful to the ground water. Nowadays H₂O₂ is used for bleaching clothes in laundry, gives better result and utilises less water.

2. Bleaching of paper:
Conventional method of bleaching was done with chlorine. Nowadays H₂O₂ can be used for bleaching paper in the presence of catalyst.

3. Synthesis of chemicals:
Acetaldehyde is commercially prepared by one step oxidation of ethene in the presence of ionic catalyst in aqueous medium with 90% yield.

4. Instead of petrol, methanol is used as a fuel in automobiles.
5. Neem based pesticides have been synthesis-ed, which are more safer than the chlorinated hydrocarbons.

Students can Download Commerce Chapter 30 Performance of Contract Questions and Answers, Notes Pdf, Samacheer Kalvi 11th Commerce Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Samacheer Kalvi 11th Commerce Solutions Chapter 30 Performance of Contract

Samacheer Kalvi 11th Commerce Performance of Contract Textbook Exercise Questions and Answers

I. Choose the Correct Answer

Question 1.
On the valid performance of the contractual obligations by the parties, the contract ………………..
(a) Is discharged
(b) Become enforceable
(c) Becomes void
(d) Becomes legal
Answer:
(a) Is discharged

Question 2.
Which of the following persons can perform the contract?
(a) Promisor alone
(b) Legal representatives of promisor
(c) Agent of the promisor
(d) All the above
Answer:
(d) All the above

Question 3.
A, B, C jointly promised to pay Rs.50,000 to D. Before performance of the contract, C dies. Here, the contract ………………..
(a) Becomes void on C’s death
(b) Should be performed by A and B along with C’s legal representatives.
(c) Should be performed by A and B alone.
(d) Should be renewed between A, B and D.
Answer:
(b) Should be performed by A and B along with C’s legal representatives.

Question 4.
Which of these parties cannot demand performance of promise?
(a) Promisee
(b) Any of the Joint Promisees
(c) On the death of a Promisee, his Legal Representative.
(d) Stranger to the Contract
Answer:
(d) Stranger to the Contract

Question 5.
A person is said to be a third person if he is not a ………………..
(a) promisor
(b) promise
(c) agent
(d) Legal Representative
Answer:
(c) agent

II. Very Short Answer Questions

Question 1.
State the ways of Performing a Contract.
Answer:
The following are the major ways of performance of a contract:

• Actual Performance
• Attempted Performance

Question 2.
Who is a Legal Representative?
Answer:
Legal representative can demand Exception performance. The contrary intention appears from the contract. The contract is of a personal nature.

Question 3.
Who is an agent?
Answer:
According to Para 2 of Section 40, the promisor may employ a competent person such as an agent to perform the promise if the contract is not formed on personal condition.

Question 4.
Define Reciprocal Promise.
Answer:
Promises which form consideration or part of the consideration for each other are called ‘reciprocal promise’.

Question 5.
By whom must contracts be performed?
Answer:
The contract will be performed only by the promisee.

III. Short Answer Questions

Question 1.
What is a Valid tender?
Answer:
A valid tender of performance is considered to be the performance of a promise.

Question 2.
Who can execute and Perform a Contract?
Answer:
The following persons can execute and perform the contract:

• Promisor himself
• Agent
• Representations
• Third-person
• Joint Promisors
• Time and Place of Performance of Promise ’

Question 3.
Who can demand performance?
Answer:

1. Promisee – only a promisee can demand performance and not a stranger demand performance of the contract.
2. Legal Representative – legal representative can demand Exception performance. Contrary intention appears from the contract. The contract is of a personal nature.
3. Third-party – Exception to “stranger to a contract”.

Question 4.
Write a note on the benefits of Reciprocal Promise.
Answer:
Promises which form consideration or part of the consideration for each other are called ‘reciprocal promise’. For example, X promises to sell his house to Y for Rs.5,00,000. The promises are reciprocal. X is the promisor to give the house and a promise to receive Rs.5,00,000. Y is the promise to receive the house and a promisor to pay Rs. 5,00,000.

Question 5.
Who is a Joint Promisors?
Answer:
According to Section 42 of the Indian Contract Act, there may be two or more creditors entitled to the same obligations, or two or more debtors under the same liability. Each of the debtors is bound in solidum (for the whole and not a proportional part). These persons are called joint promisors.

IV. Long Answer Questions

Question 1.
Explain rules relating to place of performance of promise.
Answer:
Time and place of Performance of Promise:
It is only the promisee for whom the contract is performed. Only the promisee can demand the performance of the promise under a contract.

For Example:
X promises Y to pay Z ₹ 10,000/-. X does not pay the sum to Z. Here Z cannot bind X for the payment. It is only promisee Y who can enforce the promise against the promisor X. Of course, there are certain special cases, where a third party can enforce a promise though he is not a party to the contract For example in respect of trust, marriage settlement etc. In case of death of promisee, the representative appointed by him can ask for the performance of the promise under a contract.

Question 2.
Elucidate the provision regarding time as factor in performance.
Answer:
Under Section 46, performance within a reasonable time: According to Section 46, a promisor is to perform his promise within a reasonable time. On the other hand, a reasonable time will depend upon the circumstance of the case, the usage of trade or on the intention of the parties entering into the contract. Example: A has given an order of supply of books in July which should be performed within 4 to 5 days of the month of July.

Question 3.
How do you think appropriation of payments takes place?
Answer:
Appropriation means the application of payments – The question of appropriation of payments arises when a debtor owes several debts to the same creditor and makes a payment that is not sufficient to discharge the whole indebtedness.

Appropriation of Payments: Sometimes, a debtor owes several distinct debts to the same creditor and he makes a payment which is insufficient to satisfy all the debts. In such a case, a question arises as to which particular debt the payment is to be appropriated. Section 59 to 61 of the Act lay down the following rules as to the appropriation of payments which provide an answer to this question.

Students can Download Economics Chapter 3 Production Analysis Questions and Answers, Notes Pdf, Samacheer Kalvi 11th Economics Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Economics Solutions Chapter 3 Production Analysis

Samacheer Kalvi 11th Economics Production Analysis Text Book Back Questions and Answers

Part – A

Multiple Choice Questions

Question 1.
The primary factors of production are:
(a) Labour and Organisation
(b) Labour and Capital
(c) Land and Capital
(d) Land and Labour.
Answer:
(d) Land and Labour.

Question 2.
The man-made physical goods used to produce other goods and services are referred to as …………………………
(a) Land
(b) Labour
(c) Capital
(d) Organization
Answer:
(c) Capital

Question 4.
Which factor is called the changing agent of society?
(a) Labourer
(b) Land
(c) Organizer
(d) Capital
Answer:
(c) Organizer

Question 5.
Who said, that one of the key of an entrepreneur is “uncertainty-bearing”.
(a) J.B.Clark
(b) Schumpeter
(c) Knight
(d) Adam Smith
Answer:
(c) Knight

Question 6.
The functional relationship between “inputs” and “outputs” is called………………………..
(a) Consumption Function
(b) Production Function
(c) Savings Function
(d) Investment Function
Answer:
(b) Production Function

Question 7.
In a firm 5 units of factors produce 24 units of the product. When the number of factor increases by one, the production increases to 30 units. Calculate the Average Product.
(a) 30
(b) 6
(c) 5
(d) 24
Answer:
(c) 5

Question 8.
The short-run production is studied through ………………………
(a) The Laws of Returns to Scale
(b) The Law of Variable Proportions
(c) Iso – quants
(d) Law of Demand
Answer:
(b) The Law of Variable Proportions

Question 9.
The long-run production function is explained by
(a) Law of Demand
(b) Law of Supply
(c) Returns to Scale
(d) Law of Variable Proportions
Answer:
(c) Returns to Scale

Question 10.
An Iso – quant curve is also known as …………………………
(a) Inelastic Supply curve
(b) Inelastic Demand Curve
(c) Equi – marginal Utility
(d) Equal Product Curve
Answer:
(d) Equal Product Curve

Question 11.
Mention the economies reaped from inside the firm
(a) Financial
(b) Technical
(c) Managerial
(d) All of the above
Answer:
(d) All of the above

Question 12.
Cobb – Douglas production function assumes ………………………….
(a) Increasing returns to scale
(b) Diminishing returns to scale
(c) Constant returns to scale
(d) All of the above
Answer:
(c) Constant returns to scale

Question 13.
Name the returns to scale when the output increases by more than 5%, for a 5% increase in the inputs,
(a) Increasing returns to scale
(b) Decreasing returns to scale
(c) Constant returns to scale
(d) All of the above
Answer:
(a) Increasing returns to scale

Question 14.
Which of the following is not a characteristic of land?
(a) It’s a limited supply
(b) It is mobile
(c) Heterogeneous
(d) Gift of Nature
Answer:
(b) It is mobile

Question 15.
The product obtained from additional factors of production is termed as
(a) Marginal product
(b) Total product
(c) Average product
(d) Annual product
Answer:
(a) Marginal product

Question 16.
Modem economists have propounded the law of ………………………
(a) Increasing returns
(b) decreasing returns
(c) Constant returns
(d) variable proportions
Answer:
(a) Increasing returns

Question 17.
Producer’s equilibrium is achieved at the point where:
(a) The marginal rate of technical substitution(MRTS) is greater than the price ratio
(b) MRTS is lesser than the price ratio
(c) MRTS and price ratio are equal to each other
(d) The slopes of Iso-quant and Iso-cost lines are different.
Answer:
(c) MRTS and price ratio are equal to each other

Question 18.
The relationship between the price of a commodity and the supply of a commodity is ……………………….
(a) Negative
(b) Positive
(c) Zero
(d) Increase
Answer:
(b) Positive

Question 19.
If the average product is decreasing, then the marginal product
(a) Must be greater than the average product
(b) Must be less than the average product
(c) Must be increasing
(d) Both a and c
Answer:
(b) Must be less than the average product

Question 20.
A production function measures the relation between ……………………….
(a) Input prices and output prices
(b) Input prices and the quantity of output
(c) The number of inputs and the quantity of output
(d) The number of inputs and input prices.
Answer:
(c) The number of inputs and the quantity of output

Part – B

Answer the following questions in one or two sentences

Question 21.
Classify the factors of production.
Answer:

1. Land: In Economics, land means all gifts of Nature owned and controlled by human beings which yield an income.
2. Labour: Labour means manual labour or unskilled work.
3. Capital: “Capital consists of all kinds of wealth other than free gifts of nature, which yield income”.
4. Bohm – Bawerk defines it as ‘a produced means of production’.
5. Organization: The man behind organizing the business is called as ‘Organizer’ or ‘Entrepreneur’.

Question 22.
Define labour?
Answer:

1. Labour is the active factor of production.
2. In common parlance, labour means manual labour or unskilled work. But in Economics the term ‘labour’ has a wider meaning.
3. It refers to any work undertaken for securing an income or reward. Such work may be manual or intellectual. For example, the work done by an agricultural worker or a cook, or rickshaw puller, or a mason is manual.
4. The work of a doctor or teacher or engineer is intellectual.
5. In short, labour in economics refers to any type of work performed by a labourer for earning an income.

Question 23.
State the production function.
Answer:

1. Production function refers to the relationship among units of the factors of production [inputs] and the resultant quantity of a good produced [out put].
2. According to George J. Stigler, the Production function is the relationship between inputs of productive services per unit of time and outputs of product per unit of time.

Question 24.
Define the Marginal Product of a factor?
Answer:
It is the addition or the increment made to the total product when one more unit of the variable input is employed. In other words, it is the ratio of the change in the total product to the change in the units of the input. It is expressed as
MP = ∆TP/∆N
Where MP = Marginal Product
∆TP = Change in total product
∆N = Change in units of input
It is also expressed as MP = TP [n] – TP [n-1]
MP = Marginal product
TP [n] = Total product of employing nth unit of a factor.
TP [n – 1] = Total product of employing the previous unit of a factor, that is, [n – 1]^th unit of a factor.

Question 25.
What is the Iso-cost line?
Answer:

1. The isocost line is an important component in analyzing the producer’s behaviour.
2. The isocost line illustrates all the possible combinations of two factors that can be used at given costs and for a given producer’s budget.
3. Simply stated, an isocost line represents different combinations of inputs which show the same amount of cost.
4. The isocost line gives information on factor prices and the financial resources of the firm.
5. It is otherwise called as “iso – price line” or “iso – income line” or “iso – expenditure line” or “total outlay curve”.

Question 26.
What are the conditions for the producer’s equilibrium?
Answer:
The two conditions that are to be fulfilled for the attainment of producer equilibrium are:

1. The isocost line must be tangent to the isoquant curve.
2. At the point of tangency, the isoquant curve must be convex to the origin or MRTSLk must be declining.

Question 27.
What are the reasons for the upward-sloping supply curve?
Answer:
A supply curve represents the data given in the supply schedule. As the price of the commodity increases, the quantum supplied of the commodity also increases. Thus the supply curve has a positive slope from left to right.

Part – C

Answer the following questions in One Paragraph

Question 28.
What are the characteristics of land?
Answer:

1. Land is a primary factor of production
2. Land is a passive factor of production
3. Land is the free gift of nature
4. Land has no cost of production
5. Land is fixed in supply. It is inelastic in supply
6. Land is permanent
7. Land is immovable
8. Land is heterogeneous as it differs infertility
9. Land has alternative uses
10. Land is subject to Law of Diminishing Returns.

Question 29.
What are the factors governing the elasticity of supply?
Answer:
1. Nature of the commodity:
Durable goods can be stored for a long time. So, the producers can wait until they get a high price. Once they get a higher price, a larger supply is possible. The elasticity of the supply of durable goods is high. But perishables are to be sold immediately. So perishables have a low elasticity of supply.

2. Cost of production:
When production is subject to either constant or increasing returns, additional production and therefore increased supply is possible. So elasticity of supply is greater. Under diminishing returns, an increase in output leads to high cost. So elasticity of supply is less.

3. Technical condition:
In large scale production with huge capital investment, supply cannot be adjusted easily. So elasticity of supply is lesser. Where capital equipment is less and technology simple, the supply is more elastic.

4. Time factor:
During a very short period when supply cannot be adjusted, the elasticity of demand is very low. In a short period, variable factors can be added and so supply can be adjusted to some extent. So elasticity of supply is more. In a long period, even the fixed factors can be added, and hence the supply is highly elastic.

Question 30.
What are the functions of entrepreneurs?
Answer:
Functions of an Entrepreneur:

• Initiation: An organizer is the initiator of the business, by considering the situation and availability of resources and planning the entire process of business of production.
• Innovation: A successful entrepreneur is always an innovator. He introduces new methods in the production process.
• Coordination: An organizer applies a particular combination of the factor of production to start and run the business or production.
• Control, Direction, and Supervision: An organizer controls so that nothing prevents the organization from achieving its goal. He directs the factors to get better results and supervises for the efficient functioning of all the factors involved in the process of production.
• Risk-taking and uncertainty-bearing: There are risk-taking and uncertainty-bearing obstacles. Risks may be insured but uncertainties cannot be insured. They reduce the profit.

Question 31.
State and explain the elasticity of supply.
Answer:
The elasticity of supply may be defined as the degree of responsiveness of change in supply to change in price on the part of sellers.
Mathematically:

Q – Supply, p – price, ∆ – change.

Question 32.
Bring out the Relationship among Total, Average and Marginal Products.
Answer:

Question 33.
Illustrate the concept of Producer’s Equilibrium.
Answer:
Producer equilibrium is the situation where the producer maximizes his output. It is also known as the optimum combination of the factors of production.
(Eg.) Maximum output at minimum cost.
Producer attains equilibrium where the Iso-cost line is tangent to the Iso-quant.

In the figure profit of the firm is maximised at the point of equilibrium.
At the point of equilibrium slope of the Iso-cost line = Slope of Iso-product curve At point E, the firm employs OM units of labour and ON units of capital which is the least cost combination.

Question 34.
State the Cobb – Douglas Production Function?
Answer:
The Cobb – Douglas Production Function was developed by Charles W. Cobb and Paul H. Douglas, based on their empirical study of the American manufacturing industry. It is a linear homogeneous production function which implies that the factors of production can be substituted for one another up to a certain extent only.

The Cobb – Douglas production function can be expressed as follows.
Q = AL²K²
Where, Q = output; A = positive constant;
K = capital;
L = Labor α and β are positive fractions showing, the elasticity coefficients of outputs for the inputs labor and capital, respectively.
P = (1 – a) since a + p = 1. denoting constant returns to scale.
Factor intensity can be measured by the ratio β / α.

The sum of α + β shows the returns to scale.

1. (α + β) = 1, constant returns to scale.
2. (α + β) < 1, diminishing returns to scale.
3. (α + β) >1, increasing returns to scale.

• The production function explains that with the proportionate increase in the factors, the output also increases in the same proportion.
• Cobb – Douglas production function implies constant returns to scale.
• Cobb – Douglas Production Function is a specific standard equation applied to describe how much output can be made with capital and labor inputs.

Part – D

Answer the following questions in about a page

Question 35.
Examine the Law of Variable Proportions with the help of a diagram.
Answer:
According to G. Stigler, “As equal increments of one input are added, the inputs of other productive services being held constant, beyond a certain point the resulting increments of the product will decrease (ie) the marginal product will diminish”.
Assumptions:

1. Only one factor is variable.
2. All units of the variable factor are homogeneous
3. The product is measured in physical units.
4. There is no change in the state of technology and the price of the product.

Stage of production:

Units of variable factor (labour) are employed along with other fixed factors. There are three stages of production.

Stage I:

1. In the first stage MP_L increases upto third labourer and is higher than the average product.
2. So that total produt is increasing at an increasing rate.

Stage II:

1. MP_L decreases up to the sixth unit of labour where MP_L curve intersects the x-axis.
2. The fourth unit of labour MP_L = AP_L
3. After this, MP_L curve is lower than the AP_L. TP_L increases at a decreasing rate.

Stage III:

1. The seventh unit of labour is marked by negative MP_L the AP_L continues to fall but positive.
2. TP_L declines with the employment of more units of labour.

Question 36.
List out the properties of Iso-quants with the help of diagrams.
Answer:
Iso-quant:
“An Iso-quant is a curve showing all possible combinations of inputs physically capable of producing a given level of output” – Ferguson.

Properties of Iso-quant curve:
1. The Iso-quant curve has a negative slope:

1. It slopes downwards from left to right indicating that the factors are substitutable.
2. In the diagram combination, A refers to more of capital K₅ and less of labour L₂
3. As the producer moves to B, C, and D more labour and less capital are used.

2. Convex to the origin:

1. In production, the capital substituted by 1 unit of labour goes on decreasing. It is called the diminishing marginal rate of technical substitution.
2. If the marginal rate of technical substitution diminishes the Iso-quants will be convex to the origin.
3. Constant MRTS (straight line) and increasing MRTS (concave).

3. Non-inter-section of Iso-Quant curves:

1. Point A lie on the Iso-quants IQ₁ and IQ₂
2. But the point C shows a higher output and point B shows a lower level of output IQ₁
3. If C = A, B = A, then C – B. But C > B which is illogical.
   

4. An upper Iso-quant curve represents a higher level of output:

1. Higher IQ_s show higher outputs and lower IQ_s show lower output.
2. The arrow in the figure shows an increase in the output with a right and upward shift of an Iso-quant curve.

5. Iso-quant curve does not touch either X-axis or Y-axis:
No Iso-quant curve touches the X-axis or Y-axis because in IQ, the only capital is used and in IQ₂ only labour is used.

Question 37.
Elucidate the Laws of Returns to Scale. Illustrate.
Answer:
Laws of Returns To Scale: In the long – run, there is no fixed factor; all factors are variable.
The laws of returns to scale explain the relationship between output and the scale of inputs in the long – run when all the inputs are increased in the same proportion.

Assumptions:
Laws of Returns to Scale are based on the following assumptions.

1. All the factors of production, [such as land, labour, and capital] are variable but the organization is fixed.
2. There is no change in technology.
3. There is perfect competition in the market.
4. Outputs or returns are measured in physical quantities.

Three Phases of Returns to Scale:

1. Increasing Returns to Scale: In this case, if all inputs are increased by one percent, output increase by more than one percent.
2. Constant Returns to Scale: In this case, if all inputs are increased by one percent, output increases exactly by one percent.
3. Diminishing Returns to Scale: In this case, if all inputs are increased by one percent, output increases by less than one percent.

In the diagram, the movement from point a to point b represents increasing returns to scale. Between these two points, input has doubled but the output was tripled.

The law of constant returns is implied by the movement from point b to point c. Between these two points inputs have doubled and output also has doubled.

Decreasing returns to scale are denoted by the movement from the point c to point d since doubling the factors from 4 units to 8 units produce less than the increase in inputs, that is by only 33.33%.

Question 38.
Explain the internal and external economies of scale.
Answer:
The scale of production is an important factor affecting production. Every producer wishes to reduce the costs of production by using economies of scale.
Marshall classified economies into two.
1. Internal economies of scale: Internal economies refer to the reduction in the cost of production of the commodity. They are of various types.

• Technical economies: When the size and capital of the firm is large, up-to-date technologies can be used to improve the productivity of the firm. Here research and development strategies can be applied easily.
• Financial economies: Big firms can float shares in the market for capital expansion, while small firms cannot do so.
• Managerial economies: Large scale production facilitates specialization and delegation.
• Labour economies: Large scale production implies greater and minute division of labour. This leads to specialization which enhances the quality. This increases the productivity of the firm.
• Marketing economies: The producers can both buy raw-materials in bulk at a cheaper cost and can take the products to distant markets.
• Economies of survival: Product diversification is possible and it reduces the risk in production. Even if the market for one product collapses, the market for other commodities offsets it.

Question 39.
External economies of scale:
Answer:
External economies of scale refer to changes in any factor outside the firm or industry causing an improvement in the production process.
Important external economies are:

1. Increased transport facilities.
2. Banking facilities
3. Development of townships
4. Development of information and communication

Samacheer Kalvi 11th Economics Production Analysis Additional Questions and Answers

Question 1.
Production refers to …………………….
(a) Destruction of utility
(b) Creation of utilities
(c) Exchange value
(d) None
Answer:
(b) Creation of utilities

Question 2.
_______ is a person who combines the factors of production in the production process to earn a profit.
(a) Producer
(b) Entrepreneur
(c) Consumer
(d) Labours
Answer:
(b) Entrepreneur

Question 3.
Division of labour is introduced by ………………………
(a) Adam Smith
(b) Marshall
(c) Schumpeter
(d) Hawley
Answer:
(a) Adam Smith

Question 4.
Total product is
(a) TP = ∑AP
(b) TP = ∑MP
(c) TP = ∆N
(d) TP = TP / N
Answer:
(b) TP = ∑MP

Question 5.
The Initial supply price of land is ……………………..
(a) Zero
(b) Greater than one
(c) Less than one
(d) Equal to one
Answer:
(a) Zero

Question 6.
Cobb – Douglas production function depends on ______
(a) Land, Labour
(b) Land, Capital
(c) Labour, capital
(d) Labour, organisation
Answer:
(c) Labour, capital

Question 7.
Who is the primary factor of production?
(a) Organizer
(b) Capital
(c) Machine
(d) Man
Answer:
(a) Organizer

Question 8.
_______ is the man-made factor of production.
(a) Labour
(b) Capital
(c) Savings
(d) Land
Answer:
(c) Savings

Question 9.
The technological relationship between inputs and output is called ……………………….
(a) Production function
(b) Technical function
(c) Capital function
(d) Organiser function
Answer:
(a) Production function

Question 10.
In the production process _______ bears uncertainty.
(a) Manager
(b) Labour
(c) Entrepreneur
(d) None
Answer:
(c) Entrepreneur

Question 11.
α + β = 1 refers _______
(a) Increasing returns to scale
(b) Constant return to scale
(c) Diminishing returns to scale
(d) None
Answer:
(b) Constant return to scale

Choose the correct statement

Question 1.
(a) Production refers to the creation of utility
(b) Production means the transformation of inputs into output
(c) Production creates economic well-being.
(d) The scale of production influences the revenue.
Answer:
(d) The scale of production influences the revenue.

Question 2.
(a) An entrepreneur is a risk-taker – Walker.
(b) Capital consists of all kinds of wealth other than the free gift of nature -Marshall.
(c) An entrepreneur innovates – Schumpeter.
(d) An entrepreneur is an uncertainty bearer – Walker.
Answer:
a. An entrepreneur is a risk-taker – Walker.

Match the following and choose the answer using the codes given below

Question 3.

a. 3 4 1 2
b. 1 2 3 4
c. 4 1 2 3
d. 2 1 3 4
Answer:
(c) Active factor – (3) Cobb-Douglas

Question 4.

a. 2 4 1 3
b. 1 2 3 4
c. 3 4 1 2
d. 4 1 2 3
Answer:
(a) (α + β) =1 – (1) Diminishing returns.

Question 5.

Answer:
a. 1 2 3 4
b. 4 1 2 3
c. 3 1 2 4
d. 2 3 1 4
Answer:
(c) Perfectly inelastic supply = (3) Es < 1

Question 6.

a. 2 3 1 4
b. 3 4 1 2
c. 4 1 2 3
d. 3 4 2 1
Answer:
(b) Labour = (2) Initiator

Choose the odd one out

Question 7.
(a) Land
(b) Labour
(c) Production
(d) Organisation
Answer:
(c) Production

Question 8.
(a) Technical economics
(b) Financial economics
(c) Economics of survival
(d) Banking facility
Answer:
(d) Banking facility

Choose the correct statement

Question 9.
(a) Iso-quant has a positive slope.
(b) Iso-quants never intersect each other
(c) Iso-quants are concave to the origin
(d) Iso-quant curve touch either X or Y-axis.
Answer:
(b) Iso-quants never intersect each other

Question 10.
Cobb-Douglas production function.
(a) Implies constant returns to scale
(b) It considers all the factors of production.
(c) The elasticity of substitution between the factors is less than one.
(d) Is a non-linear homogeneous production function.
Answer:
(a) Implies constant returns to scale

Analyze the reason for the following 

Question 11.
Assertion (A): Labour is the human input into the production process.
Reason (R): Labour cannot be separated from the labourer.
a. Both (A) and (R) are true, (R) is the correct explanation of (A)
b. Both (A) and (R) are true, (R) is not the correct explanation of (A)
c. Both (A) and (R) are false.
d. (A) is true but, (R) is false.
Answer:
b. Both (A) and (R) are true, (R) is not the correct explanation of (A)

Question 12.
Assertion (A) : Perishables have a low elasticity of supply.
Reason (R) : Perishables cannot be stored for a long time.
a. Both (A) and (R) are true, (R) is the correct explanation of (A)
b. Both (A) and (R) are true, (R) is not the correct explanation of (A)
c. (A) is true but (R) is false.
d. (A) is false but (R) is true.
Answer:
a. Both (A) and (R) are true, (R) is the correct explanation of (A)

Choose the incorrect pair

Question 13.

Answer:
(a) Q = AL^α K^β

Question 14.

Answer:
(d) Q = f (N,L,K,T)

Fill in the blanks with the suitable option given below 

Question 15.
Cobb-Douglas production function depends on _____
(a) Land, labour
(b) Land, capital
(c) Labour, capital
(d) Labour, organisation
Answer:
(c) Labour, capital

Question 16.
Total product is _____
(a) TP = ∑AP
(b) TP = ∆N
(c) TP = ∑MP
(d) TP = \(\frac { TP }{ N } \)
Answer:
(c) TP = ∑MP

Question 17.
In the production process __________ bears uncertainty.
(a) Manager
(b) Labour
(c) Worker
(d) Entrepreneur
Answer:
(d) Entrepreneur

Choose the best option 

Question 18.
is the man-made factor of production.
(a) Labour
(b) Capital
(c) Savings
(d) Land
Answer:
(b) Capital

Question 19.
The labour exercised without expecting income is __________
(a) Service
(b) Physical labour
(c) Mental labour
(d) None of the above
Answer:
(a) Service

Question 20.
Marginal product is ________
(a) MP = \(\frac { AP }{ N } \)
(b) MP = \(\frac { TP }{ N } \)
(c) MP = \(\frac { ∆AP }{ ∆N } \)
(d) MP = \(\frac { ∆TP }{ ∆N } \)
Answer:
(d) MP = \(\frac { ∆TP }{ ∆N } \)

Part – B

Answer the following questions in one or two sentences

Question 1.
What are the characteristics of capital?
Answer:

1. Capital is a man-made factor
2. Capital is mobile between places and persons
3. Capital is a passive factor of production
4. Capital’s supply is elastic
5. Capital’s demand is a derived demand
6. Capital is durable

Question 2.
What is the land?
Answer:
Land means all gifts of nature owned and controlled by human beings which yield an income.

Question 3.
Explain the law of variable proportions assumptions?
Answer:

1. The Law of Variable Proportions is based on the following assumptions.
2. Only one factor is variable while others are held constant.
3. All units of the variable factor are homogeneous.
4. The product is measured in physical units.
5. There is no change in the state of technology.
6. There is no change in the price of the product.

Question 4.
What is the total product?
Answer:
Total product is the summation of marginal products.
TP = ∑MP

Question 5.
What is the average product?
Answer:
Average product refers to the output per unit of the input.

Question 6.
What are diseconomies of scale?
Answer:
Diseconomies of scale are a disadvantage to a firm or industry or organization. This necessarily increases the cost of production.

Question 7.
What are Iso-quants?
Answer:
An Iso-quant curve can be defined as the locus of points representing various combinations of two inputs yielding the same output.

Part – C

Answer the following questions in One Paragraph

Question 1.
State the characteristics of labour.
Answer:

1. Labour is an active factor of production.
2. Labour may be manual or intellectual.
3. Labour is perishable.
4. Labour is inseparable from the labourer.
5. Labour is less mobile.
6. Labour is a means as well as an end.
7. Labour units are heterogeneous.
8. Labour has weak bargaining power.

Question 2.
Define Iso – quant, and Iso – quants Assumptions?
Answer:
Definition of Iso – quant:
According to Ferguson, “An Iso – quant is a curve showing all possible combinations of inputs physically capable of producing a given level of output”.

Assumptions:

1. It is assumed that only two factors are used to produce a commodity.
2. Factors of production can be divided into small parts.
3. The technique of production is constant.
4. The substitution between the two factors is technically possible. That is, the production function is of a “variable proportion” type rather than a fixed proportion.
5. Under the given technique, factors of production can be used with maximum efficiency.

Question 3.
Who is an entrepreneur?
Answer:
An entrepreneur is a person who combines land, labour, and capital in the production process to earn a profit. He not only runs the business but bears the risk of the business.

Question 4.
Differentiate the short period and long period.
Answer:
The short-run is the period where some inputs are variable. Another feature is that firms do not enter or exit the industry. The long-run is the period where all the inputs are variable. It is featured by the entry of new firms and the exit of existing firms from the industry.

Question 5.
Name the classification of a production function.
Answer:
Production function may be classified into two.

1. Short-run production function as illustrated by the law of variable proportions.
2. Long-run production function as explained by the laws of returns to scale.

Question 6.
What is an Iso-quant map?
Answer:
An Iso-quant map has different Iso-quant curves representing the different combinations of factors of production, yielding the different levels of output. An Iso-quant map is a family of Iso-quants.

Part – D

Answer the following questions in about a page

Question 1.
What are the characteristics of labour?
Answer:

1. Labour is the animate factor of production.
2. Labour is an active factor of production.
3. Labour implies several types: It may be manual [farmer] or intellectual [teacher, lawyer, etc]
4. Labour is perishable.
5. Labour is inseparable from the labourer.
6. Labour is less mobile between places and occupations.
7. Labour is a means as well as an end. It is both the cause of production and the consumer of the product.
8. Labour units are heterogeneous.
9. Labour differs inability.
10. Labour – supply determines its reward [wage]
11. Labour has weak bargaining power.

Question 2.
Explain the law of supply with a diagram.
Answer:
1. Law of supply:
The Law of supply describes a direct relationship between the price of a good and the supply of that good.

2. Definition:
“Other things remaining the same, if the price of a commodity increases its quantity supplied increases and if the price of a commodity decreases, quantity supplied also decreases”.

3. Supply function:
Q = f (P_x, P_r, P_r T, O, E)
Q_s – Quantity supplied of x commodity
P_x – Price of x commodity
P_r – Price of related goods
P_f – Price of factors of production.
T – Technology
O – Objective of the producer.
E – The expected price of the commodity

Assumptions:

1. There is no change in the prices of factors of production and capital goods.
2. Natural resources, technology, climate, political situations, and tax policy remain unchanged.
3. Prices of substitutes are constant.

Supply schedule:
A supply schedule shows the different quantities of supply at different prices

Supply curve:
The quantum supplied is represented on X-axis. And the price of the commodity is represented on the Y-axis

As the price of the commodity increases, the quantum supplied of the commodity also increases. Thus the supply curve has a positive slope. The points such as e, d, c, b, and a on the supply curve SS, represent various quantities of different prices.

Question 3.
Explain the factors determining supply.
Answer:
1. Price of the commodity:
The higher the price larger the supply Price is the incentive for the producers and sellers to supply more.

2. Price of other commodities:
The supply of a commodity not only depends upon its price but also the prices of other commodities. For instance, if the price of commercial crops increases, the supply of food crops may decrease.

3. Price of factors:
When the input prices go up, this results in rising in cost and so supply will be affected.

4. Price expectations:
The expectation over future prices determines present supply.

5. Technology:
With the advancement in technology, production level improves average cost declines, and as a result supply level increases.

6. Natural factors:
In agriculture, natural factors like a monsoon, climate, etc., play a vital role in determining the production level.

7. Discovery of new raw materials:
The discovery of cheaper and high-quality raw materials tends to increase the supply of the product.

8. Taxes and subsidies:
Subsidies encourage the producers to produce more whereas taxes kill the ability and willingness to produce more.

9. The objective of the firm:
When the goal of the firm is sales maximization or improving market share, the supply of the product is likely to be higher.

Question 4.
Explain the characteristics of labour.
Answer:
According to Marshall, labour represents services provided by the factor labour, which helps in yielding an income to the owner of the labor-power.
Characteristics of labour:

1. Labour is the animate factor of production.
2. Labour is an active factor of production.
3. Labour implies several types it may be manual or intellectual.
4. Labour is perishable.
5. Labour is inseparable from the labourer.
6. Labour is less mobile between places and occupations.
7. Labour is a means as well as an end.
8. Labour units are heterogeneous.
9. Labour-supply determines its reward.
10. Labour has weak bargaining power.

Students can Download Commerce Chapter 28 Balance of Trade and Balance of Payments Questions and Answers, Notes Pdf, Samacheer Kalvi 11th Commerce Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Samacheer Kalvi 11th Commerce Solutions Chapter 28 Balance of Trade and Balance of Payments

Samacheer Kalvi 11th Commerce Balance of Trade and Balance of Payments Textbook Exercise Questions and Answers

I. Choose the Correct Answer

Question 1.
The Statement which discloses a record of transactions between the residents of one country and residents of foreign country …………….
(a) Balance of Payment
(b) Balance of Trade
(c) Statement of Receipts and Payments
(d) Accounting Statement
Answer:
(a) Balance of Payment

Question 2.
The Balance of Payments councils consists of …………….
(a) Current Account
(b) Capital Account
(c) Receipts and Payments Account
(d) Both Current Account and Capital Account
Answer:
(d) Both Current Account and Capital Account

Question 3.
Foreign capital long – term loan and foreign currency reserve are recorded under …………….
(a) Official Capital
(b) Private Capital
(c) Banking Capital
(d) Both Private and Official Capital
Answer:
(b) Private Capital

Question 4.
The term official capital includes …………….
(a) RBI holdings of foreign currencies
(b) Special Drawing Rights held by the Government
(c) Both A and B
(d) Foreign Investment
Answer:
(c) Both A and B

Question 5.
Balance of payments surplus indicates …………….
(a) Exports are more than the Imports
(b) Imports are more than Exports
(c) Exports and Imports are at Equilibrium
(d) Exports and Imports are above Equilibrium
Answer:
(a) Exports are more than the Imports

II. Very Short Answer Questions

Question 1.
What do you mean by Balance of payments?
Answer:
Balance of payment refers to a systematic record of all economic transactions between the residents of one country and the residents of foreign countries during a particular period of time. For example, one year.

Question 2.
What do you mean by Balance of trade?
Answer:
Balance of trade denotes the difference between the value of import and the value of export during a year.

Question 3.
Define the Balance of payments.
Answer:
According to International Monetary Fund, “The balance of payments for a given period is a systematic record of all economic transactions taken place during the period between residents of the reporting countries.”

Question 4.
What is the composition of private capital?
Answer:
Private capital consists of foreign investments, long-term loan,s and foreign currency deposits.

Question 5.
Mention the components of banking capital.
Answer:
Banking capital includes movement into external financial assets and liabilities commercial and co-operative banks authorized to dealing in foreign exchange.

Question 6.
Mention the components of official capital.
Answer:
It includes RBI’s holdings of foreign currency and special drawing rights (SDR) held by the Government.

III. Short Answer Questions

Question 1.
Why is the Balance of payment prepared?
Answer:
Balance of payment is the principal tool for analyzing the monetary position of international trade of a country just like Receipts and Payments account of enterprise revealing the net effect of cash movements happening in an enterprise during a particular period.

Balance of payments help in framing monetary, fiscal, and trade policies of the country. It reveals whether a country produces enough economic output to pay for its growth. It is reported either for every quarter or for a year.

Question 2.
What does the Balance of payment disclose?
Answer:
A Balance of Payment surplus indicates that country’s exports are more than its imports and its government and residents are savers. A Balance of Payment deficit points to the fact that the country’s import is more than the export. This situation forces the country to borrow from other countries to pay for its imports.

Question 3.
What are the credit items shown in currents accounts?
Answer:
In the current account the following credit items have been shown:
1. Goods Export(visible)
2. Invisible-Exports

• Transport service sold abroad
• Banking service sold abroad
• Insurance service sold abroad
• Income received on loan and investments made in foreign countries.
• Expenses incurred by foreign tourists in India

Question 4.
State the components of capital account.
Answer:
Capital account consists of three components

1. Private Capital
2. Banking Capital
3. Official Capital

IV. Long Answer Questions

Question 1.
Write down the structure of the capital account.
Answer:
The capital account consists of three components

1. Private Capital: Private capital consists of foreign investments, long term loan, and foreign currency deposits
2. Banking Capital: Banking capital includes movement into external financial assets and liabilities commercial and co-operative banks authorized to dealing in foreign exchange.
3. Official Capital: It includes RBI’s holdings of foreign currency and special drawing rights (SDR) held by the Government.

Question 2.
Distinguish balance of payment and balance of trade.
Answer:

Question 3.
Highlight the features of the balance of trade.
Answer:
Meaning: Balance of Trade denotes the difference between the value of import and the value of export during a year.

Features of Balance of Trade:

• It is a statement showing the net effect of the export and import of a country.
• It records only transactions relating to merchandise.
• It does not record capital transactions
• It is a part of the current account of Balance of Payment.
• It may be at favourable or unfavourable or in an equilibrium state.
• It is not the true indicator of economic prosperity or economic relations of a country.
• Unfavourable balance of trade can be converted into favourable balance of payment.

For Future Learning

Question a.
Impact of Balance of Payments and Trade.
Answer:
The global village is also a term to express the constituting relationship between economics and other social sciences throughout the world making it a part of our popular culture before it actually happened.

Question b.
Necessary for Global Village concept.
Answer:
The current account, capital account, and financial account together make up the overall balance of payments, which accounts for all of the international inflows and outflows for a given Nation. The current account, as mentioned, capture the balance of trade meaning the purchases and sale of goods and services.

For Own Thinking

Question a.
Balance of Payment is key to economic development.
Answer:
Yes, it is correct.

Question b.
Importance of BOP and BOT.
Answer:
BOP:

1. It presents the international financial positions of the country.
2. It helps the government in taking decisions on monetary and fiscal policies on the one hand and on external trade and payments issued on the other.

BOT:

1. It is the difference between a country’s imports and export over a period of time.
2. It is the largest component of the balance of payments for all nations.

Students can Download English Lesson 5 The Singing Lesson Questions and Answers, Summary, Activity, Notes, Samacheer Kalvi 11th English Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations. Learn the Samacheer Kalvi 11th English Grammar to enhance your grammar skills like reading comprehension, passage writing, parts of speech, tenses, passive and active voice, and many other concepts in no time.

Tamilnadu Samacheer Kalvi 11th English Solutions Supplementary Chapter 5 The Singing Lesson

Warm up

Question 1.
What are all the factors that influence our moods?
Human beings are bundles of emotions, A small angry look from a friend, a scolding from a teacher one admires, a taunt from mom could influence our moods the whole day.

Question 2.
How do you behave under the spells of different moods?
Answer:
When good things keep happening, we are happy. If we don’t get an easy question paper or the expected questions don’t appear we feel quite upset. If a close friend becomes angry, instead of analysing what caused it, we feel dejected. When centum is the goal, even 99% of marks disappoints us.

Question 3.
Do you think it is important not to be swayed by every passing mood?
Answer:
Yes, we should not be swayed by every passing emotions. But we are the sum total of our experiences. What ever bitter sweet experiences that occur do influence us. Latest researches . say that the food we eat, weather, clothes, the colour around us and punishing work schedules can adversely affect our moods. It would be ideal if we don’t allow external circumstances to influence our equanimity of mind and the ability to stay focused on our goals.

Question 4.
Suggest some ways by which we can maintain a calm temperament under all circumstances.
Answer:
Early morning walks, meditation and the practice of treating both success and failure, joy and sorrow with the same composure will naturally increase our life span on this planet. Listening to good music and reading good books, not only text books, can drastically reduce unpleasant stress. Thus we can maintain a calm temperament at all occasions.

Samacheer Kalvi 11th English The Singing Lesson Textual Questions

A. Based on your understanding of the story, answer the following questions in about 30 – 50 words each.

Question 1.
What was the knife that Miss Meadows carried with her?
Answer:
Miss. Meadows had received a letter from Mr. Basil calling off the marriage. She deemed it a kind of personal failure. Her anger and disappointed became despair. She carried cold despair buried deep in her heart like a wicked knife.

Question 2.
What kind of relationship existed between Miss Meadows and the Science Mistress?
Answer:
Both hated each other. Science Miss gave her a “Sugary smile” concealing her hostility. But Miss. Meadows enquiries responded to her deception always with a cold grimace.

Question 3.
Why was Miss Meadows upset and dejected?
Answer:
Mr. Basil had written a disquieting letter after his engagement with her. He had claimed that he was not a “Marrying man”. The thought of marriage gave him a feeling of disgust. He had struck out the word disgust and replaced it with ‘regret’ to lessen the hurt. So, Miss. Meadows was upset and dejected.

Question 4.
How would Miss Meadows usually treat Mary? How did her behaviour towards the girl change that day?
Answer:
Usually she would receive the flower from her favourite pupil Mary Beazley. She would tuck it in her belt with great tenderness and give a smile to her. The music class would start with a joyful note.

Question 5.
Why had Miss Meadows chosen ‘A Lament’ as the lesson that particular day?
Answer:
Miss. Meadows had chosen “A lament” as a lesson for that particular day. She was only in a mood to lament her broken engagement and shattered dreams. The choice of the music lesson reflected her real mood of dejection and despondency.

Question 6.
What brought agony to the girls during the music lessons?
Answer:
During the music lesson, Miss. Meadows did not show any warmth. She was icy cold and mechanical in her instructions. Children could easily realize that Miss. Meadow was in a wax. Miss. Meadow totally ignored the chrysanthemum from her favourite pupil. She also did not respond to her greeting. This sent tremors across the class. Young ones quickly understood the unstated message that music Miss was in one of her worst moods confirming their guess, she gave them “a lament” to practice.

The lesson was devoid of any warmth and joy. The lyrics of the song was so gloomy that children entered the world of unnatural agony and despair.

Question 7.
Bring out the substance of Basil’s letter to Miss Meadows.
Answer:
The content of Basil’s letter read, “I feel more and more strongly that our marriage would be a mistake. Not that I don’t love you. I love you as much as it is possible for me to love any woman but, truth to tell, I have come to the conclusion that I am not a marrying man and the idea of settling down fills me with nothing but – the word “disgust” was scratched out and “regret” written over the top.

Question 8.
Why did Miss. Wyatt summon Miss. Meadows to her room?
Answer:
A telegram addressed to Miss. Meadows was received at the school’s office. The Head mistress could not fathom the content of the Telegram. Believing that the telegram must be a harbinger of a tragedy, the Headniistress Miss. Wyatt summoned Miss. Meadows to her room.

Question 9.
How did Miss. Meadows express her joy, when she returned to the music class?
Answer:
Miss. Meadows changed the song for the children. She asked them to sing a joyful song beginning with flowers o’er laden. When she found that some children were still stuck up in the despondent mood, she reprimanded them. She told the girls, don’t look so doleful. It ought to sound warm, joyful and eager. And this time Miss. Meadow’s voice dominated the voices of all the little angels in her classroom. It was deep and glowing with a cheerful expression.

Question 10.
Briefly explain the cause of Miss Meadows’ joy at the end.
Answer:
Contrary to the expectation of Miss. Wyatt, the telegram was from Basil. It was an apology and reconciliatory in nature. In the telegram, her fiance had asked her to ignore the letter written when he must have been mad. A few hours before, she was the embodiment of disappointment and self-pity. The telegram had restored her joy. She could gather the pieces of her shattered dreams and hopes and built them anew. She was so happy that Miss. Wyatt’s warnings fell into deaf ears.

Vocabulary

A. Note the following words from the story. They all refer to different ways of walking. Find out their meanings and use each of them in meaningful sentences of your own. Refer a thesaurus and add a few more to the list.

(a) trod (b) fluttered (c) hurried (d) skipped (e) strode (f) sped

(a) trod – walked, stepped, strode, went
(b) fluttered – hovered, danced, flitted, flapped, oscillated, twitched, vibrated, flickered
(c) hurried – went fast, hastened, sped, charged, sprinted, chased, scampered, galloped, scrambled.
(d) skipped – capered, bobbed, bounded, jumped, leapt, gambolled,’frisked, romped
(e) strode – marched, trod, paced, stalked, dashed, ran, flaunted, joggled, tramped, rushed,zoomed
(f) sped – hurried, rushed, zipped, spurred, hurtled, sailed, hastened, quickened

B. Complete the mind map given below and write a brief summary of the story in your own words.

Answer:

(i) a letter from Basil breaking the engagement
(ii) irritable
(iii) sing a lament
(iv) Basil as a knife piercing her heart
(v) deserted her
(vi) of mpod
(vii) Head mistress Miss. Wyatt
(viii) the letter

A brief summary:
Miss Meadows was upset over a letter from Basil breaking the engagement. She remains gloomy and irritable in class. She taxes the students making them sing a lament. She thinks of the letter from Basil as a knife piercing her heart. Basil seems to have deserted her. Suddenly she is called by Head mistress Miss. Wyatt. The headmistress gives her a telegram which asks her to forget the letter. Miss Meadows feels happy and returns to the class with vigour and good cheer.

C. Answer the following questions in a paragraph of about 150 words each.

Question 1.
Describe Miss Meadows’ mood before and after receiving the telegram. How did it affect her class?
Answer:
A despairing singing teacher, Miss Meadow has to start her class, but she has just received a letter from her fiance, Basil This letter makes her that their relationship was ended. As she entered the class, she doesn’t answer the girl’s greeting. Mary’s eyes get filled with tears. The teacher orders the girls to sing a ‘lament.

They sing with ‘mournful voices. The teacher contaminates them with her state of spirit. Soon a telegram -from Basil was sent to Miss Meadows, asking her to apologize him. The teacher comes back to the class smiling and asks the students to sing another song, happy and sweet without explanations as if nothing had happened.

Question 2.
‘The only difference between a good day and a bad day is your attitude.’Relate this to a real life experience you have had. Share your thoughts in class.
Answer:
It is true that attitude makes or mars things. I was waiting for my Std X public exam resuls. I had put in 10 hours of work everyday. I was an average boy but I hoped to join the top five any time. The results were scheduled to be out the next morning. I have no internet connectivity at home. But one of my friends had it. His name is Murali. His father had come to my home. When I was out, he had told my parents I had failed in one subject. When I returned home, I found both my parents upset. I asked them what was wrong. They said it was a bad day. I asked them to tell me what was in their mind. They asked me to take things as they come by.

I didn’t understand. My dad told philosophically that failure is a stepping stone to success. Still they were not open with me. When I went out for tea, the local newspapers carried Std X public exam results. To my joy, I had passed with a first class. When I broke the news, my parents disclosed what had upset them. If they had just not reacted to the wrong information, their natural joy would not have been robbed. Now that they knew the information, they were over joyed. I just wondered at the human capacity to go down in misery and bounce back to extreme joy just by a turn of events. The best course of action to be happy all the time would be to. retain the key to our happiness and never give up on our joy to any external event.

“Don’t take it on yourself to repay a wrong. Trust the Lord and He will make it right.”

Question 3.
You are busy getting ready for school. You receive a WhatsApp message from your best friend, saying that he/she is very upset over the fight you had yesterday and doesn’t want to talk to you anymore. This distresses you as she sounds very firm. However, today is a big day at school with two tests lined up. What will be your state of mind? How will you handle this situation?
Answer:
My best friend is my soul mate If he/she fought with me I couldn’t concentrate on my work peacefully I will give more importance to my friends as my family. If we got misunderstanding surely the day will be the worst day for me. Because I can’t be happy without my friend One day, I had a misunderstanding with my friend. The very next day, there were two tests in my school.

My mind was totally blank. I couldn’t remember a sentence to write. I kept on thinking about the fighting which was unforgettable. Even, very known answers were not written properly I tried to overcome my emotions. At last, I decided to reconcile with my friend by taking him/her to an ice cream parlour. However, I did my tests very well.

Additional Question

Question 1.
Attempt a character sketch of Miss. Meadows.
Answer:
Miss. Meadows is a 30-year-old lady. Mr. Basil a 25-year-old young man gets engaged to her. When she is cherishing the dreams of a happy married life, a letter lands on her heart like a bombshell. It shatters her dreams. It pierces her heart. Being a sensitive lady, she feels her heart is bleeding. The contents of the letter keep haunting her memory. She is unable to focus in her music classes. The miraculous engagement was almost broken. The words, “our marriage could be a mistake” leaves her bleeding. She interpreted the scornful glance of science miss . as if she had known about the “break”. He had mentioned that he was not a marrying man”.

She wondered how she would react to the disclosure of the shattered engagement to the colleagues and the villagers. She even harboured the idea of leaving her job and go into hiding somewhere. As she is in a glooming mood, she doesn’t respond to the offer of chrysanthemum with a warm smile and thanks. She gives a ‘lament’ for practice. It is only when she receives a telegram of apology from her fiance her mood gets lifted. She flits on the wings of hope and sings a joyous song along with her students. She is a perfect example of ordinary mortals who are early hurt and quickly bounce back to a hopeful life as well.

“Please don’t expect me to always be good, kind, and loving. There are times when I will be cold, thoughtless, and hard to understand.”

Additional Questions

I. Answer the following choices from the options given below.

Question 1.
Miss. Meadows hugging the __________ stared in hatred at the science mistress.
(a) baton
(b) books
(c) bite
(d) knife
Answer:
(d) knife

Question 2.
Everything about Miss. Meadows was sweet, pale like __________
(a) money
(b) honey
(c) flower
(d) rose
Answer:
(b) honey

Question 3.
Science mistress was good at showing a __________ smile whenever she came across Miss. Meadows.
(a) honey
(b) sugary
(c) feigned
(d) deceptive
Answer:
(b) sugary

Question 4.
The story is set in __________ season.
(a) winter
(b) spring
(c) autumn
(d) rainy
Answer:
(c) autumn

Question 5.
One could witness an excitement in the school __________
(a) drowsy
(b) insipid
(c) gleeful
(d) sensational
Answer:
(c) gleeful

Question 6.
Every day the presentation of a beautiful flower to Miss. Meadows by __________ her favourite has pupil become a ritual.
(a) Muriel
(b) Mr. Basil
(c) Rosy
(d) Mary Beazley
Answer:
(d) Mary Beazley

Question 7.
The little children in the music were thinking __________ is in a wax.
(a) Rowdy
(b) Meady
(c) Rosy
(d) Miss. Wyatt
Answer:
(b) Meady

Question 8.
The letter from Mr. Basil had __________ Miss. Meadows’s heart.
(a) gladdened
(b) soothed
(c) pierced
(d) embalmed
Answer:
(c) pierced

Question 9.
Mary’s __________ was totally ignored by Miss. Meadows.
(a) Rose
(b) Lilly
(c) Chrysanthemum
(d) apple
Answer:
(c) Chrysanthemum

Question 10.
The song chosen for practice in the music class was a __________
(a) love song
(b) lament
(c) joyous song
(d) hymn
Answer:
(b) lament

Question 11.
The rejection of the flower was a __________ moment in Mary Beazley’S school life.
(a) memorable
(b) unforgettable
(c) staggering
(d) astonishing
Answer:
(c) staggering

Question 12.
Nothing could be more __________ than the lament.
(a) important.
(b) beautiful
(c) tragic
(d) fabulous
Answer:
(c) tragic

Question 13.
The last time Mr. Basil had come to see Miss. Meadow, he had worn a __________ in his buttonhole.
(a) diamond
(b) pearl
(c) rose
(d) chrysanthemum
Answer:
(c) rose

Question 14.
Mr. Basil could not refuse the headmaster’s wife’s invitation for a __________ because he couldn’t afford to be unpopular.
(a) party
(b) lecture
(c) card game
(d) dinner
Answer:
(d) dinner

Question 15.
Basil had written to Miss. Meadows that their marriage would be a __________
(a) boon
(b) mistake
(c) marvel
(d) wonder
Answer:
(b) mistake

Question 16.
Mr. Basil’s previous letter was about a __________ book-case.
(a) sandal
(b) teak
(c) neem
(d) fumed-oak
Answer:
(d) fumed-oak

Question 17.
The tiny one who clung to the lament wriggled like __________ caught on a line.
(a) dogs
(b) cats
(c) elephant
(d) fishes
Answer:
(d) fishes

Question 18.
Miss. Meadows compliment with a strange, stony tone positively __________ the younger girls.
(a) encouraged
(b) boosted
(c) frightened
(d) pleased
Answer:

Question 19.
Miss. Meadows went on recalling the struck out word __________ in his letter.
(a) ‘pale’
(b) ‘white’
(c) ‘pleasing’
(d) ‘disgust’
Answer:
(d) ‘disgust’

Question 20.
Miss __________ was the school headmistress.
(a) Glory
(b) Mary
(c) Victoria
(d) Wyatt
Answer:
(d) Wyatt

Question 21.
Mrs. Wyatt really hoped for news about a __________ through the telegram.
(a) marriage
(b) tragedy
(c) comedy
(d) practical joke
Answer:
(b) tragedy

Question 22.
Miss. Wyatt had sent for Miss. Meadow because __________ a had been received at the school office.
(a) letter
(b) money order
(c) book parcel
(d) telegram
Answer:
(d) telegram

Question 23.
On hearing the news of a telegram Miss. Meadows thought that __________ must have I committed suicide.
(a) Ryan
(b) Mary
(c) Mr. Basil
(d) Osborne
Answer:
(c) Mr. Basil

Question 24.
The telegram received the stress of Miss. Meadows but added to that of Miss __________
(a) Rose
(b) Beadle
(c) Mary
(d) Wyatt
Answer:
(d) Wyatt

Question 25.
Miss. Meadows had to struggle to lift the little girl from __________ spirit to a cheerful mood.
(a) doleful
(b) hateful
(c) disdainful
(d) cheerful
Answer:
(a) doleful

Question 26.
In order to indicate that she was her normal self again she took the __________ and held it to her lips.
(a) baton
(b) knife
(e) book
(d) chrysanthemum
Answer:
(d) chrysanthemum

Question 27.
The song after receiving the telegram sounded __________ , joyful and eager.
(a) cold
(b) distasteful
(c) mournful
(d) warm
Answer:
(d) warm

Question 28.
The fateful letter made Miss. Meadows even think of __________ her job and go into hiding.
(a) taking
(b) building
(c) resigning
(d) upscaling
Answer:
(c) resigning

Question 29.
After her brief visit to Miss. Wyatt’s room dominated the students and it was glowing with __________
(a) pain
(b) bliss
(c) expression
(d) depression
Answer:
(c) expression

Question 30.
Miss Wyatt learned that the telegram was from Miss. Meadows’ __________
(a) dad
(b) fiance
(c) brother
(d) correspondent
Answer:
(b) fiance

II. Rearrange the sentences

Question 1.
(a) She did not say thanks with warmth to her favourite pupil for the flower.
(b) Most of the children realized with alarm that Miss. Meady was in a wax.
(c) Miss. Meadows looked dejected.
(d) Meadows, responding with a grimace went away and started her music.
(e) Science mistress greeted her with a sugary smile.
Answers:
(c) Miss. Meadows looked dejected.
(e) Science mistress greeted her with a sugary smile.
(d) Meadows, responding with a grimace went away and started her music.
(a) She did not say thanks with warmth to her favourite pupil for the flower
(b) Most of the children realized with alarm that Miss. Meady was in a wax.

Question 2.
(a) She was called to Miss. Wyatt’s room and given a telegram.
(b) Miss. Meadows, reflecting her despair, asked the children to sing “a lament”
(c) Miss. Meadows was upset over her fiance’s letter calling off the marriage
(d) After seeing the contents of the telegram, Miss. Meadows almost flew back to her class on the wings of hope and gave the class a joyful song to sing.
(e) Basil seemed to have deserted her.
Answers:
(c) Miss. Meadows was upset over her fiance’s letter calling off the marriage
(e) Basil seemed to have deserted her.
(b) Miss. Meadows, reflecting her despair, asked the children to sing “a lament”
(a) She was called to Miss. Wyatt’s room and given a telegram.
(d) After seeing the contents of the telegram, Miss. Meadows almost flew back to her class on the wings of hope and gave the class a joyful song to sing.

III. Identify the speaker

1. “Isn’t it cold? It might be winter” – science mistress to Miss. Meadows
2. “It is rather sharp – Miss Meadows to science mistress
3. You look frozen – Science mistress to Miss. Meadows
4. Oh! not quite as bad as that – Miss. Meadows to science mistress
5. ‘sh – sh! gives’ – Mary Beazley to fellow students
6. Silence, please! Immediately” – Miss Meadows to her student
7. “Good morning Miss. Meadows” – Mary Beasley to music miss
8. “Thank you Mary, How very nice! Turn to page 32” – Miss Meadows to Mary Beasley
9. Page fourteen, please mark the accent – Miss. Meadows to the music class children
10. What could have possessed him to write such a letter? – Monologue from Miss. Meadows
11. The third line should be one crescendo – Miss. Meadows to her class
12. “Away’ you must begin to die – to fade – until the listening ear” is nothing more than a whisper – Miss Meadows, to her music class students
13. Well, Monica, what is it? – Miss Meadows to Monica
14. Miss. Wyatt wants to see you in the mistress’s room. – Miss Monica to Miss. Meadows
15. “I shall met you in honour to talk quietly while I am away,” – Miss to her students in music class
16. “I sent for you just now because this telegram has come for you” – Miss Wyatt to Miss Meadows
17. “A telegram for me, Miss. Wyatt” – Miss Meadows to Miss Wyatt
18. “I hope it’s not bad news” – Miss Wyatt to Miss. Meadows
19. “I do hope, it’s nothing serious” – Miss Meadows to Miss Wyatt
20. Oh, no, thank you, Miss. Wyatt – Miss. Meadows to Miss Wyatt
21. You’ve fifteen minutes more of your class … Miss Meadows, haven’t you? – Miss Wyatt to Miss Meadows.
22. ”It’s from my fiance saying that… “ – Miss Meadows to Miss. Wyatt.

IV. Reading comprehension.

1. With despair – cold, sharp despair – buried deep in her heart like a wicked knife, Miss Meadows, in cap and gown and carrying a little baton, trod the cold corridors that led to the music hall. Girls of all ages, rosy from the air, and bubbling over with that gleeful excitement that comes from running to school on a fine autumn morning, hurried, skipped, fluttered by; from the hollow classrooms came quick drumming of voices; a bell rang; a voice like a bird cried, “Muriel.”

And then there came from the staircase a tremendous knock-knock-knocking. Someone had dropped her dumbbells. The Science Mistress stopped Miss Meadows. “Good morning,” she cried, in her sweet, affected drawl. “Isn’t it cold? It might be winter.” Miss Meadows, hugging the knife, stared in hatred at the Science Mistress. Everything about her was sweet, pale, like honey. You would not have been surprised to see a bee caught in the tangles of that yellow hair. “It is rather sharp,” said Miss Meadows, grimly. The other smiled her sugary smile.

Question (a)
What is a baton used for?
Answer:
A baton is a long stick used for conducting a music orchestra.

Question (b)
What was the wicked knife?
Answer:
Sharp despair was the wicked knife.

Question (c)
Why was Miss Meadows in a state of despair?
Answer:
Mr. Basic had written a letter calling off their engagement. So, Miss. Meadows was in a state of despair.

Question (d)
Why was the greeting of science mistress affected?
Science mistress did not have real feelings for Miss. Meadows. It was out of courtesy that she offered a sugary smile to Miss. Meadows and asked after the weather.

2. Forms Four, Five, and Six were assembled in the music hall. The noise was deafening. On the platform, by the piano, stood Mary Beazley, Miss Meadows’ favorite, who played accompaniments. She was turning the music stool. When she saw Miss Meadows, she gave a loud, warning “Sh-sh! Girls!” and Miss Meadows, her hands thrust in her sleeves, the baton under her arm, strode down the centre aisle, mounted the steps, turned sharply, seized the brass music stand, planted it in front of her, and gave two sharp taps with her baton for silence.

“Silence, please! Immediately!” and, looking at nobody, her glance swept over that sea of coloured flannel blouses, with bobbing pink faces and hands, quivering butterfly hair-bows, and music-books outspread. She knew perfectly well what they were thinking. “Meady is in a wax.” Well, let them think it! Her eyelids quivered; she tossed her head, defying them. What could the thoughts of those creatures matter to someone who stood there bleeding to death, pierced to the heart, by such a letter

Question (a)
Who was Miss. Meadows favourite pupil?
Answer:
Mary Beazley was Miss. Meadows’favourite pupil.

Question (b)
How did Mary alert the fellow students?
Answer:
On seeing Miss. Meadows, Mary alerted the fellow students saying,” sh – sh! girls”.

Question (c)
How did Miss. Meadows silence the music class?
Answer:
There was a brass music stand. Miss. Meadows gave two sharp taps with her baton to silence the music class.

Question (d)
According to Miss. Meadows, what were the children thinking about her on that bad day?
Answer:
Children were thinking that Miss. Meady is in a wax”.

Question (e)
What did the thoughts of children not affect Miss. Meadows?
Answer:
The letter from Mr. Basil had pierced her heart. She was bleeding to death. In such a state, Miss. Meadows could not possibly think about what the children were thinking about her.

The Singing Lesson About the Author

Kathleen Mansfield Murry (1888 – 1923) was a New Zealand short story writer who wrote under the pen-name Katherine Mansfield. She left New Zealand at the age of 19 and settled in the United Kingdom where she gained the friendship of great writers such as 0.11. Lawrence and Virginia Woolf. Bliss and The Garden Party were collections of short stories written by her. She wrote many poems and her collected letters were a great success.

The Singing Lesson Summary

This story depicts the fact that human moods are often influenced by experiences good or bad. The story revolves around the swings of mood experienced by Miss. Meadows and how it affected her work directly. Miss. Meadows, a music teacher aged 30, is engaged to 25 years old Basil. It was a huge surprise to everyone including the science teacher whom Miss. Meadows hates with all her heart. Suddenly she receives a disheartening letter from Basil that he is not a ‘marrying type of man’. The very idea of marriage gives him a feeling of “disgust”. But out of courtesy he had struck down the word disgust and written “regret”. After reading the letter Miss. Meady became gloomy. She had a feeling that her engagement was broken and it would soon come to the knowledge of everyone.

She would be a laughing stock. She will have to resign her job and go into hiding somewhere. This feeling of despair and disappointment had hurt her so much that she did not even accept the chrysanthemum from her favourite student Mary Beazley. A Chinese proverb says, “One cannot prevent. Under normal circumstances, she would have tucked the flower in her belt and returned a beaming smile to her favourite pupil. Miss. Meady made the children sing a lament creating an atmosphere of icy gloom befitting an occasion of mourning. She was very severe with young ones who didn’t evidence considerable pain and expression in her voice. Relief came to the drudgery of lament in the form of a telegram. Monica informed Miss. Meadows to meet the Headmistress. Miss. Meadows wondered if Mr. Basil had committed suicide. Her hands flew out in anxiety to collect the telegram from Miss. Wyatt.

Miss. Wyatt hoped it was bad news but out of politeness said, “I hope it is not bad news.” Miss. Meadows tore open the telegram. To her great relief it read, “Pay no attention to letter. Must have been mad, bought hat-stand today-Basil”. To answer the anxious query of Miss. Wyatt, Miss. Meadows blushed and said it was from her fiance. This happy turn of events upset Miss. Wyatt who disallowed telegrams on happy occasions. She reminded her of the 15 minutes left of her music class. Miss. Meadows ran all the way back to the music class. It appeared that she was flying on the wings of hope, love and joy. She picked up the deserted yellow chrysanthemum and held it to her lips to hide her smile.

Her mood suddenly switched over boundless joy. It reflected in the music lesson. She asked her pupils to turn to page 32 and sing the most joyous song the children had ever practised. Those who were blowing their nose from feigned sorrow and rigidity of the music, couldn’t suddenly move on to a joyful note. Miss. Meadow chided them for lack of feeling and expression.

Conclusion: The telegram restores her hopes, joy and faith in future, Many of us become prisoners of circumstances and over react to pinpricks in life. One should learn to be composed and take all kinds of information with a pinch of salt. Birds of sorrow hovering over one’s head. But one can prevent them from building nests in one’s head.

Textual:

• accompaniments – music played to support an instrument, voice or group
• aisle – a passage between rows of seats
• drawl – slow, lazy way of talking
• fiance – a man to whom one is engaged to be married
• forte – a musical tone played loudly
• grimace – expression of disgust on a person’s face of a music orchestra
• tangles – a contused mass, twisted

Additional:

• chided -rebuked
• disgust – revulsion
• disallow – refuse
• gloom – dejection
• joyful – cheerful
• joyous – happy
• lament – an expression of grief
• regret – feel sad
• relief – the feeling of relaxation from tension
• suicide – killing oneself
• upset – pained

Students can Download Commerce Chapter 27 Facilitators of International Business Questions and Answers, Notes Pdf, Samacheer Kalvi 11th Commerce Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Samacheer Kalvi 11th Commerce Solutions Chapter 27 Facilitators of International Business

Samacheer Kalvi 11th Commerce Facilitators of International Business Textbook Exercise Questions and Answers

I. Choose the Correct Answer

Question 1.
General Agreement on Tariff and Trade was signed on ………………
(a) 30 – October – 1947
(b) 29 – October – 1947
(c) 28 – October – 1947
(d) 26 – October – 1947
Answer:
(a) 30 – October – 1947

Question 2.
WTO was established on ………………
(a) 1 – 1 – 1996
(b) 1 – 1 – 1997
(c) 1 – 1 – 1995
(d) 1 – 1 – 1994
Answer:
(c) 1 – 1 – 1995

Question 3.
The headquarter of WTO is located at ………………
(a) New York
(b) London
(c) Geneva
(d) Brazil
Answer:
(c) Geneva

Question 4.
The day to day administration of WTO is entrusted with ………………
(a) Executive Council
(b) General Council
(c) Administrative Council
(d) General Body
Answer:
(b) General Council

Question 5.
World bank is located at ………………
(a) Washington DC
(b) New York
(c) Tokyo
(d) Hongkong
Answer:
(a) Washington DC

II. Very Short Answer Questions

Question 1.
What is WTO?
Answer:
The World Trade Organisation (WTO) was established on 1 st January 1995. The GATT was renamed as WTO with some changes. WTO has 164 member countries as of 29th July 2016. The ministerial conference consisting of the representatives of all the member countries is the highest decision-making authority of WTO.

Question 2.
What do you mean by World Bank?
Answer:
International Bank for Reconstruction and Development (IBRD) International Bank for Reconstruction and Development is commonly known as World Bank.

Question 3.
What are Special Drawing Rights?
Answer:
SDR was created by the IMF in the year 1969 as a supplementary international reserve asset. It is described as paper gold. Initially, the value of SDR was fixed to be 0.888671 grams of fine gold equivalent to one US dollar till the year 1973.

After the collapse of the Britten Wood system in 1973 SDR was redefined as a basket of currencies. From 1st October 2016 SDR basket consists of US dollar, Euro, the Chinese Rimini, Japanese Yen and British Pound sterling. The value of SDR is regularly posted daily in the IMF website.

Question 4.
What is SAARC?
Answer:
South Asian Association for Regional Cooperation is the regional intergovernmental organization and geopolitical union of nations in South Asia.

Question 5.
What is GATT?
Answer:
The General Agreement on Tariffs and Trade was the first worldwide multilateral free trade agreement. It was in effect from June 30, 1948, until January 1, 1995. The purpose of GATT was to eliminate harmful trade protectionism.

III. Short Answer Questions

Question 1.
What is the primary motive for the establishment of WTO?
Answer:
GATT achieved many successes but various countries felt the need to create a new international body to replace the GATT. The GATT which remained in force from 1948 to 1994 thus came to an end with the establishment of the World Trade Organisation (WTO) on 1st January 1995.

Question 2.
Name the affiliate of World Bank.
Answer:
The following are the affiliates of the world bank.

• International Development Association
• International Financial Corporation
• Multinational Investment Guarantee Agency
• International Centre for Settlement of Investment Disputes

Question 3.
What are the criticisms of the World Bank?
Answer:

1. Free Trade Benefits Developed Countries more than Developing Countries
2. Most Favoured Nation Principles
3. Failure to Reduce Tariffs on Agriculture
4. Neglect of Farmers Interest in Developing Countries
5. Neglect Environmental Considerations
6. Neglect of Cultural and Social Factors
7. The inability of People in Developing Countries to Buy Life Saving Drugs

Question 4.
How is the value of SDR determined currently?
Answer:
It is calculated as the sum of a specific amount of each basket currency value in US dollar based on the spot exchange rates observed at noon London time. IMF allocates SDR to member countries in proportion to their quota.

Question 5.
Mention the functions of SAARC.
Answer:

1. Monitoring and coordinating the development program
2. Determining inter-sectoral priorities
3. Mobilizing cooperation within and outside the region.
4. Dealing with modalities of financing

IV. Long Answer Questions

Question 1.
Point out the objectives of WTO.
Answer:
Meaning: The World Trade Organisation (WTO) was established on 1st January 1995. The GATT was renamed as WTO with some changes. WTO has 164 member countries as of 29th July 2016. The ministerial conference consisting of the representatives of all the member countries is the highest decision-making authority of WTO The objectives of WTO include the following.

• Improving the standard of living of people in member countries
• Making optimum utilization of the world’s resources for sustainable development of member countries.
• Promoting an integrated more viable and durable trading system in the sphere of international business
• Expansion of trade in goods and services
• Ensuring full employment and large steady growth volume of real income and effective demand
• Protecting the environment.

Question 2.
Write down the functions of WTO.
Answer:

1. It is a forum for negotiation and formalization of a trade agreement among the member countries.
2. It settles disputes and grievances relating to trade among the member countries.
3. It frames a commonly accepted code of conduct in order to reduce trade barriers.
4. It holds consultations with IMF and World Bank (IBRD) and its affiliates to bring about a greater understanding and cooperation in global economic policymaking.
5. It supervises the operations of the agreement relating to the General Agreement on Tariffs and Trade(GATT) and Trade.
6. Related Intellectual Properties Rights (TRIPS)
7. It regulates trade between participating countries.

Question 3.
Describe the benefits of WTO.
Answer:
Meaning: The World Trade Organisation (WTO) was established on 1 st January 1995. The GATT was renamed as WTO with some changes. WTO has 164 member countries as of 29th July 2016. The ministerial conference consisting of the representatives of all the member countries is the highest decision-making authority of WTO.
Some of the major benefits of WTO are as follows.

• WTO is promoting international peace and creating a conducive environment for conducting international trade
• It settles the trade disputes amicably among the member countries.
• It promotes the standard of living of people by increasing their income level from free trades
• WTO has removed quantitative restrictions and non-tariff barriers. It has facilitated the free flow of foreign trade among the member countries.
• The countries can impose import restrictions only to correct balance of payments difficulties and not otherwise.
•  It stimulates the economic growth of developing countries by providing them with much-needed capital and giving them preferential treatment in trade-related matters.

Question 4.
Highlights the functions of IBRD.
Answer:

1. Assisting reconstruction of war-affected countries.
2. Promoting economic growth and balanced growth of the international business.
3. Promoting infrastructural facilities like energy and transportation, road development, etc. in member countries.
4. Encouraging agricultural and industrial development in developing countries by providing adequate resources.
5. Providing resources for promoting sanitation, education, health care and small scale enterprises in member countries.
6. Improving standard of living of people of member countries by providing assistance by removing poverty, raising productivity, providing technical support and conducting research and development.

Question 5.
Write down the functions of IMF.
Answer:
International Monetary fund (IMF) is an international organization headquartered in Washington DC. It has a membership of 189 countries. It was established in 27th December 1945 on the recommendation of the Bretton Wood Conference. It provides a shorter loan to member countries to their correct balance of payments disequilibrium.
Functions of IMF:
The functions of IMF are enumerated below

• It acts as short term credit institution at the international level.
• It provides machinery for ordinary adjustments of exchange rates.
• It has a reservoir of currencies of the member countries from which a borrower can borrow currencies of other nations.
• It promotes economic stability and global growth by encouraging countries to adopt sound economic and financial policies.
• It offers technical assistance and training to help member countries strengthen and implement effective policies. Technical assistance is offered in formulating banking, fiscal, monetary, and exchange policies.
• It helps member countries correct their imbalance in the balance of payment.

Question 6.
Explain how far India has benefited from IMF.
Answer:
Free Convertibility of Indian Rupee:
The Indian rupee has become independent after the establishment of IMF. Earlier it was linked with the pound sterling. Its value is now determined in terms of Gold. Hence it is freely convertible.

1. Loan For Development Activities: India got several loan facilities from IMF for its several development projects.
2. Ability To Purchase Foreign Currency: Government of India is able to purchase foreign currencies from time to time to meet the ever growing requirement of development activities.
3. Expert Advice: India used to get expert advice from IMF for solving the economic problems. It has given valuable advice to India with regard to financing its 5-year plan.
4. Timely Help: India has received timely help from IMF many a time to eliminate the deficit in its balance of payments. India got help from IMF during 1966 in the aftermath of the war with Pakistan. It received assistance from IMF for combating oil shock. Between 1980 and 1983 India got assistance from IMF to manage the global economic recession.
5. Financial Assistance during Natural Calamity: India has got a lot of financial assistance from IMF to solve the economic crises arising from natural calamities like floods, famine, earthquake, aggressions of Chinese and Pakistan etc. It gets technical assistance from IMF.
6. Membership in World Bank: By virtue of its membership in IMF India could become a member of the World Bank.
7. Help During 1991 Economic Crisis: During 1990, India faced a serious economic crisis. Indian Government was almost nearing bankruptcy. It got assistance from IMF by pledging ‘ its gold reserve with it to solve its balance of payments crisis.

For Own Thinking

Question a.
A vital role played in international business by WTO?
Answer:
The main goal of WTO is to help the trading industry to become smooth, fair, free and predictable.

Question b.
The necessity for the world as a global village through IMF, IBRD, and SAARC?
Answer:

1. IMR – International Monetary Fund
2. IBRD – International Bank of Reconstruction and Development
3. SAARC – South Asian Association for Regional Cooperation.

For Future Learning

Question a.
WTO – new agreements?
Answer:
TFA entered into force on 22 February 2017 following its ratification by two-thirds of the WTO membership.

Question b.
IMF World Bank and SAARC major role in international business?
Answer:

1. IMF – It works to foster global growth and economic stability by providing the policy.
2. World Bank – Provide long – term loans to developing countries for development.
3. SAARC – The independence of nations has been increased.