Tamil Nadu 11th Physics Model Question Paper 3 English Medium

Students can Download Tamil Nadu 11th Physics Model Question Paper 3 English Medium Pdf, Tamil Nadu 11th Physics Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

TN State Board 11th Physics Model Question Paper 3 English Medium

Instructions:

1. The question paper comprises of four parts
2. You are to attempt all the parts. An internal choice of questions is provided wherever: applicable
3. All questions of Part I, II, III, and IV are to be attempted separately
4. Question numbers 1 to 15 in Part I are Multiple choice Questions of one mark each. These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer
5. Question numbers 16 to 24 in Part II are two-mark questions. These are lo be answered in about one or two sentences.
6. Question numbers 25 to 33 in Part III are three-mark questions. These are lo be answered in about three to five short sentences.
7. Question numbers 34 to 38 in Part IV are five-mark questions. These are lo be answered in detail. Draw diagrams wherever necessary.

Time: 3 Hours
Max Marks: 70

PART – I

Answer all the questions. [15 x 1 = 15]
Question 1.
A force F is applied on a square plate of side L. If percentage error in determination of L is 2% and that in F is 4%, the permissible error in pressure is ……….. .
(a) 2%
(b) 4%
(c) 6%
(d) 8%
Answer:
(d) 8%
Hint:
Pressure P = \(\frac { F }{ A }\) = \(\frac { F }{ L² }\)
\(\frac { ∆P }{ P }\) × 100 = (\(\frac { ∆F }{ F }\) × 100) + (\(\frac { ∆L }{ L }\) × 100) = 4% + 2(2%)
\(\frac { ∆P }{ P }\) × 100 = 8%

Question 2.
From the displacement – time graph shown below, particle is ……….. .

(a) continuously going in positive x – direction
(b) at rest
(c) going with increasing velocity upto a time t₀ and then becomes constant
(d) moves at a constant velocity upto a time t₀, and then stops
Answer:
(d) moves at a constant velocity upto a time t₀, and then stops

Question 3.
The potential energy of the system increases if work is done ……….. .
(a) upon the system by a non conservative force
(b) by the system against a conservative force
(c) by the system against a non conservative force
(d) upon the system by a conservative force
Answer:
(b) by the system against a conservative force

Question 4.
If x = at² + bt + c where x is displacement as a function of time. The dimension of ‘a’ and ‘b’ are respectively ……… .
(a) LT^-1 and LT^-2
(b) LT^-2 and LT^-1
(c) L and LT^-2
(d) LT^-1 and L
Answer:
(b) LT^-2 and LT^-1
Hint:
According to principle of homogeneity, the displacement, x = at² + bt + c
Dimensionally, [L] = [LT^-2] [T²] + [LT^-1] [T]
Where a = LT^-2 and b = LT^-1

Question 5.
A satellite in its orbit around earth is weightless on account of its ……….. .
(a) momentum
(b) acceleration
(c) speed
(d) none
Answer:
(b) acceleration

Question 6.
The displacement of a particle along x – axis is given by x = 7t² + 8t + 3. Its acceleration and velocity at t = 2s respectively ……….. .
(a) 36 ms^-1, 14 ms^-2
(b) 14 ms^-2, 36 ms^-1
(c) 47 ms^-2, 21 ms^-1
(d) 2 ms^-1, 47 ms^-2
Answer:
(b) 14 ms^-2, 36 ms^-1
Hint:
x = 7t² + 8t + 3 dx
V = \(\frac { dx }{ dt }\) = 14t + 8;
at t = 2s; V = 36 ms^-1
a = \(\frac { dv }{ dt }\) = 14 ms^-2

Question 7.
A sphere of radius r cm falls from rest in a viscous liquid. Heat is produced due to viscous force. The rate of production of heat when the sphere attains its terminal velocity is proportional to ……….. .
(a) r²
(b) r³
(c) r⁴
(d) r⁵
Answer:
(d) r⁵
Hint:
Rate of heat production = F.V
= 6πηrv × v = 6πηrv²
[v ∝ r²] Terminal velocity ∝ r⁵

Question 8.
A body of weight mg is hanging on a string which extends its length l. The workdone in extending the string is ……….. .
(a) mgl
(b) \(\frac { mgl }{ 2 }\)
(c) 2 mgl
(d) none of these
Answer:
(b) \(\frac { mgl }{ 2 }\)
Hint:
The extension length is
Workdone (W) = Force × distance
Workdone in extension string = Weight × Length extension
mg × \(\frac { l }{ 2 }\)
W = \(\frac { mgl }{ 2 }\)

Question 9.
If S_p and S_v denote the specific heat of nitrogen gas per unit mass at constant pressure and constant volume respectively, then ……….. .
(a) S_p– S_v = 28R
(b) S_p – S_v = \(\frac { R }{ 28 }\)
(c) S_p – S_v = \(\frac { R }{ 14 }\)
(d) S_p – S_v = R
Answer:
(b) S_p – S_v = \(\frac { R }{ 28 }\)
Hint:
According to Mayer’s relation, S_p – S_v = \(\frac { R }{ m }\)
For Nitrogen, m = 28
S_p – S_v = \(\frac { R }{ 28 }\)

Question 10.
A particle is moving eastwards with velocity of 5 m/s. In 10 sec the velocity changes to 5 m/s northwards. The average acceleration in this time is ……….. .
(a) zero
(b) \(\frac { 1 }{ √2 }\) m/s² towards north – west
(c) \(\frac { 1 }{ √2 }\) m/s² towards north – east
(d) \(\frac { 1 }{ 2 }\) m/s² towards north – west
Answer:
(b) \(\frac { 1 }{ √2 }\) m/s² towards north – west
Hint:

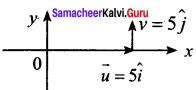
\(\vec { a } \) = \(\frac { d\vec { v } }{ dt }\)
= \(\frac { 5 }{ 2 } (\hat { j } -\hat { i) } \)
= \(\frac { 1 }{ 2 } (\hat { j } -\hat { i) } \)
a = \(\frac { 1 }{ √2 }\) m/s^-2

Question 11.
In an isochoric process, we have ……….. .
(a) W ≠ 0, U = 0, Q = 0, T = 0
(b) W ≠ 0, U ≠ 0, Q = 0, T = 0
(c) W = 0, U = 0, Q ≠ 0, T ≠ 0
(d) W = 0, U ≠ 0, Q ≠ 0, T ≠ 0
Answer:
(d) W = 0, U ≠ 0, Q ≠ 0, T ≠ 0

Question 12.
The efficiency of a carnot engine operations between boiling and freezing points of water is ……….. .
(a) 0.1
(b) 100
(c) 1
(d) 0.27
Answer:
(d) 0.27
Hint:
η = [1 – (\(\frac { { T }_{ 2 } }{ { T }_{ 1 } } \))] = [1 – \(\frac { 273 }{ 373 }\)]
η = 0.268
∴ η = 0.27

Question 13.
Bernoulli’s equation is consequences of conservation of ……….. .
(a) energy
(b) linear momentum
(c) angular momentum
(d) mass
Answer:
(a) energy

Question 14.
By what velocity a ball be projected vertically upwards so that the distance covered in 5th second is twice of that covered in 6 m second (tale g = 10 ms^-2) ……….. .
(a) 19.6 ms^-1
(b) 58.8 ms^-1
(c) 49 ms^-1
(d) 65 ms^-1
Answer:
(d) 65 ms^-1
Hint:
Distance covered int he 5^th second
S₅= u + \(\frac { 1 }{ 2 }\)(-10) × (2 × 5 – 1)
S₅ = u – 5 × 9 = u – 45
Distance covered in the 6^th second
S₆= u +\(\frac { 1 }{ 2 }\)(-10) × (2 × 6 – 1) = u – 5 × 11
S₆ = u – 55 .
Here S₅ = 6S₆ and we get solving
u = 65 ms^-1

Question 15.
Unit of Stefan’s constant is ……….. .
(a) watt m² k⁴
(b) watt m² / k⁴
(c) watt k⁴ / m²
(d) watt / m² k⁴
Answer:
(d) watt / m² k⁴

PART – II

Answer any six questions in which Q. No 23 is compulsory. [6 × 2 = 12]

Question 16.
Get an expression for stopping distance of a vehicle in terms of initial velocity v₀ and deceleration ‘a’.
Answer:
Let s be the distance travelled by a vehicle before it stops
Using v² – u² = 2as,
We can get 0² – \(v_{0}^{2}\) = -2as
∴ s = \(\frac{v_{0}^{2}}{2a}\)
The stopping distance is directly proportional to \(v_{0}^{2}\). i.e. By doubling initial velocity it increase stopping distance by 4 times. Provided deceleration is kept as constant.

Question 17.
A carnot engine has the same efficiency, when operated
(i) between 100 K and 500 K
(ii) between TK and 900 K. Find the value of T.
Answer:
(i) Here T₁ = 500 K; T₂ = 100 K
η = 1 – \(\frac{T_2}{T_1}\) =1 – \(\frac{100}{500}\) = 1 – 0.2 = 0.8

(ii) Now, T₁= 900 K; T₂ = T and n = 0.8
Again, η = 1 – \(\frac{T_2}{T_1}\)
0.8 = 1 – \(\frac{T}{900}\) = 1 – 0.8 = 0.2
∴ T = 180K

Question 18.
A block at rest explodes into 3 parts are -2p\(\vec{j}\) and p\(\vec{j}\). Calculate the magnitude of the momentum of the third part.
Answer:
Let \(\vec{P}\) be the momentum of third particle after the explosion of bomb. According to law of conservation of momentum
-2p\(\vec{i}\) + p\(\vec{j}\) + \(\vec{P}\) = 0 (or) \(\vec{P}\) = 2p\(\vec{i}\) – p\(\vec{j}\)
P = \(\sqrt{(2p)^2+(-p)^2}\) = p√5

Question 19.
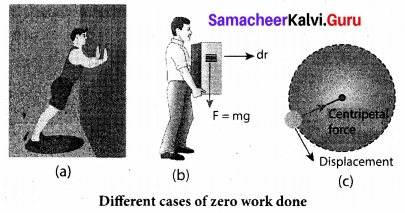
Discuss the possibilities of work done to be zero.
Answer:
Work done is zero in the following cases.
(i) When the force is zero (F = 0). For example, a body moving on a horizontal smooth frictionless surface will continue to do so as no force (not even friction) is acting along the plane. (This is an ideal situation.)

(ii) When the displacement is zero (dr = 0). For example, when force is applied on a rigid wall it does not produce any displacement. Hence, the work done is zero as shown in figure.

(iii) When the force and displacement are perpendicular (θ = 90°) to each other, when a body moves on a horizontal direction, the gravitational force (mg) does not work on the body, since it acts at right angles to the displacement as shown in Figure (b). In circular motion the centripetal force does not do work on the object moving on a circle as it is always perpendicular to the displacement as shown in Figure (c).

Question 20.
Define (a) unit of length (b) unit of electric current in SI system.
Answer:
Given v = at² + \(\frac{b}{c+t}\)
The physical quantities which are having same dimensional formula only can be added.
Dimensional formula for v = LT^-1
Dimensional formula for c = T
Dimensional formula for at² = LT^-1
a = \(\frac{LT_{-1}}{T^2}\) = LT^-3
Dimensional formula for \(\frac{b}{c+t}\) = LT^-1
∴ b = L [∵ c + t = T]

Question 21.
A solid cylinder of mass 20 kg rotates about it axis with angular speed 100 s^-1 the radius of the cylinder is 0.25 m. Calculate moment of inertia of the solid cylinder.
Answer:
Given Data : R = 0.25 m, M = 20 kg, ω = 100 s^-1
We know that
moment of inertia of the solid cylinder = \(\frac{MR^2}{2}\)
\(\frac{20×(0.25)^2}{2}\) = 0.625 kgm²
K.E of rotation = \(\frac{1}{2}\) Iω²
\(\frac{1}{2}\) × 0.625 × (100)² = 3125 J
∴ Angular momentum L = Iω = 0.625 × 100
L = 62.5 Js

Question 22.
Why moon has no atmosphere?
Answer:
The acceleration due to gravity of moon ‘g’ is small. Therefore the escape velocity on the surface of moon is also small. The molecules of in its atmosphere have greater thermal velocities than escape speed. The molecules can easily escaped from the atmosphere of moon. Hence the moon has no atmosphere.

Question 23.
A refrigerator has cop of 3. How much work must be supplied to the refrigerator in order to remove 200 J of heat from its interion?
Answer:
COP = β = \(\frac{Q_L}{W}\)
W = \(\frac{Q_c}{COP}\) = \(\frac{200}{3}\) = 66.67 J

Question 24.
What is the effect of gravitational force of attraction acting on the person be inside the satellite and stand on moon?
Answer:
The gravitational force of attraction of the Earth on the person inside the satellite provides the centripetal force necessary to move in an orbit. A person standing on the moon possesses weight due to the additional gravitational pull of the moon on the person.

PART – III

Answer any six questions in which Q.No. 29 is compulsory. [6 × 3 = 18]

Question 25.
State and prove Archimedes principle.
Answer:
Archimedes Principle: It states that when a body is partially or wholly immersed in a fluid, it experiences an upward thrust equal to the weight of the fluid displaced by it and its upthrust acts through the centre of gravity of the liquid displaced.

Proof: Consider a body of height ‘h’ lying inside a liquid of density p, at a depth x below the free surface of the liquid. Area of cross section of the body is V. The forces on the sides of the body cancel out.

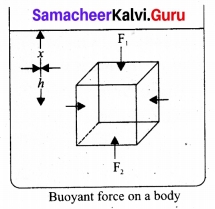
Pressure at the upper face of the body, P_1′ = xpg.
Pressure at the lower face of the body, P_2′ = (x + h) pg
Thrust acting on the upper face of the body is F₁ = P₁ a = xρga acting vertically downwards,
Thrust acting on the lower face of the body is F₂ = P₂a = (x + h) ρga acting vertically upwards.
The resultant force (F₂ – F₁) is acting on the body in the upward direction and is called upthrust (U).
U = F₂ – F₁ = (x + h) ρga – xρga = ahρg
But ah = V, Volume of the body = Volume of liquid
U = Vρg = Mg
i. e., Upthrust or buoyant force = Weight of liquid displaced.
This proves the Archimedes principle.

Question 26.
State kepler’s three laws.
Answer:

1. Law of Orbits: Each planet moves around the Sun in an elliptical orbit with the Sun at one of the foci.
2. Law of area: The radial vector (line joining the Sun to a planet) sweeps equal areas in equal intervals of time.
3. Law of period: The square of the time period of revolution of a planet around the Sun in its elliptical orbit is directly proportional to the cube of the semi-major axis of the ellipse.
   T² ∝ a³
   \(\frac{T²}{a³}\) = Constant

Question 27.
Write the properties of vector product of two vectors.
Answer:
Properties of vector product of two vectors are:
(i) The vector product of any two vectors is always another vector whose direction is perpendicular to the plane containing these two vectors, i.e., orthogonal to both the vectors \(\vec{A}\) and \(\vec{B}\), even though the vectors \(\vec{A}\) and \(\vec{B}\) may or may not be mutually orthogonal.

(ii) The vector product of two vectors is not commutative, i.e., \(\vec{A}\) × \(\vec{B}\) ≠ \(\vec{B}\) × \(\vec{A}\). But, \(\vec{A}\) × \(\vec{B}\) = –\(\vec{B}\) × \(\vec{A}\).

Here it is worthwhile to note that |\(\vec{A}\) × \(\vec{B}\)| = |\(\vec{B}\) x \(\vec{A}\)| = AB sin θ i.e., in the case of the product vectors \(\vec{A}\) × \(\vec{A}\) and \(\vec{B}\) × \(\vec{A}\), the magnitudes are equal but directions are opposite to each other.

(iii) The vector product of two vectors will have maximum magnitude when sin θ = 1, i.e., θ = 90° i.e., when the vectors \(\vec{A}\) and \(\vec{B}\) are orthogonal to each other.
(\(\vec{A}\) × \(\vec{B}\))_max = AB\(\hat{n}\)

(iv) The vector product of two non-zero vectors will be minimum when sin θ = 0, i.e., θ = 0° or 180°
(\(\vec{A}\) × \(\vec{B}\))_min = 0
i.e., the vector product of two non-zero vectors vanishes, if the vectors are either parallel or antiparallel.

(v) The self-cross product, i.e., product of a vector with itself is the null vector
\(\vec{A}\) × \(\vec{A}\) = AA sin 0° \(\hat{n}\) = \(\vec{0}\)
In physics the null vector \(\vec{0}\) is simply denoted as zero.

(vi) The self-vector products of unit vectors are thus zero.
\(\vec{i}\) × \(\vec{i}\) = \(\vec{j}\) × \(\vec{j}\) = \(\vec{k}\) × \(\vec{k}\) = 0

Question 28.
Let the two springs A and B such that K_A > K_B on which spring will more work has to be done if they are stretched by the same force.
Answer:
F = K.x so x = \(\frac{F}{K}\)
For same F

Question 29.
Differentiate slipping and sliding.
Answer:

	Sliding	Slipping
(i)	Velocity of centre of mass is greater than Rω i.e. VCM > Rω.	Velocity of centre of mass is lesser than Rω. i.e. VCM < Rω
(ii)	Velocity of translational motion is greater than velocity of rotational motion.	Velocity of translation motion is lesser than velocity of rotational motion.
(iii)	Resultant velocity acts in the forward direction.	Resultant velocity acts in the backward direction.

Question 30.
Jupiter is at a distance of 824.7 million km from the earth. Its angular diameter is measured to be 35.72” calculate the diameter of Jupiter.
Answer:
Distance of Jupiter = 824.7 × 10⁶ km = 8.247 × 10¹¹ m
Angular diameter = 35.72 × 4.85 × 10^-6 rad = 173.242 × 10^-6 rad
= 1.73 × 10^-4 rad
Diameter of Jupiter D = θ × d= 1.73 × 10^-4 rad × 8.247 × 10¹¹ m
= 14.267 × 10⁷m = 1.427 × 10⁸m (or) 1.427 × 10⁵ km

Question 31.
A wire 10 m long has a cross-sectional area 1.25 × 10^-4 m². It is subjected to a load of 5 kg. If young’s modulus of the material is 4 × 10¹⁰ Nm^-2. calculate the elongation produced in the wire, [take g = 10 ms^-2]
Answer:
We know that

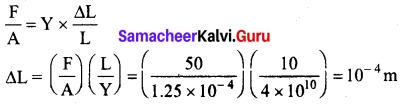
Question 32.
State and explain the law of equipartition of energy.
Answer:
According to kinetic theory, the average kinetic energy of system of molecules in thermal equilibrium at temperature T is uniformly distributed to all degrees of freedom (x or y or z directions of motion) so that each degree of freedom will get \(\frac{1}{2}\) kT of energy. This is called law of equipartition of energy.
Average kinetic energy of a monatomic molecule (with f = 3) = 3 × \(\frac{1}{2}\) KT = \(\frac{3}{2}\) KT
Average kinetic energy of diatomic molecule at low temperature (with f = 5) = 5 × \(\frac{1}{2}\) KT = \(\frac{5}{2}\) KT
Average kinetic energy of a diatomic molecule at high temperature (with f = 7) = 7 × \(\frac{1}{2}\) KT = \(\frac{7}{2}\) KT
Average kinetic energy of linear triatomic molecule (with f = 7) = 7 × \(\frac{1}{2}\) KT = \(\frac{7}{2}\) KT
Average kinetic energy of non linear triatomic molecule (with f = 6) = 6 × \(\frac{1}{2}\) KT = 3 KT

Question 33.
A cylindrical tank of height 0.4 m is open at the top and has a diameter 0.16 m. Water is filled in it up to height of 0.16 m. Find the time taken to empty the tank through a hole of radius 5 × 10^-3 m in its bottom.
Answer:
The velocity of efflux through the hole v = \(\sqrt{2gh}\)
Let R, r be the radius of cylindrical tank and hole and ‘dh’ is the decrease in height of water in time ‘dt’ sec use principle of continuity at the top and hole

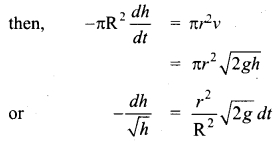
integrating it within the condition of problem,

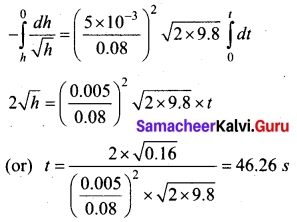
PART – IV

Answer all the questions. [5 × 5 = 25]

Question 34 (a).
Show that the path of oblique projection is parabola.
Answer:
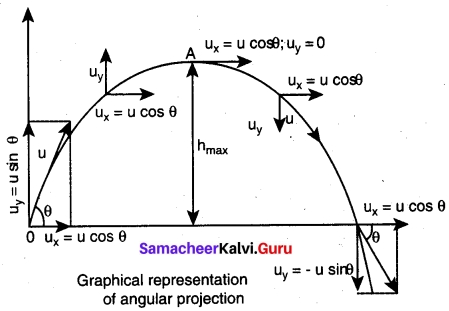
This projectile motion takes place when the initial velocity is not horizontal, but at some angle with the vertical, as shown in Figure.(Oblique projectile)
Examples:

1. Water ejected out of a hose pipe held obliquely.
2. Cannon fired in a battle ground.

Consider an object thrown with initial velocity at an angle θ with the horizontal.
Then,
u = u\(\vec{i}\) + u\(\vec{j}\)
where u = u cos θ is the horizontal component and u = u sin θ, the vertical component of velocity.

Since the acceleration due to gravity is in the direction opposite to the direction of vertical component u_y, this component will gradually reduce to zero at the maximum height of the projectile. At this maximum height, the same gravitational force will push the projectile to move downward and fall to the ground. There is no acceleration along the x direction throughout the motion. So, the horizontal component of the velocity (u_x = u cos θ) remains the same till the object reaches the ground.

Hence after the time t, the velocity along horizontal motion v_x = u_x + a_xt = u_x = u cos θ
The horizontal distance travelled by projectile in time t is s_x = u_xt + \(\frac{1}{2}\) a_xt²
Here, s_x = x, u_x = u cos θ, a_x = 0

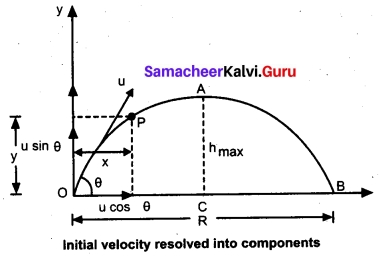
Thus, x = u cos θ.t or t = \(\frac{x}{u cos θ }\) ………..(1)
Next, for the vertical motion v_y = u_y + a_yt
Here u_y = u sin θ, a_y = -g (acceleration due to gravity acts opposite to the motion).
Thus, v_y = u sin θ – gt
The vertical distance travelled by the projectile in the same time t is
Here, s_y = y, u_y = u sin θ, a_x = -g
Then y = u sin θ t – \(\frac{1}{2}\) gt² ……..(2)
Substitute the value of t from equation (1) in equation (2), we have

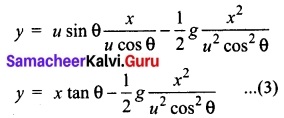
Thus the path followed by the projectile is an inverted parabola.

[OR]

(b) Explain the motion of block connected by a string in vertical motion.
Answer:

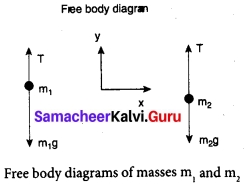
Case 1: Vertical motion: Consider two blocks of masses m₁ and m₂ (m₁ > m₂) connected by a light and inextensible string that passes over a pulley as shown in figure.

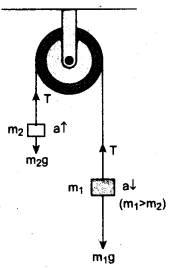
Let the tension in the string be T and acceleration a. When the system is released, both the blocks start moving, m₂ vertically upward and m₁ downward with same acceleration a. The gravitational force m₁g on mass m₁ is used in lifting the mass m₂.
The upward direction is chosen as y direction. The free body diagrams of both masses are shown in figure.
Applying Newton’s second law for mass m₂
T\(\hat{j}\) – m₂g\(\hat{j}\) = m₂a\(\hat{j}\)
The left hand side of the above equation is the total force that acts on m₂ and the right hand side is the product of mass and acceleration of m₂ in y direction.
By comparing the components on both sides, we get
T – m₂g = m₂a …..(1)
Similarly, applying Newton’s second law for mass m₁
T\(\hat{j}\) – m₁g\(\hat{j}\) = -m₁a\(\hat{j}\)
As mass m₁ moves downward (-\(\hat{j}\)), its acceleration is along (-\(\hat{j}\))
By comparing the components on both sides, we get
T – m₁g = -m₁a
m₁g – T = m₁a ……(2)
Adding equations (1) and (2), we get
m₁g – m₂g = m₁a – m₂a
(m₁ – m₂)g = (m₁ + m₁)a ……(3)
From equation (3), the acceleration of both the masses is
a = (\(\frac{m_1-m_2}{m_1+m_2}\))g …….(4)
If both the masses are equal (m₁ = m₂), from equation (4)
a = 0
This shows that if the masses are equal, there is no acceleration and the system as a whole will be at rest.
To find the tension acting on the string, substitute the acceleration from the equation (4) into the equation (1).

Equation (4) gives only magnitude of acceleration.
For mass m₁, the acceleration vector is given by \(\vec{a}\) = –\(\frac{m_1-m_2}{m_1+m_2}\)g\(\hat{j}\)
For mass m₂, the acceleration vector is given by \(\vec{a}\) = \(\frac{m_1-m_2}{m_1+m_2}\)g\(\hat{j}\)

Question 35 (a).
Derive the expression for Carnot engine efficiency.
Answer:
Efficiency of a Carnot engine: Efficiency is defined as the ratio of work done by the working substance in one cycle to the amount of heat extracted from the source.
η = \(\frac{Workdone}{Heat extracted}\) = \(\frac{W}{Q_H}\) ……..(1)
From the first law of thermodynamics, W = Q_H – Q_L
η = \(\frac{Q_H – Q_L}{Q_H}\) = 1 – \(\frac{Q_L}{Q_H}\) ……..(2)
Applying isothermal conditions, we get,
Q_H = μRT_Hln \(\frac{V_2}{V_1}\)
Q_L = μRT_Lln \(\frac{V_3}{V_4}\) ………(3)
Here we omit the negative sign. Since we are interested in only the amount of heat (Q_L) ejected into the sink, we have
\(\frac{T_L}{T_H}\) = \(\frac{Q _L ln (\frac{V_3}{V_4})}{Q _H ln (\frac{V_2}{V_1})}\) …….(4)
By applying adiabatic conditions, we get,
\(\mathrm{T}_{\mathrm{H}} \mathrm{V}_{2}^{\gamma-1}=\mathrm{T}_{\mathrm{L}} \mathrm{V}_{3}^{\gamma-1}\)
\(\mathrm{T}_{\mathrm{H}} \mathrm{V}_{1}^{\gamma-1}=\mathrm{T}_{\mathrm{L}} \mathrm{V}_{4}^{\gamma-1}\)
By dividing the above two equations, we get
\(\left(\frac{v_{2}}{V_{1}}\right)^{\gamma-1}=\left(\frac{V_{3}}{V_{4}}\right)^{\gamma-1}\)
Which implies that \(\frac{V_2}{V_1}\) = \(\frac{V_3}{V_4}\) ……(5)
Substituting equation (5) in (4), we get
\(\frac{Q_L}{Q_H}\) = \(\frac{T_L}{T_H}\) ……..(6)
∴ The efficiency η = 1 – \(\frac{T_L}{T_H}\) ………….(7)
Note : T_L and T_H should be expressed in Kelvin scale.

Important results:

1. n is always less than 1 because T_L is less than T_H. This implies the efficiency cannot be 100%.
2. The efficiency of the Carnot’s engine is independent of the working substance. It depends only on the temperatures of the source and the sink. The greater the difference between the two temperatures, higher the efficiency.
3. When T_H = T_L the efficiency n = 0. No engine can work having source and sink at the same temperature.

[OR]

(b). Explain the concepts of fundamental frequency, harmonics and overtones in detail.
Answer:
Fundamental frequency and overtones: Let us now keep the rigid boundaries at x = 0 and x = L and produce a standing waves by wiggling the string (as in plucking strings in a guitar). Standing waves with a specific wavelength are produced. Since, the amplitude must vanish at the boundaries, therefore, the displacement at the boundary must satisfy the following conditions y(x = 0, t) = 0 and y(x = L, t) = 0………….(1)
Since, the nodes formed are at a distance \(\frac{ λ_n}{2}\) apart, we have n \(\frac{ λ_n}{2}\) = L where n is an integer, L is the length between the two boundaries and λ _n is the specific wavelength that satisfy the specified boundary conditions. Hence,
λ _n = \(\frac{2L}{n}\)…………(2)
Therefore, not all wavelengths are allowed. The (allowed) wavelengths should fit with the specified boundary conditions, i.e., for n = 1, the first mode of vibration has specific wavelength λ _n= 2L. Similarly for n = 2, the second mode of vibration has specific wavelength
λ ₂ = \(\frac{2L}{2}\) = L
For n = 3, the third mode of vibration has specific wavelength
λ ₃ = \(\frac{2L}{3}\)
and so on.
The frequency of each mode of vibration (called natural frequency) can be calculated.
We have, f_n = \(\frac{v}{λ_n}\) = n \(\frac{v}{2L}\) ………..(3)
The lowest natural frequency is called the fundamental frequency.
f₁ = \(\frac{v}{λ_1}\) = \(\frac{v}{2L}\) …………(4)
The second natural frequency is called the first over tone.
f₂ = 2\(\frac{v}{2L}\) = \(\frac{1}{L} \sqrt{\frac{T}{\mu}}\)
The third natural frequency is called the second over tone.
f₃ = 3\(\frac{v}{λ_2}\) = \(3\left(\frac{1}{2L} \sqrt{\frac{T}{\mu}}\right)\)
and so on.
Therefore, the nth natural frequency can be computed as integral (or integer) multiple of fundamental frequency, i.e.,
f_n = nf₁, where n is an integer …….(5)
If natural frequencies are written as integral multiple of fundamental frequencies, then the frequencies are called harmonics. Thus, the first harmonic is f₁ = f₁(the fundamental frequency is called first harmonic), the second harmonic is f₂ = 2f₁, the third harmonic is f₃ = 3f₁ etc.

Question 36 (a).
Compare any two salient features of static and kinetic friction.
Answer:
Static Friction: Static friction is the force which opposes the initiation of motion of an object on the surface. The magnitude of static frictional force f_s lies between 0 ≤ f_s ≤ μ_sN_s
where,
_μs – coefficient of static friction
N – Normal force
Kinetic friction: The frictional force exerted by the surface when an object slides is called as kinetic friction. Also called as sliding friction or dynamic friction,
f_k = μ_kN
where:
μ_k– the coefficient of kinetic friction
N – Normal force exerted by the surface on the object

(ii) To move an object-push or pull? Which is easier? Explain.
Answer:
When a body is pushed at an arbitrary angle θ (0 to \(\frac{π}{2}\)), the applied force F can be
resolved into two components as F sin θ parallel to the surface and F cos θ perpendicular to the surface as shown in figure. The total downward force acting on the body is mg + F cos θ. It implies that the normal force acting on the body increases. Since there is no acceleration along the vertical direction the normal force N is equal to
N_Push = mg + F cos θ ….(1)
As a result the maximal static friction also increases and is equal to
\(f_{x}^{\max }\) = μ_rN_Push = μ_s(mg + F cos θ ) ……(2)
Equation (2) shows that a greater force needs to be applied to push the object into motion.

When an object is pulled at an angle θ, the applied force is resolved into two components as shown in figure. The total downward force acting on the object is
N_Pull = mg – F cos θ ……..(3)

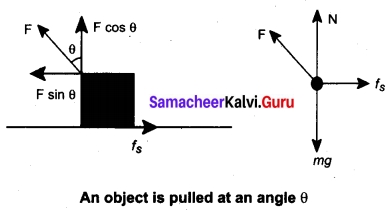
Equation (3)shows that the normal force is less than N_Pull. From equations (1) and (3), it is easier to pull an object than to push to make it move.

[OR]

(b). Describe the vertical oscillations of a spring.
Answer:
Vertical oscillations of a spring: Let us consider a massless spring with stiff ness constant or force constant k attached to a ceiling as shown in figure. Let the length of the spring before loading mass m be L. If the block of mass m is attached to the other end of spring, then the spring elongates by a length l. Let F₁, be the restoring force due to stretching of spring. Due to mass m, the gravitational force acts vertically downward. We can draw free-body diagram for this system as shown in figure. When the system is under equilibrium,
F₁+ mg = 0 ……(1)
But the spring elongates by small displacement 1, therefore,
F₁ ∝ l ⇒ F₁ = -kl …(2)
Substituting equation (2) in equation (1), we get – kl + mg = 0
-kl + mg = 0
mg = l or \(\frac{m}{k}\) = \(\frac{l}{g}\) …….(3)

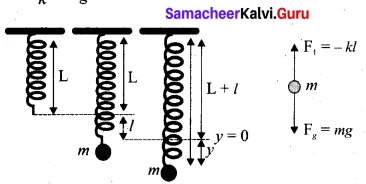
Suppose we apply a very small external force on the mass such that the mass further displaces downward by a displacement y, then it will oscillate up and down. Now, the restoring force due to this stretching of spring (total extension of spring is( y + 1) is
F2 ∝ (y + l)
F2 = -k(y + l) = -ky – kl …..(4)
Since, the mass moves up and down with acceleration \(\frac{d^2y}{dt^2}\) diagram for this case, we get
-ky – kl + mg = m\(\frac{d^2y}{dt^2}\) …….(5)
The net force acting on the mass due to this stretching is
F = F₂ + mg
F = – ky – kl + mg ……..(6)
The gravitational force opposes the restoring force. Substituting equation (3) in equation (6), we get
F = – ky – kl + kl = -ky
Applying Newton’s law, we get
m\(\frac{d^2y}{dt^2}\) = -ky
m\(\frac{d^2y}{dt^2}\) = –\(\frac{k}{m}\)y ……(7)
The above equation is in the form of simple harmonic differential equation. Therefore, we get the time period as
T = 2π, \(\sqrt{\frac{m}{k}}\) second …….(8)
The time period can be rewritten using equation (3)
T = 2π, \(\sqrt{\frac{m}{k}}\) = 2πl\(\frac{l}{g}\) second ……(9)
The acceleration due to gravity g can be computed from the formula
g = 4π²(\(\frac{1}{T^2}\)) ms^-2

Question 37 (a).
State and prove Bernoulli’s theorem
Answer:
Bernoulli’s theorem: According to Bernoulli’s theorem, the sum of pressure energy, kinetic energy, and potential energy per unit mass of an incompressible, non-viscous fluid in a streamlined flow remains a constant. Mathematically,
\(\frac{p}{roe}\) + \(\frac{1}{2}\)v² + gh = Constant
This is known as Bernoulli’s equation.
Proof : Let us consider a flow of liquid through a pipe AB. Let V be the volume of the liquid when it enters A in a time t which is equal to the volume of the liquid leaving B in the same time. Let a_A, v_A and P_A be the area of cross section of the tube, velocity of the liquid and pressure exerted by the liquid at A respectively.
Let the force exerted by the liquid at A is
F_A = P_A a_A
Distance travelled by the liquid in time t is d = v_At
Therefore, the work done is W = F_Ad = P_Aa_Av_At
But a_Av_At = a_Ad = V, volume of the liquid entering at A.
Thus, the work done is the pressure energy (at A), W = F_Ad = P_AV
Pressure energy per unit volume at
A = \(\frac{pressure energy}{volume}\) = \(\frac{P_AV}{V}\) = P_A
Pressure energy per unit mass at
A = \(\frac{pressure energy}{volume}\) = \(\frac{P_AV}{m}\) = \(\frac{P_A}{\frac{m}{v}}\) = \(\frac{P_A}{ρ}\)
Since m is the mass of the liquid entering at A in a given time, therefore, pressure energy of the liquid at A is
EP_A – P_AV = P_AV × (\(\frac{m}{m}\)) = m\(\frac{P_A}{ρ}\)
Potential energy of the liquid at A,
PE_A = mgh_A
Due to the flow of liquid, the kinetic energy of the liquid at A,
KE_A = \(\frac{π}{2}\)m \(v_{A}^{2}\)
Therefore, the total energy due to the flow of liquid at A,
E_A = EP_A + KE_A + PE_A
E_A = m\(\frac{P_A}{ρ}\) + \(\frac{1}{2}\) mv\(v_{A}^{2}\) + mg h_A
Similarly, let a_B, v_B and P_B be the area of cross section of the tube, velocity of the liquid and pressure exerted by the liquid at B. Calculating the total energy at F_B, we get
E_B = m\(\frac{P_B}{ρ}\) + \(\frac{1}{2}\) mv\(v_{B}^{2}\) + mg h_B
From the law of conservation of energy,
E_A = E_B

Thus, the above equation can be written as
\(\frac{P}{ρg}\) + \(\frac{1}{2}\) \(\frac{V_2}{g}\) + h = Constant

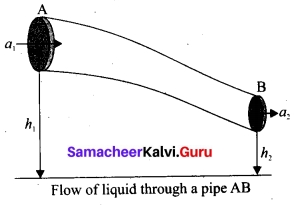
The above equation is the consequence of the conservation of energy which is true until there is no loss of energy due to friction. But iri practice, some energy is lost due to friction. This arises due to the fact that in a fluid flow, the layers flowing with different velocities exert frictional forces on each other. This loss of energy is generally converted into heat energy. Therefore, Bernoulli’s relation is strictly valid for fluids with zero viscosity or non-viscous liquids. Notice that when the liquid flows through a horizontal pipe, then
h = 0 ⇒ \(\frac{P}{ρg}\) +\(\frac{1}{2}\) \(\frac{V_2}{g}\) = Constant

[OR]

(b) Write down the postulates of kinetic theory of gases.
Answer:

1. All the molecules of a gas are identical, elastic spheres.
2. The molecules of different gases are different.
3. The number of molecules in a gas is very large and the average separation between them is larger than size of the gas molecules.
4. The molecules of a gas are in a state of continuous random motion.
5. The molecules collide with one another and also with the walls of the container.
6. These collisions are perfectly elastic so that there is no loss of kinetic energy during collisions.
7. Between two successive collisions, a molecule moves with uniform velocity.
8. The molecules do not exert any force of attraction or repulsion on each other except during collision. The molecules do not possess any potential energy and the energy is wholly kinetic.
9. The collisions are instantaneous. The time spent by a molecule in each collision is very small compared to the time elapsed between two consecutive collisions.
10. These molecules obey Newton’s laws of motion even though they move randomly.

Question 38 (a).
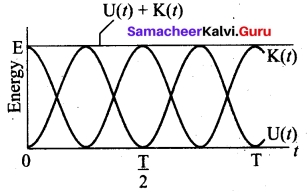
Discuss in detail the energy in simple harmonic motion.
Energy in simple harmonic motion:
Answer:
(a) Expression for Potential Energy
For the simple harmonic motion, the force and the displacement are related by Hooke’s law
\(\vec{F}\) = -k\(\vec{r}\)
Since force is a vector quantity, in three dimensions it has three components. Further, the force in the above equation is a conservative force field; such a force can be derived from a scalar function which has only one component. In one dimensional case
F = -kx ……(1)
We know that the work done by the conservative force field is independent of path. The potential energy U can be calculated from the following expression.
F = –\(\frac{dU}{dx}\)
Comparing (1) and (2), we get
–\(\frac{dU}{dx}\) = -kx
dU = kx dx
This work done by the force F during a small displacement dx stores as potential energy

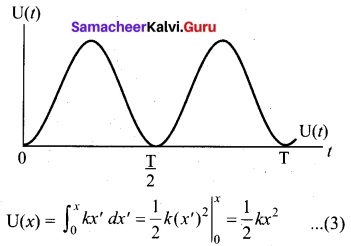
From equation to ω = \(\sqrt{\frac{k}{m}}\), we can substitute the value of force constant k = mω² in equation (3),
U(x) = \(\frac{1}{2}\)mω²x² …..(4)
where ω is the natural frequency of the oscillating system. For the particle executing simple harmonic motion from equation y = A sin ωt, we get
x = A sin ωt
U(t) = \(\frac{1}{2}\)mω²A² sin² ωt ……(5)
This variation of U is shown in figure.

(b) Expression for Kinetic Energy
Kinetic energy
KE = \(\frac{1}{2}\)m\(v_{x}^{2}\) = \(\frac{1}{2}\)m(\(\frac{dx}{dt}\))² …..(6)
Since the particle is executing simple harmonic motion, from equation
y = A sin ωt
x = A sin ωt

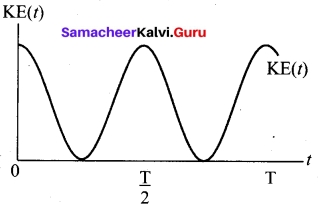
Therefore, velocity is
v_x = \(\frac{dx}{dt}\) = Aω cos ωt ….(7)

This variation with time is shown in figure.

(c) Expression for Total Energy
Total energy is the sum of kinetic energy and potential energy
E = KE + U ….(11)
E = \(\frac{1}{2}\) mω² (A² – x²) + \(\frac{1}{2}\) mω²x²
Hence, cancelling x² term,
E = \(\frac{1}{2}\) mω²A² = constant ……(12)
Alternatively, from equation (5) and equation (10), we get the total energy as
E = \(\frac{1}{2}\) mω²A² sin² ωt + \(\frac{1}{2}\) mω²A² cos² ωt
= \(\frac{1}{2}\) mω²A² (sin² ωt + cos² ωt)

From trigonometry identity, (sin² ωt + cos² ωt) = 1
E = \(\frac{1}{2}\) mω²A² = constant
which gives the law of conservation of total energy.
Thus the amplitude of simple harmonic oscillator, can be expressed in terms of total energy.
A = \(\sqrt{\frac{2E}{mω^2}}\) =\(\sqrt{\frac{2E}{k}}\)

[OR]

(b) Explain the formation of stationary waves.
Answer:
Consider two harmonic progressive waves (formed by strings) that have the same amplitude and same velocity but move in opposite directions. Then the displacement of the first wave (incident wave) is
y₁ = A sin (kx – ωt) (waves move toward right) ……(1)
and the displacement of the second wave (reflected wave) is
y₂ = A sin (kx + ωt) (waves move toward left) …….(2)
both will interfere with each other by the principle of superposition, the net displacement is
y = y₁ + y₂ ……(3)
Substituting equation (1) and equation (2) in equation (3), we get
y = A sin (kx – ωt)+A sin (kx + ωt) …….(4)
Using trigonometric identity, we rewrite equation (4) as
y(x, t) = 2A cos (ωt) sin (kx) ……(5)
This represents a stationary wave or standing wave, which means that this wave does not move either forward or backward, whereas progressive or travelling waves will move forward or backward. Further, the displacement of the particle in equation (5) can be written in more compact form,
y(x, t) = A’ cos (ωt)
where, A’ = 2A sin (kx), implying that the particular element of the string executes simple harmonic motion with amplitude equals to A’. The maximum of this amplitude occurs at positions for which
sin (kx) = 1 ⇒ kx = \(\frac{π}{2}\), \(\frac{3π}{2}\), \(\frac{5π}{2}\), …… = mπ
where m takes half integer or half integral values. The position of maximum amplitude is known as antinode. Expressing wave number in terms of wavelength, we can represent the anti-nodal positions as
x_m = (\(\frac{2m+1}{2}\)) \(\frac{λ}{2}\) where> m = 0, 1, 2…. ……(6)
For m = 0we have maximum at x₀ = \(\frac{λ}{2}\)
For m = 1 we have maximum at x₁ = \(\frac{3λ}{4}\)
For m = 2 we have maximum at x₂ = \(\frac{5λ}{4}\) and so on.
The distance between two successive antinodes can be computed by

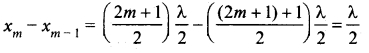
Similarly, the minimum of the amplitude A’ also occurs at some points in the space, and these points can be determined by setting
sin (kx) = 0 ⇒ kx = 0, π, 2π, 3π,…. = nπ
where n takes integer or integral values. Note that the elements at these points do not vibrate (not move), and the points are called nodes. The nth nodal positions is given by,
x_n = n\(\frac{λ}{2}\) where, n = 0,1,2,… …..(7)
For n = 0we have minimum at x₀ = 0
For n = 1 we have minimum at x₁ = \(\frac{λ}{2}\)
For n = 2 we have maximum at x₂ = λ and so on.
The distance between any two successive nodes can be calculated as
x_n – x_n-1 = n\(\frac{λ}{2}\) – (n – 1) \(\frac{λ}{2}\) = \(\frac{λ}{2}\)