You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Ex 4.2
Question 1.
The angles of a quadrilateral are in the ratio 2 : 4 : 5 : 7. Find all the angles.
Solution:
In a quadrilateral the angles add upto 360°.
Let’s call the angles 2x, 4x, 5x, 7x
2x + 4x + 5x + 7x = 360°
18x = 360°
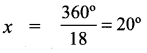
A = 2x = 2 × 20° = 40°
B = 4x = 4 × 20° = 80°
C = 5x = 5 × 20° = 100°
D = 7x = 7 × 20° = 140°
Question 2.
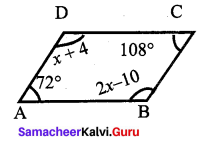
In a quadrilateral ABCD, ∠A = 12° and ∠C is the supplementary of ∠A. The other two angles are 2x – 10 and x + 4. Find the value of x and the measure of all the angles.
Solution:
∠A = 72°
∠C = 180° – 72° (∵ Supplementary at ∠A) = 108°
The other two angles are 2x – 10 and x + 4.
2x – 10 + x + 4 + 108° + 12° = 360°
3x + 174° = 360°
3x = 360° – 174°
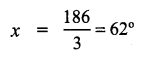
∴ ∠A = 72°
∠B = 2x – 10 = 2(62)- 10 = 124 – 10 = 114°
∠C = 108°
∠D = x + 4 = 62 + 4 = 66°
Question 3.
ABCD is a rectangle whose diagonals AC and BD intersect at O. If ∠OAB = 46°, find ∠OBC.
Solution:
∠ABC = 90°
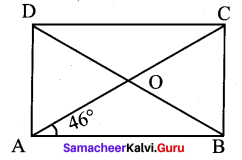
∠OAB + ∠OBC = 90°
46° + ∠OAB = 90°
∠OBC = 90° – 46° = 44°
Question 4.
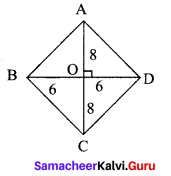
The lengths of the diagonals of a Rhombus are 12 cm and 16 cm. Find the side of the rhombus.
Solution:
Let ABCD be a rhombus with AC and BD as its diagonals.
We know that the diagonals of a rhombus bisect each other at right angles.
Let O be the intersecting point of both the diagonals
Let AC = 16 cm and BD = 12 cm
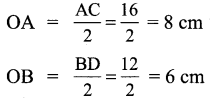
use Pythagoras theorem, we have
AB2 = OA2 + OB2
AB2 = 100
∴ AB = 10 cm
Question 5.
Show that the bisectors of angles of a parallelogram form a rectangle.
Solution:
Given ABCD is a parallelogram. Draw the angular bisectors AP, BP, CR and DR of the angles ∠A, ∠B, ∠C and ∠D respectively.
Now to prove : PQRS is a rectangle.
Proof: A rectangle is a parallelogram with one angle 90°.
First we will prove PQRS is a parallelogram.
Now AB || CD and AD is transversal. [ ∴ Interior angles on the same side of transversal are supplementary]
[Opposite sides of a parallelogram are parallel]
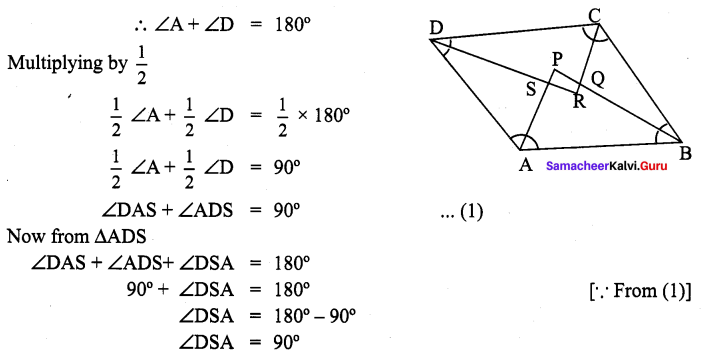
Also lines AP and DR intersects
So ∠PSR = ∠DS A
∴ ∠PSR = 90° [∵ Vertically opposite angles]
Similarly we can prove that ∠SPQ = 90°, ∠PQR = 90° and ∠SRQ = 90°
∴ ∠PSR = ∠PQR and ∠SPQ = ∠SRQ
∴ Both pair of opposite angles of PQRS is a parallelogram.
Also ∠PSR = ∠PQR = ∠SPQ = ∠SRQ = 90°
∴ PQRS is a parallelogram with one angle 90°.
∴ PQRS is a rectangle. Hence proved.
Question 6.
If a triangle and a parallelogram lie on the same base and between the same parallels, then prove that the area of the triangle is equal to half of the area of parallelogram.
Solution:
Given: ∆ABE and parallelogram ABCD have the same base and are between the same parallel lines (i.e) l1 || l2.
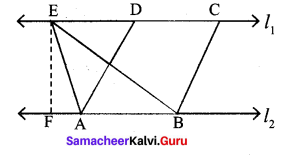
Perpendicular distance between l1 and l2 = P (say).
Prove that: area of (∆ABE) = \(\frac{1}{2}\) × area of the parallelogram ABCD
Proof: Area of ∆ABE = \(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\) × AB × (Perpendicular distance between l1
= \(\frac{1}{2}\) × AB × P ….(1)
Area of parallelogram ABCD = base × height.
∴ Area of parallelogram ABCD = AB × P …. (2)
From (1) and (2),
Area of ∆ABE = \(\frac{1}{2}\) × Area of parallelogram ABCD.
Hence proved.
Question 7.
Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in the figure. If a || b, c || d, e || f, find the marked angles between
(i) b and c
(ii) d and e
(iii) d and f
(iv) c and f.

Solution:
Since l, m are two parallel lines and PQ, RS, TU, VW are transversal.
Then ∠1 = ∠QOR [vertically opposite angles]
∠1 = 30° [∴ ∠QOR = 30°]
Also, PQ and TU are parallel and m and l are transversal.
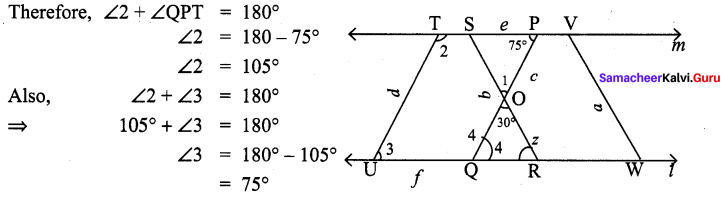
Also ∠3 + ∠4 = 180°
⇒ 75° + ∠4 = 180°
∠4 = 180° – 75° = 105°
Hence,
(i) 30°
(ii) 105°
(iii) 75°
(iv) 105°
Question 8.
In the given figure ∠A = 64° , ∠ABC = 58°. If BO and CO are the bisectors of ∠ABC and ∠ACB respectively of ∆ABC, find x° and y°.
Solution:
In ∆ABC, ∠A + ∠B + ∠C = 180°
⇒ 64° + 58° + ∠C = 180°
⇒ 122°+ ∠C = 180°
⇒ ∠C = 180°- 122° = 58°
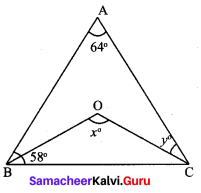
Also BO and CO are the bisectors of ∠ABC and ∠ACB respectively
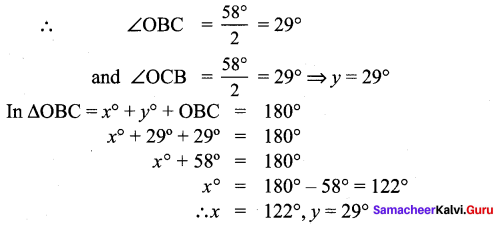
Question 9.
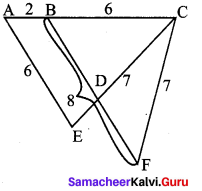
In the given Fig. if AB = 2, BC = 6, AE = 6, BF = 8, CE = 7, and CF = 7, compute the ratio of the area of quadrilateral ABDE to the area of ACDF.
Solution:
Given: AB = 2,
BC = 6,
AE = 6,
BF = 8,
CE = 7 and
CF = 7
Consider ∆AEC and ∆BCF,
In ∆AEC,
AC = 8,
AE = 6,
CE = 7
In ∆BCF,
BF = 8,
BC = 6,
CF = 7
∴ ∆AEC ≅ ∆BCF
∴ Area of ∆AEC = Area of ∆BCF
Subtract.area of ∆BDC both sides, we get
Area of ∆AEC – Area of ∆BDC = Area of ∆BCF – Area of ∆BDC
⇒ Area of quadrilateral ABDE = Area of ∆CDF
∴ The required ratio is 1 : 1
Question 10.
In the figure, ABCD is a rectangle and EFGH is a parallelogram. Using the measurements given in the figure, what is the length d of the segment that is perpendicular to \(\overline{\mathbf{H E}}\) and \(\overline{\mathbf{F G}}\) ?
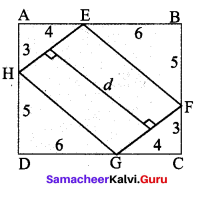
Solution:
Area of ABCD = length × breadth.
= DC × BC = 10 × 8 = 80.
Area of ∆AEH = Area of ∆CGF [since they are congruent by RHS rule]
Similarly, Area of ∆BEF = Area of ∆DGH
∴ Area of parallelogram = EFGH = Area of rectangle ABCD – 2(area of ∆AEH) – 2(area of ∆BEF)

Question 11.
In parallelogram ABCD of the accompanying diagram, line DP is drawn bisecting BC at N and meeting AB (extended) at P. From vertex C, line CQ is drawn bisecting side AD at M and meeting AB (extended) at Q. Lines DP and CQ meet at O. Show that the area of triangle QPO is \(\frac{9}{8}\) of the area of the parallelogram ABCD.
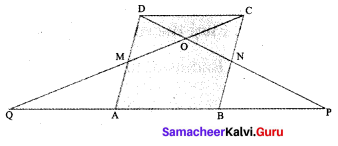
Solution:
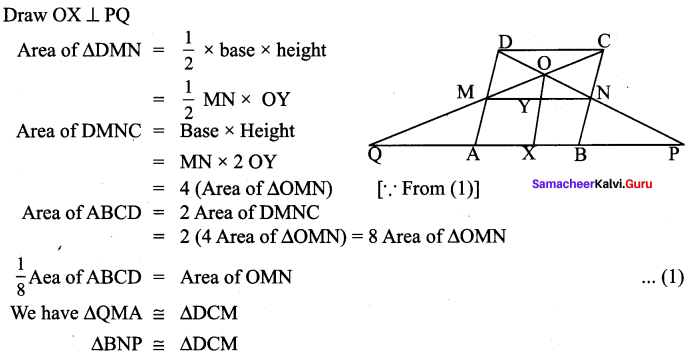
Area of ∆QDP = Area of ∆QMA + Area of ∆MNO + Area of MNBS + Area of ∆MAB
= Area of ∆DCM + Area of ∆MNO + Area of MNBA + Area of ∆NDC
= 2Area of ∆OMN + Area of ∆MNO + 4 Area of ∆OMN + 2 Area of ∆OMN
