Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.6

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.6

Question 1.
Factorise the following:
(i) x² + 10x + 24
(ii) z² + 4z – 12
(iii) p² – 6p – 16
(iv) t² + 72 – 17t
(v) y² – 16y – 80
(vi) a² + 10a – 600
Solution:
(i) x² + 10x + 24
x² + 10x + 24 = x² + 6x + 4x + 24

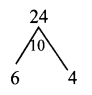
= x(x + 6) + 4 (x + 6)
= (x + 6) (x + 4)

(ii) z² + 4z – 12
z² + 4z – 12 = z² + 6z – 2z- 12

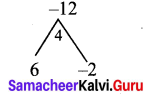
= z (z + 6) – 2 (z + 6)
= (z + 6) (z – 2)

(iii) p² – 6p – 16
p² – 6p – 16 = p² – 8p + 2p – 16

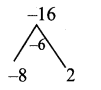
= p(p – 8) + 2(p – 8)
= (p – 8)(p + 2)

(iv) t² + 72 – 17t
t² + 72 – 17t = t² – 17t + 72
= t² – 9t – 8t + 72

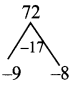
= t(t – 9) – 8 (t – 9)
= (t – 9) (t – 8)

(v) y² – 16y – 80
y² – 16y – 80 = y² – 20y + 4y – 80

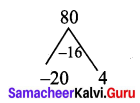
= y(y – 20) + 4 (y – 20)
= (y – 20) (y + 4)

(vi) a² + 10a – 600
a² + 10a – 600 = a² + 30a – 20a – 600

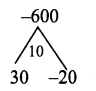
= a(a + 30) -20 (a + 30)
= (a + 30) (a – 20)

Question 2.
Factorise the following
(i) 2a² + 9a + 10
(ii) 5x² – 29xy – 42y²
(iii) 9 – 18x + 18x²
(iv) 6x² + 16xy + 8y²
(v) 12x² + 36x²y + 27y²x²
(vi) (a + b)² + 9 (a + b) + 18
Solution:
(i) 2a² + 9a + 10
2a² + 9a + 10 = 2a² + 4a + 5a + 10

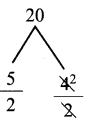
= 2a(a + 2) + 5 (a + 2)
= (a+ 2) (2a+ 5)

(ii) 5x² – 29xy – 42y²
5x² – 35xy + 6xy – 42y²

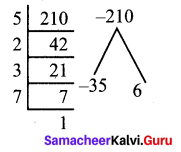
= 5x (x – 7) + 6y (x – 7)
= (x – 7) (5x + 6y)

(iii) 9 – 18x + 8x²
= 8x² – 18x + 9
= 8x² – 6x – 12x + 9

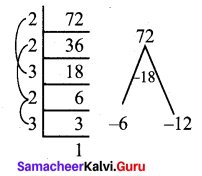
= 2x (4 x – 3) – 3 (4x – 3)
= (4x – 3) (2x – 3)

(iv) 6x² + 16xy + 8y²
= 2 (3x² + 8xy + 4y²)
= 2 (3x² + 8xy + 4y²)

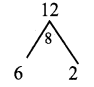
= 2 (3x² + 6xy + 2xy + 4y²)
= 2 (3x (x + 2y) + 2y (x + 2y))
= 2 (x + 2y) (3x + 2y)

(v) 12x² + 36x²y + 27y²x²
= 27y²x² + 36x²y + 12x² = 3x²(9y² + 12y + 4)

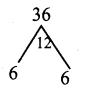
= 3x² (9y² + 6y + 6y + 4) = 3x² (3y (3y + 2) + 2 (3y + 2))
= 3x² (3y + 2) (3y + 2) = 3x² (3y + 2) (3y + 2)

(vi) (a + b)² + 9 (a + 6) + 18
= (a + b)² + 6 (a + b) + 3 (a + b) + 18

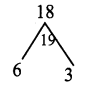
= (a + b) ((a + b) + 6) + 3 ((a + b) + 6)
= ((a + 6) + 6) ((a + b) + 3) = (a + b + 6) (a + b + 3)

Question 3.
Factorise the following:
(i) (p – q)² – 6(p – q) – 16
(ii) m² + 2mn – 24n²
(iii) \(\sqrt{5} a^{2}\) + 2a – \(3 \sqrt{5}\)
(iv) a⁴ – 3a² + 2
(v) 8m³ – 2m²n – 15mn²
(vi) \(\frac{1}{x^{2}}+\frac{1}{y^{2}}+\frac{2}{x y}\)
Solution:
(i) (p – q)² – 6 (p – q) – 16
= (p – q)² – 8(p – q) + 2(p – q) – 16

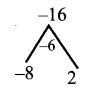
= (p – q)((p – q) – 8) + 2((p – q) – 8)
= (p – q – 8)(p – q + 2)

(ii) m² + 2mn – 24n²
= m² + 6mn – 4mn – 24n²

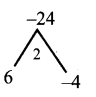
= m(m + 6n) – 4n(m + 6n)
= (m + 6n)(m – 4n)