You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 2 Real Numbers Ex 2.9
Multiple Choice Questions :
Question 1.
If n is a natural number then \(\sqrt{n}\) is
(1) always a natural number
(2) always an irrational number
(3) always a rational number
(4) may be rational or irrational
Solution:
(4) may be rational or irrational
Question 2.
Which of the following is not true?
(1) Every rational number is a real number.
(2) Every integer is a rational number.
(3) Every real number is an irrational number.
(4) Every natural number is a whole number.
Solution:
(3) Every real number is an irrational number
Hint:
Real numbers contain rationals and irrationals.
Question 3.
Which one of the following, regarding sum of two irrational numbers, is true?
(1) always an irrational number
(2) may be a rational or irrational number.
(3) always a rational number
(4) always an integer.
Solution:
(2) may be a rational or irrational number
Question 4.
Which one of the following has a terminating decimal expansion?

Solution:
(1) \(\frac { 5 }{ 64 }\)
Hint:
\(\frac { 5 }{ 64 }\) = \(\frac{5}{2^{6}}\)
![]()
Question 5.
Which one of the following is an irrational number?
(1) \(\sqrt { 25 }\)
(2) \(\sqrt { \frac { 9 }{ 4 } }\)
(3) \(\frac { 7 }{ 11 }\)
(4) π
Solution:
(4) π
Hint:
π represents a irrational number
Question 6.
An irrational number between 2 and 2.5 is
(1) \(\sqrt { 11 }\)
(2) \(\sqrt { 5 }\)
(3) \(\sqrt { 2.5 }\)
(4) \(\sqrt { 8 }\)
Solution:
(2) \(\sqrt { 5 }\)
Hint:
22 = 4 and 2.52 = 6.25
Question 7.
The smallest rational number by which – should be multiplied so that its decimal expansion terminates after one place of decimal is
(1) \(\frac { 1 }{ 10 }\)
(2) \(\frac { 3 }{ 10 }\)
(3) 3
(4) 30
Solution:
(2) \(\frac { 3 }{ 10 }\)
Hint:
\(\frac { 3 }{ 10 }\) is the small number.
Question 8.
If \(\frac { 1 }{ 7 }\) = \(0.\overline { 142857 }\) then the value of \(\frac { 5 }{ 7 }\) is
(1) \(0.\overline { 142857 }\)
(2) \(0.\overline { 714285 }\)
(3) \(1.\overline { 571428 }\)
(4) 0.714285
Solution:
(2) \(0.\overline { 714285 }\)
Hint:
5 × \(\frac { 1 }{ 7 }\) = 5 × \(0.\overline { 142857 }\) = \(0.\overline { 714285 }\)
![]()
Question 9.
Find the odd one out of the following.

Solution:
(4) \(\frac{\sqrt{54}}{\sqrt{18}}\)
Hint:
\(\sqrt { 72 }\) × \(\sqrt { 8 }\) = \(\sqrt { 9\times8 }\) × \(\sqrt { 8 }\) = 3 × 8 = 24
Question 10.
\(0.\overline { 34 }\) + \(0.3\overline { 4 }\) =
(1) \(0.6\overline { 87 }\)
(2) \(0.\overline { 68 }\)
(3) \(0.6\overline { 8 }\)
(4) \(0.68\overline { 7 }\)
Solution:
(1) \(0.6\overline { 87 }\)
Hint:
0.343434 … + 0.344444 … = \(0.6\overline { 87 }\)
Question 11.
Which of the following statement is false?
(1) The square root of 25 is 5 or -5
(2) \(\sqrt { 25 }\) = 5
(3) –\(\sqrt { 25 }\) = -5
(4) \(\sqrt { 25 }\)= ±5
Solution:
(4) \(\sqrt { 25 }\) = ±5
Question 12.
Which one of the following is not a rational number?
(1) \(\sqrt { \frac { 8 }{ 18 } }\)
(2) \(\frac { 7 }{ 3 }\)
(3) \(\sqrt { 0.01 }\)
(4) \(\sqrt { 13 }\)
Solution:
(4) \(\sqrt { 13 }\)
Hint:
(1) \(\sqrt { \frac { 8 }{ 18 } }\) = \(\sqrt { \frac { 4 }{ 9 } }\) = \(\frac { 2 }{ 3 }\) is a arational number
(2) \(\frac { 7 }{ 3 }\) is a rational number
(3) \(\sqrt { 0.01 }\) = \(\sqrt { \frac { 1 }{ 100 } }\) = \(\frac { 2 }{ 3 }\) is a rational number
(4) \(\sqrt { 13 }\) is a rational number
![]()
Question 13.
\(\sqrt { 27 }\) + \(\sqrt { 12 }\) =
(1) \(\sqrt { 39 }\)
(2) \(5\sqrt { 6 }\)
(3) \(5\sqrt { 3 }\)
(4) \(3\sqrt { 5 }\)
Solution:
(3) \(5\sqrt { 3 }\)
Hint:
\(\sqrt { 27 }\) + \(\sqrt { 12 }\) = \(\sqrt{9 \times 3}+\sqrt{4 \times 3}=3 \sqrt{3}+2 \sqrt{3}=5 \sqrt{3}\)
Question 14.
if \(\sqrt { 80 }\) = k\(\sqrt { 5 }\), then k =
(1) 2
(2) 4
(3) 8
(4) 16
Solution:
(2) 4
Hint: \(\sqrt { 80 }\) = \(\sqrt{16 \times 5}=4 \sqrt{5}=k \sqrt{5}\) ⇒ k = 4
Question 15.
\(4 \sqrt{7} \times 2 \sqrt{3}\) =
(1) 6\(\sqrt{10}\)
(2) 8\(\sqrt{21}\)
(3) 8\(\sqrt{10}\)
(4) 6\(\sqrt{21}\)
Solution:
(2) 8\(\sqrt{21}\)
Hint:
\(4 \sqrt{7} \times 2 \sqrt{3}\) = \(8\times\sqrt{7 \times 3}\) = 8\(\sqrt{21}\)
Question 16.
When written with a rational denominator, the expression \(\frac{2 \sqrt{3}}{3 \sqrt{2}}\) can be simplified as

Solution:
(3) \(\frac{\sqrt{6}}{3}\)
Hint:
\(\frac{2 \sqrt{3}}{3 \sqrt{2}}=\frac{2 \sqrt{3}}{3 \sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}=\frac{2 \sqrt{6}}{3 \times 2}=\frac{2 \sqrt{6}}{63}\)
Question 17.
When (2\(\sqrt{5}\) – \(\sqrt{2}\))2 is simplified, we get
(1) 4\(\sqrt{5}\) + 2\(\sqrt{2}\)
(2) 22 – 4\(\sqrt{10}\)
(3) 8 – 4\(\sqrt{10}\)
(4) 2\(\sqrt{10}\) – 2
Solution:
(2) 22 – 4\(\sqrt{10}\)
Hint:
(2\(\sqrt{5}\) – \(\sqrt{2}\))2 = (2\(\sqrt{5}\))2 – 2 × 2\(\sqrt{5}\) × \(\sqrt{2}\) + \(\sqrt{2^{2}}\)
= 4 × 5 – 4\(\sqrt{10}\) + 2 = 22 – 4\(\sqrt{10}\)
![]()
Question 18.
(0.000729)\(\frac{-3}{4}\) × (0.09)\(\frac{-3}{4}\) = ____.
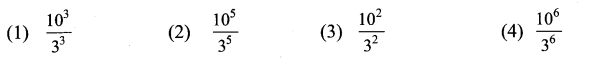
Solution:
(4) \(\frac{10^{6}}{3^{6}}\)
Hint :

Question 19.
If \( \sqrt{9^{x}}=\sqrt[3]{9^{2}}\) , than x = ___

Solution:
(2) \(\frac { 4 }{ 3 }\)
Hint:

Question 20.
The length and breadth of a rectangular plot are 5 x 105 and 4 x 104 metres respectively. Its area is .
(1) 9 × 101 m2
(2) 9 × 109 m2
(3) 2 × 1010 m2
(4) 20 × 1020 m2
Solution:
(3) 2 × 1010 m2
Hint:
l = 5 × 105 metres; b = 4 × 104 metres
∴ Area = l × b = 5 x 105 × 4 × 104
= 20 × 105+4= 20 × 109= 2.0 × 101 × 109 = 2 × 1010m2