You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 1 Set Language Ex 1.3
Question 1.
Using the given venn diagram, write the elements of
(i) A
(ii) B
(iii) A ∪ B
(iv) A ∩ B
(v) A – B
(vi) B – A
(vii) A’
(viii) B’
(ix) U
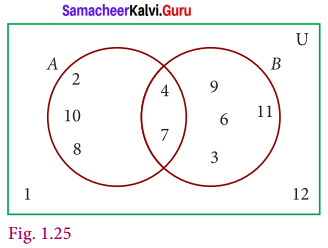
Solution:
(i) A = {2, 4, 7, 8, 10}
(ii) B = {3, 4, 6, 7, 9, 11}
(iii) A ∪ B = {2, 3, 4, 6, 7, 8, 9, 10, 11}
(iv) A ∩ B = {4, 7}
(v) A – B = {2, 8, 10}
(vi) B – A = {3, 6, 9, 11}
(vii) A’ = {1, 3, 6, 9, 11, 12}
(viii) B’ = {1, 2, 8, 10, 12}
(ix) U = {1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 12}.
Question 2.
Find A ∪ B, A ∩ B, A – B and B – A for the following sets.
(i) A = {2, 6, 10, 14} and B = {2, 5, 14, 16}
(ii) A = {a, b, c, e, u} and B = {a, e, i, o, u]
(iii) A = {x : x ∈ N, x ≤ 10} and B = {x : x ∈ W, x < 6}
(iv) A = Set of all letters in the word “mathematics” and B = Set of all letters in the word “geometry”
Solution:
(i) A = {2, 6, 10, 14} and B = {2, 5, 14, 16}
A ∪ B = {2, 6, 10, 14} ∪ {2, 5, 14, 16} = {2, 5, 6, 10, 14, 16}
A ∩ B = {2, 6, 10, 14} ∩ {2, 5, 14, 16} = {2, 14}
A – B = {2, 6, 10, 14} – {2, 5, 14, 16} = {6, 10}
B – A = {2, 5, 14, 16} – {2, 6, 10, 14} = {5, 16}
(ii) A = {a, b, c, e, u} and B = {a, e, i, o, u}
A ∪ B = {a, b, c, e, u) ∪ {a, e, i, o, u) = {a, b, c, e, i, o, u}
A ∩ B = {a, b, c, e, u} ∩ {a, e, i, o, u} {a, e, u}
A – B = {a, b, c, e, u) – {a, e, i, o, u) = {b, c}
B – A = {a, e, i, o, u} – {a, b, c, e, u} = {i, o}
(iii) x ∈ {1, 2, 3, ……..} ; x ∈ {0, 1, 2, 3, 4, 5, ……..}
A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
B = {0, 1, 2, 3, 4, 5}
A ∪ B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} ∪ {0, 1, 2, 3, 4, 5} = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A ∩ B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} ∩ {0, 1, 2, 3, 4, 5} = {1, 2, 3, 4, 5}
A – B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} – {0, 1, 2, 3, 4, 5} = {6, 7, 8, 9, 10}
B – A = {0, 1, 2, 3, 4, 5} – {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} = {0}
(iv) A= {m, a, t, h, e, i, c, s), B = {g, e, o, m, t, r, y)
A ∪ B = {m ,a, t, h, e, i, c, s} ∪ {g, e, o, m, t, r, y} = {m, a, t, h, e, i, c, s, g, o, r, y)
A ∩ B = {m, a, t, h, e, i, c, s} ∩ {g, e, o, m, t,r,y} = {m, t, e}
A – B = {m ,a, t, h, e, i, c, s} ∪ {g, e, o, m, t, r, y} = {a, h, i, c, s)
B – A = {m, a, t, h, e, i, c, 5} ∩ {g, e, o, m, t,r,y} = {g, o, r, y}
![]()
Question 3.
If U = {a, b, c, d, e,f g ,h}, A = {b, d, f, h} and B = {a, d, e, h}, find the following sets.
(i) A’
(ii) B’
(iii) A’ ∪ B’
(iv) A’ ∩ B’
(v) (A ∪ B)’
(vi) (A ∩ B)’
(vii) (A’)’
(viii) (B’)’
Solution:
(i) A’ = U – A = {a, b, c, d, e, f, g, y} – {b, d, f, h} = {a, c, e, g}
(ii) B’ = U – B = {a, b, c, d, e, f, g, y) – {a, d, e, h] = {b, c, f, g}
(iii) A’ ∪ B’= {a, c, e, g} ∪ {b, c, f, g} = {a, b, c, e, f g}
(iv) A’ ∩ B’= {a, c, e, g} ∩ {b, c, f, g} = {c, g}
(v) (A ∪ B)’ = U – (A ∪ B) = {a, b, c, d, e, f, g, y) – {a, b, d, e, f, h} = {c, g}
(vi) (A ∩ B)’ = U – (A ∩B) = {a, b, c, d, e, f, g, y} – {d, h} = {a, b, c, e, f, g}
(vii) (A’)’ = U – A’ = {a, b, c, d, e, f, g, h} – {a, c, e, g} = {b, d, f, h)
(viii) (B’)’ = U – B’ = {a, b, c, d, e, f, g, h} – {b, c, f, g} = {a, d, e, h}
Question 4.
Let U = {0, 1, 2 , 3, 4, 5, 6, 7}, A = {1, 3, 5, 7} and B = {0, 2, 3, 5, 7}, find the following sets.
(i) A’
(ii) B’
(iii) A ‘ ∪ B’
(iv) A’ ∩ B’
(v) (A ∪ B)’
(vi) (A ∩ B)’
(vii) (A’)’
(viii) (B’)’
Solution:
(i) A’ = U – A = {0, 1 ,2, y, 4, 5, 6, 7} – {1, 3, 5, 7} = {0, 2, 4, 6}
(ii) B’ = U – B = {0, 1, 2, 3, 4, 5, 6 ,7} – {0, 2, 3, 5, 7} = {1, 4, 6}
(iii) A’ ∪ B’ = {0, 2, 4, 6} ∪ {1, 4, 6} = {0, 1, 2, 4, 6}
(iv) A’ ∩ B’ = {0, 2, 4, 6} ∩ {1, 4, 6} = {4, 6}
(v) (A ∪ B)’ = U – (A ∪ B) = {0, 1, 2, 3, 4, 5, 6, 7} – {0, 1, 2, 3, 5, 7} = {4, 6}
(vi) (A ∩ B)’ = U – (A ∩ B)= {0, 1, 2, 3, 4, 5, 6, 7} – {3,5,7} = {0, 1, 2, 4, 6}
(vii) (A’)’ = U – A’ = {0, 1, 2, 3, 4, 5, 6, 7} – {0, 2, 4, 6} = {1, 3, 5, 7}
(viii) (B’)’ = U – B’ = {0, 1, 2, 3, 4, 5, 6, 7} – {1, 4, 6} = {0, 2, 3, 5, 7}.
Question 5.
Find the symmetric difference between the following sets.
(i) P = {2, 3, 5, 7, 11} and Q = {1, 3, 5, 11}
(ii) R = {l, m, n, o, p} and S = {j, l, n, q)
(iii) X = {5, 6, 7} and Y = {5, 7, 9, 10}
Solution:
(i) P = {2, 3, 5, 7, 11}
Q= {1, 3, 5, 11}
P – Q = {2, 3, 5, 7, 11} – {1, 3, 5, 11} = {2, 7}
Q – P = {1, 3, 5, 11} – {2, 3, 5, 7, 11} = {1}
P ∆ Q = (P – Q) ∪ (Q – P) = {2, 7} ∪ {1} = {1, 2, 7}
(ii) R = {l, m, n, o, p}
S = {j, l, n, q}
R – S = {l, m, n, o, p) – {j, l, n, q} = {m, o, p)
s – R = {j, l, n, q) – {l, m, n, o, p}= {j, q}
R ∆ S = (R – S) ∪ (S – R) = {m, o, p) ∪ {j, q} = {j, m, o, p, q)
(iii) X = {5, 6, 7}
Y = {5, 7, 9, 10}
X – Y = {5, 6, 7} – {5, 7, 9, 10} – {6}
Y – X = {5, 6, 9, 10} – {5, 6, 7} = {9, 10}
X ∆ Y = (X – Y) ∪ (Y – X) = {6} ∪ {9, 10} = {6, 9, 10}.
![]()
Question 6.
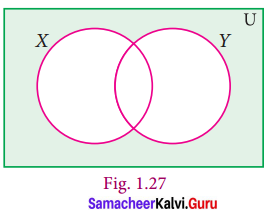
Using the set symbols, write down the expressions for the shaded region in the following
(i)
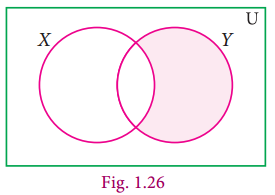
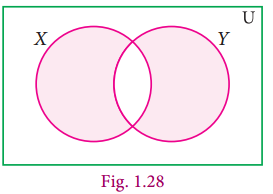
(ii)
(iii)
Solution:
(i) X – Y
(ii) (X ∪ Y)’
(iii) (X – Y) ∪ (X – Y)
Question 7.
Let A and B be two overlapping sets and the universal set U. Draw appropriate Venn diagram for each of the following,
(i) A ∪ B
(ii) A ∩ B
(iii) (A ∩ B)’
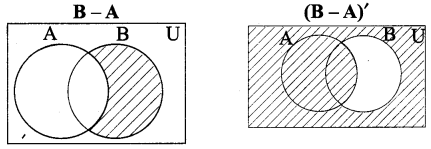
(iv) (B – A)’
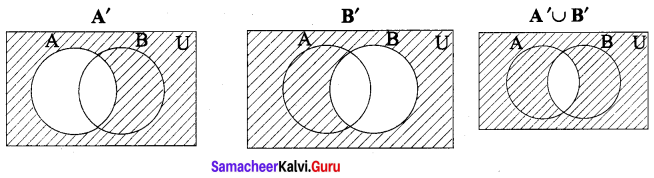
(v) A’ ∪ B’
(vi) A’ ∩ B’
(vii)What do you observe from the diagram (iii) and (v)?
Solution:
(i) A ∪ B
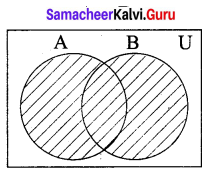
(ii) A ∩ B
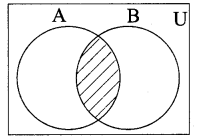
(iii) (A ∩ B)’
(iv) (B – A)’
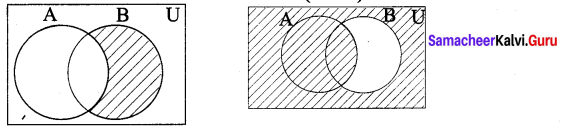
(v) A’ ∪ B’

(vi) A’ ∩ B’
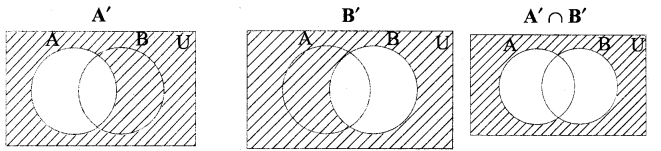
(vii) From the diagram (iii) and (v) we observe that (A ∩ B)’ = A’ ∪ B’.