You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 1 Set Language Additional Questions
Text Book Activities
Question 1.
Discuss and give as many examples of collections from your daily life situations, which are sets and which are not sets.
Solution:
Which are sets
- Collection of pen
- Collection of dolls
- Collection of books
- Collection of red flower etc.
Which are not sets
- Collection of good students in a class.
- Collection of beautiful flowers in a garden etc.
Question 2.
Write the following sets in respective forms.
Solution:

Question 3.
Fill in the blanks with appropriate cardinal numbers.
Solution:
![]()
Additional Questions and Answers
Exercise 1.1
Question 1.
Let A = {0, 1, 2, 3, 4, 5}. Insert the appropriate symbol G or g in the blank spaces,
(i) 0 ___ A
(ii) 6 ___ A
(iii) 3 ___ A
(iv) 4 ____ A
(v) 7 ____ A
Solution:
(i) 0 ∈ A
(ii) 6 ∉ A
(iii) 3 ∈ A
(iv) 4 ∈ A
(v) 7 ∉ A
Question 2.
Write the following in Set-Builder form.
(i) The set of all positive even numbers.
(ii) The set of all whole numbers less than 20.
(iii) The set of all positive integers which are multiple of 3.
(iv) The set of all odd natural numbers less than 15.
(v) The set of all letters in the word ‘computer’.
Solution:
(i) A = {x : x is a positive even number}
(ii) B = {x : x is a whole number and x < 20}
(iii) C = {x : x is a positive integer and multiple of 3}
(iv) D = {x : x is an odd natural number and x < 15}
(v) E = {x : x is a letter in the word “Computer”}
![]()
Question 3.
Write the following sets in Roster form.
(i) A = {x : x ∈ N, 2< x < 10 }
(ii) B = {x : x ∈ Z, –\(\frac { 1 }{ 2 }\) < x < \(\frac { 11 }{ 2 }\) }
(iii) C = {x : x is a prime number and a divisor of 6 }
(iv) x = {x : x = 2n, it n ∈ N and n ≤ 5}
(v) M = {x : x = 2y – 1, y ≤ 5, j ∈ W}
Solution:
(i) A = {3,4, 5, 6, 7, 8, 9}
(ii) B = {0, 1, 2, 3, 4, 5}
(iii) C = {2, 3}
(iv) Given, x = 2n, n ∈ N and n ≤ 5.
Here n = 1, 2, 3, 4, 5
n = 1 ⇒ 21 = 2
n = 2 ⇒ 22 = 4
n = 3 ⇒ 23 = 8
n = 4 ⇒ 24 = 16
n = 5 ⇒ 25 = 32
X = {2, 4, 8, 16, 32}
(v) Given, x = 2y – 1, y ≤ 5 and y ∈ W Here j = 0, 1,2, 3, 4, 5
y = 0 ⇒ x = 2 (0) – 1 = -1
y = 1 ⇒ x = 2 (1) – 1 = 2 – 1 = 1
y = 2 ⇒ x = 2 (2) – 1 = 4 – 1 = 3
y = 3 ⇒ x = 2 (3) – 1 = 6 – 1 = 5
y = 4 ⇒ x = 2 (4) – 1 = 8 – 1 = 7
y = 5 ⇒ x = 2 (5) – 1 = 10 – 1= 9
M = {-1, 1, 3, 5, 7, 9}
Therefore, we conclude that 2 and 19 are prime factors of 38.
Exercise 1.2
Question 1.
Find the number of subsets and number of proper subsets of a set X = {a, b, c, x, y, z}.
Solution:
Given X = {a, b, c, x, y, z}.
Then, n(X) = 6
The number of subsets = n[P(X)] = 26 = 64
The number of proper subsets = n[P(X)] – 1 = 26 – 1 = 64 – 1 = 63
Question 2.
Find the cardinal number of the following sets.
(i) A = {x : x is a prime factor of 12}.
(ii) B = {x : x ∈ W, x ≤ 5}.
(iii) X = {x : x is an even prime number}
Solution:
(i) Factors of 12 are 1, 2, 3, 4, 6, 12. So, the prime factors of 12 are 2,3.
We write the set A in roster form as A = {2, 3} and hence n(A) = 2.
(ii) In Tabular form B = {0, 1, 2, 3, 4, 5}
The set B has six elements and hence n(B) = 6
(iii) X = {2} [2 is the only even prime number]
∴ n (X) = 1
Question 3.
State whether the following sets are finite or infinite.
(i) A = {x : x is a multiple of 5, x ∈ N}.
(ii) B = {0,1, 2, 3, 4, 75}.
(iii) The set of all positive integers greater than 50.
Solution:
(i) A = {5, 10, 15, 20, …… } ∴A is an infinite set
(ii) Finite
(iii) Let X be the set of all positive integers greater than 50
Then X= (51, 52, 53, ….. }
∴ X is an infinite set.
Question 4.
Which of the following sets are equal?
(i) A = (1, 2, 3, 4}, B = {4, 3, 2, 1}
(ii) A = (4, 8, 12, 16}, B = (8, 4, 16, 18}
(iii) X ={2, 4, 6, 8}
Y = {x : x is a positive even integer and 0 < x < 10}
Solution:
(i) Since A and B contain exactly the same elements, A and B are equal sets.
(ii) A and B has different elements.
∴ A and B are not equal sets.
(iii) X = {2, 4, 6, 8}, Y = {2, 4, 6, 8}
∴ X and Y are equal sets.
Question 5.
Write ⊆ or ⊈ in each blank to make a true statement.
(i) {4, 5, 6, 7} ____ {4, 5, 6, 7, 8}
(ii) {a, b, c} ____ {b, e, f, g}
Solution:
(i) {4, 5, 6, 7} ⊈ {4, 5, 6, 7, 8}
(ii) {a, b, c} ⊈ {b, e, f, g}
![]()
Question 6.
Write down the power set of A= {3, {4, 5}}.
Solution:
The subsets of A are {Ø, {3}, {4, 5}, {3,{4, 5}}
P(A) = {Ø, {3}, {4,5}, {3{4,5}}
Exercise 1.3
Question 1.
Find the union of the following sets.
(i) A = {1, 2, 3, 5, 6} and B = {4, 5, 6, 7, 8}
(ii) X = {3, 4, 5} and Y = Ø
Solution:
(i) A ∪ B = {1, 2, 3, 4, 5, 6, 7, 8}
(ii) X ∪ Y = {3, 4, 5}
Question 2.
Find A ∩ B if (i) A = {10, 11, 12, 13}, B = {12, 13, 14, 15}, (ii) A = {5, 9, 11}, B = Ø.
Solution:
(i) A ∩ B = {12, 13}
(ii) A ∩ B = Ø
Question 3.
Given the sets A = {4, 5, 6, 7} and B = {1, 3, 8, 9}, find A ∩ B.
Solution:
A ∩ B = Ø
Question 4.
If A= {-2, -1, 0, 3, 4}, B = {-1, 3, 5}, find (i) A – B, (ii) B – A.
Solution:
(i) A – B = {-2, 0, 4}
(ii) B – A = {5}
Question 5.
If A = {2, 3, 5, 7,11} and B = {5, 7, 9, 11, 13}, find A ∆ B.
Solution:
A ∆ B= {2, 3, 9, 13}
Question 6.
Draw a venn diagram similar to one at the side and shade the regions representing the following sets (i) A’, (ii) B’, (iii) A’ ∪ B’, (iv) (A ∪ B)’, (v) A’ ∩ B’
Solution:
(i) A’
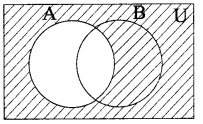
(ii) B’
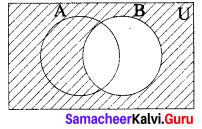
(iii) A’ ∪ B’
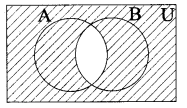
(iv) (A ∪ B)’
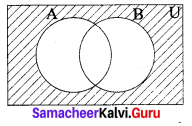
(v) A’ ∩ B’
Question 7.
State which of the following sets are disjoint.
(i) A = {2, 4, 6, 8}, B = {x : x is an even number < 10, x ∈ N}
(ii) X = {1, 3, 5, 7, 9}, Y = {0, 2, 4, 6, 8, 10}
(iii) R = {a, b, c, d, e}, S = {d, e, b, c, a}
Solution:
(i) A = {2, 4, 6, 8}, B = {2, 4, 6, 8}
A ∩ B = {2, 4, 6, 8} ≠ Ø
∴ A and B are not disjoint sets.
(ii) X ∩ Y = { } = Φ, X and Y are disjoint sets.
(iii) R ∩ S = {a, b, c, d, e} ≠ Ø
∴ R and S are not disjoint sets.
![]()
Question 8.
If A = {a, b, c, d, e}and B = {a, e, i, o, u} find AB.
Solution:
A ∩ B = {a, b, c, d, e} ∩ {a, e, i, o, u} = {a, e}
Exercise 1.4
Question 1.
If A and B are two sets containing 13 and 16 elements respectively, then find the minimum and maximum number of elements in A ∪B?
Solution:
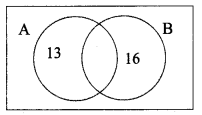
n(A) = 13 ; n(B) = 16
Minimum n(A ∪ B) = 16
Maximum n(A ∪ B) = 13 + 16 = 29
Question 2.
If n(U) = 38, n(A) = 16, n(A ∩ B) = 12, n(B’) = 20, find n(A ∪ B).
Solution:
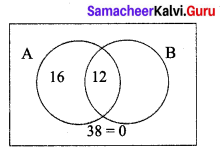
n(U) = 38
n(A) = 16
N(A ∩ B) = 12
n(B’) = 20
n(A ∪ B) = ?
Hint: n(B) = n(U) – n(B)’
n(B) = 38 – 20
n(B) = 18
n(A ∪ B) = n(A) + n(B) – n (A ∩ B)
n(A ∪ B) = 16 – 12 + 18
n(A ∪ B) = 4 + 18 = 22.
Question 3.
Let A = {b, d, e, g, h} and B = {a, e, c, h} verify that n(A – B) = n(A) – n(A ∩ B)
Solution:
A = {b, d, e, g, h),
B = {a, e, c, h}
A ∩ B = {b, d, g}
n(A ∩ B) = 3 ………….. (1)
A ∩ B = {e, h}
n(A ∩ B) = 2, n(A) = 5
n(A) – n(A ∩ B) = 5 – 2 = 3 ……………… (2)
Form (1) and (2) we get
n(A – B) = n(A) – n(A ∩ B)
Question 4.
If A = {2, 5, 6, 7} and B = {3, 5, 7, 8}, then verify the commutative property of
(i) union of sets
(ii) intersection of sets
Solution:
Given, A = {2, 5, 6, 7} and B = {3, 5, 7, 8}
(i) A ∪ B = {2, 3, 5, 6, 7, 8} ……………. (1)
B ∪ A = {2, 3, 5, 6, 7, 8} …………… (2)
From (1) and (2) we have A ∪ B = B ∪ A
It is verified that union of sets is commutative.
(ii) A n B = {5, 7} …………… (3)
B n A = {5, 7} ……………. (4)
From (3) and (4) we get, A ∩ B = B ∩ A
It is verified that intersection of sets is commutative.
![]()
Question 5.
If A = {b, c, d, e} and B = {b, c, e, g} and C = {a, c, e}, then verify A ∪ (B ∪ C) = (A ∪ B) ∪ C.
Solution:
Given, A = {b, c, d, e} and B = {b, c, e, g} and C = {a, c, e}
Now B ∪ C = {a, b, c, e, g}
Au(B ∪C) = {a, b, c, d, e, g} ……………. (1)
Then, A ∪ B = {b, c, d, e, g}
(A ∪ B) ∪ C = {a, b, c, d, e, g} ……………… (2)
From (1) and (2) it is verified that
A ∪ (B ∪ C) = (A ∪ B) ∪ C
Exercise 1.5
Question 1.
If A = {1, 3, 5, 7, 9}, B = {x : x is a composite number and x < 12} and C = {x : x ∈ N and 6 < x < 10} then verify A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C).
Solution:
Given, A = {1, 3, 5, 7, 9} and B = {4, 6, 8, 9, 10}and C = {6, 7, 8, 9}
B ∩ C = {4, 6, 8, 9, 10} n {6, 7, 8, 9} = {6, 8, 9}
A ∪ (B ∩ C) = {1, 3, 5, 6, 7, 8, 9} ……………. (1)
Then (A ∪ B) = {1, 3, 5, 7, 9} ∪ {4, 6, 8, 9, 10} = {1, 3, 4, 5, 6, 7, 8, 9, 10}
(A ∪ C) = {1, 3, 5, 7, 9} ∪ {6, 7, 8, 9} = {1,3, 5, 6, 7, 8, 9}
(A ∪ B) ∩ (A ∪ C) = {1, 3, 4, 5, 6, 7, 8, 9, 10} ∩ {1, 3, 5, 6, 7, 8, 9}
= {1, 3, 5, 6, 7, 8, 9} …………….. (2)
From (1) and (2), it is verified that
A ∪ (B ∩C) = (A ∪ B) ∩ (A ∪ C)
Question 2.
If A, B and C are overlapping sets, draw venn diagram for : A ∩ B
Solution:
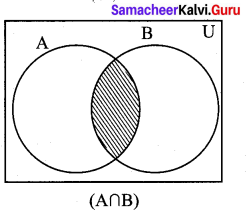
Question 3.
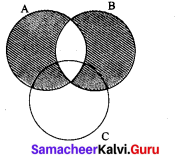
Draw Venn diagram for A ∩ B ∩ C
Solution:
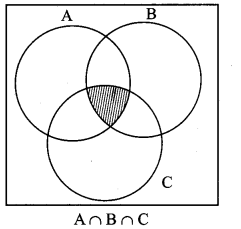
Question 4.
If P = {x : x ∈ N and 1 < x < 11}, Q = {x : x = 2n, n ∈ N and it < 6} and R = {4, 6, 8, 9, 10, 12}, then verify P – (Q ∩ R) = (P – Q) ∪ (P – R).
Solution:
The roster form of sets P, Q and R are P = {2, 3, 4, 5, 6, 7, 8, 9, 10}, Q = {2, 4, 6, 8, 10} and R = {4, 6, 8, 9, 10, 12}
First, we find Q ∩ R = {4, 6, 8, 10}
Then, P – (Q ∩ R) = {2, 3, 5, 7, 9} ………….. (1)
Next, P – Q = {3, 5, 7, 9}
and P – R = {2, 3, 5, 7}
and so, (P – Q) ∪ (P – Q) = {2, 3, 5, 7, 9} ……………. (2)
Hence from (1) and (2), it verified that P – (Q ∩ R) = (P – Q) ∪ (P – R)
Finding the elements of set Q
Given, x = 2 n
n = 1 → x = 2 (1) = 2
n = 2 → x = 2(2) = 4
n = 3 → x = 2 (3) = 6
n = 4 → x = 2(4) = 8
n = 5 → x = 2(5) = 10
Therefore, x takes values such as 2, 4, 6, 8, 10
![]()
Question 5.
If U = {x : x ∈ Z, -3 < x ≤ 9}, A = {x : x = 2P + 1, P ∈ Z , -2 ≤ P ≤ 3}, B = {x : x = q + l, q ∈ Z, 0 ≤ q ≤ 3}, verify De Morgan’s laws for complementation.
Solution:
Given, U = {-3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
A = {-3, -1, 1, 3, 5, 7} and B = {1, 2, 3, 4}
Law (i) (A ∪ B)’ = A’ ∩ B’
Now, A ∪ B = {-3, -1, 1, 2, 3, 4, 5, 7}
(A ∪ B)’ = {-2, 0, 6, 8, 9} ………….. (1)
Then, A’ = {-2, 0, 2, 4, 6, 8, 9) and
B’ = {-3, -2, -1, 0, 5, 6, 7, 8, 9}
A’ ∩ B’ = {-2, 0, 6, 8, 9} ……………… (2)
From (1) and (2) it is verified that
(A ∪ B)’ = A’ ∩ B’
Law (ii) (A ∩ B)’ = A’ ∪ B’
Now, A ∩ B = {1, 3}
(A ∩ B)’ = {-3, -2, -1, 0, 2, 4, 5, 6, 7, 8, 9} ………….. (3)
Then, A’ ∪ B’ = {-3, -2, -1, 0, 2, 4, 5, 6, 7, 8, 9} ………………. (4)
From (3) and (4) it is verified that
(A ∩ B)’ = A’ ∪ B’
Exercise 1.6
Question 1.
From the given venn diagram. Find (i) A, (ii) B, (iii) A ∪ B (iv) A ∩ B also verify that n(A ∪B) = n(A) + n(B) – n(A ∩ B).
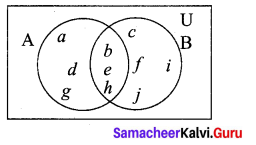
Solution:
A = {a, b, d, e, g, h}
B = {b, c, e, f, h, i, j}
A ∪ B = {a, b, c, d, e, f, g, h, i, j}
A ∩ B = {b, e, h}
So, n(A) = 6, n(B) = 7, n(A ∪B) = 10, n(A ∩ B) = 3
Now, n(A) + n(B) – n(A ∩ B) = 6 + 7 – 3 = 10
Hence, n(A) + n(B) – n(A ∩ B) = n(A ∪ B)
Question 2.
If n(A) = 12, n(B) = 17 and n(A ∪ B) = 21, find n(A ∩B).
Solution:
Given that n(A) = 12, n(B) = 17 and n(A ∪ B) =21
By using the formula n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
n(A ∩ B) = 12 + 17 – 21 = 8
Question 3.
In a school, 80 students like Maths, 90 students like Science, 82 students like History, 21 like both Maths and Science, 19 like both Science and History 20 like both Maths and History and 8 liked all the three subjects. If each student like atleast one subject, then find (i) the number of students in the school (ii) the number of students who like only one subject.
Solution:
Let M, S and H represent sets of students who like Maths, Science and History respectively.
Then, n(M) = 80, n(S) = 90, n(H) = 82, n(M ∩ S) = 21, n(S ∩ H) = 19, n(M ∩ H) = 20, n(M ∩ S ∩ H) = 8
Let us represents the given data in a venn diagram.
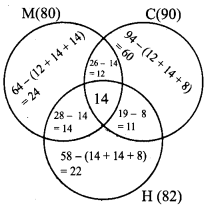
(i) The number of student in the school = 52 + 59 + 55 + 12 + 11 + 8 + 8 = 205
(ii) The number of students who like only one subject = 52 + 59 + 55 = 166
Question 4.
State the formula to find n(A ∪ B ∪ C).
Solution:
n( A ∪ B ∪ C) = n(A) + n(B) +n(C) – n(A ∩ B) – (B ∩ C) – n(A ∩ C) + (A ∩ B ∩ B)
![]()
Question 5.
Verify n (A ∪ B ∪ C) = n (A) + n(B) + n (C) – n(A ∩ B) – (B ∩ C) – n(A ∩ C) + (A ∩ B ∩ C) for the following sets A = {1, 3, 5, 6, 8}, B = {3, 4, 5, 6} and C = {1, 2, 3, 6}
Solution:
(A ∪ B ∪ C) = {1,2, 3, 4, 5, 6, 8}
n (A ∪ B ∪ C) = 7
Also, n (A) = 5, n (B) = 4, n (C) = 4,
Further, A ∩ B = {3, 5, 6} ⇒ n(A ∩ B) = 3
B ∩ C = {3, 6} ⇒ n(B ∩ C) = 2
A ∩ C = {3, 5, 6} ⇒ n(A ∩ C) = 3
Also, A ∩ B ∩ C = {3, 6} ⇒ n(A ∩ B ∩ C) = 2
Now n (A ∪ B ∪ C) = n (A) + n (B) + n (C) – n(A ∩ B) – n( B ∩ C) – n (A ∩ C) + n(A ∩ B ∩ C)
7 = 5 + 4 + 4 – 3 – 2 – 3 + 2
7 = 13 – 8 + 2
7 = 5 + 2
7 = 7
Thus verified
Exercise 1.7
Multiple Choice Questions
Question 1.
If A = {5, {5, 6}, 7} which of the following is correct?
(1) {5, 6} ∈ A
(2) {5} ∈ A
(3) {7} ∈ A
(4) {6} ∈ A
Solution:
(1) {5, 6} ∈ A
Hint: {5, 6} is an element of A.
Question 2.
If x = {a, {b, c}, d}, which of the following is a subset of X?
(1) {a, b}
(2) {b, c}
(3) {c, d}
(4) {a, d}
Solution:
(4) {a, d}
Hint: b is not an element of X. Similarly c.
Question 3.
If a finite set A has m elements, then the number of non-empty proper subset of A is
(1) 2m
(2) 2m – 1
(3) 2m-1
(4) 2(2m-1 – 1)
Solution:
(4) 2(2m-1 – 1)
Hint: P(A) = 2m Proper non empty subset = 2m – 2 = 2 (2m-1 – 1)
Question 4.
For any three A, B and C, A – (B ∪ C) is
(1) (A – B) ∪ (A – C)
(2) (A – B) ∩ (A ∪ C)
(3) (A – B) ∪C
(4) A ∪ (B – C)
Solution:
(2) (A – B) ∩ (A ∪ C)
Question 5.
Which of the following is true?
(1) (A ∪ B) = B ∪ A
(2) (A ∪ B)’ = A’ – B’
(3) (A ∩ B)’ = A’ ∩ B’
(4) A – (B ∩ C) = (A – B) ∩ (A – C)
Solution:
(1) (A ∪ B) = B ∪ A
![]()
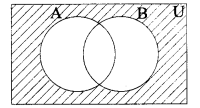
Question 6.
The shaded region in the venn diagram is
(1) A ∪ B
(2) A ∩ B
(3) (A ∩ B)’
(4) (A – B) ∪ (B – A)
Solution:
(4) (A – B) ∪ (B – A)
Hint: