You can Download Samacheer Kalvi 8th Science Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 8th Science Solutions Term 1 Chapter 1 Measurement
Samacheer Kalvi 8th Science Measurement Text Book Exercises
I. Choose the best answer
Question 1.
Which one the following system of units is the British System of unit?
(a) CGS
(b) MKS
(c) FPS
(d) SI
Answer:
(c) FPS
Question 2.
Electric current belongs to …………… quantities
(a) Base
(b) Supplementary
(c) Derived
(d) professional
Answer:
(a) Base
Question 3.
SI unit of temperature is
(a) Celsius
(b) Fahrenheit
(c) kelvin
(d) Ampere
Answer:
(c) kelvin
![]()
Question 4.
Amount of substance is
(a) Directly proportional to the number of atoms
(b) Inversely proportional to the number of atoms
(c) Directly proportional to the square of number of atoms
(d) Inversely proportional to the square of number of atoms
Answer:
(a) directly proportional to the number of atoms
Question 5.
Luminous intensity is the intensity of
(a) Laser light
(b) UV light
(c) Visible light
(d) IR light
Answer:
(c) visible light
Question 6.
Which one of the following devices is used to measure electric current
Answer:

Question 7.
SI unit stands for
(a) International system of units
(b) Integrated System of units
(c) International symbol of units
(d) Integrated symbol of units
Answer:
(a) International system of units
Question 8.
Closeness of two or more measured values is called as
(a) Accuracy
(b) Precision
(c) Error
(d) Approximation
Answer:
(b) Precision
![]()
Question 9.
Quantities other than base quantities are called as
(a) Supplementary quantities
(b) Derived quantities
(c) Professional quantities
(d) Energy quantities
Answer:
(b) Derived quantities
Question 10.
Which of the following statements about approximation is wrong?
(a) Approximation gives accurate value.
(b) Approximation simplifies the calculation.
(c) Approximation is very useful when little information is available.
(d) Approximation gives the nearest value only.
Answer:
(a) Approximation gives accurate value.
II. Fill in the blanks
- The solid angle is measured in ……………
- …………….. recognized the need of ‘Standard Units’ for physical quantities.
- The coldness or hotness of a substance is expressed by ……………..
- …………….. is used to measure electric current.
- ……………… of substance, contains 6.023 x 10+23 atoms or molecules.
- Luminous Intensity is the amount of visible light, that is emitted in unit area per unit …………….
- Quartz clock uses …………….. oscillations.
- The uncertainty in measurement is called as …………….
- ……………… is the closeness of the measured value to the original value.
- The intersection of two straight lines gives us ……………….
Answer:
- Steradian
- Scientists
- Temperature
- Ammeter
- One mole
- Solid angle
- Electronic
- Error
- Accuracy
- plane angle
III. True or False
Question 1.
SI units are metric system of units.
Answer:
True
Question 2.
Temperature is a measure of total kinetic energy of the particles in a system.
Answer:
False
Correct statement:
Temperature is a measure of average kinetic energy of the particles in a system.
Question 3.
In thermometers, freezing point of water is taken as the Upper Fixed Point.
Answer:
False
Correct statement:
In thermometers, boiling point of water is taken as the Upper Fixed Point.
Question 4.
One coulomb of charge flowing per minute is called ‘ampere’.
Answer:
False
Correct statement:
One coulomb of charge flowing per second is called ‘ampere’.
![]()
Question 5.
Amount of substance gives the number of particles present in the substance.
Answer:
True
Question 6.
Intensity of light from a candle is approximately equal to one ‘candela’.
Answer:
True
Question 7.
Angle formed at the top of a cone is an example of ‘Plane Angle’.
Answer:
True
Question 8.
Quartz clocks are used in GPS Devices.
Answer:
False
Correct statement:
Atomic clocks are used in GPS Devices.
Question 9.
Candela is used to express electric field intensity.
Answer:
False
Correct statement:
Candela is used to express luminous intensity.
Question 10.
The number 4.582 can be rounded off as 4.58.
Answer:
True
IV. Match the following
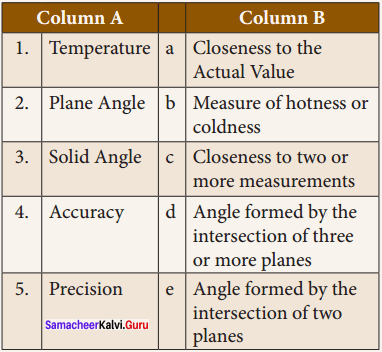
Answer:
- b
- e
- d
- a
- c
V. Assertion & Reason
Question 1.
Direction: Mark the correct choice as
(a) If both assertion and reason are true and reason is the correct explanation of the assertion.
(b) If both assertion and reason are true but reason is not the correct explanation of the assertion.
(c) Assertion is true, but reason is false.
(d) Assertion is false, but reason is true.
Question 1.
Assertion : The SI system of units is the suitable system for measurements.
Reason : The SI unit of temperature is kelvin.
Answer:
(b) Both assertion and reason are true but reason is not the correct explanation of the assertion
Correct explanation :
In SI system the units are precisely defined and have the same value everywhere.
![]()
Question 2.
Assertion : Electric current, amount of substance, Luminous Intensity are the fundamental physical quantities.
Reason : They are independent of each other.
Answer:
(a) Both assertion and reason are true and reason is the correct explanation of the assertion
Question 3.
Assertion : The seconds hand of a clock is having least count of one second.
Reason : Least count is the maximum measurement that can be measured accurately by an instrument.
Answer:
(c) Assertion is true, but reason is false
Correct explanation :
Least count is the minimum measurement that can be measured accurately by an instrument.
Question 4.
Assertion : Avogadro’s number is the number of atoms in one mole of substance.
Reason : Avogadro’s number is a constant.
Answer:
(a) Both assertion and reason are true and reason is the correct explanation of the assertion
Question 5.
Assertion : Radian is the unit of solid angle.
Reason : One radian is the angle subtended at the centre of a circle by an arc of length equal to its radius.
Answer:
(d) Assertion is false, but reason is true]
Correct explanation :
Radian is the unit of plane angle.
VI. Answer in a word or two (Very Short Answer)
Question 1.
What is the unit of mass in FPS system?
Answer:
Pound.
Question 2.
How many base quantities are included in SI system?
Answer:
Seven.
Question 3.
Give the name of the instrument used for the measurement of temperature.
Answer:
Thermometer.
![]()
Question 4.
What is the ‘Lower Fixed Point’ of the Fahrenheit scale?
Answer:
32°F.
Question 5.
What is the SI unit of Luminous Intensity?
Answer:
Candela (cd).
Question 6.
What is the value of Avogadro’s number?
Answer:
6.023 x 1023.
Question 7.
What type of oscillations are used in atomic clocks?
Answer:
Periodic vibrations.
Question 8.
Mention the types of clocks based on their display.
Answer:
Analog clock and digital clock.
Question 9.
How many times will the ‘minute hand’ rotate in one hour?
Answer:
One time.
Question 10.
How many hours are there in a minute?
Answer:
60 minutes = 1 hr
1 minute = \(\frac { 1 }{ 60 }\) = 0.0167 hours.
VII. Answer the Questions given below (Short Answer)
Question 1.
What is measurement?
Answer:
Measurement is the process of finding an unknown physical quantity by using a standard quantity.
Question 2.
Name some common systems of measurement.
Answer:
Some common systems of units are:
- FPS – System (Foot for length, Pound for mass and Second for time)
- CGS – System (Centimetre for length, Gram for mass and Second for time)
- MKS – System (Metre for length, Kilogram for mass and Second for time)
Question 3.
Define – Temperature.
Answer:
Temperature is a measure of the average kinetic energy of the particles in a system.
Question 4.
Define – ampere.
Answer:
One ampere is defined as one ‘coulomb’ of charge moving in a conductor in one second.
![]()
Question 5.
What is electric current?
Answer:
The magnitude of an electric current is the amount of electric charges flowing through a conductor in one second.
Question 6.
What is luminous Intensity?
Answer:
The measure of the power of the emitted light, by a light source in a particular direction, per unit solid angle is called as luminous intensity.
Question 7.
Define – mole.
Answer:
Mole is defined as the amount of substance, which contains 6.023 x 1023 entities.
Question 8.
What are the differences between Plane angle and solid angle?
Answer:
Difference between Plane Angle and Solid Angle:
Plane Angle:
- Angle between the intersection of two lines or planes.
- It is two dimensional
- Unit is radian.
Solid Angle:
- Angle between the intersection of three or more planes at a common point.
- It is three dimensional.
- Unit is steradian.
Question 9.
What are errors?
Answer:
The value of every measurement contains some uncertainty. These uncertainties are called as ‘Errors’.
VIII. Answer in detail
Question 1.
List out the base quantities with their units.
Answer:
Base Quantities and Units:

Question 2.
Write a short note on different types of clocks.
Answer:
Types of clocks based on display:
- Analog clocks
- Digital clocks
1. Analog clocks:
It looks like a classic clock. It has three hands to show the time.
- Hours Hand : It is short and thick. It shows ‘hour’.
- Minutes Hand : It is long and thin. It shows ‘minute’.
- Seconds Hand : It is long and very thin. It shows ‘second’. It makes one rotation in one minute and 60 rotations in one hour.
Analog clocks can be driven either mechanically or electronically.

2. Digital clocks:
- A digital clock displays the time directly. It shows the time in numerals or other
symbols. It may have a 12 hours or 24 hours display. - Recent clocks are showing Date, Day, Month, Year, Temperature etc.
- Digital clocks are often called as Electronic Clocks.
Différent types of clocks based on working mechanism:
1. Quartz Clock:
- These clocks are activated by ‘electronic oscillations’, which are controlled by a ‘quartz crystal’.
- The frequency of a vibrating crystal is very precise. So, the quartz clock is more accurate than the mechanical clock.
- These clocks have an accuracy of one second in every 109 seconds.

2. Atomic Clock:
- These clocks are making use of periodic vibrations occurring within the atom.
- These clocks have an accuracy of one second in every 10b seconds.
- Atomic clocks are used in Global Positioning System (GPS), Global Navigation Satellite System (GLONASS) and International time distribution services.

IX. Higher Order Thinking Question
Question 1.
Your friend was absent yesterday. You are enquiring about his absence. He told, he was affected by a fever of 100°C and went to a hospital for treatment. Is it possible of 100°C fever? If it is wrong, try to make him to understand his mistake.
Answer:
- No. It is not possible of 100°C fever. The normal temperature of human body is between 98.4°F and 98.6°F.
- So, he should say that, he was affected by a fever of 100°F and it is not 100°C.
Samacheer Kalvi 8th Science Solutions Measurement Additional Questions
I. Choose the correct answer
Question 1.
The SI unit of length is the ……………….
(a) Millimetre
(b) Centimetre
(c) Metre
(d) kilometre
Answer:
(c) Metre
Question 2.
The magnitude of a physical quantity consists of ……………..
(a) A unit
(b) A number and a unit
(c) A number
(d) Unit and its symbol
Answer:
(b) A number and a unit
Question 3.
The SI unit of mass is ……………..
(a) Milligram
(b) Gram
(c) Quintal
(d) kilogram
Answer:
(d) kilogram
![]()
Question 4.
Among the following, which is not an metric system?
(a) CGS
(b) MKS
(c) FPS
(d) SI
Answer:
(c) FPS
Question 5.
……………. is a physical quantity that expresses the degree of hotness or coldness of a substance.
(a) Electric current
(b) Luminous intensity
(c) Temperature
(d) None of the above
Answer:
(c) Temperature
II. Fill in the Blanks
- ……………… is the process of finding an unknown physical quantity by using a standard quantity.
- The CGS, MKS and SI units are system of units.
- FPS is a …………… system of units.
- Temperature is a measure of the average ……………. of the particles in a system
- Melting point of pure ice (0° C) is taken as ……………… fixed point.
Answer:
- Measurement
- Metric
- British
- kinetic energy
- Lower
III. True or False – if false give the correct statement
Question 1.
The unit of length in FPS system is foot.
Answer:
True.
Question 2.
The unit of mass in CGS system is kilogram.
Answer:
False
Correct statement:
The unit of mass in CGS system is gram.
Question 3.
Heat is a physical quantity that expresses the degree of hotness or coldness of a substance.
Answer:
False
Correct statement:
Temperature is a physical quantity that expresses the degree of hotness or coldness of a substance.
Question 4.
Heat removed from a substance will lower its temperature.
Answer:
True
Question 5.
In thermometers, boiling point of water (100° C) is taken as upper fixed point.
Answer:
True.
![]()
Question 6.
Normal temperature of the human body is between 98.4° C and 98.6° C.
Answer:
False
Correct statement:
Normal temperature of the human body is between 98.4° F and 98.6° F.
Question 7.
Voltmeter is a device used to measure electric current.
Answer:
False
Correct statement:
Ammeter is a device used to measure electric current.
Question 8.
The super conductors are used to levitate trains from the track.
Answer:
True
IV. Match the following
Question 1.
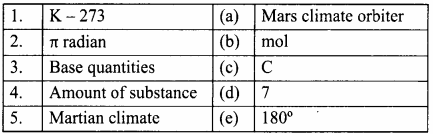
Answer:
- c
- e
- d
- b
- a
Question 2.
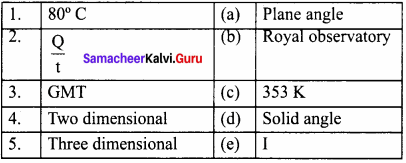
Answer:
- c
- e
- b
- a
- d
V. Assertion and Reason.
Question 1.
Mark the correct choice as:
(a) If both assertion and reason are true and the reason is the correct explanation of the assertion.
(b) If both assertion and reason are true, but the reason is not the correct explanation of the assertion.
(c) If the assertion is true, but the reason is false.
(d) If the assertion is false, but the reason is true.
Question 1.
Assertion : The SI unit of temperature is kelvin.
Reason : Thermometers are calibrated with some standard scales like Celsius, fahrenheit and kelvin.
Answer:
(b) Both assertion and reason are true, but the reason is not the correct explanation of the assertion
Question 2.
Assertion : Temperature is a physical quantity.
Reason : Temperature is the degree of hotness or coldness of a body.
Answer:
(a) Both assertion and reason are true and the reason is the correct explanation of the assertion
Question 3.
Assertion : Radian is the angle subtended at the centre of a circle by an arc whose length is equal to the radius of the circle.
Reason : 1 radian = \(\frac { 180 }{ π }\)
Answer:
(a) Both assertion and reason are true and the reason is the correct explanation of the assertion
VII. Very short Answers
Question 1.
What is physics?
Answer:
Physics is the study of nature and natural phenomena.
Question 2.
Name the British system of units.
Answer:
FPS system.
Question 3.
How many base quantities are there?
Answer:
Seven.
![]()
Question 4.
What is the symbol for unit of electric current?
Answer:
A (ampere).
Question 5.
Mention the SI unit of luminous flux.
Answer:
Lumen.
VII. Short Answers
Question 1.
Mention the SI unit & symbol of temperature.
Answer:
- The SI unit of Temperature is kelvin.
- It’s symbol is ‘K’.
Question 2.
Write any 2 applications of various thermometric scales.
Answer:
- Physicians use ‘clinical thermometers’. It is graduated in ‘Fahrenheit Scale’
- Scientists are using thermometers with kelvin scale.
![]()
Question 3.
Define electric current. Write its formula and unit.
Answer:
1. The magnitude of an electric current is the amount of electric charges flowing through a conductor in one second.
Electric current = \(\frac { Amount of electric charges (Q) }{ time (t) }\)
I = \(\frac { Q }{ t}\)
2. SI unit of electric current is ‘ampere’ and it is denoted as A.
Question 4.
Define super conductors.
Answer:
At very low temperature, around 30 K (-243.2° C), some conductors conduct electric current without any loss. These conductors are known as ‘SUPER CONDUCTORS’.
Question 5.
Define amount of substance. Mention its SI unit and symbol.
Answer:
- Amount of substance is a measure of the number of entities (particles) present in a substance.
- The SI unit of amount of substance is mole and it is denoted as ‘mol’.
Question 6.
What is luminous intensity? Mention its SI unit and symbol.
Answer:
- The measure of the power of the emitted light, by a light source in a particular direction, per unit solid angle is called as luminous intensity.
- The SI unit of luminous intensity is candela and is denoted as ‘cd’.
![]()
Question 7.
What are the rules for rounding off a number?
Answer:
Rules for rounding off:
- Decide which is the last digit to keep.
- Leave it the same, if the next digit is less than 5.
- Increase it by one, if the next digit is 5 or greater than 5.
Question 8.
Define one light year.
Answer:
One light year is defined as the distance travelled by light in vacuum during the period of one year. 1 light year = 9.46 x 1015m
VIII. Long Answers
Question 1.
Write a note on accuracy and precision.
Answer:
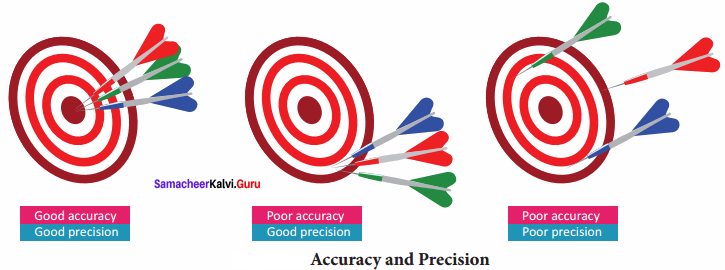
Accuracy in Measurements:
1. Measurement is the base of all experiments in science and technology. The value of every measurement contains some uncertainty. These uncertainties are called as ‘Errors’.
2. The difference between the real value and the observed value is called an error.
- Accuracy : Accuracy is the closeness of a measured value to the actual value or true value.
- Precision : Precision is the closeness of two or more measurements to each other.
Question 2.
Explain the Greenwich mean time.
Answer:
- Greenwich Mean Time (GMT) is the mean solar time at the Royal Observatory, located at Greenwich in London.
- It is measured at the longitude of zero degree.
- The Earth is divided into 24 zones, each of a width of 15 degree longitude.
- These regions are called as ‘Time Zones’. Time difference between two adjacent time zones is 1 hour.
Question 3.
Write a note on approximation.
Answer:
- Approximation is the process of finding a number, which is acceptably close to the exact value of the measurement of a physical quantity.
- It is an estimation of a number obtained by rounding off a number to its nearest place value.
- When the data are inadequate, physicists are in need of an approximation to find the solution for problems.
- Approximations are usually based on certain assumptions having a scientific background and they can be modified whenever accuracy is needed.
IX. Complete the given table
 Answer:
Answer:
(i) 0° C
(ii) 100
(iii) 212° F
(iv) 373 K
(v) 100
X. Problems for practice
Question 1.
Convert 36° C into kelvin.
Solution:
K = C + 273
= 36 + 273
= 309 K
Question 2.
Convert 100 K into Celsius.
Solution:
C = K – 273
C = 100 – 273
= -173° C
![]()
Question 3.
When 5 coulomb of charge, flows through a circuit for 20 seconds. Calculate the current?
Given: Charge Q = 5 C
Time t = 20 s
Solution:
I = \(\frac { Q }{ t }\) = \(\frac { 5}{ 20 }\) = 0.25 A
I = 0.25 A
Question 4.
Convert 90° C into radian.
Given: i = \(\frac { π }{ 180° }\)
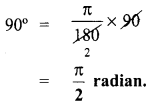
Question 5.
Round off the number 5.323 to two decimal places.
Answer:
Step : 1 Identify the last digit to be kept. 2 is the last digit to be kept.
Step : 2 The following digit, (i.e.) 3 is less than 5. SI retain 2 as 2.
∴ The answer is 5.32.