Students can Download Maths Chapter 2 Life Mathematics Ex 2.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 3 Chapter 2 Life Mathematics Ex 2.2
Miscellaneous and Practice Problems
Question 1.
5 boys or 3 girls can do a science project in 40 days. How long will it take for 15 boys and 6 girls to do the same project?
Solution:
Let B and G denote Boys and Girls respectively.
Given 5B = 3G ⇒ 1B = \(\frac{3}{5}\)G
now 15B + 6G = 15 × \(\frac{3}{5}\) G + 6G = 9G + 6G = 15G
If 3 girls can do the project in 40 days then 15 girls can do it in
3G × 40 ÷ 15G = 3G × 40 × \(\frac{1}{15G}\) = \(\frac{40}{5}\)
= 8 days.
∴ 15 boys and 6 girls can complete the project in 8 days.
![]()
Question 2.
If 32 men working 12 hours a day can do a work in 15 days, how many men working 10 hours a day can do double that work in 24 days?
Solution:
Let the required number of men be x.

Let P1= 32, H1 = 12, D1 = 12, W1 = 1
P2 = x, H2 = 10, D2 = 24, W2 = 1
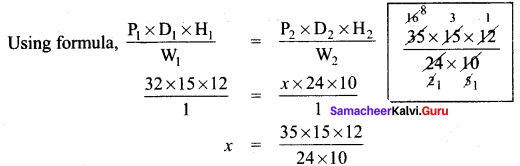
x = 24 persons
To complete the same work 24 men needed.
To complete double the work 24 × 2 = 48 men are required.
Question 3.
Amutha can weave a saree in 18 days. Anjali is twice as good a weaver as Amutha. If both of them weave together, in how many days can they complete weaving the saree?
Solution:
Amutha can weave a saree in 18 days. Anjali is twice as good as Amutha.
ie. If Amutha weave for 2 days, Anjali do the same work in 1 day.
If Anjali weave the saree she will take
\(\frac{18}{2}\) = 9 days
Hence time taken by them together = \(\frac{ab}{a + b}\) days = \(\frac{18 × 9}{18 + 9}\) = \(\frac{18 × 9}{27}\) = 6 days
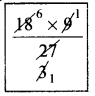
In 6 days they complete weaving the saree.
Question 4.
A, B and C can complete a work in 5 days. If A and C can complete the same work in 7½ days and A alone in 15 days then, in how many days can B and G finish the work?
Solution:
A + B + C complete the work in 5 days.
∴ (A + B + C)’s 1 day work = \(\frac{1}{5}\)
(A + C) complete the work in 7 \(\frac{1}{2}\) days = \(\frac{15}{2}\) days
∴ (A + C)’s 1 day work = \(\frac{1}{\frac{15}{2}}\) = \(\frac{2}{15}\)
∴ B’s 1 day work = (A + B + C)’s 1 day work – (A + C)’s 1 day work.
\(\frac{1}{5}\) – \(\frac{2}{15}\) = \(\frac{3}{15}\) – \(\frac{2}{15}\)
C’s 1 day work = (A + C)’s 1 day work – A’s 1 day work
= \(\frac{2}{5}\) – \(\frac{1}{15}\) = \(\frac{1}{15}\)
Now (A + C)’s 1 day work = B’s 1 day work + C’s 1 day work
= \(\frac{1}{15}\) + \(\frac{1}{15}\) = \(\frac{2}{15}\)
∴ (B + C) can complete the work in \(\frac{1}{\frac{2}{15}}\) days. = \(\frac{15}{2}\) days = 7\(\frac{1}{2}\) days
∴B and C finish the work in 7\(\frac{1}{2}\) days.
Question 5.
P and Q can do a piece of work in 12 days and 15 days respectively. P started the work alone and then, after 3 days Q joined him till the work was completed. How long did the work last?
Solution:
p can do a piece of work in 12 days.
∴ p’s 1 day work = \(\frac{1}{12}\)
p’s 1 day work = 3 × \(\frac{1}{12}\) = \(\frac{3}{12}\)
Q can do a piece of work in 15 days.
∴ Q’s 1 day work = \(\frac{1}{15}\)
Remaining work after 3 days = 1 – \(\frac{3}{12}\) = \(\frac{9}{12}\)
(P + Q)’s 1 day work = \(\frac{1}{12}\) + \(\frac{1}{15}\) = \(\frac{5}{60}\) + \(\frac{4}{60}\) = \(\frac{9}{60}\)
Number of days required to finish the remaining work
= \(\frac{Remaining work}{(P + Q)’s 1 day work}\) = \(\frac{\frac{9}{12}}{\frac{9}{60}}\) = \(\frac{9}{12}\) × \(\frac{60}{9}\) = 5
Remaining work lasts for 5 days. Total work lasts for 3 + 5 = 8 days.
![]()
Challenging Problems
Question 6.
A camp had provisions for 490 soldiers for 65 days. After 15 days, more soldiers arrived and the remaining provisions lasted for 35 days. How many soldiers joined the camp?
Solution:

Now as the soldiers increases food last for less days.
∴ It is inverse proportion.
The proportion is (490 + x): 490 : : 50 : 35
Product of the extremes = Product of the means
(490 + x) × 35 = 490 × 50
(490 + x) = \(\frac{490 × 50}{35}\)
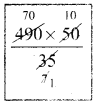
x = 700 – 490
x = 210
∴ 210 soldiers joined the camp.
Question 7.
A small – scale company undertakes an agreement to produce 540 motor pumps in 150 days and employs 40 men for the work. After 75 days, the company could make only 180 motor pumps. How many more men should the company employ so that the work is completed on time as per the agreement?
Solution:
Let the number of men to be appointed more be x.

To produce more pumps more men required
∴ It is direct variation.
∴ The multiplying factor is \(\frac{360}{180}\)
More days means less employees needed.
∴ It is Indirect proportion.
∴ The multiplying factor is \(\frac{75}{75}\)
Now 40 + x = 40 × \(\frac{360}{180}\) × \(\frac{75}{75}\)
40 + x = 80
x = 80 – 40
x = 40
40 more man should be employed to complete the work on time as per the agreement.
Question 8.
A can do a work in 45 days. He works at it for 15 days and then, B alone finishes the remaining work in 24 days. Find the time taken to complete 80% of the work if they work together.
Solution:
A can do a work in 45 days.
A’s 1 day work = \(\frac{1}{45}\)
∴ A’s 15 days work = 15 × \(\frac{1}{45}\) = \(\frac{1}{3}\)
Remaining work = 1 – \(\frac{1}{3}\) = \(\frac{2}{3}\)
B alone completes the remaining \(\frac{2}{3}\) work in 24 days
∴ B completes the whole work in \(\frac{24}{\frac{2}{3}}\) days = 24 × \(\frac{3}{2}\) = 36 days.
∴ B’s 1 day’s work = \(\frac{1}{36}\)
∴ (A + B)’s together complete the work in \(\frac{ab}{a + b}\) days = \(\frac{45 × 36}{45 + 36}\) = \(\frac{45 × 36}{81}\)
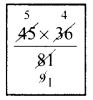
Whole wok will be completed by (A + B) in = 20 days.
∴ 80% of the work will be completed in \(\frac{80 × 20}{100}\) = 16 days.
Question 9.
P alone can do \(\frac{1}{2}\) of a work in 6 days and Q alone can do \(\frac{2}{3}\) of the same work in 4 days. In how many days working together, will they finish \(\frac{3}{4}\) of the work?
Solution:
\(\frac{1}{2}\) of the work is done by P in 6 days
∴ Full work is done by P in \(\frac{6}{\frac{1}{2}}\) = 6 × 2 = 12 days
\(\frac{2}{3}\) of work done by Q in 4 days.
∴ Full work done by Q in \(\frac{4}{\frac{2}{3}}\) = 4 × \(\frac{3}{2}\) = 6 days
(P + Q) will finish the whole work in \(\frac{ab}{a + b}\) days = \(\frac{12 × 6}{12 + 6}\) = \(\frac{12 × 6}{18}\) = 4 days
(P + Q) will finish \(\frac{3}{4}\) of the work in 4 × \(\frac{3}{4}\) = 3 days.
![]()
Question 10.
X alone can do a piece of work in 6 days and Y alone in 8 days. X and Y undertook the work for Rs 4800. With the help of Z, they completed the work in 3 days. How much is Z’s share?
Solution:
X can do the work in 6 days.
X’s 1 day work = \(\frac{1}{6}\)
X’s share for 1 day = \(\frac{1}{6}\) × 48000 = Rs 800
X’s share for 3 days = 3 × 800 = 2400
Y can complete the work in 8 days.
Y’s 1 day work = \(\frac{1}{8}\)
Y’s 1 day share = \(\frac{1}{8}\) × 4800 = 600
Y’s 3 days share = 600 × 3 = 1800
(X + Y)’s 3 days share = 2400 + 1800 = 4200
Remaining money is Z’s share
∴ Z’s share = 4800 – 4200 = 600