Students can Download Maths Chapter 2 Life Mathematics Ex 2.1 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 3 Chapter 2 Life Mathematics Ex 2.1
Question 1.
Fill in the blanks:
(i) A can finish a job in 3 days whereas B finishes it in 6 days. The time taken to complete the job together is………..days.
(ii) If 5 persons can do 5 jobs in 5 days, then 50 persons can do 50 jobs in………..days.
(iii) A can do a work in 24 days. A and B together can finish the work in 6 days. Then B alone can finish the work in…………days.
(iv) A alone can do a piece of work in 35 days. If B is 40% more efficient than A, then B will finish the work in………..days.
(v) A alone can do a work in 10 days and B alone in 15 days. They undertook the work for Rs 200000. The amount that A will get is………
Solution:
(i) 2 days
(ii) 5
(iii) 8
(iv) 25
(v) Rs 1,20,000
![]()
Question 2.
210 men working 12 hours a day can finish a job in 18 days. How many men are required to finish the job in 20 days working 14 hours a day?
Solution:
Let the required number of men be x.

More working hours ⇒ less men required.
∴ It is inverse proportion.
∴ Multiplying factor is \(\frac{12}{14}\)
Also more number of days ⇒ less men
∴ It is an inverse proportion.
∴ Multiplying factor is \(\frac{18}{20}\)
∴ x = 210 × \(\frac{12}{14}\) × \(\frac{18}{20}\)= 162 men
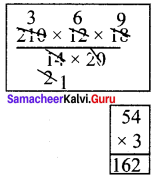
162 men are required.
Question 3.
A cement factory makes 7000 cement bags in 12 days with the help of 36 machines. How many bags can be made in 18 days using 24 machines?
Solution:
Let the required number of cement bags be x.

Number of days more ⇒ More cement bags.
∴ It is direct variation.
∴ The multiplying factor = \(\frac{18}{12}\)
Number of machines more ⇒ More cement bags.
∴ It is direct variation.
∴ The multiplying factor = \(\frac{24}{36}\)
∴ x = 7000 × \(\frac{18}{12}\) × \(\frac{24}{36}\)
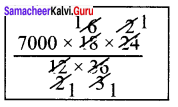
x = 7000 cement bags
7000 cement bags can be made.
Question 4.
A soap factory produces 9600 soaps in 6 days working 15 hours a day. In how many days will it produce 14400 soaps working 3 hours more a day?
Solution:
Let the required number of days be x.
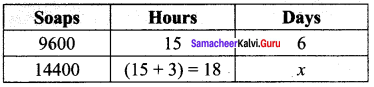
To produce more soaps more days required.
∴ It is direct proportion.
∴ Multiplying factor = \(\frac{14400}{9600}\)
If more hours spend, less days required.
∴ It is indirect proportion.
∴ Multiplying factor = \(\frac{15}{18}\)
∴ x = 6 × \(\frac{14400}{9600}\) × \(\frac{15}{18}\)
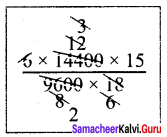
x = \(\frac{15}{2}\)
\(\frac{15}{2}\) days will be needed.
Question 5.
If 6 container lorries transport 135 tonnes of goods in 5 days, how many more lorries are required to transport 180 tonnes of goods in 4 days?
Solution:
Let the number of lorries required more = x.
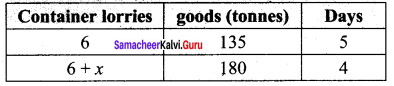
As the goods are more ⇒ More lorries are needed to transport.
∴ It is direct proportion.
∴ Multiplying factor = \(\frac{180}{135}\)
Again if more days ⇒ less number of lorries enough.
∴ It is direct proportion.
∴ Multiplying factor = \(\frac{5}{4}\)
∴ 6 + x = 6 × \(\frac{180}{135}\) × \(\frac{5}{4}\)
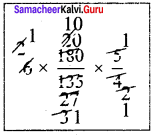
6 + x = 10
x = 10 – 6
x = 4
∴ 4 more lorries are required.
![]()
Question 6.
A can do a piece of work in 12 hours, B and C can do it 3 hours whereas A and C can do it in 6 hours. How long will B alone take to do the same work?
Solution:
Time taken by A to complete the work =12 hrs.
∴ A’s 1 hr work = \(\frac{1}{12}\)…………(1)
(B + C) complete the work in 3 hrs.
∴ (B + C)’s 1 hour work = \(\frac{1}{3}\)…………(2)
(1) + (2) ⇒
∴ (A + B + C)’s 1 hour work = \(\frac{1}{12}\) + \(\frac{1}{3}\) = \(\frac{1+4}{12}\) = \(\frac{5}{12}\)
Now (A + C) complete the work in 6 hrs.
∴(A + C)’s 1 hour work = \(\frac{1}{6}\)
∴ B’s 1 hour work = (A + B + C)’s 1 hour work – (A + C)’s 1 hour work
= \(\frac{5}{12}\) – \(\frac{1}{6}\) = \(\frac{5-2}{12}\) = \(\frac{3}{12}\) = \(\frac{1}{4}\)
∴ B alone take 4 days to complete the work.
Question 7.
A and B can do a piece of work in 12 days, while B and C can do it in 15 days whereas A and C can do it in 20 days. How long would each take to do the same work?
Solution:
(A + B) complete the work in 12 days.
∴ (A + B)’s 1 day work = \(\frac{1}{12}\)……….(1)
(B + C) complete the work in 15 days
∴ (B + C)’s 1 day work = \(\frac{1}{15}\)……….(2)
(A + C) complete the work in 20 days
∴ (A + C)’s 1 day work = \(\frac{1}{20}\)……….(3)
Now (1) + (2) + (3) ⇒
[(A + B) + (B + C) + (A + C)]’s 1 day work = \(\frac{1}{12}\) + \(\frac{1}{15}\) + \(\frac{1}{20}\)
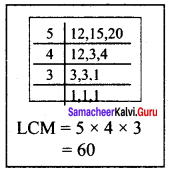
(2A + 2B + 2C)’s 1 day work = \(\frac{5}{60}\) + \(\frac{4}{60}\) + \(\frac{3}{60}\)
2(A + B + C)’s 1 day work = \(\frac{5+4+3}{60}\)
(A + B + C)’s 1 day work = \(\frac{12}{60×2}\)
(A + B + C)’s 1 day work = \(\frac{1}{10}\)
Now A’s 1 day’s work = (A + B + C)’s 1 day work – (B + C)’s 1 day work
\(\frac{1}{10}\) – \(\frac{1}{15}\) = \(\frac{3}{30}\) – \(\frac{2}{30}\) = \(\frac{1}{30}\)
∴ A takes 30 days to complete the work.
B’s 1 day work = (A + B + C)’s 1 day’s work – (A + C)’s 1 day’s work
= \(\frac{1}{10}\) – \(\frac{1}{20}\) = \(\frac{6}{60}\) – \(\frac{3}{60}\)
\(\frac{6-3}{60}\) = \(\frac{3}{60}\) = \(\frac{1}{20}\)
B takes 20 days to complete the work.
C’s 1 day work = (A + B + C)’s 1 day work – (A + B)’s 1 day work
\(\frac{1}{10}\) – \(\frac{1}{12}\) = \(\frac{6}{60}\) – \(\frac{5}{60}\) = \(\frac{6-5}{60}\) = \(\frac{1}{60}\)
∴ C takes 60 days to complete the work.
![]()
Question 8.
Carpenter A takes 15 minutes to fit the parts of a chair while Carpenter B takes 3 more minutes than A to do the same work. Working together, how long will it take for them to fit the parts for 22 chairs?
Solution:
Time taken by A to fit a chair = 15 minutes
Time taken by B = 3 minutes more than A
= 15 + 3 = 18 minutes
∴ A’s 1 minute work = \(\frac{1}{15}\)
B’s 1 minute work = \(\frac{1}{18}\)
(A + B)’s 1 minutes work = \(\frac{1}{15}\) + \(\frac{1}{18}\)
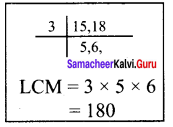
\(\frac{12}{180}\) + \(\frac{22}{180}\) = \(\frac{22}{180}\) = \(\frac{11}{90}\)
∴ Time taken by (A + B) to fit a chair
= \(\frac{1}{\frac{11}{90}}\) = \(\frac{90}{11}\) minutes
∴ Time taken by (A + B) to fit 22 chairs
= \(\frac{90}{11}\) × 22 = 180 minutes
= \(\frac{180}{60}\) = 3 hours
Question 9.
A man takes 10 days to finish a job where as a woman takes 6 days to finish the same job. Together they worked for 3 days and then the woman left. In how many days will the man complete the remaining job?
Solution:
Man can finish the work in 10 days and women can finish the same work in 6 days.
∴ Man’s 1 day work = \(\frac{1}{10}\)
Woman’s 1 day work = \(\frac{1}{6}\)
(Man + Woman)s 1 day work = \(\frac{1}{10}\) + \(\frac{1}{6}\) = \(\frac{6}{60}\) + \(\frac{10}{60}\) = \(\frac{16}{60}\)
(Man + Woman)s 3 days work

In 3 days \(\frac{4}{5}\) th of the whole work is completed.
Remaining work = 1 – \(\frac{4}{5}\) = \(\frac{5}{5}\) – \(\frac{4}{5}\) = \(\frac{1}{5}\)
Complete work is done by the man by 10 days
∴ \(\frac{1}{5}\) of the work is done by man in \(\frac{1}{5}\) × 10 = 2 days.
![]()
Question 10.
A is thrice as fast as B. If B can do a piece of work in 24 days then, find the number of days they will take to complete the work together.
Solution:
If B does the work in 3 days, A will do it in 1 day.
B complete the work in 24 days.
∴ A complete the same work in \(\frac{24}{3}\) = 8 days.
∴ (A + B) complete the work in \(\frac{ab}{a+b}\) days = \(\frac{24×8}{24+8}\) days = \(\frac{24×8}{32}\)days = 6 days
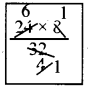
They together complete the work in 6 days.