Students can Download Maths Chapter 3 Algebra Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 3 Algebra Additional Questions
Additional Questions and Answers
Exercise 3.1
Question 1.
Simplify the following and write the answer in Exponential form.
(i) 32 × 34 × 38
(ii) 615 ÷ 610
(iii) a3 × a2
(iv) 7x × 72
(v) (52)3 ÷ 53
Solution:
(i) 32 × 34 × 32 = 32+4+8 = 314 [∵ am × an = am+n]
So 32 × 34 × 32 = 314
(ii) 615 ÷ 610 = 615-10 = 65 [∵ am × an = am-n]
(iii) a3 × a2 = a3+2 = a5
(iv) 7x × 72 = 7x+2
(v) (52)3 ÷ 53 = 52×3 ÷ 53 = 56 ÷ 53 [∵ (am)n = am×n]
![]()
Question 2.
Express the following as a product of factors only in exponential form
(i) 108 × 192
(ii) 270
(iii) 729 × 64
(iv) 768
Solution:
(i) 108 × 192
108 = 2 × 2 × 3 × 3 × 3
192 = 2 × 2 × 2 × 2 × 2 × 2 × 3
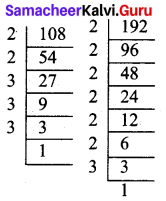
∴ 108 × 192 = (2 × 2 × 3 × 3 × 3) ×
(2 × 2 × 2 × 2 × 2 × 2 × 3)
= 28 × 34
Thus 108 × 192 = 28 × 34
(ii) 270
We have 270 = 2 × 3 × 3 × 3 × 5

= 21 × 33 × 51
= 2 × 33 × 5
So 270 = 2 × 33 × 5
(iii) 729 × 64
729 = 3 × 3 × 3 × 3 × 3 × 3
64 = 2 × 2 × 2 × 2 × 2 × 2
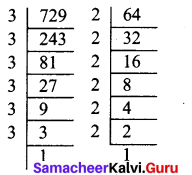
729 × 64 = (3 × 3 × 3 × 3 × 3 × 3)
× (2 × 2 × 2 × 2 × 2 × 2)
= 36 × 26
∴ 729 × 64 = 36 × 26
(iv) 768
We have 768 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3

= 28 × 31
= 28 × 3
Thus 768 = 28 × 3
![]()
Question 3.
Identify the greater number, wherever possible in each of the following.
(i) 53 or 35
(ii) 28 or 82
(iii) 1002 or 21000
(iv) 210 or 102
Solution:
(i) 53 or 35 53 = 5 × 5 × 5 = 125
35 = 3 × 3 × 3 × 3 × 3 = 243
243 > 125 ∴ 35 > 53
(ii) 28 or 82 28 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 256
82 = 8 × 8 = 64
256 > 64 ∴ 28 > 82
(iii) 1002 or 21000
We have 1002 = 100 × 100 = 10000
2100 = (210)10 = (2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2)10
= (1024)10 = [(1024)2]5
= (1024 × 1024)5 = (1048576)5
Since 1048576 > 10000
(1048576)5 > 10000
i.e., (1048576) > 1002
(210)10 > 1002
2100 > 1002
(iv) 210 or 102
We have 210 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 1024
102 = 10 × 10 = 100
Since1 1024 > 100
210 > 102
![]()
Exercise 3.2
Question 1.
Find the unit digit of the following exponential numbers.
(i) 255223
(ii) 81111000
(iii) 4866431
Solution:
(i) 255223
Unit digit of base 255 is 5 and power is 223.
Thus the unit digit of 255223 is 5.
(ii) 81111000
Unit digit of base 8111 is 1 and power is 1000.
Thus the unit digit of 81111000 is 1.
(iii) 4866431
Unit digit of base 4866 is 6 and power is 431.
Thus the unit digit of 4866431 is 6.
Question 2.
Find the unit digit of the numbers
(i) 1844671
(ii) 1564100
Solution:
(i) 1844671
Unit digit of base 1844 is 4 and the power is 671 (odd power)
Therefore unit digit of 1844671 is 4
(ii) 1564100
Unit digit of base 1564 is 4 and the power is 100 (even power)
Therefore unit digit of 1564100 is 6.
Question 3.
Find the unit digit of the numbers
(i) 999222
(ii) 1549777
Solution:
(i) 999222
Unit digit of base 999 is 9 and the power is 222 (even power).
Therefore, unit digit of 999222 is 1.
(ii) 1549777
Unit digit of base 1549 is 9 and the power is 777 (odd power).
Therefore, unit digit of 1549777 is 9.
![]()
Question 4.
Find the unit digit of 1549101 + 654120
Solution:
1549101 + 654120
In 1549101, the unit digit of base 1549 is 9 and power is 101 (odd power).
Therefore, unit digit of the 1549101 is 9.
In 654120, the unit digit of base 6541 is 1 and power is 20 (even power).
Therefore, unit digit of the 654120 is 1.
∴ Unit digit of 1549101 + 654120 is 9 + 1 = 10
∴ Unit digit of 1549101 + 654120 is 0.
Exercise 3.3
Question 1.
Find the degree of the following polynomials.
(i) x5 – x4 + 3
(ii) 2 – y5 – y3 + 2y8
(iii) 2
(iv) 5x3 + 4x2 + 7x
(v) 4xy + 7x2y + 3xy3
Solution:
(i) x5 – x4 + 3
The terms of the given expression are x5, -x4, 3.
Degree of each of the terms : 5, 4, 0
Term with highest degree: x5
Therefore degree of the expression in 5.
(ii) 2 – y5 – y3 + 2y8
The terms of the given expression are 2, -y5 ,-y3, 2y8.
Degree of each of the terms : 0, 2, 3, 8.
Term with highest degree: 2y8
Therefore degree of the expression in 8.
(iii) 2
Degree of the constant term is 0.
∴ Degree of 2 is 0.
(iv) 5x3+ 4x2 + 7x
The terms of the given expression are 5x3, 4x2, 7x
Degree of each of the terms : 3, 2, 1
Term with highest degree: 5x3
Therefore degree of the expression in 3.
(v) 4xy + 7x2y + 3xy3
The terms of the given expression are 4xy , 7x2y, 3xy3
Degree of each of the terms : 2, 3, 4
Term with highest degree: 3xy3
Therefore degree of the expression in 4.
![]()
Question 2.
State whether a given pair of terms in like or unlike terms.
(i) 1,100
(ii) -7x,\(\frac { 5 }{ 2 } \)x
(iii) 4m2p, 4mp2
(iv) 12xz, 12x2z2
Solution:
(i) 1, 100 is a pair of like terms. [∵ 1 = x0 and 100 = 100 x0]
(ii) -7x, \(\frac { 5 }{ 2 } \)x is a pair of like terms.
(iii) 4m2p, Amp is a pair of unlike terms.
(iv) 12xz, 12x2z2 is a pair of unlike terms.
Question 3.
Subtract 5a2 – 7ab + 5b2 from 3ab – 2a2 – 2b2 and find the degree of the expression
Solution:
(i) We have (3ab – 2a2 – 2b2) – (5a2 – 7ab + 5b2)
= 3ab – 2a2 – 2b2 – 5a2 + 7ab – 5b2
= (3ab + 7ab) + (- 2 – 5)a2 + (- 2 – 5)b2
= 10 ab + (-7)a2 + (-7)b2
= 10ab – 7a2 – 7b2
Degree of the expression is 2.
Question 4.
Add x2 – y2 -1,y2 – 1 – x2, 1 – x2 – y2 and find the degree of the expression.
Solution:
We have (x2 – y2 – 1) + (y2 – 1 – x2) + (1 – x2 – y2)
= x2 – y2 – 1 + y2 – 1 – x2 + 1 – x2 – y2
= (x2 – x2 – x2) + (-y2 + y2 – y2) + (- 1 – 1 + 1)
= (1 – 1 – 1)x2 + (- 1 + 1 – 1)y2 + ( – 2 + 1)
= (- 1) x2 + (- 1)y2 + (-1) = – x2 – y2 – 1
Degree of the expression is 2.
![]()
Question 5.
Find the degree of the terms
(i) x2
(ii) 4xyz
(iii) \(\frac{7 x^{2} y^{4}}{x y}\)
(iv) \(\frac{x^{2} \times y^{2}}{x \times y^{2}}\)
Solution:
We have
(i) x2
The exponent in x2 is 2. ∴ Degree of the term is 2.
(ii) 4xyz
In 4xyz the sum of the powers of x, y and z as 3.
(iii) \(\frac{7 x^{2} y^{4}}{x y}\)
We have \(\frac{7 x^{2} y^{4}}{x y}\) = 7x2-1 y4-1 = 7x1y3 [Since \(\frac{a^{m}}{a^{n}}\) = am-n]
In 7 x1 y3 the sum of the poweres of x and y is 4(1 + 3 = 4)
Thus degree of the expression is 4.
(iv) \(\frac{x^{2} \times y^{2}}{x \times y^{2}}\)
We have \(\frac{x^{2} \times y^{2}}{x \times y^{2}}\) = x2-1 y2-2 = x1 y0 = x1 [∵ y0 = 1]
The exponent of the expression is 1.