Students can Download Maths Chapter 6 Information Processing Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 3 Chapter 6 Information Processing Additional Questions
Exercise 6.1
Question 1.
Draw a flowchart to calculate simple interest for your bank deposit.
Solution:
Flow Chart:
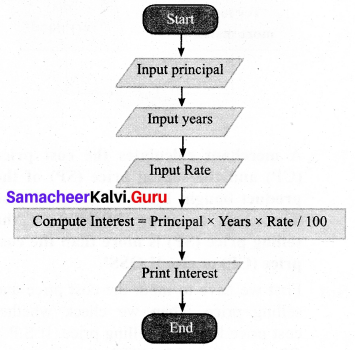
Algorithm:
(i) Read principal
(ii) Read years
(iii) Read rate of interest per year
(iv) Calculate the interest with formula Interest = Principal × Years × Rate/100
(v) Print Interest
![]()
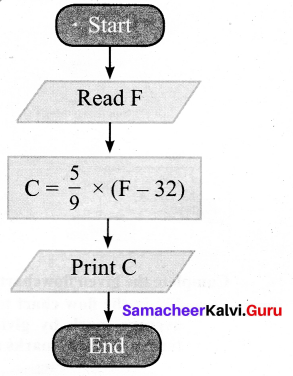
Question 2.
Draw a flowchart to convert the given Fahrenheit temperature to Celsius. Formula is C = \(\frac { 5 }{ 9 } \) × (F – 32)
Solution:
Algorithm:
(i) Read temperature in Fahrenheit
(ii) Calculate temperature in Celsius using formula C = \(\frac { 5 }{ 9 } \) × (F – 32)
(iii) Print C