Students can Download Maths Chapter 3 Algebra Ex 3.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 3 Chapter 3 Algebra Ex 3.2
Question 1.
Given that x > y. Fill in the blanks with suitable inequality signs.
(i) y [ ] x
(ii) x+ 6 [ ] y + 6
(iii) x2 [ ] xy
(iv) -xy [ ] – y2
(v) x – y [ ] 0
Answer:
(i) y [<] x
(ii) x+ 6 [>] y + 6
(iii) x2 [>] xy
(iv) -xy [<] – y2
(v) x – y [>] 0
![]()
Question 2.
Say True or False.
(i) Linear inequation has almost one solution.
Answer:
False
(ii) When x is an integer, the solution set for x < 0 are -1, -2,..
Answer:
False
(iii) An inequation, -3 < x < -1, where x is an integer, cannot be represented in the number line.
Answer:
True
(iv) x < -y can be rewritten as – y < x
Ans :
False
Question 3.
Solve the following inequations.
(i) x < 7, where x is a natural number.
(ii) x – 6 < 1, where x is a natural number.
(iii) 2a + 3 < 13, where a is a whole number.
(iv) 6x – 7 > 35, where x is an integer.
(v) 4x – 9 > -33, where x is a negative integer.
Solution:
(i) x < 7, where x is a natural number.
Since the solution belongs to the set of natural numbers, that are less than or equal to 7, we take the values of x as 1,2, 3, 4, 5, 6 and 7.
(ii) x – 6 < 1, where x is a natural number.
x – 6 < 1 Adding 6 on the both the sides x – 6 + 6 < 1 + 6
x < 7
Since the solutions belongs to the set of natural numbers that are less than 7, we take the values of x as 1,2, 3, 4, 5 and 6
(iii) 2a + 3 < 13, where a is a whole number.
2a + 3 < 13
Subtracting 3 from both the sides 2a + 3 – 3 < 13 – 3
2a < 10
Dividing both the side by 2. \(\frac { 2a }{ 2 } \) < \(\frac { 10 }{ 2 } \)
a < 5
Since the solutions belongs to the set of whole numbers that are less than or equal to 5 we take the values of a as 0, 1, 2, 3, 4 and 5
![]()
(iv) 6x – 7 > 35, where x is an integer.
6x – 7 > 35 Adding 7 on both the sides
6x – 7 + 7 > 35 + 7
6x > 42
Dividing both the sides by 6 we get \(\frac { 6x }{ 6 } \) > \(\frac { 42 }{ 6 } \)
x > 7
Since the solution belongs to the set of integers that are greater than or equal to 7, we take the values of x as 7, 8, 9, 10…
(v) 4x – 9 > -33, where x is a negative integer.
4x – 9 > – 33 + 9 Adding 9 both the sides
4x – 9 + 9 > -33 + 9
4x > – 24
Dividing both the sides by 4
\(\frac { 4x }{ 4 } \) > \(\frac { -24 }{ 4 } \)
x > -6
Since the solution belongs to a negative integer that are greater than -6, we take values of u as -5, -4, -3, -2 and -1
![]()
Question 4.
Solve the following inequations and represent the solution on the number line:
(i) k > -5, k is an integer.
(ii) -7 < y, y is a negative integer.
(iii) -4 < x < 8, x is a natural number.
(iv) 3m – 5 < 2m + 1, m is an integer.
Solution:
(i) k > -5, k is an integer.
Since the solution belongs to the set of integers, the solution is -4, -3, -2, -1, 0,… It’s graph on number line is shown below.
![]()
(ii) -7 < y, y is a negative integer.
-7 < y
Since the solution set belongs to the set of negative integers, the solution is
-7, -6, -5, -4, -3, -2, -1.
Its graph on the number line is shown below
![]()
(iii) -4 < x < 8, x is a natural number.
-4 < x < 8
Since the solution belongs to the set of natural numbers, the solution is
1, 2, 3, 4, 5, 6, 7 and 8.
Its graph on number line is shown below
![]()
(iv) 3m – 5 < 2m + 1, m is an integer.
3m – 5 < 2m + 1
Subtracting 1 on both the sides
3m – 5 – 1 < 2m + 1 + 1
3m – 6 < 2m
Subtracting 2m on both the sides 3m- 6 – 2m < 2m -2m
m – 6 < 0
Adding 6 on both the sides m – 6 + 6 < 0 + 6
m < 6
Since the solution belongs to the set of integers, the solution is
6, 5, 4, 3, 2, 1, 0,-1,…
Its graph on number line is shown below
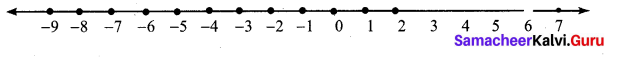
![]()
Question 5.
An artist can spend any amount between ₹ 80 to ₹ 200 on brushes. If cost of each brush is ₹ 5 and there are 6 brushes in each packet, then how many packets of brush can the artist buy?
Solution:
Given the artist can spend any amount between ₹ 80 to ₹ 200
Let the number of packets of brush he can buy be x
Given cost of 1 brush = ₹ 5
Cost of 1 packet brush (6 brushes) = ₹ 5 × 6 = ₹ 30
∴ Cost of x packets of brushes = 30 x
∴ The inequation becomes 80 < 30x < 200
Dividing throughout by 30 we get \(\frac { 80 }{ 30 } \) < \(\frac { 30x }{ 30 } \) < \(\frac { 200 }{ 30 } \)
\(\frac { 8 }{ 3 } \) < x < \(\frac { 20 }{ 3 } \) ;
2 \(\frac { 2 }{ 3 } \) < x < 6 \(\frac { 2 }{ 3 } \)
brush packets cannot get in fractions.
∴ The artist can buy 3 < x < 6 packets of brushes,
or x = 3, 4, 5 and 6 packets of brushes.
![]()
Objective Type Questions
Question 1.
The solutions set of the inequation 3 < p < 6 are (where p is a natural number)
(i) 4,5 and 6
(ii) 3,4 and 5
(iii) 4 and 5
(iv) 3,4,5 and 6
Answer:
(iv) 3,4,5 and 6
Question 2.
The solution of the inequation 5x + 5 < 15 are (where x is a natural number)
(i) 1 and 2
(ii) 0,1 and 2
(iii) 2, 1,0, -1,-2
(iv) 1, 2, 3..
Answer:
(i) 1 and 2
Hint: 5x + 5 < 15
5x < 15 – 5 = 10
x < \(\frac { 10 }{ 5 } \) = 2
![]()
Question 3.
The cost of one pen is ₹ 8 and it is available in a sealed pack of 10 pens. If Swetha has only ₹ 500, how many packs of pens can she buy at the maximum?
(i) 10
(ii) 5
(iii) 6
(iv) 8
Answer:
(iii) 6
Hint:
Price of 1 pen = ₹ 8
Price of 1 pack = 10 × 8 = 80
Number of packs Swetha can buy = x
80x < 500
8x < 50
x < \(\frac { 50 }{ 8 } \) = 6.25
x is a natural number x = 1, 2, 3, 4, 5, 6
![]()
Question 4.
The inequation that is represented on the number line as shown below is _______.
![]()
(i) -4 < x < 0
(ii) -4 < x < 0
(iii) -4 < x < 0
(iv) -4 < x < 0
(v) -4 < x < 2
Answer:
(v) -4 < x < 2