You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
![]()
Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 4 Geometry Ex 4.4
Miscellaneous Practice Problems
Question 1.
Find the type of lines marked in thick lines (Parallel, intersecting or perpendicular)
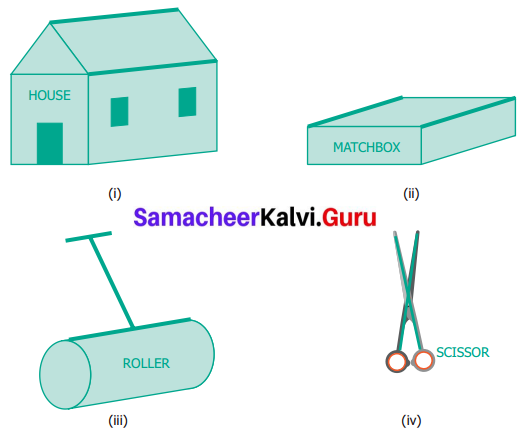
Solution:
(i) Parallel lines
(ii) Parallel lines
(iii) Parallel lines and Perpendicular lines
(iv) Intersecting lines
Question 2.
Find the parallel and intersecting line segments in the picture given below.
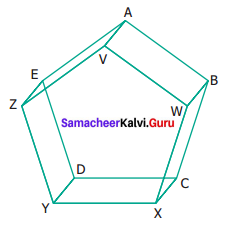
Solution:
Parallel lines:
\(\overline { YX }\) and \(\overline { DC }\)
\(\overline { YD }\) and \(\overline { ZE }\)
\(\overline { XC }\) and \(\overline { YD }\)
\(\overline { YZ }\) and \(\overline { DE }\)
\(\overline { XW }\) and \(\overline { BC }\)
\(\overline { XC }\) and \(\overline { WB }\)
\(\overline { WV }\) and \(\overline { BA }\)
\(\overline { ZV }\) and \(\overline { EA }\)
\(\overline { VA }\) and \(\overline { WB }\)
\(\overline { ZE }\) and \(\overline { VA }\)
Concurrent Lines:
\(\overline { AB }\), \(\overline { AE }\), \(\overline { AV }\)
\(\overline { BA }\), \(\overline { BC }\), \(\overline { BW }\)
\(\overline { CB }\), \(\overline { CX }\), \(\overline { CD }\)
\(\overline { DC }\), \(\overline { DE }\), \(\overline { DY }\)
\(\overline { EA }\), \(\overline { EZ }\), \(\overline { ED }\)
\(\overline { XC }\), \(\overline { XY }\), \(\overline { XW }\)
\(\overline { YX }\), \(\overline { YZ }\), \(\overline { YD }\)
\(\overline { ZY }\), \(\overline { ZE }\), \(\overline { ZV }\)
\(\overline { VA }\), \(\overline { VW }\), \(\overline { VZ }\)
\(\overline { WB }\), \(\overline { WV }\), \(\overline { WX }\)
Question 3.
Name the following angles as shown in the figure.
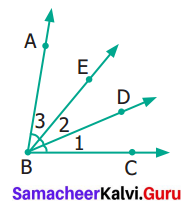
Solution:
(i) ∠1 = ∠CBD or ∠DBC
(ii) ∠2 = ∠DBE or ∠EBD
(iii) ∠3 = ∠ABE or ∠EBA
(iv) ∠1 + ∠2 = ∠CBE or ∠EBC
(v) ∠2 + ∠3 = ∠ABD or ∠DBA
(vi) ∠1 + ∠2 + ∠3 = ∠ABC or ∠CBA
![]()
Question 4.
Measure the angles of the given figures using a protractor and identify the type of angle as acute, obtuse, right or straight.
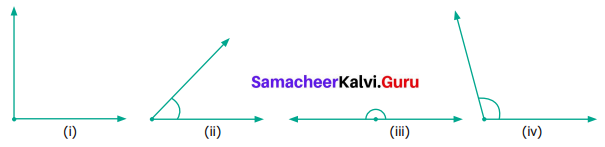
Solution:
(i) 90° – Right Angle
(ii) 45° – Acute Angle
(iii) 180° – Straight Angle
(iv) 105° – Obtuse Angle
Question 5.
Draw the following angles using the protractor.
(i) 45°
(ii) 120°
(iii) 65°
(iv) 135°
(v) 0°
(vi) 180°
(vii) 38°
(viii) 90°
Solution:
(i) 45°
Construction:
1. Drawn the base ray PQ.
2. Placed the centre of the protractor at the vertex P. Lined up the ray \(\overrightarrow{\mathrm{PQ}}\) with the 0° line. Then drawn and labelled a pointed (R) at the 45° mark on the inner scale (a) anticlockwise and (b) outer scale (clockwise)
3. Removed the protractor and drawn at \(\overrightarrow{\mathrm{PR}}\) to complete the angle
Now ∠P = ∠QPR – ∠RPQ = 45°.
(ii) 120°
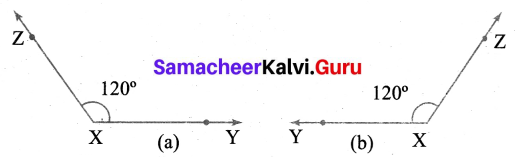
Construction:
1. Placed the centre of the protractor at the vertex X. Lined up the ray \(\overline{\mathrm{XY}}\) with the 0° Line. Then draw and label a point Z at 120° mark on the (a) inner scale (anti-clockwise) and (b) outer scale (clockwise).
2. Removed the protractor and draw \(\overline{\mathrm{XZ}}\) to complete the angle.
Now, ∠X = ∠ZXY = ∠YXZ = 120°.
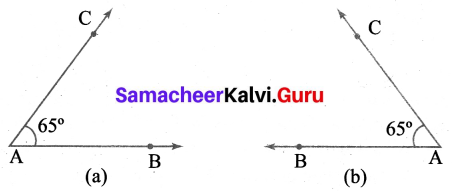
(iii) 65°

Construction:
1. Placed the centre of the protractor at the vertex A. Line up the ray \(\overrightarrow{\mathrm{AB}}\) with the 0° line. Then draw and label a point C at the 65° mark on the (a) inner scale (anti-clockwise) (b) outer scale (clockwise).
2. Removed the protractor and draw \(\overrightarrow{\mathrm{AB}}\) to complete the angle.
Now ∠A = ∠BAC = ∠CAB = 65°.
(iv) 135°

Construction:
1. Placed the centre of the protractor at the Vertex A. Lined up the ray \(\overrightarrow{\mathrm{EG}}\) with the 0° line. Then draw and label a point F at the 135° mark on the (a) inner scale (anti-clockwise) and (b) outer scale (clockwise)
2. Removed the protractor and draw \(\overrightarrow{\mathrm{EF}}\) to complete the angle.
Now ∠E = ∠FEG = ∠GEF = 135°.
(v) 0°

Construction:
1. Placed the centre of the protractor at the vertex G. Lined up the ray \(\overrightarrow{\mathrm{GH}}\) with the 0° line. Then draw and label a point I at the 0° mark on the
(a) inner scale (anti-clockwise)
(b) outer scale (clockwise)
2. Removed the protractor and seen \(\overrightarrow{\mathrm{GI}}\) lies exactly on \(\overrightarrow{\mathrm{GH}}\)
Now ∠G = ∠HGI = ∠IGH = 0°, which is a zero angle.
(vi) 180°
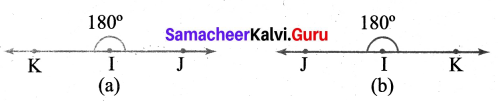
Construction:
1. Placed the centre of the protractor at the vertex I. Lined up the ray \(\overrightarrow{\mathrm{IJ}}\) with the 0° line. Then draw and labelled a point K at the 180° mark on the (a) inner scale (anticlockwise) (b) outer scale (clockwise)
2. Removed the protractor and draw \(\overrightarrow{\mathrm{IK}}\) to complete the angle.
Now ∠I = ∠JHK = ∠KIJ = 180°, which is a straight Angle.
(vii) 38°

Construction:
1. Placed the centre of the protractor at the vertex L. Lined up the ray \(\overrightarrow{\mathrm{LM}}\) with the 0° line. Then draw and label a point N at 38° mark on the (a) inner scale (anticlockwise) and (b) huter scale (clockwise).
2. Removed the protractor and draw \(\overrightarrow{\mathrm{LN}}\) to complete the angle.
Now ∠L = ∠MLN = ∠NLM = 38°.
(viii) 90°

Construction:
1. Placed the centre of the protractor at the vertex ‘O’. Lined up the ray \(\overrightarrow{\mathrm{OP}}\) with the 0° line. Then draw and label a point Q at 90° mark on the (a) inner scale (anticlockwise) and (b) outer scale (clockwise)
2. Removed the protractor and draw \(\overrightarrow{\mathrm{OQ}}\) to complete the angle.
Now ∠O = ∠POQ = ∠QOP = 90°.
![]()
Question 6.
From the figures given below, classify the following pairs of angles into complementary and non-complementary.
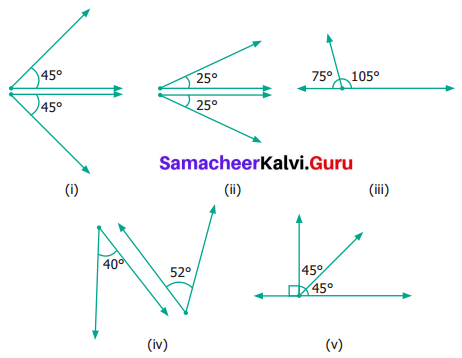
Solution:
(i) and (v) are complementary angles.
(ii), (iii) and (iv) non-complementary angles.
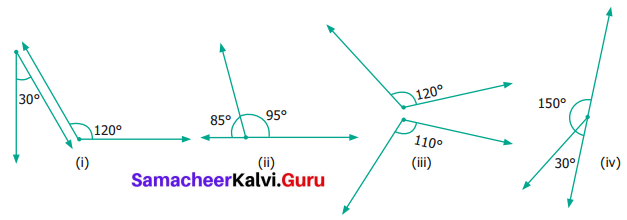
Question 7.
From the figures given below, classify the following pairs of angles into supplementary and non-supplementary.
Solution:
If two angles add up to 180°, then they are supplementary angles.
(a) In (ii) ∠AOB and ∠BOD are supplementary. In (iv) the pair is supplementary
(b) (i) and (iii) are not supplementary.
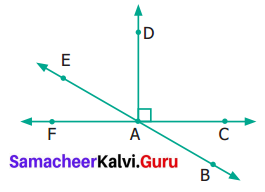
Question 8.
From the figure.
(i) name a pair of complementary angles
(ii) name a pair of supplementary angles
Solution:
(i) ∠FAE and ∠DAE are complementary
(ii) ∠FAD and ∠DAC are supplementary
Question 9.
Find the complementary angle of
(i) 30°
(ii) 26°
(iii) 85°
(iv) 0°
Solution:
When we have an angle, how far we need to go to reach the right angle is called the complementary angle.
(i) Complementary angle of 30° is 90° – 30° = 60°
(ii) Complementary angle of 26° is 90° – 26° = 64°
(iii) Complementary angle of 85° is 90° – 85° = 5°
(iv) Complementary angle of 0° is 90° – 0° = 90°
(v) Complementary angle of 90° is 90° – 90° = 0°
Question 10.
Find the supplementary angle of
- 70°
- 35°
- 165°
- 90°
- 0°
- 180°
- 95°
Solution:
How far we should go in the same direction to reach the straight angle (180°) is called the supplementary angle.
- Supplementary angle of 70° = 180° – 70° = 110°
- Supplementary angle of 35° is 180° – 35° = 145°
- Supplementary angle of 165° is 180° – 165° = 15°
- Supplementary angle of 90° is 180° – 90° = 90°
- Supplementary angle of 0° is 180° – 0° = 180°
- Supplementary angle of 180° is 180° – 180° = 0°
- Supplementary angle of 95° is 180° – 95° = 85°
![]()
Challenging Problems
Question 11.
Think and write and object having.
(i) Parallel Lines
1. _____________
2. _____________
3. _____________
(ii) Perpendicular lines
1. _____________
2. _____________
3. _____________
(iii) Intersecting lines
1. _____________
2. _____________
3. _____________
Solution:
(i) 1. Opposite edges of a Table.
2. Path traced by the wheels of a car on a straight road
3. Opposite edges of a black board
(ii) 1. Adjacent edges of a Table.
2. Hands of the block when it shows 3.30
3. Strokes of the letter ‘L’
(iii) 1. Sides of a triangle
2. Strokes of letter ‘V’
3. Hands of a scissors
Question 12.
Which angle is equal to twice its complement?
Solution:
We know that the sum of complementary angles 90°
Given Angle = 2 × Complementary angle
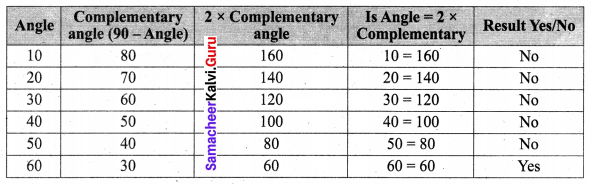
By trial and error, we find that Angle = 2 × Complement for 60°
The required angle = 60°
Another method:
Let the angle be x given
x = 2 (90 – x)
⇒ x = 180 – 2x
⇒ x + 2x = 180
⇒ 3x = 180
⇒ x = 60°
Question 13.
Which angle is equal to two-thirds of its supplement.
Solution:
Supplementary angles sum upto 180°
Given Angle = \(\frac{2}{3}\) × Supplement.
Forming the Table.
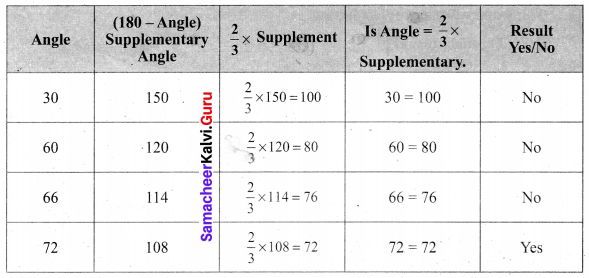
By trial and error, we find that angle = \(\frac{2}{3}\) × supplement for 72°.
The required angle 72°.
Question 14.
Given two angles are supplementary and one angle is 20° more than other. Find the two angles.
Solution:
Given two angles are supplementary i.e. their sum = 180°.
Let the angle be x
Then another angle = x + 20 (given)
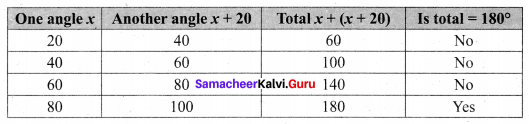
The two angles are 80° and 100°.
Question 15.
Two complementary angles are in the ratio 7 : 2. Find the angles.
Solution:
Total of complementary angles = 90°.
The angles are in the ratio 7 : 2
Dividing total angles to 7 + 2 = 9 equal parts
One angle \(=\frac{7}{9} \times 90=70^{\circ}\)
Another angle \(=\frac{2}{9} \times 90=20^{\circ}\)
Two angles are 70° and 20°.
![]()
Question 16.
Two supplementary angles are in ratio 5 : 4. Find the angles.
Solution:
Let the angles be 5x and 4x
According to the problem
5x + 4x = 180°
9x = 180°
x = \(\frac{180°}{9}\)
x = 20°
∴ Two angles are
(i) 5x = 5 × 20° = 100°
(ii) 4x = 4 × 20° = 80°