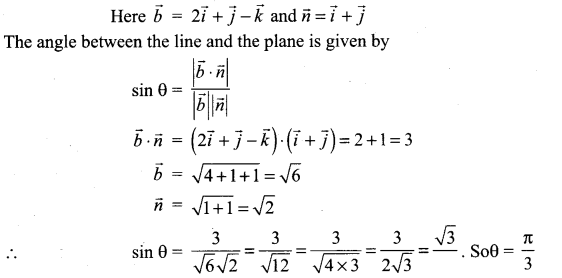You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.9
Question 1.
Find the equation of the plane passing through the line of intersection of the planes \(\vec{r} \cdot(2 \hat{i}-7 \hat{j}+4 \hat{k})\) = 3 and 3x – 5y + 4z + 11 = 0, and the point (-2, 1, 3).
Solution:
The equation of a plane passing throgh the line of intersection of two given planes is
(2x – 7y + 42 – 3) + λ (3x – 5y + 4z +11) = 0
It is passing through (-2, 1, 3)
(-4 – 7 + 12 – 3) + λ(-6 – 5 + 12 + 11) = 0
-2 + λ(12) = 0
12λ = 2
λ = \(\frac { 2 }{ 12 }\) = \(\frac { 1 }{ 6 }\)
The required equation
(2x – 7y + 42 – 3) + \(\frac { 1 }{ 6 }\) (3x – 5y + 4z + 11) = 0
12x – 42y + 24z – 18 + 3x – 5y + 4z + 11 = 0
15x – 47y + 28z – 7 = 0
Question 2.
Find the equation of the plane passing through the line of intersection of the planes x + 2y + 3z = 2 and x – y + z + 11 = 3, and at a distance \(\frac{2}{\sqrt{3}}\) from the point (3, 1, -1).
Solution:
Equation of a plane which passes through the line of intersection of the plane
(x + 2y + 3z – 2) + λ(x – y + z – 3) = 0
(1 + λ)x + (2 – λ)y + (3 + λ)z + (-2 – 3λ) = 0 ………….. (1)

![]()
Question 3.
Find the angle between the line \(\vec{r}=(2 \hat{i}-\hat{j}+\hat{k})+t(\hat{i}+2 \hat{j}-2 \hat{k})\) and the plane \(\vec{r} \cdot(6 \hat{i}+3 \hat{j}+2 \hat{k})\) = 8.
Solution:
The angle between the line and a plane

Question 4.
Find the angle between the planes \(\vec{r} \cdot(\hat{i}+\hat{j}-2 \hat{k})\) = 3 and 2x – 2y + z = 2.
Solution:
The angle between given two planes
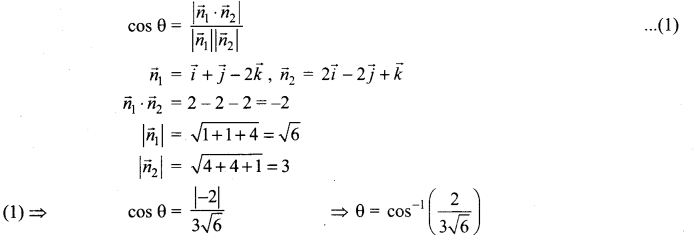
Question 5.
Find the equation of the plane which passes through the point (3, 4, -1)and is parallel to the plane 2x – 3y + 5z + 7 = 0. Also, find the distance between the two planes.
Solution:
Given plane 2x – 3y + 5z +7 = 0 ……… (1)
Parallel plane is 2x – 3y + 5z + k = 0 ………. (2)
It passes through (3, 4, -1)
6 – 12 – 5 + k = 0
-11 + k = 0
k = 11
(2) ⇒ 2x – 3y + 5z + 11 = 0
a = 2, b = -3, c = 5, d1 = 7, d2 = 11
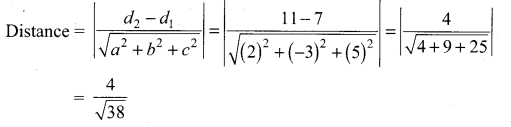
Question 6.
Find the length of the perpendicular from the point (1, -2, 3) to the plane x – y + z = 5.
Solution:
Perpendicular length from the point (x1, y1, z1) to the plane ax + by + cz + d = 0 is
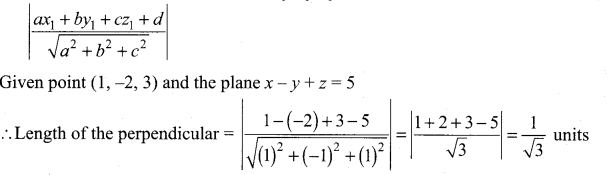
![]()
Question 7.
Find the point of intersection of the line x – 1 = \(\frac{y}{2}\) = z + 1 with the plane 2x – y + 2z = 2. Also, find the angle between the line and the plane.
Solution:
\(\frac { x-1 }{ 1 }\) = \(\frac { y }{ 2 }\) = \(\frac { z+1 }{ 1 }\) = t
(t + 1, 2t, t – 1). It lies on 2x – y + 2z – 2 = 0
2(t + 1) – 2t + 2(t – 1) – 2 = 0
2t + 2 – 2t + 2t – 2 – 2 = 0
2t – 2 = 0
2t = 2
t = 1
∴ Point of intersection is (2, 2, 0)
Angle between the line and the plane is

Question 8.
Find the coordinates of the foot of the perpendicular and length of the perpendicular from the point (4, 3, 2) to the plane x + 2y + 3z = 2
Solution:
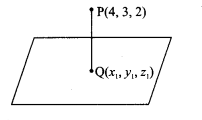
The direction of the normal plane (1, 2, 3)
d.c.s of the PQ is \(\frac{x_{1}-4}{1}=\frac{y_{1}-3}{2}=\frac{z_{1}-2}{3}\) = k
x1 = k + 4, y1 = 2k + 3, z1 = 3k + 2
This passes through the plane x + 2y + 3z = 2
k + 4 + 2(2k + 3) + 3(3k + 2) = 2
k + 4 + 4k + 6 + 9k + 6 = 2
14k = 2 – 16 ⇒ 14k = -14
k = -1
∴ The coordinate of the foot of the perpendicular is (3, 1, -1)
∴ Length of the perpendicular to the plane is
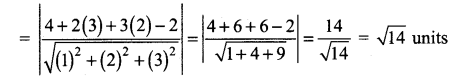
Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.9 Additional Problems
Question 1.
Find the point of intersection of the line passing through the two points (1, 1, – 1); (-1, 0,1) and the xy-plane.
Solution:
The equation of the line passing through (1, 1, -1) and (-1, 0, 1) is
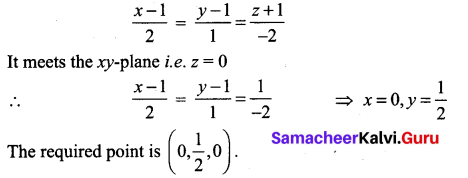
Question 2.
Find the co-ordinates of the point where the line \(\vec{r}=(\vec{i}+2 \vec{j}-5 \vec{k})+t(2 \vec{i}-3 \vec{j}+4 \vec{k})\) meets the plane \(\vec{r} \cdot(2 \vec{i}+4 \vec{j}-\vec{k})\) = 3.
Solution:
The equation of the straight line in the cartesian form is
\(\frac{x-1}{2}=\frac{y-2}{-3}=\frac{z+5}{4}\) = λ (say)
∴ Any point on this line is of the form (2λ + 1, -3λ, + 2, 4λ – 5)
The cartesian equation of the plane is 2x + 4y – z – 3 = 0
But the required point lies on this plane.
∴ 2(2λ + 1) + 4(-3λ + 2) – (4λ – 5 ) – 3 = 0 ⇒ λ = 1
∴ The required point is (3, -1, -1).
Question 3.
Find the point of intersection of the line \(\vec{r}=(\vec{j}-\vec{k})+s(2 \vec{i}-\vec{j}+\vec{k})\) and xz-plane.
Solution:
The given point is (0, 1, -1); parallel vector is \(2 \vec{i}-\vec{j}+\vec{k}\) .
The equation of the line passing through the point (0, 1, -1) and parallel to the vector \(2 \vec{i}-\vec{j}+\vec{k}\) is
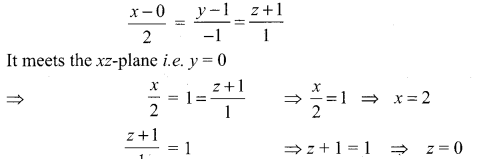
∴ The required point is (2, 0, 0)
![]()
Question 4.
Find the meeting point of the line \(\vec{r}=(2 \vec{i}+\vec{j}-3 \vec{k})+t(2 \vec{i}-\vec{j}-\vec{k})\) and the plane x – 2y + 3z + 7 = 0.
Solution:
The equation of the straight line in cartesian form is
\(\frac{x-2}{2}=\frac{y-1}{-1}=\frac{z+3}{-1}\) = λ (say)
Any point on the line is (2λ, + 2, -λ + 1, λ – 3)
The point lies on the plane x – 2y + 3z + 7 = 0
⇒ 2λ, + 2 – 2(-λ + 1) + 3(-λ, – 3) + 7 = 0 .
2λ + 2 + 2λ – 2 – 3λ – 9 + 7 = 0
λ – 2 = 0 ⇒ λ = 2
So 2λ + 2 = 6; -λ + 1 = -1; -λ – 3 = – 5
∴ The required point is (6, -1, -5)
Question 5.
Show that the following planes are at right angles:
![]()
Solution:
The normal vectors are
\(\bar{n}_{1}=2 \bar{i}-\bar{j}+\bar{k}\) and \(\vec{n}_{2}=+\vec{i}-\vec{j}-3 \vec{k}\)
\(\vec{n}_{1} \cdot \vec{n}_{2}\) = (2)(1) + (-1)(-1) + (1)(-3) = 2 + 1 – 3 = 0
⇒ \(\vec{n}_{1}\) ⊥r to \(\vec{n}_{2}\), i.e., the normals to the planes are at right angles. So, the planes are at right angles.
Question 6.
The planes \(\vec{r} \cdot(2 \vec{i}+\lambda \vec{j}-3 \vec{k})\) = 10 and \(\vec{r} \cdot(\lambda \vec{i}+3 \vec{j}+\vec{k})\) = 5 are perpendicular. Find λ.
Solution:
Since the planes are perpendicular, the angle between the normals = 90°.
The normals are \(\vec{n}_{1}=2 \vec{i}+\lambda \vec{j}-3 \vec{k}\) and \(\vec{n}_{2}=\lambda \vec{i}+3 \vec{j}+\vec{k}\)
\(\vec{n}_{1} \cdot \vec{n}_{2}\) = 0 [∵ θ = π/2]
⇒ (2)(λ) + (λ)(3) + (-3)(1) = 0 ⇒ 2λ + 3λ – 3 = 0
5λ – 3 = 0 ⇒ 5λ = 3 ⇒ λ = 3/5
Question 7.
Find the angle between the line \(\frac{x-2}{3}=\frac{y+1}{-1}=\frac{z-3}{-2}\) and the plane 3x + 4y + z = 0.
Solution:
The angle between the line \(\vec{r}=\vec{a}+t \vec{b}\) and the plane \(\vec{r} \cdot \vec{n}\) = p is given by the formula

![]()
Question 8.
Find the angle between the line \(\vec{r}=\vec{i}+\vec{j}+3 \vec{k}+\lambda(2 \vec{i}+\vec{j}-\vec{k})\) and the plane \(\vec{r} \cdot(\vec{i}+\vec{j})\) = 1,
Solution: