Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.3

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.3

Question 1.
Solve the cubic equation: 2x³ – x² – 18x + 9 = 0 if sum of two of its roots vanishes.
Solution:
2x³ – x² – 18x + 9 = 0
Let the roots be α, β and γ
given α + β = 0
α + β + γ = \(\frac{1}{2}\)
γ = \(\frac{1}{2}\) (∵ α + β = 0)
x² + (α + β)x + αβ = 0, γ = \(\frac{1}{2}\)
x² – 0x + p = 0, (x – \(\frac{1}{2}\)) = 0
(x² + p) = 0, 2x – 1 = 0
∴ (x² + p) (2x – 1) = 2x³ – x² – 18x + 9
2x³ – x² + 2px – p = 2x³ – x² – 18x + 9
-p = 9
p = -9
x² – 9 = 0
x² = 9
x = ± 3
The roots are 3, -3, and \(\frac{1}{2}\)

Question 2.
Solve the equation 9x³ – 36x² + 44x – 16 = 0 if the roots form an arithmetic progression.
Solution:
The given equation is 9x³ – 36x² + 44x – 16 = 0
\(x^{3}-4 x^{2}+\frac{44}{9} x-\frac{16}{9}=0\)
Let the roots be α – d, α, α + d
As they are in A.P

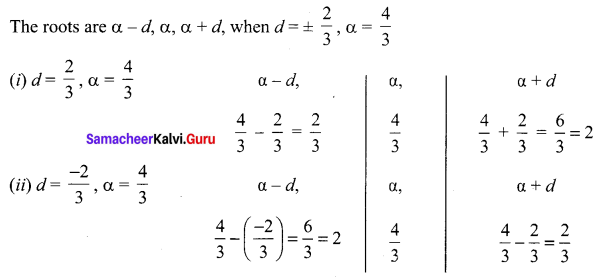
Question 3.
Solve the equation 3x³ – 26x² + 52x – 24 = 0 if its roots form a geometric progression.
Solution:
The given equation is 3x³– 26x² + 52x – 24 = 0
\(x^{3}-\frac{26}{3} x^{2}+\frac{52}{3} x-8=0\)
Given that the root are GP

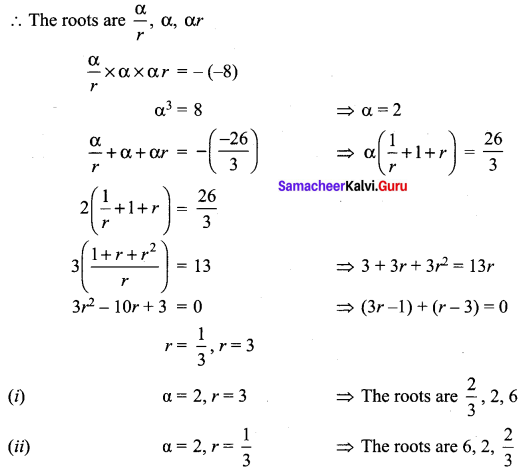
Question 4.
Determine ft and solve the equation 2x³ – 6x² + 3x + k = 0 if one of its roots is twice the sum of the other two roots.
Solution:
The given equation is 2x³ – 6x² + 3x + k = 0

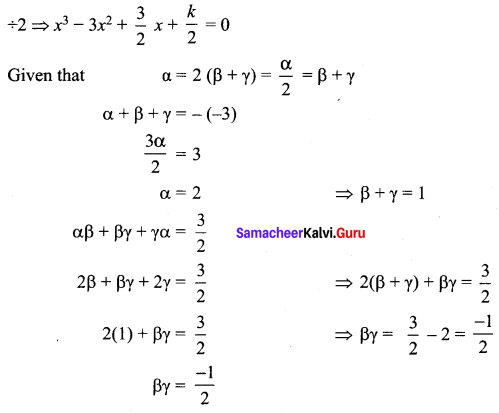
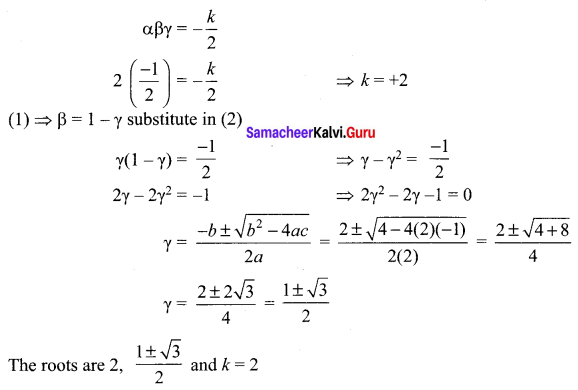
Question 5.
Find all zeros of the polynomial x⁶ – 3x⁵ – 5x⁴ + 22x³ – 39x² – 39x + 135, if it is known that 1 + 2i and √3 are two of its zeros.
Solution:
The given equation is x⁶ – 3x⁵ – 5x⁴ + 22x³ – 39x² – 39x + 135 = 0
The given roots are 1 + 2i, √3
The other roots are 1 – 2i, -√3
The factors are
= {x² – x(2) + (1 + 4)}{(x + √3)(x – √3)}
= (x² – 2x + 5) (x² – 3)
= x⁴ – 3x² – 2x³ + 6x + 5x² – 15
= x⁴ – 2x³ + 2x² + 6x – 15
To find this roots,

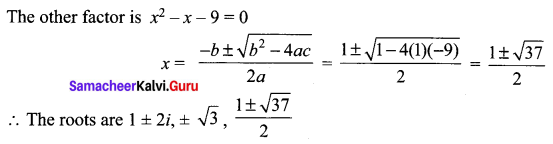
Question 6.
Solve the cubic equations:
(i) 2x³ – 9x² + 10x = 3
(ii) 8x³ – 2x² – 7x + 3 = 0
Solution:
(i) Given equation is 2x³ – 9x² + 10x = 3
Sum of the co-efficients = 0
(x – 1) is a factor.
The other factor is 2x² – 7x + 3
2x² – 7x + 3 = 0
(x – 3)(2x – 1) = 0
The roots are 1, 3, \(\frac { 1 }{ 2 }\)

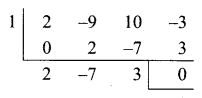
(ii) Given equation is 8x³ – 2x² – 7x + 3 = 0
Sum of odd co-efficients = Sum of even co-efficients
(x + 1) is a factor.
The other factor is 8x² – 10x + 3
8x² – 10x + 3 = 0
(4x – 3) (2x – 1) = 0
The roots are \(\frac{3}{4}, \frac{1}{2},-1\)

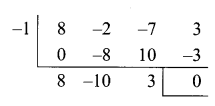
Question 7.
Solve the equation: x⁴ – 14x² + 45 = 0.
Solution:
The given equation is x⁴ – 14x² + 45 = 0
Let x² = y
y² – 14y + 45 = 0
(y – 9)(y – 5) = 0
y = 9, 5
x² = 9, x² = 5
x = ± 3, x = ± √5
The roots are ± 3, ± √5

Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.3 Additional Problems

Question 1.
If one root of x³ + 2x² + 3x + k = 0 is sum of the other two roots then find the value of k.
Solution:
Let α, β, γ be the roots of given equation.
But, α = β + γ
α + β + γ = -2 … (1) ⇒ 2α = -2 ⇒ α = -1
αβ + βγ + γα = 3 … (2) This gives β + γ = – 1
αβγ = -k …(3)

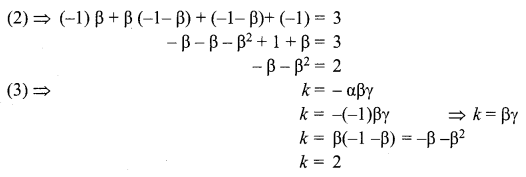
Question 2.
If sum of the roots of the equation x³ – 3x² – 16x + k = 0 is zero then find the value of k.
Solution:
Let α, β, γ be the roots of the given equation.
But, α + β = 0

Question 3.
Find all zeros of the polynomial x³ – 5x² + 9x – 5 = 0, If 2 + i is a root.
Solution: