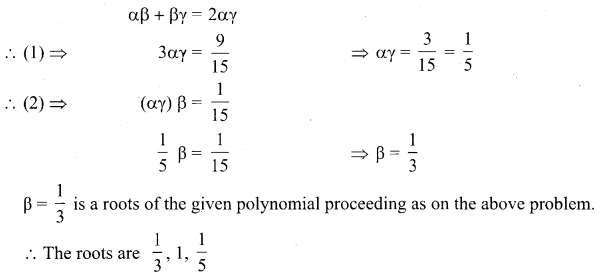Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.2

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.2

Question 1.
If k is real, discuss the nature of the roots of the polynomial equation 2x² + kx + k = 0, in terms of k.
Solution:
Δ = b² – 4ac
a = 2, b = k, c = k
Δ = k² – 4 × 2(k)
Δ = k² – 8k
when k < 0, the polynomial has real roots (Δ > 0)
If Δ = 0 k² – 8k = 0
k(k – 8) = 0
k = 0 or k = 8
When k = 0 or k = 8. The roots are real and equal.
When 0 < k < 8, (Δ < 0) the roots are imaginary.
when k > 8. The roots are real and distinct.

Question 2.
Find a polynomial equation of minimum degree with rational coefficients, having 2 + √3 i as a root.
Solution:
Given roots is (2 + √3 i)
The other root is (2 – √3 i), since the imaginary roots with real co-efficient occur as conjugate pairs.
x² – x(S.O.R) + P.O.R = 0
⇒ x² – x(4) + (4 + 3) = 0
⇒ x² – 4x + 7 = 0

Question 3.
Find a polynomial equation of minimum degree with rational coefficients, having 2i + 3 as a root.
Solution:
Let the root be 3 + 2i
Another root be 3 – 2i
Sum of the roots = 3 + 2i + 3 – 2i = 6
Product of the roots = (3 + 2i) (3 – 2i) = 3² + 2² = 9 + 4 = 13
Required equation is x² – (SR)x + PR = 0
x² – 6x + 13 = 0

Question 4.
Find a polynomial equation of minimum degree with rational coefficients, having √5 – √3 as a root.
Solution:
The given one roots of the polynomial equation are (√5 – √3)
The other roots are (√5 + √3), (-√5 + √3) and (-√5 – √3).
The quadratic factor with roots (√5 – √3) and (√5 + √3) is
= x² – x(S.O.R) + P.O.R
= x² – x(2√5) + (√5 – √3) (√5 + √3)
= x² – 2√5 x + 2
The other quadratic factors with roots (-√5 + √3) (-√5 – √3) is
= x² – x (S.O.R) + P.O.R
= x² – x (-2√5 ) + (5 – 3)
= x² + 2√5x + 2
To rationalize the co-efficients with minimum degree
(x² – 2√5 x + 2) (x² + 2√5 x + 2) = 0
⇒ (x² + 2)² – (2√5 x)² = 0
⇒ x⁴ + 4 + 4x² – 20x² = 0
⇒ x⁴ – 16x² + 4 = 0

Question 5.
Prove that a straight line and parabola cannot intersect at more than two points.
Solution:
let be the equation of a straight line y = mx + c
Let be the equation of a parabola y² = 4ax
(mx + c)² = 4ax
m²x² + 2mcx + c² – 4ax = 0
m²x² + (2x)(mc – 2a) + c² = 0
Which is a quadratic equation.
It can not have more than two solutions.

Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.2 Additional Problems

Question 1.
Find a polynomial equation of minimum degree with rational co-efficients having 1 – i as a root.
Solution:
Given root is 1 – i
The other root is 1 + i
Sum of the roots: 1 – i + 1 + i = 2
product of the roots: (1 – i) (1 + i) = (1)² + (1)² ⇒ 1 + 1 = 2
∴ The required polynomial equation of minimum degree with rational coefficients is
x² – x (S.R.) + (P.R.) = 0
x² – 2x + 2 = 0

Question 2.
Find a polynomial equation of minimum degree with rational coefficients having \(\sqrt{3}+\sqrt{7}\) as a root.
Solution:

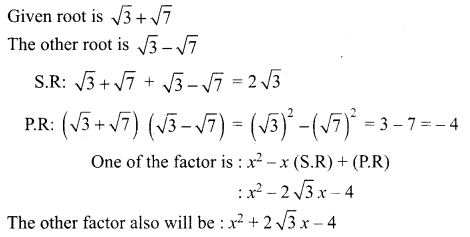
The required polynomial equation of minimum degree

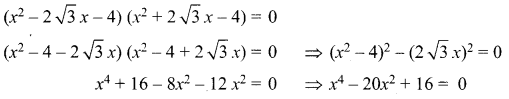
Question 3.
If the roots of the equation x³ + px² + qx + r = 0 are in A.P then show that 2p³ – 9pq + 27 r = 0.
Solution:
Let the roots of the given equation is a – d, a, a + d

Question 4.
Solve 27x³ + 42x² – 28x -8 = 0 given that its roots are in geometric progressive.
Solution:

Question 5.
Solve the equation 15x³ – 23x² + 9x – 1 = 0. Where roots are in H.P.
Solution: