You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.8
Question 1.
If to ω ≠ 1 is a cube root of unity, then show that \(\frac{a+b \omega+c \omega^{2}}{b+c \omega+a \omega^{2}}+\frac{a+b \omega+c \omega^{2}}{c+a \omega+b \omega^{2}}=1\)
Solution:
Since ω is a cube root of unity, we have ω3 = 1 and 1 + ω + ω2 = 0
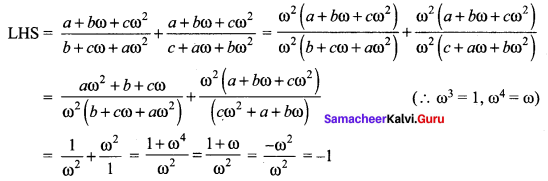
![]()
Question 2.
Show that \(\left(\frac{\sqrt{3}}{2}+\frac{i}{2}\right)^{5}+\left(\frac{\sqrt{3}}{2}-\frac{i}{2}\right)^{5}=-\sqrt{3}\)
Solution:


Question 3.
Find the value of \(\left(\frac{1+\sin \frac{\pi}{10}+i \cos \frac{\pi}{10}}{1+\sin \frac{\pi}{10}-i \cos \frac{\pi}{10}}\right)^{10}\)
Solution:
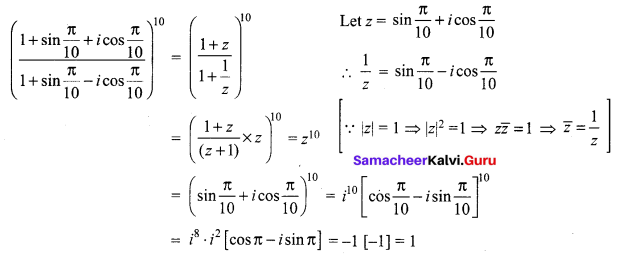
Question 4.
If 2 cos α = x + \(\frac{1}{x}\) and 2 cos β = y + \(\frac{1}{y}\), show that

Solution:
(i) 2 cos α = x + \(\frac{1}{x}\)
⇒ 2 cos α = \(\frac{x^{2}+1}{x}\)
⇒ 2x cos α = x2 + 1
⇒ x2 – 2x cos α + 1 = 0
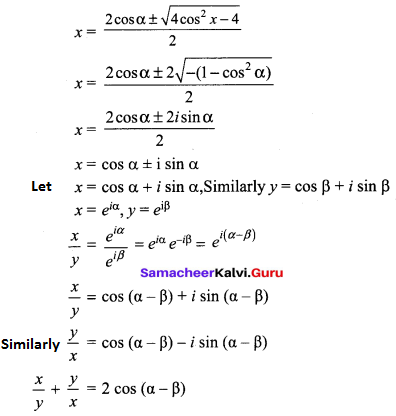

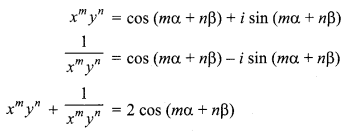
![]()
Question 5.
Solve the equation z3 + 27 = 0
Solution:
z3 + 27 = 0
⇒ z3 = -27
⇒ z3 = 33(-1)
⇒ z = 3(-1)1/3

Question 6.
If ω ≠ 1 is a cube root of unity, show that the roots of the equation (z – 1)3 + 8 = 0 are -1, 1 – 2ω, 1 – 2ω2
Solution:
(z – 1)3 + 8 = 0
⇒ (z – 1 )3 = -8

The roots are -1, 1 – 2ω, 1 – 2ω2
Question 7.
Find the value of \(\sum_{k=1}^{8}\left(\cos \frac{2 k \pi}{9}+i \sin \frac{2 k \pi}{9}\right)\)
Solution:
\(\sum_{k=1}^{8}\left(\cos \frac{2 k \pi}{9}+i \sin \frac{2 k \pi}{9}\right)\)
We know that 9th roots of unit are 1, ω, ω2, ……., ω8
Sum of the roots:
1 + ω + ω2 + …. + ω8 = 0 ⇒ ω + ω2 + ω3 + …… + ω8 = -1

The sum of all the terms \(\sum_{k=1}^{8}\left(\cos \frac{2 k \pi}{9}+i \sin \frac{2 k \pi}{9}\right)\) = -1
Question 8.
If ω ≠ 1 is a cube root of unity, show that
(i) (1 – ω + ω2)6 + (1 + ω – ω2)6 = 128
(ii) (1 + ω)(1 + ω2)(1 + ω4)(1 + ω8)……(1 + ω2n) = 1
Solution:
(i) (1 – ω + ω²)6 + (1 + ω – ω²)6
= (-ω + ω)6 + (-ω – ω²)6
= (-2ω)6 + (-2ω²)6
= 26 [ω6 + ω12] [∵ ω6 = 1]
= 64 [1 + 1]
= 64 × 2
= 128
(ii) (1 – ω) (1 + ω²) (1 + ω) (1 + ω2) ….. 2n factors
(-ω²) (-ω) (-ω²) (-ω) ……. 2n factor
(ω³) (ω³) …… 2n factor
= 1.1 …….. 2n factor
= 1
Question 9.
If z = 2 – 2i, find the rotation of z by θ radians in the counter clockwise direction about the origin when
(i) θ = \(\frac{\pi}{3}\)
(ii) θ = \(\frac{2 \pi}{3}\)
(iii) θ = \(\frac{3 \pi}{2}\)
Solution:
(i) z = 2 – 2i = 2 (1 – i) = r(cos θ + i sin θ)
\(r=\sqrt{x^{2}+y^{2}}=2 \sqrt{1+1}=2 \sqrt{2}\)
\(\alpha=\tan ^{-1}=\left|\frac{y}{x}\right|=\tan ^{-1}|1|=\frac{\pi}{4}\)
(1 – i) lies in IV quadrant
θ = -α = \(-\frac{\pi}{4}\)
\(\Rightarrow z=2 \sqrt{2}\left[\cos \left(\frac{-\pi}{4}\right)+i \sin \left(\frac{-\pi}{4}\right)\right]\)
z is rotated by θ = \(\frac{\pi}{3}\) in the counter clock wise direction.
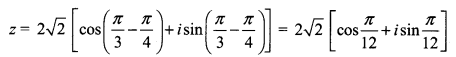
(ii) z is rotated by θ = \(\frac{2 \pi}{3}\) in the counter clockwise direction.
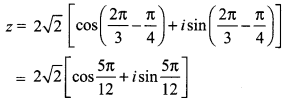
(iii) z is rotated by θ = \(\frac{3 \pi}{2}\) in the counter clockwise direction.
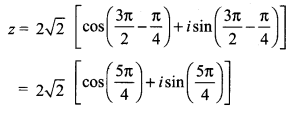
![]()
Question 10.
Prove that the values of \(\sqrt[4]{-1} \text { are } \pm \frac{1}{\sqrt{2}}(1 \pm i)\)
Solution:

The roots are \(\pm \frac{1}{\sqrt{2}}(1 \pm i)\)
Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.8 Additional Problems
Question 1.

Solution:

Question 2.
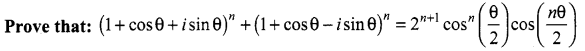
Solution:
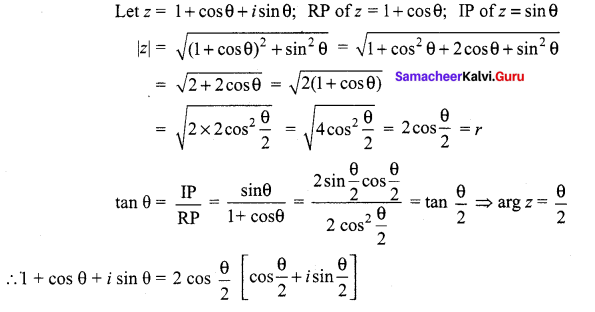
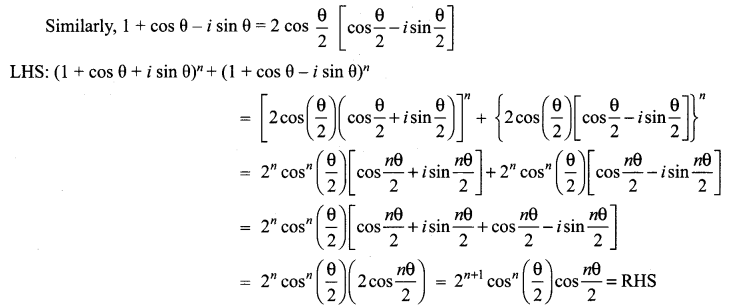
Question 3.
Prove that: (1 + i)4n and (1 + i)4n + 2 are real and purely imaginary respectively.
Solution:
Let z = 1 + i
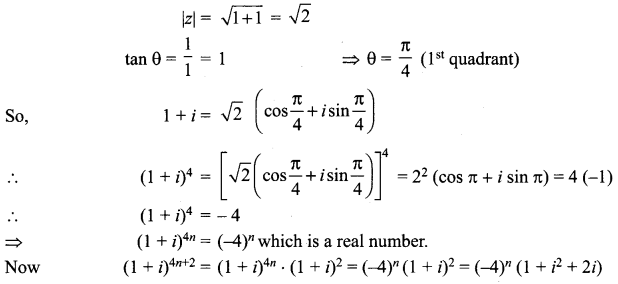
= 2i (-1)n which is purely imaginary.
![]()
Question 4.
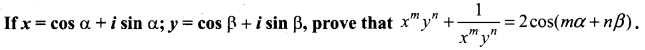
Solution:

Question 5.
If a = cos 2α + i sin 2α, b = cos 2β + i sin 2β and c = cos 2γ + i sin 2γ, prove that
![]()
Solution:
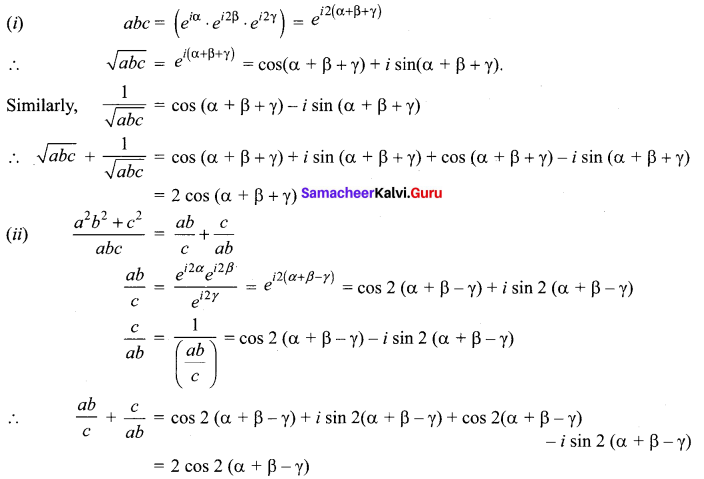
Question 6.
Solve: x4 + 4 = 0
Solution:

Question 7.
If x = a + b, y = aω + bω2, z = aω2 + bω, show that
(i) xyz = a3 + b3
(ii) x3 + y3 + z3 = 3(a3 + b3)
Solution:
(i) x = a + A; y = aω + bω2, z = aω2 + bω
Now xyz = (a + b) (aω + bω2) (abω2 + bω) = (a+A) [aω3 + abω2 + abω + b2ω3]
= (a + b) (a2 – ab + b2) = a3 + b3
xyz = a3 + b3
(ii) x = a + b, y = aω + bω2, z = aω2 + bω
x + y + z = (a + aω + aω2) + (b + bω2 + bω)
= a (1 + ω + ω2) + b (1 + ω + ω2) = a(0) + b(0) = 0
Now x + y + z = 0 ⇒ x3 + y3 + z3 = 3xyz
Here xyz = a3 + b3
∴ x3 + y3 + z3 = 3 (a3 + b3)