You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 11 Probability Distributions Ex 11.5
Question 1.
Compute P(X = k) for the binomial distribution, B(n, p) where
![]()
Solution:

Question 2.
The probability that Mr. Q hits a target at any trial is \(\frac{1}{4}\). Suppose he tries at the target 10 times. Find the probability that he hits the target
(i) exactly 4 times
(ii) at least one time.
Solution:
Let ‘p’ be the probability of hitting the trial
![]()
and number of trials ‘n’ = 10
Probability of ‘x’ success in ‘n’ trials is
![]()
![]()
(i) Probability that Mr.Q hits the target exactly 4 times is
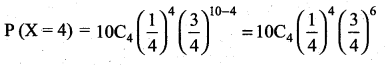
(ii) Probability that Mr.Q hits the target atleast one time is
P(X ≥ 1) = 1 – P(X < 1)
= 1 – P(X = 0)
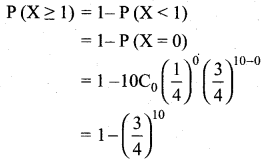
Question 3.
Using binomial distribution find the mean and variance of X for the following experiments
(i) A fair coin is tossed 100 times, and X denote the number of heads.
(ii) A fair die is tossed 240 times, and X denote the number of times that four appeared.
Solution:
(i) n = 100, ‘X’ denotes the number of heads.
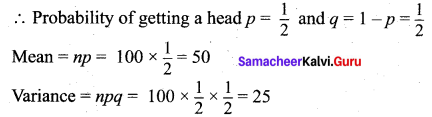
(ii) n = 240, ‘X’ denotes the number of times four appeared.
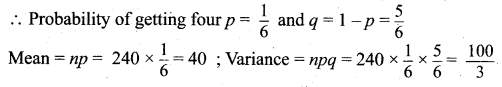
![]()
Question 4.
The probability that a certain kind of component will survive a electrical test is \(\frac{3}{4}\). Find the probability that exactly 3 of the 5 components tested survive.
Solution:
Given n = 5

Question 5.
A retailer purchases a certain kind of electronic device from a manufacturer. The manufacturer indicates that the defective rate of the device is 5%. The inspector of the retailer randomly picks 10 items from a shipment. What is the probability that there will be
(i) at least one defective item
(ii) exactly two defective items.
Solution:
Given n = 10
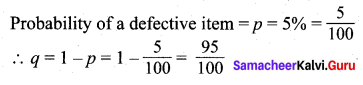
Let ‘X’ be the random variable denotes the number of defective items.
∴ Probability of ‘x’ successes in ‘n’ trials is

![]()
Question 6.
If the probability that fluorescent light has a useful life of at least 600 hours is 0.9, find the probabilities that among 12 such lights.
(i) exactly 10 will have a useful life of at least 600 hours;
(ii) at least 11 will have a useful life of at least 600 hours;
(iii) at least 2 will not have a useful life of at least 600 hours.
Solution:
Given n = 12
Probability that a fluorescent light has a life of atleast of 600 hours is p = 0.9
∴ q = 1 – p = 1 – 0.9 = 0.1
Let ‘X’ be the number of bulbs.
∴ The probability of ‘x’ successes in ‘n’ trials is
![]()
(i) Probability that exactly 10 bulbs will have a useful life of atleast 600 hours
![]()
(ii) Probability that atleast 11 will have a useful life of atleast 600 hours is
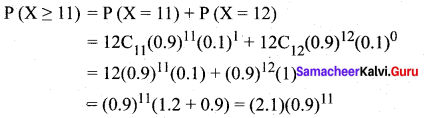
(iii) Probability that atleast 2 will not have a useful life of 600 hours is

Question 7.
The mean and standard deviation of a binomial variate X are respectively 6 and 2. Find
(i) the probability mass function
(ii) P(X = 3)
(iii) P(X ≥ 2) .
Solution:


![]()
Question 8.
If X ~ B(n, p) such that 4P(X = 4) = P(x = 2) and n = 6. Find the distribution, mean and standard deviation.
Solution:

Question 9.
In a binomial distribution consisting of 5 independent trials, the probability of 1 and 2 successes are 0.4096 and 0.2048 respectively. Find the mean and variance of the distribution.
solution:
Number of trials n = 5
The probability of ‘x’ successes in ‘n’ trials is
![]()
Given P(X = 1) = 0.4096 and P (X = 2) = 0.2048
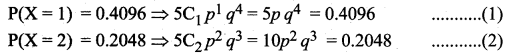
Dividing Eq.(1) by Eq.(2)

Samacheer Kalvi 12th Maths Solutions Chapter 11 Probability Distributions Ex 11.5 Additional Problems
Question 1.
In a Binomial distribution if n = 5 and P(X = 3) = 2P(X = 2) find p.
Solution:
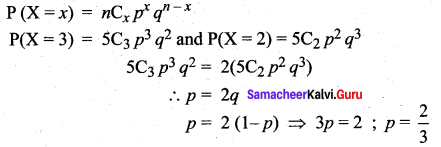
![]()
Question 2.
If the sum of mean and variance of a Binomial Distribution is 4.8 for 5 trials find the distribution.
Solution:
np + npq = 4.8 ⇒ np (1 + q) = 4.8
5p [1 + (1 – p)] = 4.8
p2 – 2p + 0.96 = 0 ⇒ p = 1.2, 0.8
∴ p = 0.8 ; q = 0.2 [∵ p cannot be greater than 1]
∴ The Binomial distribution is P[X = x] = 5Cx (0.8)x (0.2)5 – x, x = 0 to 5
Question 3.
If on an average 1 ship out of 10 do not arrive safely to ports. Find the mean and the standard deviation of the ships returning safely out of a total of 500 ships.
Solution:
Probability of a ship arriving safely

Question 4.
The overall percentage of passes in a certain examination is 80. If six candidates appear in the examination what is the probability that at least five pass the examination.
Solution:
Pass percentage = 80%
∴ Probability of a candidate passing in the examination
![]()

![]()
Question 5.
In a hurdle race, a player has to cross 10 hurdles. The probability that he will clear each hurdle is 5/6. What is the probability that he will knock down less than 2 hurdles?
Solution:
