You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.8
Choose the correct or the most suitable answer from the given four alternatives.
Question 1.
If |adj(adj A)| = |A|9, then the order of the square matrix A is _______
(a) 3
(b) 4
(c) 2
(d) 5
Answer:
(b) 4
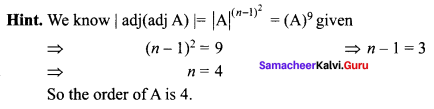
Question 2.
If A is a 3 × 3 non-singular matrix such that AAT = ATA and B = A-1AT, then BBT = ______
(a) A
(b) B
(c) I3
(d) BT
Answer:
(c) I3
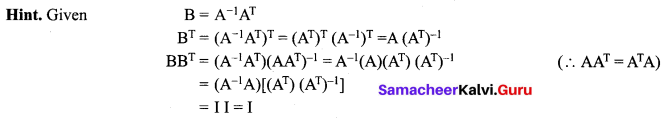
Question 3.

Answer:

![]()
Question 4.
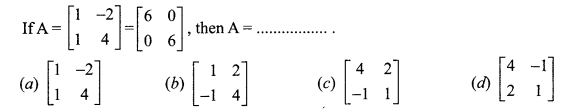
Answer:
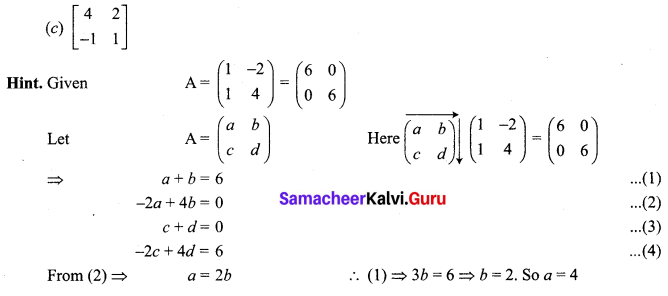

Question 5.

Answer:

Question 6.
If A = \(\left[\begin{array}{ll}{2} & {0} \\ {1} & {5}\end{array}\right]\) and B = \(\left[\begin{array}{ll}{1} & {4} \\ {2} & {0}\end{array}\right]\) then |adj(AB)| = _______
(a) -40
(b) -80
(c) -60
(d) -20
Answer:
(b) -80
Hint:
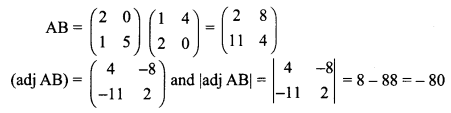
Question 7.
If P = \(\left[\begin{array}{ccc}{1} & {x} & {0} \\ {1} & {3} & {0} \\ {2} & {4} & {-2}\end{array}\right]\) is the adjoint of 3 × 3 matrix A and |A| = 4, then x is ______
(a) 15
(b) 12
(c) 14
(d) 11
Answer:
(d) 11
Hint: Given |A| = 4 and P is the adjoint matrix of A
|P| = 42 = 16
⇒ -2 (3 – x) = 16
⇒ -6 + 2x = 16
⇒ 2x = 22
⇒ x = 11
Question 8.
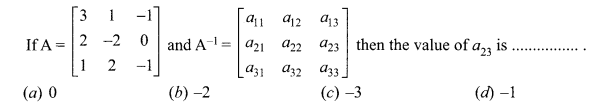
Answer:

![]()
Question 9.
If A, B and C are invertible matrices of some order, then which one of the following is not true?
(a) adj A =|A| A-1
(b) adj(AB) = (adj A) (adj B)
(c) det A-1 = (det A)-1
(d) (ABC)-1 = C-1B-1A-1
Answer:
(b) adj(AB) = (adj A) (adj B)
Question 10.
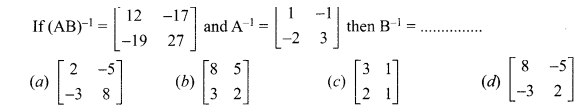
Answer:

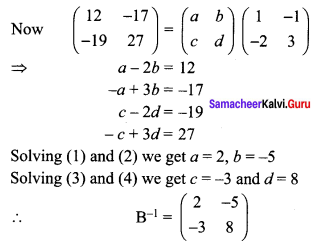
Question 11.
If AT A-1 is symmetric, then A2 = _______
(a) A-1
(b) (AT)2
(c) AT
(d) (A-1)2
Answer:
(b) (AT)2

Question 12.
If A is a non-singular matrix such that \(A^{-1}=\left[\begin{array}{rr}{5} & {3} \\ {-2} & {-1}\end{array}\right]\), then (AT)-1 = _______

Answer:
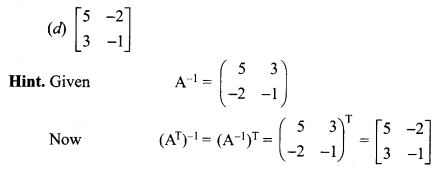
Question 13.

Answer:
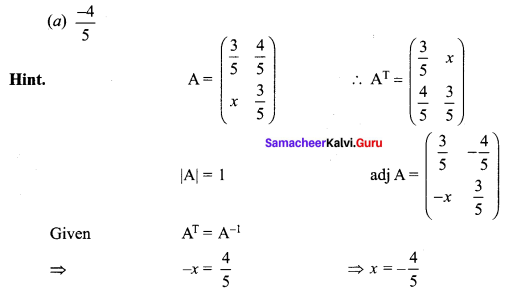
Question 14.

Answer:
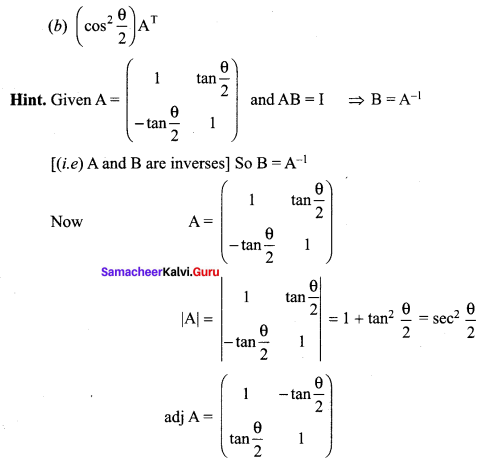
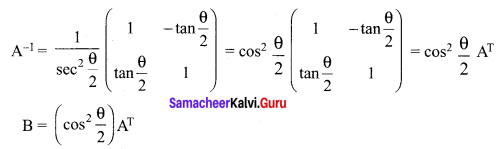
![]()
Question 15.
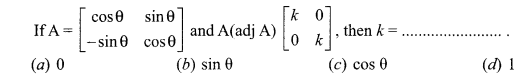
Answer:

Question 16.
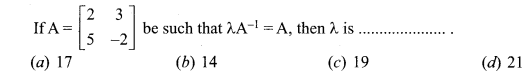
Answer:

Question 17.
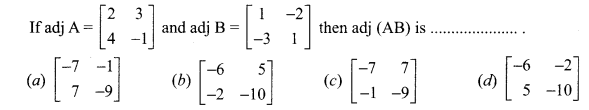
Answer:
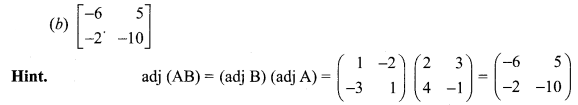
Question 18.
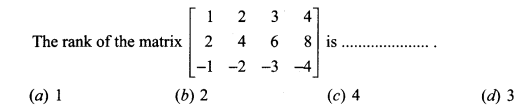
Answer:
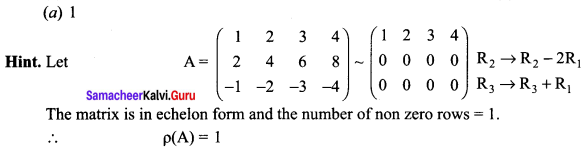
Question 19.
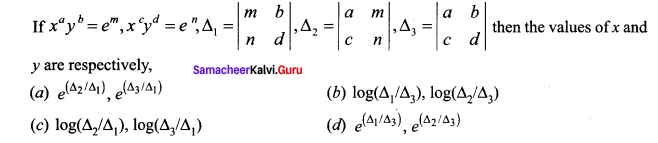
Answer:

![]()
Question 20.
Which of the following is/are correct?
(i) Adjoint of a symmetric matrix is also a symmetric matrix
(ii) Adjoint of a diagonal matrix is also a diagonal matrix.
(iii) If A is a square matrix of order n and λ, is a scalar, then adj(λA) = λn adj(A).
(iv) A(adj A) = (adj A)A = |A| I
(a) Only (i)
(b) (ii) and (iii)
(c) (iii) and (iv)
(d) (i), (ii) and (iv)
Answer:
(d) (i), (ii) and (iv)
Question 21.
If ρ(A) = ρ([A|B]), then the system AX = B of linear equations is ______
(a) consistent and has a unique solution
(b) consistent
(c) consistent and has infinitely many solution
(d) inconsistent
Answer:
(b) consistent
Question 22.
If 0 ≤ θ ≤ π, the system of equations x + (sin θ)y – (cos θ)z = 0, (cos θ)x – y + z = 0, (sin θ)x + y – z = 0 has a non-trivial solution then θ is ______
(a) \(\frac{2 \pi}{3}\)
(b) \(\frac{3 \pi}{4}\)
(c) \(\frac{5 \pi}{4}\)
(d) \(\frac{\pi}{4}\)
Answer:
(d) \(\frac{\pi}{4}\)

Question 23.
The augmented matrix of a system of linear equations is \(\left[\begin{array}{cccc}{1} & {2} & {7} & {3} \\ {0} & {1} & {4} & {6} \\ {0} & {0} & {\lambda-7} & {\mu+5}\end{array}\right]\). The system has infinitely many solutions if _____
(a) λ = 7, μ ≠ 5
(b) λ = -7, μ = 5
(c) λ ≠ 7, μ ≠ -5
(d) λ = 7, μ = -5
Answer:
(d) λ = 7, μ = -5
Question 24.
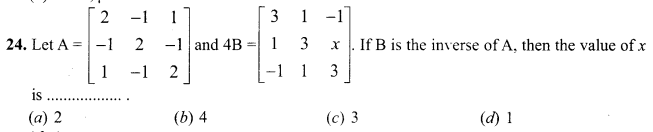
Answer:
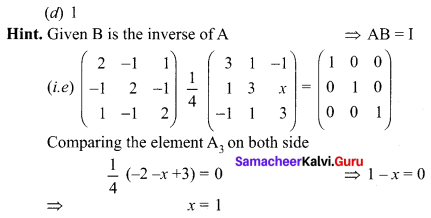
Question 25.

Answer:
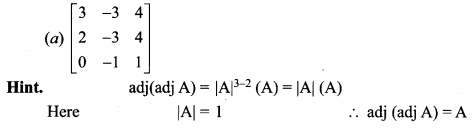
![]()
Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.8 Additional Problems
Question 1.
![]()
(a) m < n (b) m > n
(c) m = n
(d) None of these
Solution:
(c) m = n
Hint:
A = [aij]m×n is a square matrix if number of rows is equal to that of columns, i.e., m = n.
Question 2.
Matrices A and B will be inverse of each other only if ……..
(a) AB = BA
(b) AB = BA = O
(c) AB = O, BA = I
(d) AB = BA = I
Solution:
(d) AB = BA = I
Hint:
By the definition of invertible matrices two matrices A and B are inverse of each other if AB = BA = I.
Question 3.
If A is an invertible matrix of order 2 then det (A-1) is equal to

Solution:
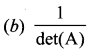
Hint.

Question 4.
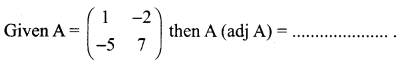
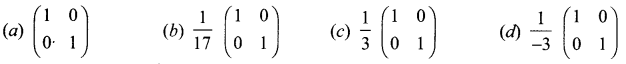
Solution:
(d) \(\frac{1}{-3}\left(\begin{array}{ll}{1} & {0} \\ {0} & {1}\end{array}\right)\)
Question 5.
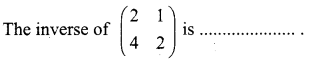

Solution:
(d) Inverse does not exist
![]()
Question 6.
Given ρ(A, B) = ρ(A) = number of unknowns, then the system has …….
(a) unique solution
(b) no solution
(c) inconsistent
(d) infinitely many solution
Solution:
(a) unique solution
Question 7.
Given ρ(A, B) ≠ ρ(A) then the system has
(a) no solution
(b) unique solution
(c) infinitely many solution
(d) None
Solution:
(a) no solution
Question 8.
Given ρ(A, B) = ρ(A) < number of unknowns, then the system has …….
(a) unique solution
(b) no solution
(c) 3 solutions
(d) infinitely many solution
Solution:
(d) infinitely many solution
Question 9.
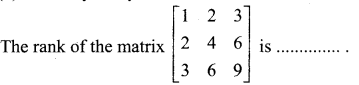
(a) 1
(b) 2
(c) 3
(d) None of these
Solution:
(a) 1
Question 10.
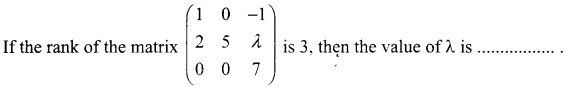
(a) 1
(b) 0
(c) 4
(d) any real number
Solution:
(d) any real number
Question 11.
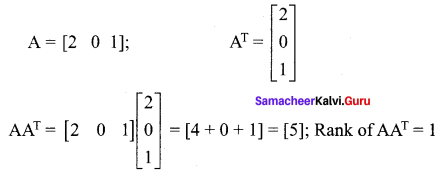
If A = [2 0 1], then the rank of AAT is ………
(a) 1
(b) 2
(c) 3
(d) 0
Solution:
(a) 1
Hint.
Question 12.
If the rank of the matrix 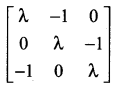 is 2, then λ is ……
is 2, then λ is ……
(a) 1
(b) 2
(c) 3
(d) any real number
Solution:
(a) 1
Hint.
Since the rank of the given matrix is 2, the value of 3rd order determinant is zero.

Question 13.
If A is a scalar matrix with scalar k ≠ 0, of order 3, then A-1 is …….

Solution:
\(\frac{1}{k} \mathrm{I}\)
Hint:
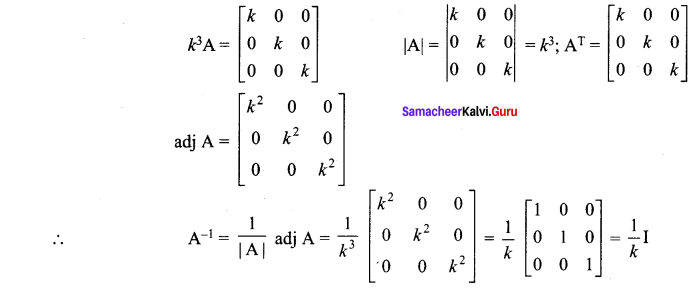
![]()
Question 14.


Solution:
Hint:
(adj A)(A) = |A|I
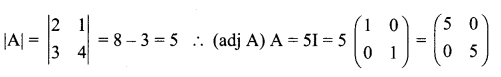
Question 15.
If A is a square matrix of order n, then |adj A| is …….
(a) |A|2
(b) |A|n
(c) |A|n – 1
(d) |A|
Solution:
(c) |A|n – 1
Hint:
When A is square matrix of order 3, then |adj A| = |A|2 = |A|3 – 1 ∴ When A is a square matrix of order n, |adj A| = |A|n – 1
Question 16.
If A is a matrix of order 3, then det (kA)
(a) k3(det A)
(b) k2(det A)
(c) k(det A)
(d) det (A)
Solution:
(a) k3(det A)
Hint:
A is a matrix of order 3. ∴ det (kA) = k3 (det A)
Question 17.
If I is the unit matrix of order n, where k ± 0 is a constant, then adj(kI) = …….
(a) kn(adj I)
(b) k(adj I)
(c) k2(adj I)
(d) kn – 1 (adj I)
Solution:
(d) kn – 1 (adj I)
Hint:
When I is a unit matrix of order 3, then adj (kI) = k2 (adj I)
∴ When I is a unit matrix of order n, then adj (kI) = kn – 1 (adj I)
Question 18.
In a system of 3 linear non-homogeneous equations with three unknowns, if ∆ = 0 and ∆x = 0, ∆y ≠ 0 and ∆z = 0, then the system has …..
(a) unique solution
(b) two solutions
(c) infinitely many solutions
(d) no solution
Solution:
(d) no solution
Hint:
When ∆ = 0 ∆x, ∆z = 0 but ∆y ≠ 0 ⇒ that the system is inconsistent.
∴ There is no solution.