You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.1
Question 1.
Find the adjoint of the following:
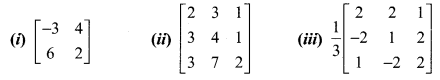
Solution:

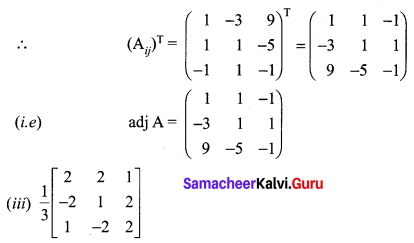
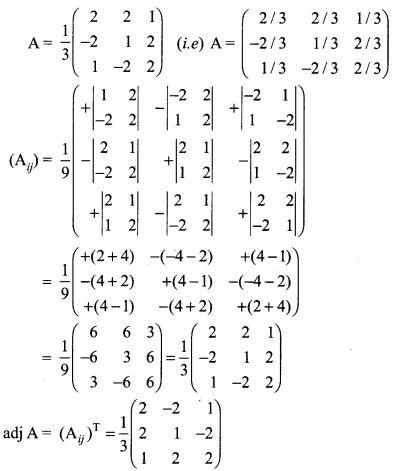
![]()
Question 2.
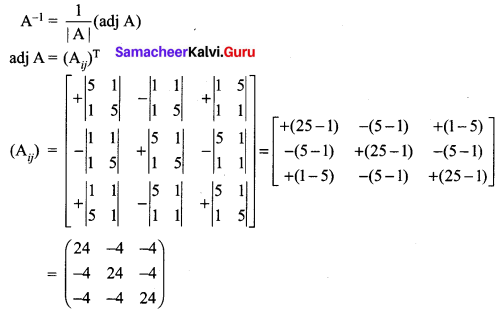
Find the inverse (if it exists) of the following:
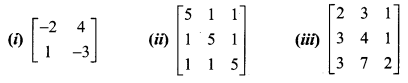
Solution:
For a matrix A, \(\mathrm{A}^{-1}=\frac{1}{|\mathrm{A}|}(\mathrm{adj} \mathrm{A})\). Where |A| ≠ 0. If |A| = 0 then A is called a singular matrix and so \(\mathrm{A}^{-1}\) does not exist.



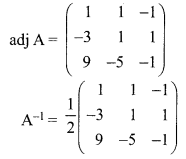
Question 3.
If F(α) = \(\left[\begin{array}{ccc}{\cos \alpha} & {0} & {\sin \alpha} \\ {0} & {1} & {0} \\ {-\sin \alpha} & {0} & {\cos \alpha}\end{array}\right]\) show that \([\mathrm{F}(\alpha)]^{-1}=\mathrm{F}(-\alpha)\)
Solution:
Let A = F (α)
So \([\mathrm{F}(\alpha)]^{-1}=\mathrm{A}^{-1}\)
Now
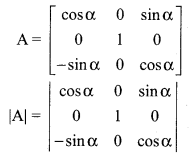


![]()
Question 4.
If A = \(\left[\begin{array}{cc}{5} & {3} \\ {-1} & {-2}\end{array}\right]\) show that A2 – 3A – 7I2 = O2. Hence find A-1.
Solution:
A = \(\left[\begin{array}{cc}{5} & {3} \\ {-1} & {-2}\end{array}\right]\)
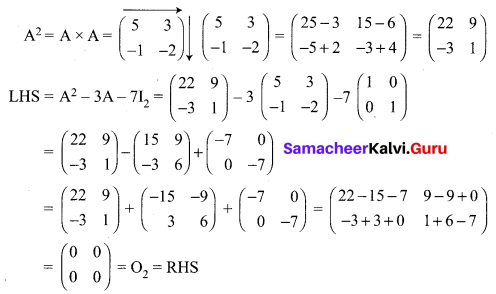
To Find A-1
Now we have proved that A2 – 3A – 7I2 = O2
Post multiply by A-1 we get
A – 3I – 7A-1 = O2
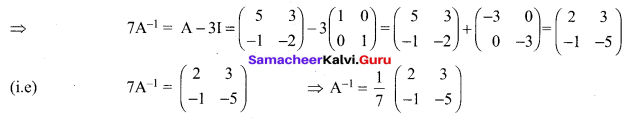
Question 5.
If \(\mathbf{A}=\frac{1}{9}\left[\begin{array}{ccc}{-8} & {1} & {4} \\ {4} & {4} & {7} \\ {1} & {-8} & {4}\end{array}\right]\) prove that A-1 = AT
Solution:



Question 6.
If \(\mathbf{A}=\left[\begin{array}{rr}{8} & {-4} \\ {-5} & {3}\end{array}\right]\), verify that A(adj A) = (adj A)A = |A| I2
Solution:


Question 7.
If \(\mathbf{A}=\left[\begin{array}{ll}{3} & {2} \\ {7} & {5}\end{array}\right]\), and \(\mathbf{B}=\left[\begin{array}{cc}{-1} & {-3} \\ {5} & {2}\end{array}\right]\) verify that (AB)-1 = B-1 A-1.
Solution:

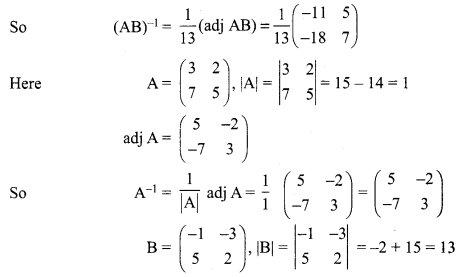

![]()
Question 8.
If adj (A) = \(\left[\begin{array}{ccc}{2} & {-4} & {2} \\ {-3} & {12} & {-7} \\ {-2} & {0} & {2}\end{array}\right]\) find A
Solution:



Question 9.
If adj(A) = \(\left[\begin{array}{ccc}{0} & {-2} & {0} \\ {6} & {2} & {-6} \\ {-3} & {0} & {6}\end{array}\right]\) find A-1
Solution:

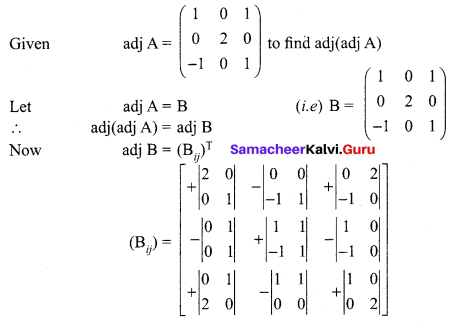
Question 10.
Find adj(adj(A)) if adj A = \(\left[\begin{array}{ccc}{1} & {0} & {1} \\ {0} & {2} & {0} \\ {-1} & {0} & {1}\end{array}\right]\)
Solution:

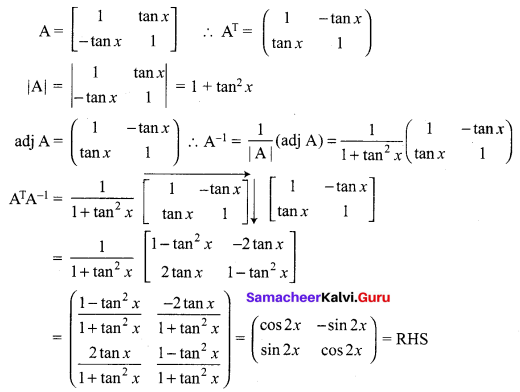
Question 11.

Solution:
Question 12.
Find the matrix A for which A \(\left[\begin{array}{cc}{5} & {3} \\ {-1} & {-2}\end{array}\right]=\left[\begin{array}{cc}{14} & {7} \\ {7} & {7}\end{array}\right]\)
Solution:
Given A \(\left[\begin{array}{cc}{5} & {3} \\ {-1} & {-2}\end{array}\right]=\left[\begin{array}{cc}{14} & {7} \\ {7} & {7}\end{array}\right]\)
Let \(\mathrm{B}=\left(\begin{array}{cc}{5} & {3} \\ {-1} & {-2}\end{array}\right) \text { and } \mathrm{C}=\left(\begin{array}{cc}{14} & {7} \\ {7} & {7}\end{array}\right)\)
Given AB = C, To find A
Now AB = C
Post multiply by B-1 on both sides
ABB-1 = CB-1 (i.e) A (BB-1) = CB-1
⇒ A(I) = CB-1 (i.e) A = CB-1
To find B-1:

Question 13.
Given \(\mathbf{A}=\left[\begin{array}{cc}{1} & {-1} \\ {2} & {0}\end{array}\right], \mathbf{B}=\left[\begin{array}{cc}{3} & {-2} \\ {1} & {1}\end{array}\right] \text { and } \mathbf{C}\left[\begin{array}{ll}{1} & {1} \\ {2} & {2}\end{array}\right]\), find a matrix X such that AXB = C.
Solution:
A × B = C
Pre multiply by A-1 and post multiply by B-1 we get
A-1 A × BB-1 = A-1CB-1 (i.e) X = A-1CB-1
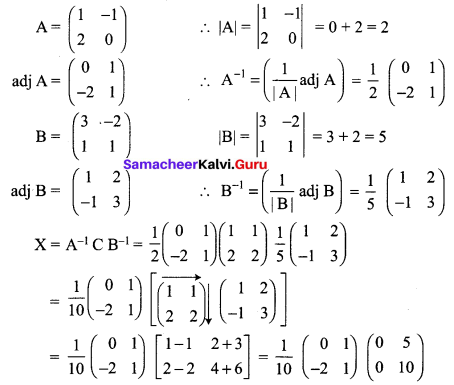
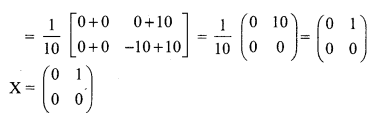
Question 14.

Solution:

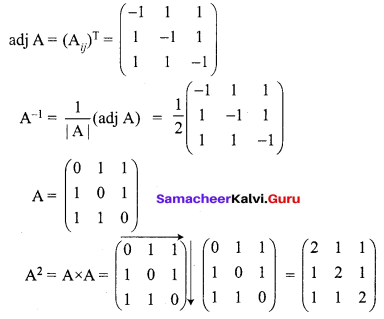

![]()
Question 15.
Decrypt the received encoded message \(\left[\begin{array}{cc}{2} & {-3}\end{array}\right]\left[\begin{array}{ll}{20} & {4}\end{array}\right]\) with the encryption matrix \(\left[\begin{array}{cc}{-1} & {-1} \\ {2} & {1}\end{array}\right]\) and the decryption matrix as its inverse, where the system of codes are described by the numbers 1-26 to the letters A- Z respectively, and the number 0 to a blank space.
Solution:
Let the encoding matrix be \(\left[\begin{array}{cc}{-1} & {-1} \\ {2} & {1}\end{array}\right]\)
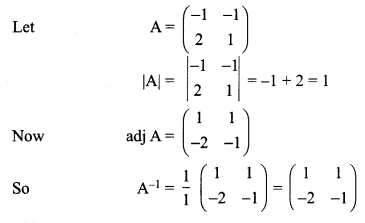
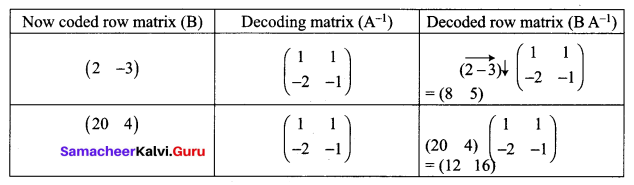
So the sequence of decoded matrices is [8 5], [12 16].
Thus the receivers read this message as HELP.
Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.1 Additional Problems
Question 1.
Using elementary transformations find the inverse of the following matrix 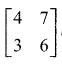
Solution:

Question 2.
Using elementary transformations find the inverse of the matrix 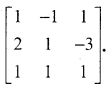
Solution:

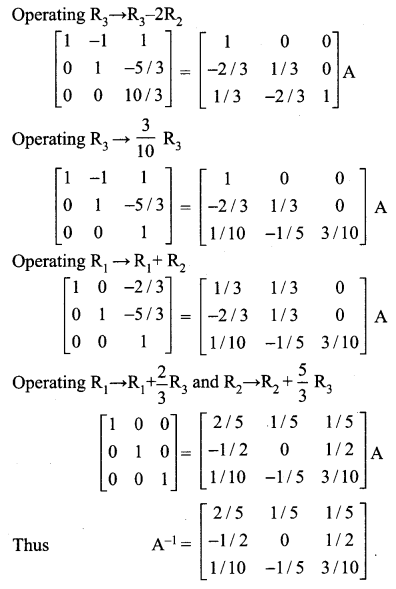
![]()
Question 3.
Using elementary transformation find the inverse of the matrix 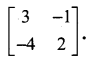
Solution:

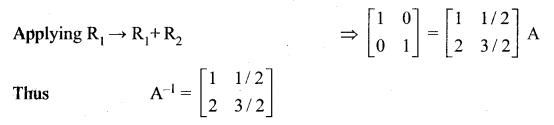
Question 4.
Using elementary transformations find the inverse of the matrix 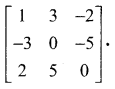
Solution:


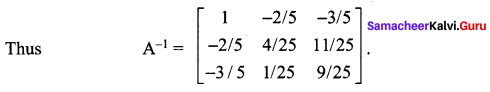
Question 5.
Using elementary transformation, find the inverse of the following matrix 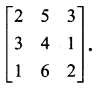
Solution:


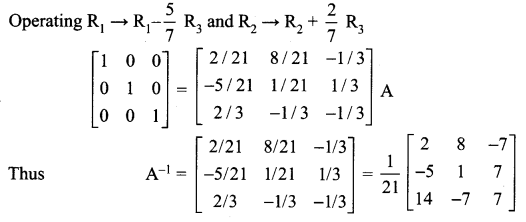
Question 6.

Solution:

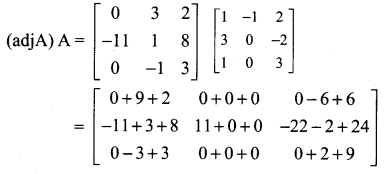
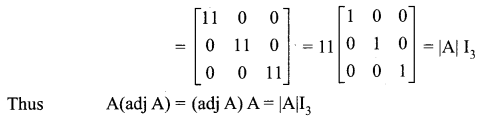
Question 7.
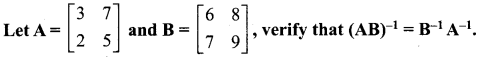
Solution:


![]()
Question 8.
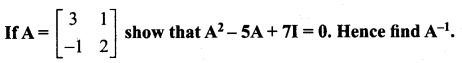
Solution:
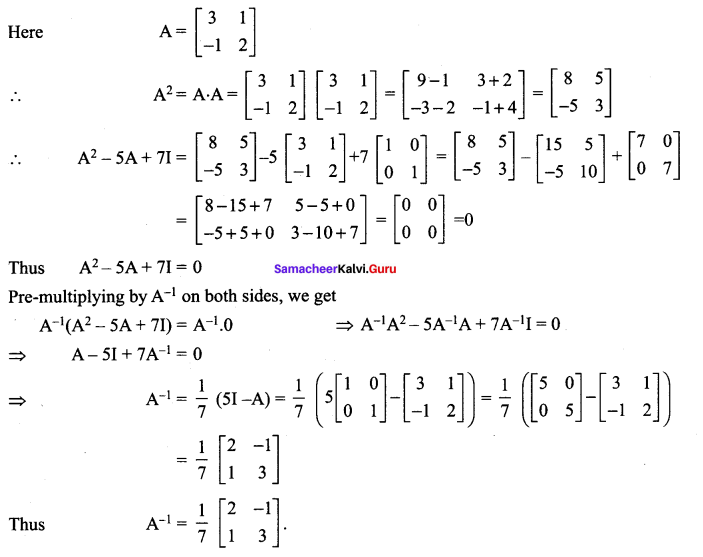
Question 9.
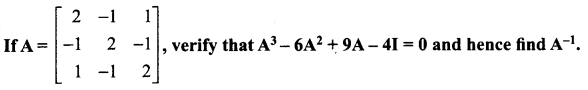
Solution:
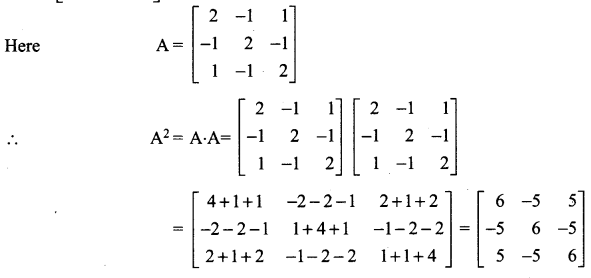


![]()
Question 10.
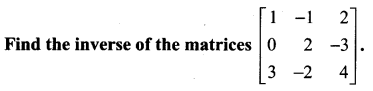
Solution:
