Samacheer Kalvi 12th Business Maths Solutions Chapter 5 Numerical Methods Ex 5.1

Students can download 12th Business Maths Chapter 5 Numerical Methods Ex 5.1 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 5 Numerical Methods Ex 5.1

Question 1.
Evaluate (log ax)
Solution:

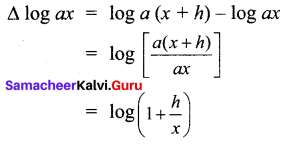
Question 2.
If y = x³ – x² + x – 1 calculate the values of y for x = 0, 1, 2, 3, 4, 5 and form the forward differences table.
Solution:
Given y = x³ – x² + x – 1
When
x = 0, y = 0 – 0 + 0 – 1 = -1
x = 1, y = 1 – 1 + 1 – 1 = 0
x = 2, y = 8 – 4 + 2 – 1 = 5
x = 3, y = 27 – 9 + 3 – 1 = 20
x = 4, y = 64 – 16 + 4 – 1 = 51
x = 5, y = 125 – 25 + 5 – 1 = 104

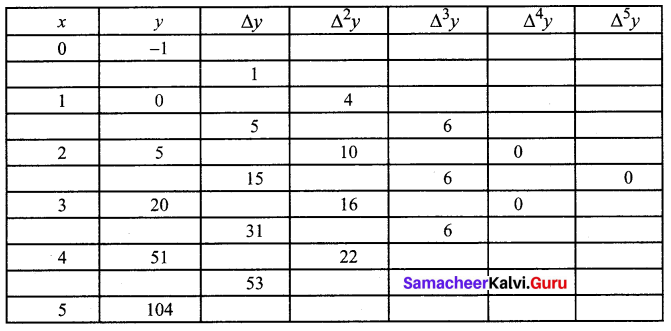
Question 3.
If h = 1 then prove that (E-1 ∆) x³ = 3x² – 3x + 1.
Solution:
Given h = 1
(E^-1 Δ)x³ = Vx³
= f(x) – f (x – h)
= f(x) – f(x – 1)
= x³ – (x – 1)³
= x³ – [x³ – 3x² + 3x – 1]
= x³ – x³ + 3x² – 3x + 1
= 3x² – 3x + 1
Hence proved

Question 4.
If f(x) = x² + 3x then show that ∆f(x) = 2x + 4
Solution:
f(x) = x² + 3 x
∆f(x) = f(x + h) – f(x)
= (x + h)² + 3(x + h) – x² – 3x
= x² + 2xh + h² + 3x + 3h – x² – 3x
= 2xh + 3h + h²
Put h = 1, ∆f(x) = 2x + 4

Question 5.
Evaluate \(\Delta\left[\frac{1}{(x+1)(x+2)}\right]\) by taking ‘1’ as the interval of differencing.
Solution:

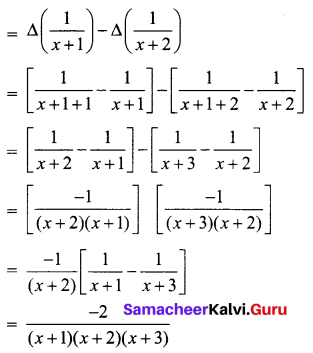
Question 6.
Find the missing entry in the following table

Solution:
Since only four values of y are given, the polynomial which fits the data is of degree three. Hence fourth differences are zeros.

Question 7.
Following are the population of a district

Find the population of the year 1911?
Solution:
Since five values are given, the polynomial which fits the data is of degree four.

From the given table
y₀ = 363, y₁ = 391, y₂ = 421, y₄ = 467 and y₅ = 501
501 – 5(467) + 10y₃ – 10(421) + 5(391) – 363 = 0
501 – 2335 + 10y₃ – 4210 + 1955 – 363 = 0
-501 + 2335 + 4210 – 1955 + 363 = 10y₃
10y₃ = 4452
y₃ = 445.2
Hence the population of the year 1911 is 445 thousand

Question 8.
Find the missing entries from the following.

Solution:
Since only four values of f(x) are given, the polynomial which fits the data is of degree three. Hence fourth differences are zeros.
Solution: