Students can download 12th Business Maths Chapter 1 Applications of Matrices and Determinants Ex 1.2 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.2
Question 1.
Solve the following equations by using Cramer’s rule
(i) 2x + 3y = 7; 3x + 5y = 9
(ii) 5x + 3y = 17; 3x + 7y = 31
(iii) 2x + y – z = 3, x + y + z = 1, x – 2y – 3z = 4
(iv) x + y + z = 6, 2x + 3y – z = 5, 6x – 2y – 3z = -7
(v) x + 4y + 3z = 2, 2x – 6y + 6z = -3, 5x – 2y + 3z = -5
Solution:
(i) 2x + 3y = 7; 3x + 5y = 9






Question 2.
A commodity was produced by using 3 units of labour and 2 units of capital, the total cost is ₹ 62. If the commodity had been produced by using 4 units of labour and one unit of capital, the cost is ₹ 56. What is the cost per unit of labour and capital? (Use determinant method).
Solution:
Let the cost per unit of labour be ₹ x and cost per unit of capital be ₹ y.


Question 3.
A total of ₹ 8,600 was invested in two accounts. One account earned 4\(\frac{3}{4}\)% annual interest and the other earned 6\(\frac{1}{2}\)% annual interest. If the total interest for one year was ₹431.25, how much was invested in each account? (Use determinant method).
Solution:
Let ₹ x and ₹ y be the amounts invested in the two accounts.


Question 4.
At marina two types of games viz., Horse riding and Quad Bikes riding are available on hourly rent. Keren and Benita spent ₹ 780 and ₹ 560 during the month of May.

Find the hourly charges for the two games (rides). (Use determinant method).
Solution:
Let hourly charges for horse riding be ₹ x and hourly charges for Quad bike riding be ₹ y.
According to the problem, for Keren, we have 3x + 4y as total amount and for Benita, we have 2x + 3y as the total amount.
That is 3x + 4y = 780
2x + 3y = 560

Hence hourly charges for horse riding and bike riding are ₹ 100 and ₹ 120 respectively.
Question 5.
In a market survey three commodities A, B and C were considered. In finding out the index number some fixed weights were assigned to the three varieties in each of the commodities. The table below provides information regarding the consumption of three commodities according to the three varieties and also the total weight received by the commodity.
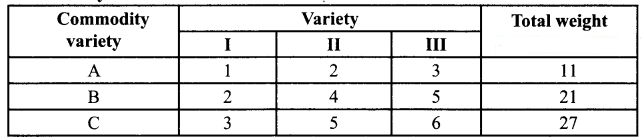
Find the weights assigned to the three varieties by using Cramer’s Rule.
Solution:
Let the weights assigned to the three varieties be x, y and z respectively.
According to the problem,
For variety A, x + 2y + 3z = 11
For variety B, 2x + 4y + 5z = 21
For variety C, 3x + 5y + 6z = 27

Hence the weights assigned to the three varieties are 2, 3 and 1 units respectively.
Question 6.
A total of ₹ 8,500 was invested in three interest-earning accounts. The interest rates were 2%, 3% and 6% if the total simple interest for one year was ₹ 380 and the amount invested at 6% was equal to the sum of the amounts in the other two accounts, then how much was invested in each account? (use Cramer’s rule).
Solution:
Let the amounts invested in the three accounts be Rs. x, Rs. y and Rs. z
Interest for the three accounts are \(\frac{2}{100}\)x, \(\frac{3}{100}\)y and \(\frac{6}{100}\)z
According to the problem, x + y + z = 8500 ……. (1)
\(\frac{2}{100} x+\frac{3}{100} y+\frac{6}{100} z=380\)
(or) multiplying by 100,
2x + 3y + 6z = 38000 ……… (2)
z = x + y or x + y – z = 0 ………. (3)
