Students can download 12th Business Maths Chapter 1 Applications of Matrices and Determinants Ex 1.1 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.1
Question 1.
Find the rank of each of the following matrices.
Solution:
(i) Let A = \(\left(\begin{array}{ll}
5 & 6 \\
7 & 8
\end{array}\right)\)
Order of A is 2 × 2.
ρ(A) ≤ 2
Consider the second order minor
\(\left|\begin{array}{ll}
5 & 6 \\
7 & 8
\end{array}\right|\) = 40 – 42 = -2 ≠ 0
There is a minor of order 2, which is not zero.
ρ(A) = 2
(ii) Let A = \(\left(\begin{array}{ll}
1 & -1 \\
3 & -6
\end{array}\right)\)
Order of A is 2 × 2
ρ(A) ≤ 2
Consider the second order minor
\(\left|\begin{array}{ll}
1 & -1 \\
3 & -6
\end{array}\right|\) = -6 + 3 = -3 ≠ 0
ρ(A) = 2
(iii) Let A = \(\left(\begin{array}{ll}
1 & 4 \\
2 & 8
\end{array}\right)\)
Since A is of order 2 × 2, ρ(A) ≤ 2
Now \(\left|\begin{array}{ll}
1 & 4 \\
2 & 8
\end{array}\right|\) = 8 – 8 = 0
Since second order minor vanishes ρ(A) ≠ 2
But first order minors, |1|, |4|, |2|, |8| are non zero.
ρ(A) = 1
(iv) Let A = \(\left(\begin{array}{ccc}
2 & -1 & 1 \\
3 & 1 & -5 \\
1 & 1 & 1
\end{array}\right)\)
Order of A is 3 × 3
ρ(A) ≤ 3
Consider the third order minor
\(\left|\begin{array}{ccc}
2 & -1 & 1 \\
3 & 1 & -5 \\
1 & 1 & 1
\end{array}\right|\)
= 2(1 + 5) + 1 (3 + 5) + 1(3 – 1)
= 2(6) + 8 + 2
= 22 ≠ 0
There is a minor of order 3, which is non zero.
ρ(A) = 3
(v) Let A = \(\left(\begin{array}{ccc}
-1 & 2 & -2 \\
4 & -3 & 4 \\
-2 & 4 & -4
\end{array}\right)\)
Since order of A is 3 × 3, ρ(A) ≤ 3
Now,
\(\left|\begin{array}{ccc}
-1 & 2 & -2 \\
4 & -3 & 4 \\
-2 & 4 & -4
\end{array}\right|\)
= -1(12 – 16) -2(-16 + 8) – 2(16 – 6)
= 4 + 16 – 20
= 0
Since the third order minor vanishes, ρ(A) ≠ 3
Consider \(\left|\begin{array}{cc}
-1 & 2 \\
4 & -3
\end{array}\right|\) = 3 – 8 = -5 ≠ 0
There is a minor order 2, which is not zero
ρ(A) = 2
(vi) Let A = \(\left(\begin{array}{cccc}
1 & 2 & -1 & 3 \\
2 & 4 & 1 & -2 \\
3 & 6 & 3 & -7
\end{array}\right)\)
Let us transform the matrix A to an echelon form by using elementary transformations.




Question 2.
If A = \(\left(\begin{array}{ccc}
1 & 1 & -1 \\
2 & -3 & 4 \\
3 & -2 & 3
\end{array}\right)\) and B = \(\left(\begin{array}{ccc}
1 & -2 & 3 \\
-2 & 4 & -6 \\
5 & 1 & -1
\end{array}\right)\), then find the rank of AB and the rank of BA.
Solution:
Given A = \(\left(\begin{array}{ccc}
1 & 1 & -1 \\
2 & -3 & 4 \\
3 & -2 & 3
\end{array}\right)\) and B = \(\left(\begin{array}{ccc}
1 & -2 & 3 \\
-2 & 4 & -6 \\
5 & 1 & -1
\end{array}\right)\)


Question 3.
Solve the following system of equations by rank method.
x + y + z = 9, 2x + 5y + 7z = 52, 2x + y – z = 0
Solution:
The given equations are x + y + z = 9, 2x + 5y + 7z = 52, 2x + y – z = 0
The matrix equation corresponding to the given system is
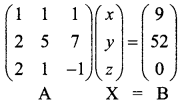

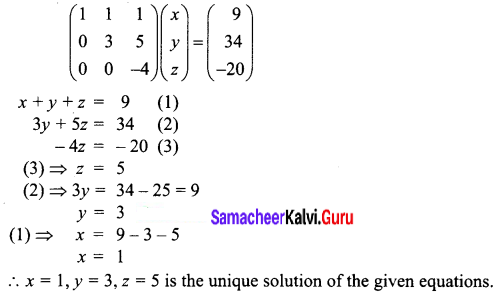
Question 4.
Show that the equations 5x + 3y + 7z = 4, 3x + 26y + 2z = 9, 7x + 2y + 10z = 5 are consistent and solve them by rank method.
Solution:
The given equations are,
5x + 3y + 7 = 4
3x + 26y + 2z = 9
7x + 2y + 10z = 5
The matrix equation corresponding to the given system is
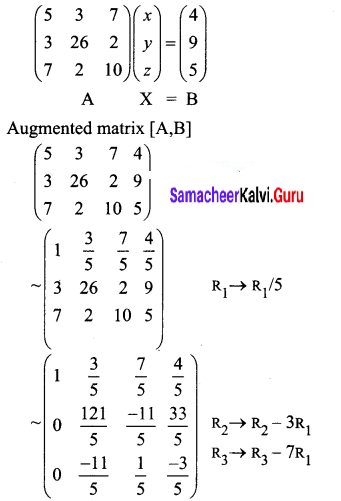


Question 5.
Show that the following system of equations have unique solution:
x + y + z = 3, x + 2y + 3z = 4, x + 4y + 9z = 6 by rank method.
Solution:
The given system of equations can be written in matrix equation,

The last matrix is in echelon form. It has 3 non – zero rows,
ρ(A) = ρ([A, B]) = 3 = number of unknowns.
The given system is consistent and has a unique solution.
To find the solution, we write the echelon form into matrix form.
\(\left(\begin{array}{lll}
1 & 1 & 1 \\
0 & 1 & 2 \\
0 & 0 & 2
\end{array}\right)\left(\begin{array}{l}
x \\
y \\
z
\end{array}\right)=\left(\begin{array}{l}
3 \\
1 \\
0
\end{array}\right)\)
x + y + z = 3 …… (1)
y + 2z = 1 …… (2)
2z = 0 …… (3)
(3) ⇒ z = 0
(2) ⇒ y = 1
(1) ⇒ x = 2
So the unique solution is x = 2, y = 1, z = 0
Question 6.
For what values of the parameter X, will the following equations fail to have unique solution: 3x – y + λz = 1, 2x + y + z = 2, x + 2y – λz = -1 by rank method.
Solution:
The given system can be written in matrix equation form as given below:
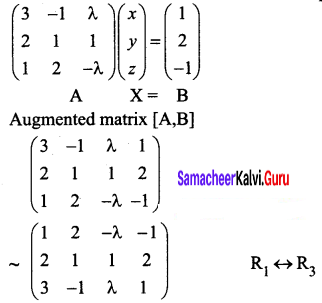

λ = \(\frac{-7}{2}\)
So when λ = \(\frac{-7}{2}\), the equations fail to have unique solution.
Note: The system cannot have an infinite number of solutions, since ρ([A, B]) = 3 = a number of unknowns.
Question 7.
The price of three commodities, X,Y and Z are and z respectively Mr. Anand purchases 6 units of Z and sells 2 units of X and 3 units of Y. Mr.Amar purchases a unit of Y and sells 3 units of X and 2 units of Z. Mr. Amit purchases a unit of X and sells 3 units of Y and a unit of Z. In the process they earn ₹ 5,000/-, ₹2,000/- and ₹ 5,500/- respectively. Find the prices per unit of three commodities by rank method.
Solution:
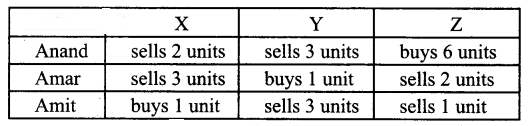
The price of three commodities X, Y, Z are given as x, y, z.
We form the following system of equations from the given conditions.
Anand → 2x + 3y – 6z = 5000
Amar → 3x – y + 2z = 2000
Amit → -x + 3y + z = 5500
The matrix equation is given by



The prices per unit of the three commodities are Rs.1000, Rs.2000 and Rs.500
Question 8.
An amount of ₹ 5,000/- is to be deposited in three different bonds bearing 6%, 7% and 8% per year respectively. Total annual income is ₹ 358/-. If the income from the first two investments is ₹ 70/- more than the income from the third, then find the amount of investment in each bond by the rank method.
Solution:
Let the amount of investment in the three different bonds be Rs. x, Rs. y and Rs. z respectively.
We get the following equations according to the given conditions,
x + y + z = 5000


The above equivalent matrix is in echelon form with 3 non-zero rows.
So ρ(A) = ρ([A, B]) = 3 = number of unknowns.
the system has a unique solution.
The matrix equation is given by
\(\left(\begin{array}{ccc}
1 & 1 & 1 \\
0 & 1 & 2 \\
0 & 0 & -16
\end{array}\right)\left(\begin{array}{l}
x \\
y \\
z
\end{array}\right)=\left(\begin{array}{c}
5000 \\
5800 \\
-28800
\end{array}\right)\)
x + y + z = 5000 …(1)
y + 2z = 5800 …(2)
-16z = -28800 …(3)
(3) ⇒ z = 1800
(2) ⇒ y = 5800 – 2(1800) = 2200
(1) ⇒ x = 5000 – 2200 – 1800 = 1000
The amount invested in the three bonds are ₹ 1000, ₹ 2200 and ₹ 1800.