Samacheer Kalvi 12th Business Maths Solutions Chapter 1 Applications of Matrices and Determinants Additional Problems

Students can download 12th Business Maths Chapter 1 Applications of Matrices and Determinants Additional Problems Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 1 Applications of Matrices and Determinants Additional Problems

I. One Mark Questions

Choose the correct statement.

Question 1.
If A is a matrix of order m × n, then ______
(a) ρ(A) = m
(b) ρ(A) = n
(c) ρ(A) = min of {m, n}
(d) ρ(A) < m
Answer:
(c) ρ(A) = min of {m, n}

Question 2.
If 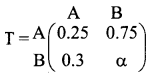 is a transition probability matrix, then the value of a is
(a) 0.5
(b) 0.7
(c) 0
(d) 0.6
Answer:
(b) 0.7
Hint:
0.3 + α = 1
⇒ α = 1 – 0.3 = 0.7

Question 3.
Let AX = B is a system of n non-homogeneous linear equation. Then which of the following is correct.
(a) |A|= 0
(b) A = B
(c) |A| ≠ 0
(d) ρ(A) < n
Answer:
(c) |A| ≠ 0

Question 4.
Choose the incorrect pair.

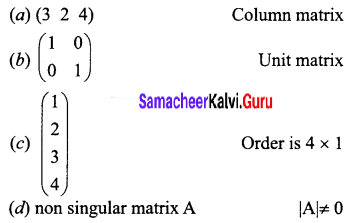
Answer:
(a) (3 2 4) – Column matrix

Question 5.
If A is matrix [A, B] is the augmented matrix then which of the following is true?
(a) ρ([A, B]) = ρ(A)
(b) ρ([A, B]) ≥ ρ(A)
(c) ρ([A, B]) = ρ(A) > n
(d) ρ([A, B]) < ρ(A)
Answer:
(b) ρ([A, B]) ≥ ρ(A)

Question 6.
Choose the echelon matrix.
(a) \(\left[\begin{array}{ll}
0 & 1 \\
1 & 0 \\
0 & 0
\end{array}\right]\)
(b) \(\left[\begin{array}{ll}
1 & 2 \\
0 & 1 \\
0 & 0
\end{array}\right]\)
(c) \(\left[\begin{array}{ll}
1 & 2 \\
0 & 1 \\
0 & 1
\end{array}\right]\)
(d) \(\left[\begin{array}{ll}
1 & 0 \\
0 & 0 \\
0 & 1
\end{array}\right]\)
Answer:
(b) \(\left[\begin{array}{ll}
1 & 2 \\
0 & 1 \\
0 & 0
\end{array}\right]\)

Question 7.
Let A be a non-singular matrix of order (3 × 3). Then |adj A| is equal to _______
(a) |A|
(b) |A|²
(c) |A|³
(d) 3|A|
Answer:
(b) |A|²

Question 8.
For what value of k does the matrix. A = \(\left[\begin{array}{cc}
k & -1 \\
3 & 2
\end{array}\right]\) does not have inverse?
(a) 1
(b) \(\frac{-3}{2}\)
(c) 0
(d) -1
Answer:
(b) \(\frac{-3}{2}\)
Hint:

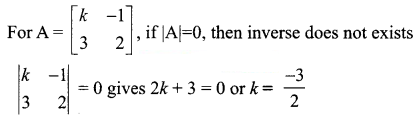
Question 9.
Rank of the matrix A = \(\left(\begin{array}{rrrr}
1 & -1 & 2 & 0 \\
0 & 2 & 0 & 3
\end{array}\right)\) is _______
(a) 1
(b) 0
(c) 2
(d) -1
Answer:
(c) 2
Hint:
The second order minors, \(\left|\begin{array}{cc}
1 & -1 \\
0 & 2
\end{array}\right|,\left|\begin{array}{cc}
-1 & 2 \\
2 & 0
\end{array}\right|,\left|\begin{array}{cc}
2 & 0 \\
0 & 3
\end{array}\right|\) are not zero. So rank is 2

Question 10.
Choose the correct answer.
(a) A system of the linear equation always has a unique solution.
(b) A system of the linear equation can have more than one solution.
(c) A system of the linear equation need not be consistent.
(d) All of the above
Answer:
(d) All of the above

Question 11.
For the matrix equation \(\left(\begin{array}{cc}
1 & 2 \\
3 & -1
\end{array}\right)\left(\begin{array}{l}
x \\
y
\end{array}\right)=\left(\begin{array}{l}
7 \\
3
\end{array}\right)\) the augmented matrix is _______
(a) \(\left(\begin{array}{ccc}
1 & 2 & 7 \\
3 & -1 & 3
\end{array}\right)\)
(b) \(\left(\begin{array}{ll}
1 & 7 \\
3 & 3
\end{array}\right)\)
(c) \(\left(\begin{array}{ll}
7 & 1 \\
3 & 3
\end{array}\right)\)
(d) \(\left(\begin{array}{rrr}
1 & 7 & 2 \\
3 & 3 & -1
\end{array}\right)\)
Answer:
(a) \(\left(\begin{array}{ccc}
1 & 2 & 7 \\
3 & -1 & 3
\end{array}\right)\)

Question 12.
Find the correct statement. Cramer’s rule can be used to solve, _______
(a) n equations in n unknowns
(b) When determinant of the coefficient matrix is non-zero.
(c) The number of unknowns need not be equal to a number of equations.
(d) For infinite solutions
Answer:
(a) n equations in n unknowns & (b) When determinant of the coefficient matrix is non-zero.

Question 13.
Which of the following is a transition probability matrix?
(a) \(\left(\begin{array}{cc}
0.3 & 0.6 \\
0.15 & 0.85
\end{array}\right)\)
(b) \(\left(\begin{array}{ccc}
0.9 & 0.075 & 0.025 \\
0.15 & 0.8 & 0.05 \\
0.25 & 0.25 & 0.5
\end{array}\right)\)
(c) \(\left(\begin{array}{ll}
1 & 0.2 \\
0.3 & 0.25
\end{array}\right)\)
(d) \(\left(\begin{array}{cc}
0.35 & 0.6 \\
0.2 & 0.7
\end{array}\right)\)
(i) only a
(ii) only b
(iii) both c and d
(iv) both a and b
Answer:
(iv) both a and b
Hint:
Sum of all the probabilities should be equal to one

Question 14.
Choose the correct statements.
(a) the rank of an identity matrix is zero.
(b) the rank of an adjoint matrix is more than the rank of a matrix
(c) the rank of a diagonal matrix is equal to the number of rows
(d) the rank of an echelon matrix is greater than the matrix
Answer:
(c) the rank of a diagonal matrix is equal to the number of rows

Question 15.

Answer:
1 – d, 2 – c, 3 – a, 4 – b

II. 2 Mark Questions

Question 1.
Show that the inverse of A = \(\left(\begin{array}{cc}
-6 & 9 \\
4 & -6
\end{array}\right)\) does not exist
Solution:
Show |A| = 0

Question 2.
Find the rank of A = \(\left(\begin{array}{lll}
1 & 2 & 3 \\
2 & 3 & 4 \\
3 & 5 & 7
\end{array}\right)\)
Solution:
Given A = \(\left(\begin{array}{lll}
1 & 2 & 3 \\
2 & 3 & 4 \\
3 & 5 & 7
\end{array}\right)\)
Consider \(\left(\begin{array}{lll}
1 & 2 & 3 \\
2 & 3 & 4 \\
3 & 5 & 7
\end{array}\right)\)
= 1(21 – 20) – 2(14 – 12) + 3(10 – 9)
= 1 – 4 + 3
= 0
Since third order minor equals zero, ρ(A) < 3
Consider \(\left|\begin{array}{ll}
1 & 2 \\
2 & 3
\end{array}\right|\) = 3 – 4 = -1 ≠ 0
There is a minor of order 2 which is not zero. Hence ρ(A) = 2

Question 3.
Find the rank of A = \(\left[\begin{array}{rrrr}
4 & 5 & -6 & -1 \\
7 & -3 & 0 & 8
\end{array}\right]\)
Solution:
Given A = \(\left[\begin{array}{rrrr}
4 & 5 & -6 & -1 \\
7 & -3 & 0 & 8
\end{array}\right]\)
Consider the minor \(\left|\begin{array}{cc}
5 & -6 \\
-3 & 0
\end{array}\right|=-18 \neq 0\)
Since a minor of order 2 is not zero, rank is 2

Question 4.
Solve the system by Cramer’s rule, 4x – 3y = 11; 6x + 5y = 7
Solution:
4x – 3y = 11; 6x + 5y = 7

Question 5.
Solve the system by rank method.
3x + 5y = -7; x + 4y = -14
Solution:
3x + 5y = -7; x + 4y = -14
The matrix equation of the system is

Number of non-zero rows is 2
So ρ(A) = ρ([A, B]) = 2
Now the new matrix equation is
-7y = 35 ⇒ y = -5
x + 4y = -14 ⇒ x = -14 – 4(-5) = 6
Solution is (6, -5)

Question 6.
Find the solution of the system 5x + y = -13; 3x – 2y = 0
Solution:
5x + y = -13; 3x – 2y = 0
We solve the system by Cramer’s rule

III. 3 and 5 Mark Questions

Question 1.
Find λ so that the matrix \(\left(\begin{array}{ccc}
8 & 9 & 7 \\
7 & 8 & 6 \\
9 & 10 & \lambda
\end{array}\right)\) is a singular matrix.
Solution:

Question 2.
Find k so that the matrix \(\left(\begin{array}{ccc}
1 & 2 & k \\
3 & 4 & 5 \\
7 & 10 & 12
\end{array}\right)\) is a non-singular matrix.
Solution:

Question 3.
Solve by Cramer’ rule, x – y + z = 2; 2x – y = 0; 2y – z = 1
Solution:
x – y + z = 2; 2x – y = 0; 2y – z = 1
The matrix equation corresponding to the system is

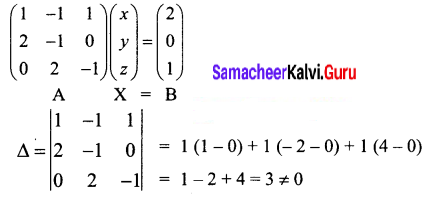
Question 4.
Solve by rank method x + 2y – 3z = -4; 2x + 3y + 2z = 2; 3x – 3y – 4z = 11
Solution:
x + 2y – 3z = -4; 2x + 3y + 2z = 2; 3x – 3y – 4z = 11
The matrix equation is

The last equivalent matrix is in echelon form.
ρ(A) = ρ([A, B]) = 3 = Number of unknowns
The new matrix equation is given by \(\left(\begin{array}{ccc}
1 & 2 & -3 \\
0 & -1 & 8 \\
0 & 0 & -67
\end{array}\right)\left(\begin{array}{l}
x \\
y \\
z
\end{array}\right)=\left(\begin{array}{c}
-4 \\
10 \\
-67
\end{array}\right)\)
x + 2y – 3z = -4 ……. (1)
-y + 8z = 10 …….. (2)
-67z = -67 ……… (3)
(3) ⇒ z = 1
(2) ⇒ -y + 8 = 10 ⇒ -y = 2 ⇒ y = -2
(1) ⇒ x = -4 -2(-2) + 3(1) ⇒ x = 3
Hence the solution is (x, y, z) = (3, -2, 1)

Question 5.
The sum of three numbers is 20. If we multiply the first by 2 and add the second number and subtract the third we get 23. If we multiply the first by 3 and add second and third to it, we get 46. By using rank method find the numbers.
Solution:
Let the three number be x, y and z respectively.
According to the problem,
x + y + z = 20
2x + y – z = 23
3x + y + z = 46
The matrix equation is given by

x + y + z = 20 …….. (1)
-y – 3z = -17 …….. (2)
4z = 20 …….. (3)
(3) ⇒ z = 5
(2) ⇒ -y = -17 + 3(5) = -2 ⇒ y = 2
(1) ⇒ x = 20 – 2 – 5 = 13
Hence the three numbers are (13, 2, 5)

Question 6.
Weekly expenditure in an office for three weeks is given as follows. Calculate the salary for each type of staff using Cramer’s rule.

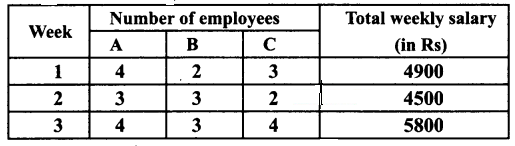
Solution:
Let the salary for the three types of staff A, B and C be ₹ x, ₹ y and ₹ z respectively.
According to the problem we have,
4x + 2y + 3z = 4900
3x + 3y + 2z = 4500
4x + 3y + 4z = 5800

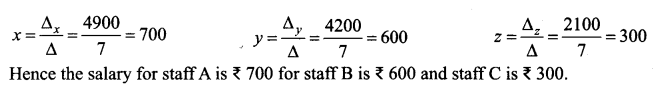
Question 7.
Show that the equations x – 3y – 8z = -10; 3x + y – 4z = 0; 2x + 5y + 6z = 13 are consistent and have infinite sets of solution.
Solution:

The last equivalent matrix is in echelon form. It has two non-zero rows.
ρ(A) = ρ([A, B]) = 2 < number of unknowns
The system is consistent and has infinitely many solutions
The changed matrix equation is given by \(\left(\begin{array}{ccc}
1 & -3 & -8 \\
0 & 1 & 2 \\
0 & 0 & 0
\end{array}\right)\left(\begin{array}{c}
x \\
y \\
z
\end{array}\right)=\left(\begin{array}{c}
-10 \\
3 \\
0
\end{array}\right)\)
x – 3y – 8z = -10 ……. (1)
y + 2z = 3 ……. (2)
(2) ⇒ y = 3 – 2z
(1) ⇒ x = -10 + 3y + 8z
⇒ x = -10 + 3(3 – 2z) + 8z
⇒ x = -10 + 9 – 6z + 8z
⇒ x = 2z – 1
Let us take z = k, k ∈ R. We get y = 3 – 2k and x = 2k – 1.
By giving diffemet values for k, we get different solutions.

Question 8.
Find the rank of the matrix by reducing to echelon form A = \(\left(\begin{array}{cccc}
1 & 1 & 1 & 1 \\
1 & 3 & -2 & 1 \\
2 & 0 & -3 & 2
\end{array}\right)\)
Solution:

Question 9.
Show that the equations x – 3y + 4z = 3; 2x – 5y + 7z = 6; 3x – 8y + 11z = 1 are inconsistent.
Solution:
x – 3y + 4z = 3; 2x – 5y + 7z = 6; 3x – 8y + 11z = 1

The last equivalent matrix is in the echelon form. [A, B] has 3 non-zero rows and [A] has 2 non-zero rows.
ρ([A, B]) = 3; ρ(A) = 2
ρ(A) ≠ ρ([A, B])
The system is inconsistent and has no solution.

Question 10.
Find k if the equations 2x + 3y – z = 5; 3x – y + 4z = 2; x + 7y – 6z = k are consistent.
Solution:
Given that the system 2x + 3y – z = 5; 3x – y + 4z = 2, x + 7y – 6z = k is consistent.

ρ(A) = 2 ρ([A, B]) = 2 or 3
For the equations to be consistent, ρ([A, B]) = ρ(A) = 2
-8 + k = 0 ⇒ k = 8

Question 11.
Find k if the equations x + y + z = 3; x + 3y + 2z = 6; x + 5y + 3z = k are inconsistent.
Solution:
Given that the system is inconsistent


For the equations to be inconsistent, ρ[(A, B)] ≠ ρ(A)
Here ρ(A) = 2 So ρ([A, B]) ≠ 2
That is the last row of the echelon matrix should not be zero
⇒ k ≠ 9

Question 12.
Two newspapers A and B are published in a city. Their present market shares are 15% for A and 85% for B. Of those who bought A the previous year, 65% continue to buy it again while 35% switch over to B. Of those who bought B the previous year, 55% buy it again and 45% switch over to A. Find their market shares after two years.
Solution:
Let the present shares of A and B be denoted by (0.15 0.85)
The transition probability matrix is given by

Hence their market shares after 2 years will be 0.546 × 100 = 54.6 % and 0.454 × 100 = 45.4%

Question 13.
The pattern of sunny and rainy days on a planet has two states. Every sunny day is followed by another sunny day with probability 0.8. Every rainy day is followed by another rainy day with probability 0.6. Today is sunny on the planet. What is the chance of rain the day after tomorrow?
Solution:
Let S and R denote sunny and rainy days on the planet
The transition probability matrix is given by

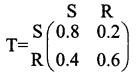
We have to find the probability of rain after two days. We have to find T²

Hence if today is sunny on the planet, the chance of rain the day after tomorrow is 0.28.