Students can Download Physics Chapter 10 Oscillations, Questions and Answers, Notes Pdf, Samacheer Kalvi 11th Physics Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Physics Solutions Chapter 10 Oscillations
Samacheer Kalvi 11th Physics Oscillations Textual Evaluation Solved
Samacheer Kalvi 11th Physics Oscillations Multiple Choice Questions
Question 1.
In a simple harmonic oscillation, the acceleration against displacement for one complete oscillation will be [model NSEP 2000-01 ]
(a) an ellipse
(b) a circle
(c) a parabola
(d) a straight line
Answer:
(d) a straight line
Question 2.
A particle executing SHM crosses points A and B with the same velocity. Having taken 3 s in passing from A to B, it returns to B after another 3s. The time period is
(a) 15s
(b) 6s
(c) 12s
(d) 9s
Answer:
(c) 12s
Hint:
Time period of Oscillation = 2 × (time taken to go from A to B + the next time taken to return at B)
= 2 × (3 + 3)
= 2 × 6
Time period = 12s
Question 3.
The length of a second’s pendulum on the surface of the Earth is 0.9 m. The length of the same pendulum on surface of planet X such that the acceleration of the planet X is n times greater than the Earth
(a) 0.9 n
(b) \(\frac{0.9}{n} \mathrm{m}\)
(c) 0.9 n2m
(d) \(\frac{0.9}{n^{2}}\)
Answer:
(a) 0.9 n
Hint:
Second’s pendulum on the surface of planet,
Time period, T = 2 sec
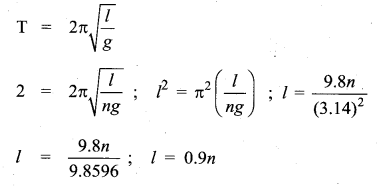
![]()
Question 4.
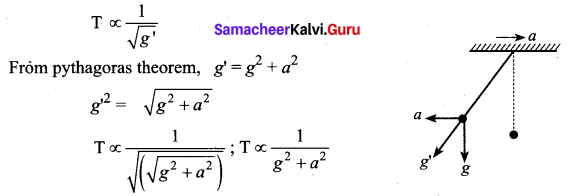
A simple pendulum is suspended from the roof of a school bus which moves in a horizontal direction with an acceleration a, then the time period is …..

Answer:
\(\mathrm{T} \propto \frac{1}{g^{2}+a^{2}}\)

Question 5.
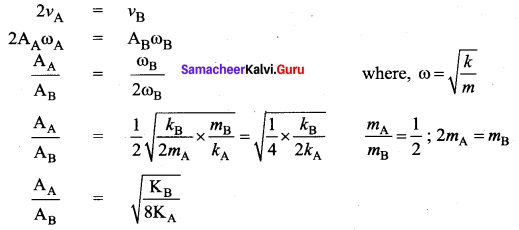
Two bodies A and B whose masses are in the ratio 1:2 are suspended from two separate massless springs of force constants kA and kB respectively. If the two bodies oscillate vertically such that their maximum velocities are in the ratio 1 : 2, the ratio of the amplitude A to that of B is
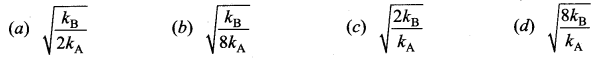
Answer:
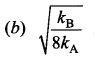
Hint:
The maximum velocity in the Oscillation is given as vmax = Aω
The ratio of maximum velocity, vA: vB = 1 : 2
Question 6.
A spring is connected to a mass m suspended from it and its time period for vertical oscillation is T. The spring is now cut into two equal halves and the same mass is suspended from one of the halves. The period of vertical oscillation is

Answer:
(b) \(\mathrm{T}^{\prime}=\frac{\mathrm{T}}{\sqrt{2}}\)
Hint:
Spring constant of spring depends upon number of coil in the spring! When you cut the spring then the number of coil remain half of the original, so
k’ = 2k
Hint:
According to law of accelaration, the time period of simple pendulum
Question 5.
Two bodies A and B whose masses are in the ratio 1 : 2 are suspended from two separate massless springs of force constants kA and kB respectively. If the two bodies oscillate vertically such that their maximum velocities are in the ratio 1 : 2, the ratio of the amplitude A to that of B is

Answer:
(b) \(\sqrt{\frac{k_{\mathrm{B}}}{8 k_{\mathrm{A}}}}\)
Hint:
The maximum velocity in the Oscillation is given as vmax = Aω
The ratio of maximum velocity, vA : vB = 1 : 2

Question 6.
A spring is connected to a mass m suspended from it and its time period for vertical oscillation is T. The spring is now cut into two equal halves and the same mass is suspended from one of the halves. The period of vertical oscillation is

Answer:
(b) \(\mathrm{T}^{\prime}=\frac{\mathrm{T}}{\sqrt{2}}\)
Hint:
Spring constant of spring depends upon number of coil in the spring! When you cut the spring then the number of coil remain half of the original, so
k’ = 2k
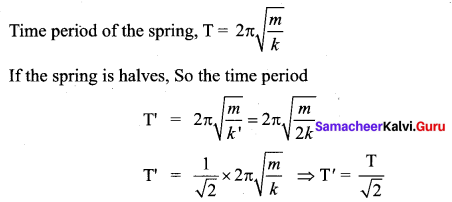
Question 7.
The time period for small vertical oscillations of block of mass m when the masses of the pulleys are negligible and spring constant k1 and k2 is ….

Answer:
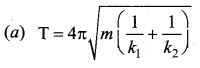
Question 8.
A simple pendulum has a time period T1. When its point of suspension is moved vertically upwards according as y = kt2, where y is vertical distance covered and k = 1 ms-2, its time period becomes T2. Then 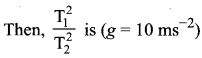 [IIT 2005]
[IIT 2005]

Answer:
(c) \(\frac{6}{5}\)
Hint:

Question 9.
An ideal spring of spring constant k, is suspended from the ceiling of a room and a block of mass M is fastened to its lower end. If the block is released when the spring is un-stretched, then the maximum extension in the spring is : [IIT 2002]

Answer:
(c) \(2 \frac{\mathrm{Mg}}{k}\)
Hint:
Work by gravity + Work by spring = Change in kinetic energy
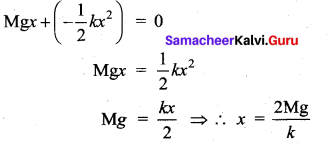
Question 10.
A pendulum is hung in a very high building oscillates to and fro motion freely like a simple harmonic oscillator. If the acceleration of the bob is 16 ms-2 at a distance of 4 m from the mean position, then the time period is [NEET 2018 model]
(a) 2s
(b) 1s
(c) 2πs
(d) πs
Answer:
(d) πs
Hint:
Acceleration, a = 16 m/s2
displacement, y = 4m
According to SHM,

Question 11.
A hollow sphere is filled with water. It is hung by a long thread. As the water flows out of a hole at the bottom, the period of oscillation will
(a) first increase and then decrease
(b) first decrease and then increase
(c) increase continuously
(d) decrease continuously
Answer:
(a) first increase and then decrease
![]()
Question 12.
The damping force on an oscillator is directly proportional to the velocity. The units of the constant of proportionality are ………
![]()
Answer:
(c) \(\mathrm{kg} \mathrm{s}^{-1}\)

Question 13.
When a damped harmonic oscillator completes 100 oscillations, its amplitude is reduced to \(\frac{1}{3}\) of its initial value. What will be its amplitude when it completes 200 oscillations?

Answer:
(d) \(\frac{1}{9}\)
Hint:
In damped vibration, amplitude at any instant t is
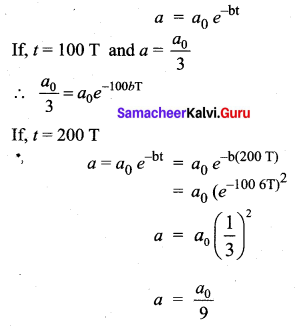
Question 14.
Which of the following differential equations represents a damped harmonic oscillator?

Answer:
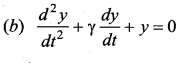
Question 15.
If the inertial mass and gravitational mass of the simple pendulum of length / are not equal, then the time period of the simple pendulum is …..
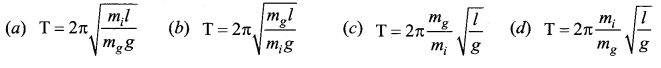
Answer:
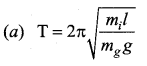
Samacheer Kalvi 11th Physics Oscillations Short Answer Questions
Question 1.
What is meant by periodic and non-periodic motion? Give any two examples, for each motion.
Answer:
Periodic motion: Any motion which repeats itself in a fixed time interval is known as periodic motion. Examples: Hands in pendulum clock, swing of a cradle.
Non-Periodic motion: Any motion which does not repeat itself after a regular interval of time is known as non-periodic motion. Example: Occurrence of Earth quake, eruption of volcano.
Question 2.
What is meant by force constant of a spring?
Answer:
The force constant (or) spring factor is defined as the restoring force produced per unit displacement.
![]()
Question 3.
Define time period of simple harmonic motion.
Answer:
Time period: The time period is defined as the time taken by a particle to complete one oscillation. It is usually denoted by T. For one complete revolution, the time taken is t = T, therefore,
![]()
Question 4.
Define frequency of simple harmonic motion.
Answer:
The number of oscillations produced by the particle per second is called frequency. It is denoted by f. SI unit for frequency is s-1 or hertz (Hz).
Mathematically, frequency is related to time period by f = \(\frac{1}{\mathrm{T}}\)
Question 5.
What is an epoch?
Answer:
The phase of a vibrating particle corresponding to time t = 0 is called initial phase or epoch. At, t = φ, φ = φ0.
The constant φ0 is called initial phase or epoch. It tells about the initial state of motion of the vibrating particle.
Question 6.
Write short notes on two springs connected in series.
Answer:
Phase: The phase of a vibrating particle at any instant completely specifies the state of the particle. It expresses the position and direction of motion of the particle at that instant with respect to its mean position the phase of the vibrating particle. At time t = 0 s (initial time), the phase φ = φ0 is called epoch (initial phase) where φ0 is called the angle of epoch.
Question 7.
Write short notes on two springs connected in parallel.
Answer:
When two or more springs are connected in parallel, we can replace (by removing) all these springs with an equivalent spring (effective spring) whose net effect is same as if all the springs are in parallel connection.
Question 8.
Write down the time period of simple pendulum.
Answer:
The angular frequency of this oscillator (natural frequency of this system) is
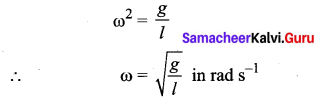
The frequency of oscillations is
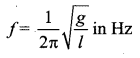
and time period of oscillations is
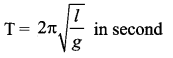
Question 9.
State the laws of simple pendulum?
Answer:
Law of length: For a given value of acceleration due to gravity, the time period of a simple pendulum is directly proportional to the square root of length of the pendulum.
![]()
Law of acceleration: For a fixed length, the time period of a simple pendulum is inversely proportional to square root of acceleration due to gravity.
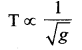
![]()
Question 10.
Write down the equation of time period for linear harmonic oscillator.
Answer:
From Newton’s second law, we can write the equation for the particle executing simple harmonic motion

Comparing the equation with simple harmonic motion equation, we get

which means the angular frequency or natural frequency of the oscillator is

The frequency of the oscillation is

and the time period of the oscillation is
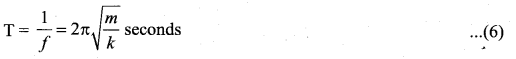
Question 11.
What is meant by free oscillation?
Answer:
When the oscillator is allowed to oscillate by displacing its position from equilibrium position, it oscillates with a frequency which is equal to the natural frequency of the oscillator. Such an oscillation or vibration is known as free oscillation or free vibration.
Question 12.
Explain damped oscillation. Give an example.
Answer:
The oscillations in which the amplitude decreases gradually with the passage of time are called damped Oscillations.
Example:
- The oscillations of a pendulum or pendulum oscillating inside an oil filled container.
- Electromagnetic oscillations in a tank circuit.
- Oscillations in a dead beat and ballistic galvanometers.
Question 13.
Define forced oscillation. Give an example.
Answer:
The body executing vibration initially vibrates with its natural frequency and due to the presence of external periodic force, the body later vibrates with the frequency of the applied periodic force. Such vibrations are known as forced vibrations.
Example: Sound boards of stringed instruments.
![]()
Question 14.
What is meant by maintained oscillation? Give an example.
Answer:
While playing in swing, the oscillations will stop after a few cycles, this is due to damping. To avoid damping we have to supply a push to sustain oscillations. By supplying energy from an external source, the amplitude of the oscillation can be made constant. Such vibrations, are known as maintained vibrations.
Example: The vibration of a tuning fork getting energy from a battery or from external power supply.
Question 15.
Explain resonance. Give an example.
Answer:
The frequency of external periodic force (or driving force) matches with the natural frequency of the vibrating body (driven). As a result the oscillating body begins to vibrate such that its amplitude increases at each step and ultimately it has a large amplitude. Such a phenomenon is known as resonance and the corresponding vibrations are known as resonance vibrations. Example: The breaking of glass due to sound
Samacheer Kalvi 11th Physics Oscillations Long Answer Questions
Question 1.
What is meant by simple harmonic oscillation? Give examples and explain why every simple harmonic motion is a periodic motion whereas the converse need not be true.
Answer:
Simple harmonic motion is a special type of oscillatory motion in which the acceleration or force on the particle is directly proportional to its displacement from a fixed point and is always directed towards that fixed point. In one dimensional case, let x be the .displacement of the particle and ax be the acceleration of the particle, then
![]()
where b is a constant which measures acceleration per unit displacement and dimensionally it is equal to T-2.
By multiplying by mass of the particle on both sides of equation (1) and from Newton’s second law, the force is
Fx = -kx …(3)
where k is a force constant which is defined as force per unit length. The negative sign indicates that displacement
and force (or acceleration) are in opposite directions. This means that when the displacement of the particle is taken towards right of equilibrium position (x takes positive value), the force (or acceleration) will point towards equilibrium (towards left) and similarly, when the displacement of the particle is taken towards left of equilibrium position (x takes negative value), the force (or acceleration) will point towards equilibrium (towards right). This type of force is known as restoring force because it always directs the particle executing simple harmonic motion to restore to its original (equilibrium or mean) position. This force (restoring force) is central and attractive whose center of attraction is the equilibrium position.
In order to represent in two or three dimensions, we can write using vector notation
![]()
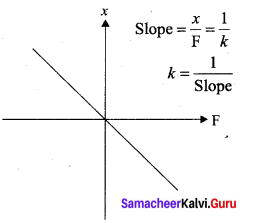
where \(\vec{r}\) is the displacement of the particle from the chosen origin. Note that the force and displacement have a linear relationship. This means that the exponent of force \(\overrightarrow{\mathrm{F}}\) and the exponent of displacement \(\vec{r}\) are unity. The sketch between cause (magnitude of force | \(\overrightarrow{\mathbf{F}}\) |) and effect (magnitude of displacement | \(\vec{r}\) |) is a straight line passing through second and fourth quadrant.
By measuring slope \(\frac{1}{k}\), one can find the numerical value of force constant k.
Question 2.
Describe Simple Harmonic Motion as a projection of uniform circular motion.
Answer:
The projection of uniform circular motion on a diameter of SHM
Consider a particle of mass m moving with uniform speed v along the circumference of a circle whose radius is r in anti-clockwise direction (as shown in figure). Let us assume that the origin of the coordinate system coincides with the center O of the circle. If ω is the angular velocity of the particle and θ the angular displacement of the particle at any instant of time t, then θ = ωt. By projecting the uniform circular motion on its diameter gives a simple harmonic motion. This means that we can associate a map (or a relationship) between uniform circular (or revolution) motion to vibratory motion. Conversely, any vibratory motion or revolution can be mapped to uniform circular motion. In other words, these two motions are similar in nature.
Let us first project the position of a particle moving on a circle, on to its vertical diameter or on to a line parallel to vertical diameter as shown in figure. Similarly, we can do it for horizontal axis or a line parallel to horizontal axis.
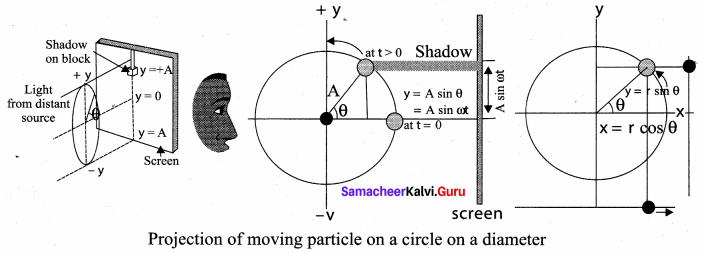
As a specific example, consider a spring mass system (or oscillation of pendulum). When the spring moves up and down (or pendulum moves to and fro), the motion of the mass or bob is mapped to points on the circular motion.
Thus, if a particle undergoes uniform circular motion then the projection of the particle on the diameter of the circle (or on a line parallel to the diameter) traces straight line motion which is simple harmonic in nature. The circle is known as reference circle of the simple harmonic motion. The simple harmonic motion can also be defined as the motion of the projection of a particle on any diameter of a circle of reference.
![]()
Question 3.
What is meant by angular harmonic oscillation? Compute the time period of angular harmonic oscillation.
Answer:
Time period and frequency of angular SHM:
When a body is allowed to rotate freely about a given axis then the oscillation is known as the angular oscillation. The point at which the resultant torque acting on the body is taken to be zero is called mean position. If the body is displaced from the mean position, then the resultant torque acts such that it is proportional to the angular displacement and this torque has a tendency to bring the body towards the mean position.
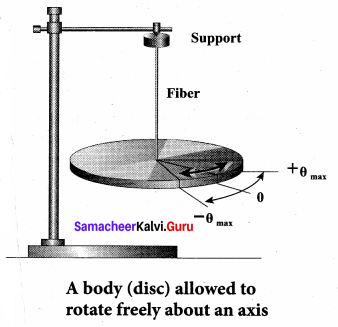
Let \(\vec{\theta}\) be the angular displacement of the body and the resultant torque \(\vec{\tau}\) acting on the body is

\(\kappa\) is the restoring torsion constant, which is torque per unit angular displacement. If I is the
moment of inertia of the body and a is the angular acceleration then

Question 4.
Write down the difference between simple harmonic motion and angular simple harmonic motion.
Answer:
Comparision of simple harmonic motion and angular harmonic motion

Question 5.
Discuss the simple pendulum in detail.
Answer:
Simple pendulum: A pendulum is a mechanical system which exhibits periodic motion. It has a bob with mass m suspended by a long string (assumed to be massless and inextensible string) and the other end is fixed on a stand. At equilibrium, the pendulum does not oscillate and hangs vertically downward. Such a position is known as mean position or equilibrium position. When a pendulum is displaced through a small displacement from its equilibrium position and released, the bob of the pendulum executes to and fro motion. Let l be the length of the pendulum which is taken as the distance between the point of suspension and the centre of gravity of the bob. Two forces act on the bob of the pendulum at any displaced position.
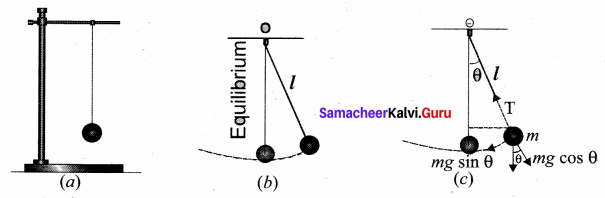
(i) The gravitational force acting on the body (\(\overrightarrow{\mathrm{F}}=m \vec{g}\)) which acts vertically downwards.
(ii) The tension in the string \(\overrightarrow{\mathrm{T}}\) which acts along the string to the point of suspension. Resolving the gravitational force into its components:
(a) Normal component: The component along the string but in opposition to the direction of tension, Fas = mg cos θ
(b) Tangential component: The component perpendicular to the string i.e., along tangential direction of arc of swing, Fps = mg sin θ
Therefore, The normal component of the force is, along the string,

From the figure, we can observe that the tangential component Wps of the gravitational force always points towards the equilibrium position i.e., the direction in which it always points opposite to the direction of displacement of the bob from the mean position. Hence, in this case, the tangential force is nothing but the restoring force. Applying Newton’s second law along tangential direction, we have

where, s is the position of bob which is measured along the arc. Expressing arc length in terms of angular displacement i.e.,

Because of the presence of sin 0 in the above differential equation, it is a non-linear differential equation (Here, homogeneous second order). Assume “the small oscillation approximation”, sin θ ≈ θ, the above differential equation becomes linear differential equation
![]()
This is the well known oscillatory differential equation. Therefore, the angular frequency of this oscillator (natural frequency of this system) is
Question 6.
Explain the horizontal oscillations of a spring.
Answer:
Horizontal oscillations of a spring-mass system: Consider a system containing a block of mass m attached to a massless spring with stiffness constant or force constant or spring constant k placed on a smooth horizontal surface (frictionless surface) as shown in figure. Let x0 be the equilibrium position or mean position of mass m when it is left undisturbed. Suppose the mass is displaced through a small displacement x towards right from its equilibrium position and then released, it will oscillate back and forth about its mean position Let F be the restoring force (due to stretching of the spring) which is proportional to the amount of displacement of block. For one dimensional motion, mathematically, we have
![]()
where negative sign implies that the restoring force will always act opposite to the direction of the displacement. This equation is called Hooke’s law. Notice that, the restoring force is linear with the displacement (i.e., the exponent of force and displacement are unity). This is not always true; in case if we apply a very large stretching force, then the amplitude
of oscillations becomes very large (which means, force is proportional to displacement containing higher powers of x) and
therefore, the oscillation of the system ìs not linear and hence, it is called non-linear oscillation. We restrict ourselves only to linear oscillations throughout our discussions, which means Hooke’s law is valid (force and displacement have a linear relationship).
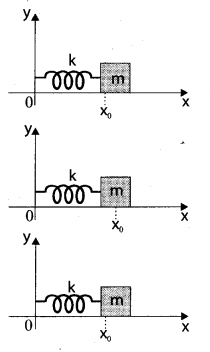
From Newton’s second law, we can write the equation for the particle executing simple harmonic motion
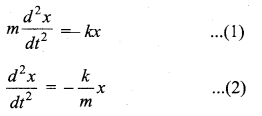
Comparing the equation with simple harmonic motion equation, we get
![]()
The frequency of the oscillation is
 >
>
and the time period of the oscillation is

Question 7.
Describe the vertical oscillations of a spring.
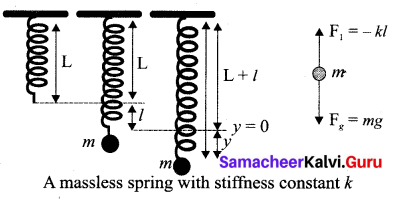
Answer:
Vertical oscillations of a spring: Let us consider a massless spring with stiff ness constant or force constant k attached to a ceiling as shown in figure. Let the length of the spring before loading mass m be L. If the block of mass m is attached to the other end of spring, then the spring elongates by a length l. Let F1 be the restoring force due to stretching of spring. Due to mass m, the gravitational force acts vertically downward. We can draw free-body diagram for this system as shown in figure. When the system is under equilibrium,
F1 + mg = 0 …(1)
But the spring elongates by small displacement /, therefore,
![]()
Substituting equation (2) in equation (1), we get
-kl + mg = 0

Suppose we apply a very small external force on the mass such that the mass further displaces downward by a displacement y, then it will oscillate up and down. Now, the restoring force due to this stretching of spring (total extension of spring is y +1) is
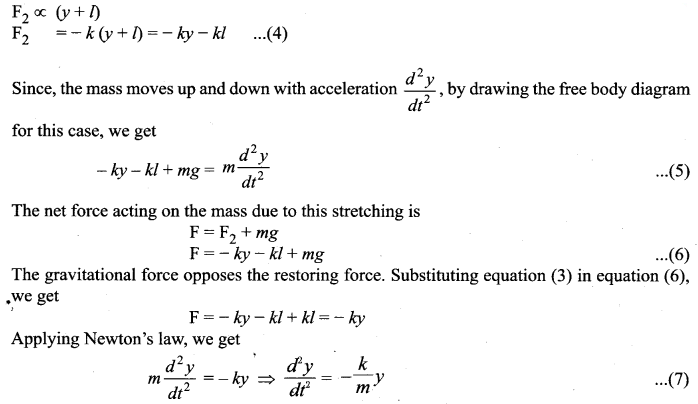
The above equation is in the form of simple harmonic differential equation. Therefore, we get the time period as

Question 8.
Write short notes on the oscillations of liquid column in U-tube.
Answer:
Oscillation of liquid in a U-tube:
Consider a U-shaped glass tube which consists of two open arms with uniform cross sectional area A. Let us pour a non- viscous uniform incompressible liquid of density ρ in the U-shaped tube to a height h as shown in the figure. If the liquid and tube are not disturbed then the liquid surface will be in equilibrium position O.
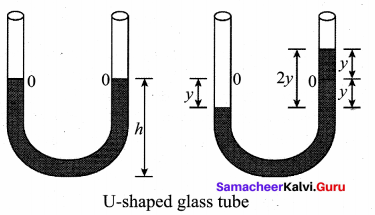
It means the pressure as measured at any point on the liquid is the same and also at the surface on the arm (edge of the tube on either side), which balances with the atmospheric pressure. Due to this the level of liquid in each arm will be the same. By blowing air one can provide sufficient force in one arm, and the liquid gets disturbed from equilibrium position O, which means, the pressure at blown arm is higher than the other arm. This creates difference in pressure which will cause the liquid to oscillate for a very short duration of time about the mean or equilibrium position and finally comes to rest. Time period of the oscillation is
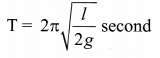
![]()
Question 9.
Discuss in detail the energy in simple harmonic motion.
Answer:
Energy in simple harmonic motion:
(a) Expression for Potential Energy
For the simple harmonic motion, the force and the displacement are related by Hooke’s law
\(\overrightarrow{\mathrm{F}}=-k \vec{r}\)
Since force is a vector quantity, in three dimensions it has three components.
Further, the force in the above equation is a conservative force field; such a force can be derived from a scalar function which has only one component. In one dimensional case
F = — kx …… (1)
The work done by the conservative force field is independent of path. The potential energy U can be calculated from the following expression.
![]()
Comparing (1) and (2), we get
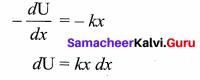
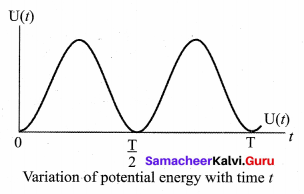
This work done by the force F during a small displacement dx stores as potential energy

where ω is the natural frequency of the oscillating system. For the particle executing simple harmonic motion from equation y = A sift ωt, we get
x = A sin ωt
![]()
This variation of U is shown in figure.
(b) Expression for Kinetic Energy
Kinetic energy
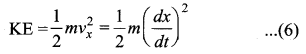
Since the particle is executing simple harmonic motion, from equation
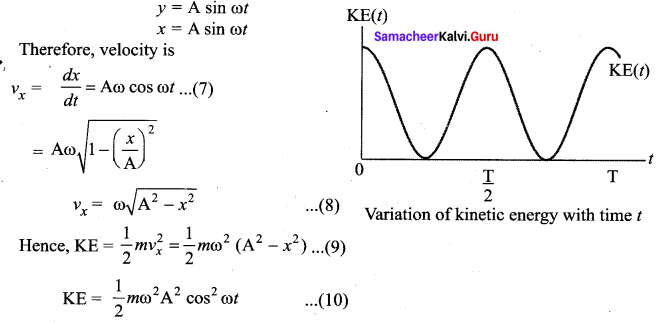
This variation with time is shown in figure.
(c) Expression for Total Energy
Total energy is the sum of kinetic energy and potential energy
E = KE + U …(11)
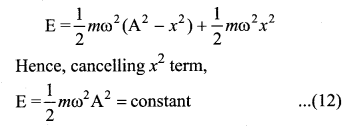
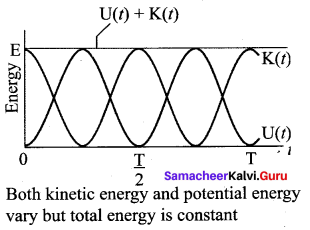
Alternatively, from equation (5) and equation (10), we get the total energy as
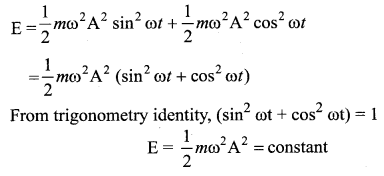
which gives the law of conservation of total energy.
Thus the amplitude of simple harmonic oscillator, can be expressed in terms of total energy.

Question 10.
Explain in detail the four different types of oscillations.
Answer:
Free oscillations: When the oscillator is* allowed to oscillate by displacing its position from equilibrium position, it oscillates with a frequency which is equal to the natural frequency of the oscillator. Such an oscillation or vibration is known as free oscillation or free vibration. In this case, the amplitude, frequency and the energy of the vibrating object remains constant.
Examples:
- Vibration of a tuning fork.
- Vibration in a stretched string.
- Oscillation of a simple pendulum.
- Oscillations of a spring-mass system.
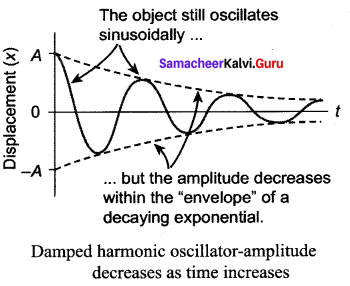
Damped oscillations: During the oscillation of a simple pendulum (in previous case), we have assumed that the amplitude of the oscillation is constant and also the total energy of the oscillator is constant. But in reality, in a medium, due to the presence of friction and air drag, the amplitude of oscillation decreases as time progresses. It implies that the oscillation is not sustained and the energy of the SHM decreases gradually indicating the loss of energy.
The energy lost is absorbed by the surrounding medium. This type of oscillatory motion is known as damped oscillation. In other words, if an oscillator moves in a resistive medium, its amplitude goes on decreasing and the energy of the oscillator is used to do work against the resistive medium. The motion of the oscillator is said to be damped and in this case, the resistive force (or damping force) is proportional to the velocity of the oscillator.
Examples:
- The oscillations of a pendulum (including air friction) or pendulum oscillating inside an oil filled container.
- Electromagnetic oscillations in a tank circuit.
- Oscillations in a dead beat and ballistic galvanometers.
Maintained oscillations: While playing in swing, the oscillations will stop aft er a few cycles, this is due to damping. To avoid damping we have to supply a push to sustain oscillations. By supplying energy from an external source, the amplitude of the oscillation can be made constant. Such vibrations are known as maintained vibrations.
Example: The vibration of a tuning fork getting energy from a battery or from external power supply.
Forced oscillations: Any oscillator driven by an external periodic agency to overcome the damping is known as forced oscillator or driven oscillator. In this type of vibration, the body executing vibration initially vibrates with its natural frequency and due to the presence of external periodic force, the body later vibrates with the frequency of the applied periodic force. Such vibrations are known as forced vibrations.
Example: Sound boards of stringed instruments.
Samacheer Kalvi 11th Physics Oscillations Numerical Problems
Question 1.
Consider the Earth as a homogeneous sphere of radius R and a straight hole is bored in it through its centre. Show that a particle dropped into the hole will execute a simple harmonic motion such that its time period is
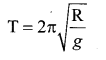
Answer:
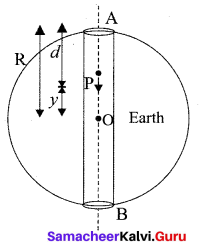
Oscillations of a particle dropped in a tunnel along the diameter of the earth.
Consider earth to be a sphere of radius R and centre O. A straight tunnel is dug along the diameter of the earth. Let ‘g’ be the value of acceleration due to gravity at the surface of the earth.
Suppose a body of mass ‘m’ is dropped into the tunnel and it is at point R i.e., at a depth d below the surface of the earth at any instant.
If g’ is acceleration due to gravity at P.
![]()
If y is distance of the body from the centre of the earth, then
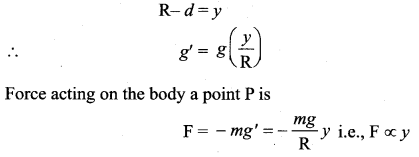
Negative sign indicates that the force acts in the opposite direction of displacement.
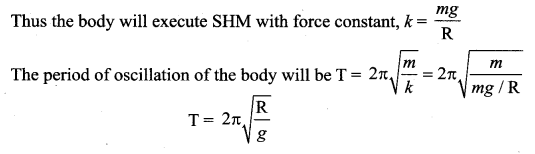
![]()
Question 2.
Calculate the time period of the oscillation of a particle of mass m moving in the potential defined as 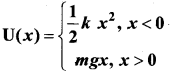
Answer:

Question 3.
Consider a simple pendulum of length l = 0.9 m which is properly placed on a trolley rolling down on a inclined plane which is at θ = 45° with the horizontal. Assuming that the inclined plane is frictionless, calculate the time period of oscillation of the simple pendulum.
Answer:
Length of the pendulum l = 0.9 m
Inclined angle θ = 45°

Question 4.
A piece of wood of mass m is floating erect in a liquid whose density is p. If it is slightly pressed down and released, then executes simple harmonic motion. Show that its time period of oscillation is 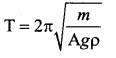
Answer:
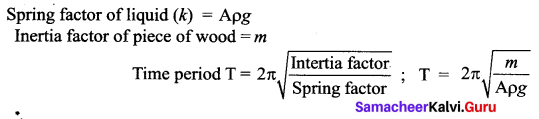
Question 5.
Consider two simple harmonic motion along x and y-axis having same frequencies but different amplitudes as x = A sin (ωt + φ) (along x axis) and y = B sin ωt (along y axis).
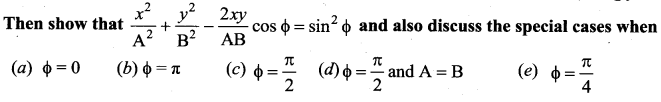
Note: when a particle is subjected to two simple harmonic motion at right angle to each other the particle may move along different paths. Such paths are called Lissajous figures.
Answer:
(a) \(y=\frac{\mathrm{B}}{\mathrm{A}} x\), equation is a straight line passing through origin with positive slope.
(b) \(y=-\frac{B}{A} x\), equation is a straight line passing through origin with negative slope.
(c) \(\frac{x^{2}}{\mathrm{A}^{2}}+\frac{y^{2}}{\mathrm{B}^{2}}=1\), equation is an ellipse whose center is origin. A2 B2
(d) \(x^{2}+y^{2}=\mathrm{A}^{2}\), equation is a circle whose center is origin.
(e) \(\frac{x^{2}}{\mathrm{A}^{2}}+\frac{y^{2}}{\mathrm{B}^{2}}-\frac{2 x y}{\mathrm{AB}} \frac{1}{\sqrt{2}}=\frac{1}{2}\), equation is an ellipse which (oblique ellipse which means tilted ellipse)
![]()
Question 6.
Show that for a particle executing simple harmonic motion
(a) the average value of kinetic energy is equal to the average value of potential energy.
(b) average potential energy = average kinetic energy = \(\frac{1}{2}\) (total energy)
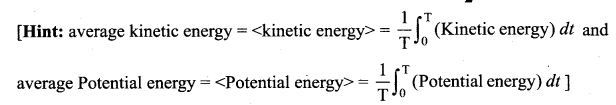
Suppose a particle of mass m executes SHM of period T. The displacement of the particles at any instant t is given by y = A sin ωt

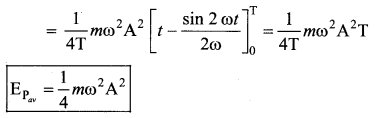
Question 7.
Compute the time period for the following system if the block of mass m is slightly displaced vertically down from Its equilibrium position and then released. Assume that the pulley is light and smooth, strings and springs are light.
Answer:
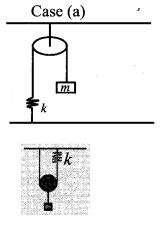
Case (a): Pulley is fixed rigidly here. When the mass displace by y and the spring will also stretch by y. Therefore, F = T = ky
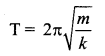
Case (b): Mass displace by y, pulley also displaces by y. T = 4ky

Samacheer Kalvi 11th Physics Oscillations Additional Questions
Question 1.
The total energy of a particle vibrating in SHM is proportional to the square of its ……..
(a) velocity
(b) acceleration
(c) amplitude
(d) none of these
Answer:
(a) veloctiy
Question 2.
In order to double the period of a simple pendulum ……….
(a) its length should doubled
(b) its length should be quadrupled.
(c) the mass of its bob should be doubled.
(d) the mass of its bob should be quadrupled.
Answer:
(b) its length should be quadrupled.
Question 3.
A simple harmonic oscillator has amplitude A and time period T. Its maximum speed is …….

Answer:
(d) \(\frac{2 \pi \mathrm{A}}{\mathrm{T}}\)
Solution:
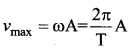
Question 4.
A simple harmonic oscillator has a period of 0.01 s and an amplitude of 0.2 m. The magnitude of the velocity in m/s at the centre of oscillation is ……..
(a) 20π
(b) 40π
(c) 60π
(d) 80π
Answer:
(b) 40π
Solution:
Velocity is maximum at the centre of oscillation and is given by
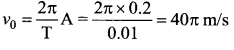
Question 5.
A particle is executing SHM. Then the graph of acceleration as a function of displacement is ……..
(a) straight line
(b) circle
(c) ellipse
(d) hyperbola
Answer:
(a) straight line
Solution:
In SHM, F ∝ y ⇒ a ∝ y; Thus the graph is a straight line.
Question 6.
A particle is executing SHM. Then the graph of velocity as a function of displacement is …….
(a) straight line
(b) circle
(c) ellipse
(d) hyperbola
Answer:
(c) ellipse
Solution:
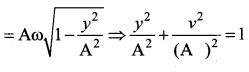
![]()
Question 7.
The amplitude of a vibrating body situated in a resisting medium ………
(a) decreases linearly with time
(b) decrease exponentially with time
(c) decreases with time in some other manner
(d) remains constant with time
Answer:
(b) decreases exponentially with time
Question 8.
The frequency of a vibrating body situated in air …….
(a) is the same as its natural frequency
(b) is higher than its natural frequency
(c) is lower than its natural frequency
(d) can have any value
Answer:
(c) is lower than its natural frequency
Question 9.
The equation 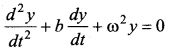 represents the equation of motion for a ……. vibration
represents the equation of motion for a ……. vibration
(a) free
(b) damped
(c) forced
(d) resonant
Answer:
(b) damped
Question 10.
The displacement equation of an oscillator is y = 5 sin (0.2 7 πt + 0.5 π) in SI units. The time period of oscillation is
(a) 10 s
(b) 1 s
(c) 0.2 s
(d) 0.5 s
Answer:
(a) 10 s
Solution:
Comparing with the standard equation y = A sin (ωt + φ)
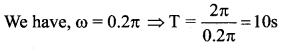
![]()
Question 11.
A loaded spring vibrates with a period T. The spring is divided into four equal parts and the same load is suspended from one as these parts. The new time period is ………

Answer:
(b) \(\frac{\mathrm{T}}{2}\)
Solution:
Let the force constant of the spring be k. Then T = \(2 \pi \sqrt{\frac{m}{k}}\)
If the spring is divided into four equal parts, then the force constant of each part will be 4k.
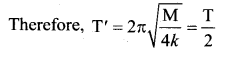
Question 12.
The vertical extension in a light spring by a weight of 1 kg, in equilibrium is 9.8 cm. The period of oscillation of the spring, in seconds, will be ……

Answer:
(a) \(\frac{2 \pi}{10}\)
Solution:
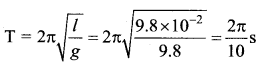
Question 13.
A particle executing SHM has an acceleration of 64 cm/s2 with its displacement is 4 cm. Its time period, in seconds is ……
![]()
Answer:
(a) \(\frac{\pi}{2}\)
Solution:
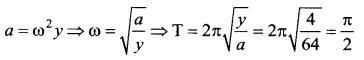
Question 14.
A body executes SHM with an amplitude A. Its energy is half kinetic and half potential when the displacement is ……..

Answer:
\(\frac{\mathrm{A}}{\sqrt{2}}\)
Solution:
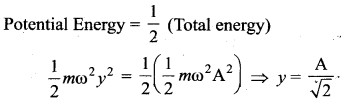
Question 15.
The maximum displacement of a particle executing SHM is 1 cm and the maximum acceleration is (1.57)2 cm/s2. Its time period is …..
(a) 0.25s
(b) 4.0s
(c) 1.57s
(d) 3.14s
Answer:
(b) 4.0s
Solution:

![]()
Question 16.
The velocity of a particle, undergoing SHM is v at the mean position. If its amplitude is doubled, the velocity at the mean position will be …….
(a) 2 v
(b) 3 v
(c) \(2 \sqrt{2} v\)
(d) 4v
Answer:
(a) 2 v
Solution:
![]()
Question 17.
A girl is swinging on a swing in the sitting position. How will the period of swing be affected if she stands up?
(a) The period will now be shorter
(b) The period will now be longer
(c) The period will remain unchanged
(d) The period may become longer or shorter depending upon the height of the girl
Answer:
(a) The period will now be shorter
Solution:
The effective value of I will decrease. Therefore, the time period will be shorter.
Question 18.
The equation of SHM of a particle is 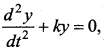 > where k is a positive constant. The time period of motion is given by …….
> where k is a positive constant. The time period of motion is given by …….

Answer:
(a) \(\frac{2 \pi}{\sqrt{k}}\)
Solution:
Here k is same as ω2
Question 19.
The amplitude of a damped oscillator becomes half in one minute. The amplitude after 3 minutes will be \(\frac{1}{x}\) time the original, where x is ………
(a) 2 × 3
(b) 23
(c) 32
(d) 3 × 22
Answer:
(b) 23
Solution:
The amplitude decreases exponentially with time and becomes half in 1 minute.
Amplitude after 3 minutes = \(\left(\frac{1}{2}\right)^{3}\) of the original value. Thus, x = 23
![]()
Question 20.
When the potential energy of a particle executing simple harmonic motion is one-fourth of its maximum value during the oscillation, the displacement of the particle from the equilibrium position in terms of its amplitude a is ……..
![]()
Answer:
(c) \(\frac{a}{2}\)
Solution:
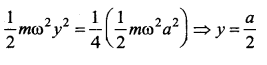
Question 21.
A massless spring, having force constant k, oscillates with a frequency n when a mass m is suspended from it. The spring is cut into two equal halves and a mass 2m is suspended from one of the parts. The frequency of oscillation will now be
For a simple pendulum the graph between length and time period will be …….
(a) n
(b) \(n \sqrt{2}\)
(c) \(\frac{n}{\sqrt{2}}\)
(d) 2n
Answer:
(a) n
Solution:
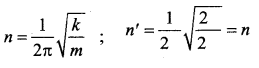
Question 22.
For a simple pendulum the graph between the length and time period will be a ……….
(a) hyperbola
(b) Parabola
(c) Straight line
(d) none of these
Answer:
(b) Parabola
Question 23.
A particle is executing simple harmonic motion given by 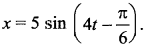 The velocity of the particle when its displacement is 3 units is …….
The velocity of the particle when its displacement is 3 units is …….
![]()
Answer:
(a) 16 units
Solution:
![]()
Question 24.
When a particle oscillates simple harmonically, its potential energy varies periodically. If the frequency of oscillation of the particle is n, the frequency of potential energy variation is ……
(a) \(\frac{n}{2}\)
(b) n
(c) 2n
(d) 4n
Answer:
(c) 2n
![]()
Question 25.
A particle, moving along the x-axis, executes simple harmonic motion when the force acting on it is given by (A and k are positive constants.) …….
(a) – Akx
(b) A cos (kx)
(c) A exp (- kx)
(d) Akx
Answer:
(a) – Akx
Question 26.
The motion of a particle is expressed by the equation a = -bx, where x is the displacement from the mean position, a is the acceleration and b is a constant. The periodic time is ………

Answer:
(b) \(\frac{2 \pi}{\sqrt{b}}\)
Solution:
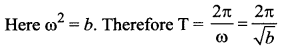
Question 27.
The angular velocity and the amplitude of a simple pendulum are ω and a, respectively. The ratio of its kinetic and potential energies at a displacement x from the mean position is ……….

Solution:
(d) \(\frac{a^{2}-x^{2}}{x^{2}}\)
Solution:
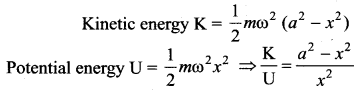
Question 28.
A particle is oscillating according to the equation x = 5 cos (0.5 π t) where t is in seconds. The particle moves from the position of equilibrium to the position of maximum displacement in time ………
(a) 1 s
(b) 2 s
(c) 0.5 s
(d) 4 s
Answer:
(a) 1 s
Solution:
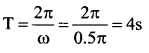
Time taken to move from the position of equilibrium to the position of maximum displacement is t = \(\frac{T}{4}\) = 1s
Question 29.
A seconds pendulum is placed in a space laboratory orbiting around the Earth at a height 3R from the Earth’s surface where R is the radius of the Earth. The time period of the pendulum will be ……..
(a) zero
(b) 2/3s
(c) 4 s
(d) infinite
Answer:
(d) infinite
Solution:
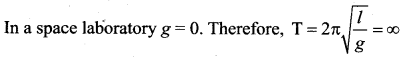
Question 30.
A mass m is vertically suspended from a spring of negligible mass; the system oscillates with a frequency n. What will be the frequency of the system, if a mass 4m is suspended from the same spring?

Answer:
(a) \(\frac{n}{2}\)
Solution:
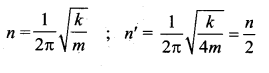
Question 31.
Two simple pendulums of lengths 0.5m and 2.0m respectively are given small linear displacement in one direction at the same time. They will again be in phase when the pendulum of shorter length has completed …….. oscillations.
(a) 5
(b) 3
(c) 1
(d) 2
Answer:
(d) 2
Solution:
The time period of the shorter pendulum is half that of the longer pendulum. Therefore, the pendulums will again be in phase ( at the mean position). When the shorter pendulum has completed 2 oscillations.
![]()
Question 32.
A body is executing simple harmonic motion with an angular frequency 2 rod/sec. The velocity of the body at 20mm displacement, when the amplitude of motion is 60mm, is
(a) 90mm/s
(b) 113mm/s
(c) 118 mm/s
(d) 131 mm/s
Answer:
(b) 113 mm/s
Solution:
![]()
Question 33.
If the displacement of a particle executing SHM, is given by y = 0.30 sin (220t + 0.64) in metre, then the frequency and the maximum velocity of the particle are (t is in seconds)
(a) 35 Hz, 66m/s
(b) 45 Hz, 66 m/s
(c) 58 Hz, 113 m/s
(d) 35 Hz, 132 m/s
Answer:
(a) 35 Hz, 66 m/s
Solution:
![]()
Question 34.
The kinetic energy of a particle, executing SHM, is 16 J when it is at its mean position. If the amplitude of oscillations is 25 cm, and the mass of the particle is 5.12 kg, the time period of its oscillation is …….
(a) π/5 s
(b) 2π s
(c) 20π s
(d) 5π s
Answer:
(a) π/5 s
Solution:

Question 35.
A particle of mass m is executing oscillations about the origin on the x-axis. Its potential energy is V(x) = kx2 .Where k is a positive constant. If the amplitude of oscillation is a, then its time period T is

Answer:
(b) independent of a
Solution:
Since V(x) = Kx2, the motion is simple harmonic. In SHM, the time period is independent of the amplitude of oscillation.
Question 36.
The amplitude of a damped oscillation reduces to one third of its original value a0 in 20s. The amplitude of such oscillation after a period of 40s will be ……..
(a) a0/9
(b) a0/6
(c) a0/2
(d) a0/27
Answer:
(a) a0/9
Solution:
In the first 20s, the amplitude reduces to one-third of the original value, i.e., to a0/3, In the next 20s, it will reduce to one-third of the reduced value, i.e., to a0/9.
Question 37.
Masses mA and mB hanging from the ends of strings of lengths lA and lB are executing. Simple harmonic motions. If their frequencies are related as fA= 2fB, then ……

Answer:
(c) lA = lB/4 regardless of masses.
Solution:
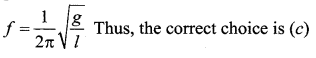
Question 38.
Two simple harmonic motions act on a particle. These harmonic motions are x = A cos (ωt + δ); y = A cos (ωt + α) When ![]() the resulting motion is …….
the resulting motion is …….
(a) A circle and the actual motion is clockwise
(b) an ellipse and the actual motion is counter clockwise
(c) a ellipse and the actual motion is clockwise
(d) a circle and the actual motion is counter clockwise
Answer:
(d) a circle and the actual motion is counter clockwise
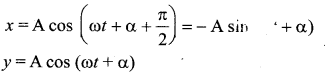
Solution:
Squaring and adding the two equations, We get x2 + y2 = A2. This is an equation of a circle. Hence the resultant motion is circular. The motion is counter clockwise.
Question 39.
A metal bob is suspended from a coiled spring. When set into vertical vibrations on the earth. It oscillates up and down with frequency f If the same experiment is carried out in a satellite circling the Earth the frequency of vibration will be …….
(a) f
(b) zero
(c) infinite
(d) depend on the distance of the satellite from the earth.
Answer:
(a) f
Solution:
The frequency of oscillation of a mass spring system depends only on the mass and the spring constant.
![]()
Question 40.
In forced oscillations of a particle, the amplitude is maximum for a frequency ω1 of the force, while the energy is maximum for a frequency ω2 of the force. Then ……
(a) ω1 < ω2
(b) ω1 > ω2 when damping is small and ω1 > ω2 when damping is large.
(c) ω1 > ω2
(d) ω1 = ω2
Answer:
(d) ω1 = ω2
Question 41.
Which one of the following statements is true for the speed v and the acceleration a of a particle executing simple harmonic motion?
(a) When v is maximum, a is maximum
(b) Value of a is zero, whatever may be the value of v
(c) When v is zero, a is zero
(d) When v is maximum, a is zero
Answer:
(d) When v is maximum, a is zero
Solution:
![]()
Question 42.
The function sin2 (ωt) represents
(a) a simple harmonic motion with a period π/ω
(b) a simple harmonic motion with a period 2π/ω
(c) a periodic, but not simple harmonic motion with a period π/ω
(d) a periodic, but not simple harmonic motion with a period 2π/ω
Answer:
(a) a simple harmonic motion with a period π/ω
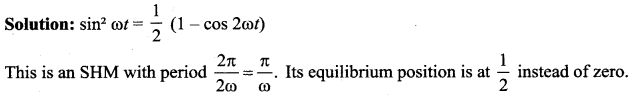
Question 43.
A particle executing simple harmonic motion has a kinetic energy K0 cos2 ωt. The maximum
values of the potential energy and the total energy are, respectively ….
(a) k0/2 and k0
(b) k0 and 2k0
(c) k0 and k0
(d) 0 and 2k0
Answer:
(c) k0 and k0
Question 44.
A particle executing simple harmonic motion of amplitude 31.4 cm/s. The frequency of its oscillation is ………
(a) 3 Hz
(b) 4 Hz
(c) 2 Hz
(d) 1 Hz
Answer:
(d) 1 Hz
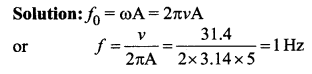
Question 45.
The phase difference between the instantaneous velocity and acceleration of a particle executing simple harmonic motion is ……..
(a) 0.5π
(b) π
(c) 0.707π
(d) zero
Answer:
(a) 0.5π
Question 46.
Which one of the following equations of motion represents simple harmonic motion?
(a) Acceleration = – k0x + k1x2
(b) Acceleration = – k(x + a)
(c) Acceleration = k(x + a)
(d) Acceleration = kx
Answer:
(b) Acceleration = k(x + a)
Question 47.
Which of the following functions represent SHM?

(a) I and III
(b) I and II
(c) only I
(d) I, II and III
Answer:
(a) I and III
Question 48.
Two simple harmonic motions of angular frequencies 100 and 1000 rad/s have the same displacement amplitude. The ratio of their maximum accelerations is ……….
(a) 1 : 10
(b) 1 : 102
(c) 1 : 103
(d) 1 : 104
Answer:
(b) 1 : 10
Solution:
The magnitude of the maximum acceleration is given by
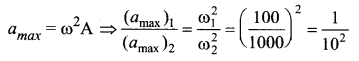
Question 49.
The period of oscillation of a simple pendulum is T in a stationary lift. If the lift moves upwards with an acceleration of 8g, the period will ……..
(a) remain the same
(b) decrease by T/2
(c) increase by T/3
(d) none of these
Answer:
(c) increase by T/3
Solution:
Thus, the new time period is T/3. Hence the correct option is (d).
![]()
Question 50.
A simple harmonic oscillator consist of a particle of mass m and an ideal spring with spring constant k The particle oscillates with a time period T. The spring is cut into two equal parts. If one part oscillates with the same particle, the time period will be …….
![]()
Answer:
(b) \(\frac{\mathrm{T}}{\sqrt{2}}\)
Solution:
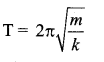
If the spring is cut into two equal parts, the force constant of each part becomes 2k. Therefore,
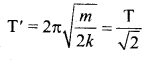
Question 51.
A particle executing simple harmonic motion of amplitude 5 cm has maximum speed of 31.4 cm/s. The frequency of its oscillation is …….
(a) 3 Hz
(b) 4 Hz
(c) 2 Hz
(d) 1 Hz
Answer:
(d) 1 Hz
Solution:
![]()
Samacheer Kalvi 11th Physics Oscillations 2 Marks Questions
Question 1.
What is meant by Oscillatory motion?
Answer:
When an object or a particle moves back and forth repeatedly for some duration of time, its – motion is said to be oscillatory (or vibratory).
Question 2.
What is meant by simple harmonic motion (SHM)?
Answer:
A particle is said to execute simple harmonic motion if it moves to and fro about a mean position under the action of a restoring force which is directly proportional to its displacement from the mean position and is always directed towards the mean position.
Question 3.
What is meant by displacement in SHM?
Answer:
The distance travelled by the vibrating particle at any instant of time t from its mean position is known as displacement.
y = A sin ωt
The maximum displacement from the mean position is known as amplitude (A) of the vibrating particle.
Question 4.
Define velocity in SHM.
Answer:
Velocity: The rate of change of displacement is velocity.
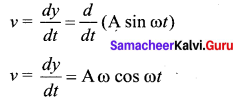
Question 5.
Define acceleration in SHM.
Answer:
Acceleration: The rate of change of velocity is acceleration.
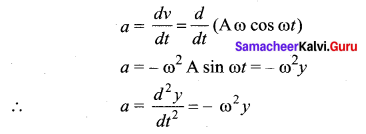
![]()
Question 6.
What is meant by phase in SHM?
Answer:
Phase: The phase of a vibrating particle at any instant completely specifies the state of the particle. It expresses the position and direction of motion of the particle at that instant with respect to its mean position.
Question 7.
What is meant by angular oscillation?
Answer:
When a body is allowed to rotate freely about a given axis then the oscillation is known as the angular oscillation.
Question 8.
Define Amplitude.
Answer:
The maximum displacement of the oscillating particle on either side of its mean position is called its amplitude.
Samacheer Kalvi 11th Physics Oscillations 3 Marks Questions
Question 1.
Derive the expression for resultant spring constant when two springs having constant k1 and k2 are connected in series.
Answer:
Let x1 and x2 be the elongation of springs from their equilibrium position (un-stretched position) due to applied force F. Then, the net displacement of the mass point is
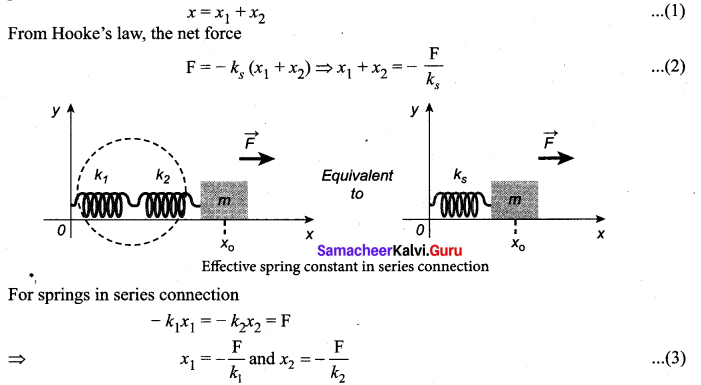
Therefore, substituting equation (3) in equation (2), the effective spring constant can be calculated as

Suppose we have n springs connected in series, the effective spring constant in series is
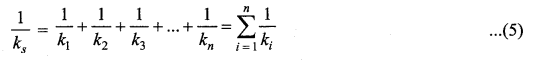
If all spring constants are identical i.e., k1 = k2 = … = kn = k then

This means that the effective spring constant reduces by the factor n. Hence, for springs in series connection, the effective spring constant is lesser than the individual spring constants. From equation (3), we have,
![]() >
>
Then the ratio of compressed distance or elongated distance x1 and x2 is
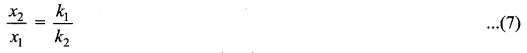
The elasticity potential energy stored in first and second springs are ![]() respectively. Then their ratio is
respectively. Then their ratio is

![]()
Question 2.
Derive the expression for resultant spring constant when two springs having constant k1 and k2 are connected in parallel.
Answer:
k1 and k2 attached to a mass m as shown in figure. The results can be generalized to any number of springs in parallel.
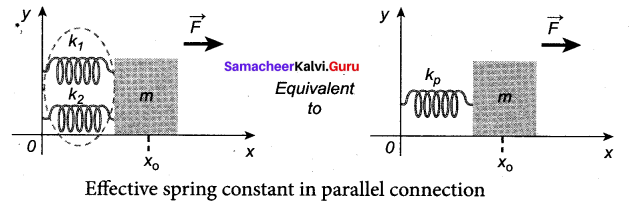
Let the force F be applied towards right as shown in figure. In this case, both the springs elongate or compress by the same amount of displacement. Therefore, net force for the displacement of mass m is
F = – kpX …(1)
where kp is called effective spring constant.
Let the first spring be elongated by a displacement x due to force F1 and second spring be elongated by the same displacement x due to force F2, then the net force
F = – k1x – k2x …..(2)
Equating equations (2) and (1), we get
kp = k1 + k2…..(2)
Generalizing, for n springs connected in parallel,

If all spring constants are identical i.e., k1 = kk2 = … = kn = k then
![]()
This implies that the effective spring constant increases by a factor n. Hence, for the springs in parallel connection, the effective spring constant is greater than individual spring constant.
Samacheer Kalvi 11th Physics Oscillations Numerical Problems
Question 1.
A pendulum is hung from the roof of a sufficiently high building and is moving freely to and fro like a simple harmonic oscillator. The acceleration of the bob of the pendulum oscillator. The acceleration of the bob of the pendulum is 20 ms-2 at a distance of 5 m from the mean position. To find the time period of oscillation.
Answer:
Given; a = 20ms-2 ; y = 5 m a = ω2y
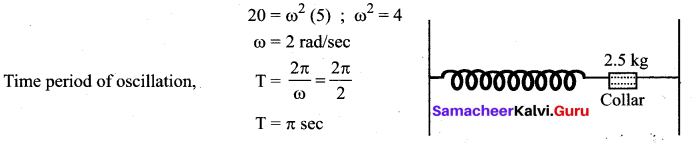
Question 2.
The acceleration due to gravity on the surface of the moon is 1.7 ms-2. What is the time period of simple pendulum on the moon if its time period on the earth is 3.5 s? Give g on Earth = 9.8 ms-2
Answer:

![]()
Question 3.
A particle executes linear simple harmonic motion with an amplitude of 3 cm. When the particle is at 2 cm from the mean position, the magnitude of its velocity is equal to that of its acceleration. Then find its time period in seconds.
Answer:

Question 4.
A body of mass m is attached to lower end of a spring whose upper end is fixed. The spring has negligible mass. When the mass m is slightly pulled down and released, it oscillates with a time period of 3s. When the mass m is increased by 1 kg, the time period of oscillations becomes 5s. Find the value of m is kg.
Answer:
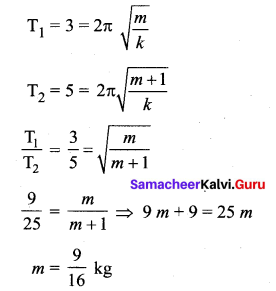
Question 5.
Two simple harmonic motions are represented by the equations:
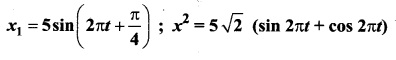
What is the ratio of their amplitudes ?
Answer:

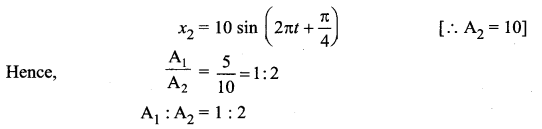
![]()
Question 6.
A block whose mass is 1 kg is fastened to a spring. The spring has a spring constant of 50 Nm-1. The block is pulled to a distance x = 10 cm from its equilibrium position at t = 0 on a frictionless surface from rest at t = 0. Calculate the kinetic, potential and total energies of the block when it is 5 cm away from the mean position.
Answer:
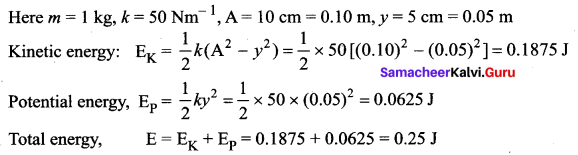
Question 7.
A 5 kg collar is attached to a spring of force constant 500 Nm-1. It slides without friction on a horizontal rod as shown in figure. The collar is displaced from its equilibrium position by 10.0 cm and released.
Calculate:
(i) the period of oscillation
(ii) the maximum speed, and
(iii) the maximum acceleration of the collar.
Answer:

Question 8.
A 0.2 kg of mass hangs at the end of a spring. When 0.02 kg more mass is added to the end of the spring, it stretches 7 cm more. If the 0.02 kg mass is removed, what will be the period of vibration of the system?
Answer:
When 0.02 kg mass is added, the spring streches by 7 cm
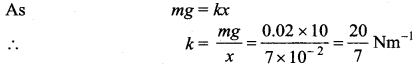
When 0.02 kg mass ia removed, the period of vibration will be
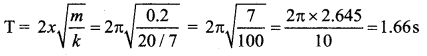
![]()
Question 9.
A mass M is suspended from a spring of negligible mass. The spring is pulled a little and then released so that the mass executes SHM of time period T. If the mass is increased by m, the time period becomes 5T/3. What is the ratio m/M?
Answer:
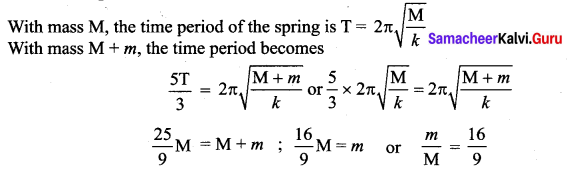
Question 10.
A body describes simple harmonic motion with an amplitude of 5 cm and a period of 0.2s. Find the acceleration and velocity of the body when the displacement is 5 cm.
Answer:
Here A = 5 cm, T = 0.2s
Velocity and acceleration at any displacement x are given by
