Students can Download Physics Chapter 1 Nature of Physical World and Measurement Questions and Answers, Notes Pdf, Samacheer Kalvi 11th Physics Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Physics Solutions Chapter 1 Nature of Physical World and Measurement
Samacheer Kalvi 11th Physics Nature of Physical World and Measurement TextBook Questions Solved
Samacheer Kalvi 11th Physics Nature of Physical World and Measurement Multiple Choice Questions
Question 1.
One of the combinations from the fundamental physical constants is \(\frac{h c}{\mathrm{G}}\). The unit of this expression is
(a) Kg2
(b) m3
(c) S-1
(d) m
Answer:
(a) Kg2
![]()
Question 2.
If the error in the measurement of radius is 2%, then the error in the determination of volume of the sphere will be …….
(a) 8%
(b) 2%
(c) 4%
(d) 6%
Answer:
(d) 6%
![]()
Question 3.
If the length and time period of an oscillating pendulum have errors of 1 % and 3% respectively
then the error in measurement of acceleration due to gravity is …… [Related to AMPMT 2008]
(a) 4%
(b) 5%
(c) 6%
(d) 7%
Answer:
(d) 7%
Question 4.
The length of a body is measured as 3.51 m, if the accuracy is 0.01mm, then the percentage error in the measurement is ……
(a) 351%
(b) 1%
(c) 0.28%
(d) 0.035%
Answer:
(c) 0.28%
Question 5.
Which of the following has the highest number of significant figures?
(a) 0.007 m2
(b) 2.64 × 1024 kg
(c) 0.0006032 m2
(d) 6.3200 J
Answer:
(d) 6.3200 J
Question 6.
If π = 3.14, then the value of π2 is …..
(a) 9.8596
(b) 9.860
(c) 9.86
(d) 9.9
Answer:
(c) 9.86
Question 7.
Which of the following pairs of physical quantities have same dimension?
(a) force and power
(b) torque and energy
(c) torque and power
(d) force and torque
Answer:
(b) torque and energy
![]()
Question 8.
The dimensional formula of Planck’s constant h is [AMU, Main, JEE, NEET]
(a) [ML2T-1]
(b) [ML2T-3]
(c) [MLTT-1]
(d) [MLTT3-3]
Answer:
(a) [ML2T-1]
Question 9.
The velocity of a particle v at an instant t is given by v = at + bt2. The dimensions of b is ……
(a) [L]
(b) [LT-1]
(c) [LT-2]
(d) [LT-3]
Answer:
(d) [LT-3]
Question 10.
The dimensional formula for gravitational constant G is [Related to AIPMT 2004]
(a) [ML-3T-2]
(b) [M-1L3T-2]
(c) [M-1L-3T-2]
(d) [ML-3T2]
Answer:
(b) [M-1L3T-2]
Question 11.
The density of a material in CGS system of units is 4 g cm-3. In a system of units in which unit of length is 10 cm and unit of mass is 100 g, then the value of density of material will be ……
(a) 0.04
(b) 0.4
(c) 40
(d) 400
Answer:
(c) 40
Question 12.
If the force is proportional to square of velocity, then the dimension of proportionality constant
is [JEE-2000] ……
(a) [MLT0]
(b) [MLT-1]
(c) [ML-2T]
(d) [ML-1T0]
Answer:
(d) [ML-1T0]
![]()
Question 13.
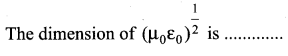 [MainAIPMT2011]
[MainAIPMT2011]
(a) length
(b) time
(c) velocity
(d) force
Answer:
(c) velocity
Question 14.
Planck’s constant (h), speed of light in vaccum (c) and Newton’s gravitational constant (G) are taken as three fundamental constants. Which of the following combinations of these has the dimension of length? [NEET 2016 (Phase II)]

Answer:
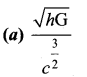
Question 15.
A length-scale (l) depends on the permittivity (ε) of a dielectric material, Boltzmann constant (kB), the absolute temperature (T), the number per unit volume (n) of certain charged particles, and the charge (q) carried by each of the particles. Which of the following expression for l is dimensionally correct?. [JEE (advanced) 2016]
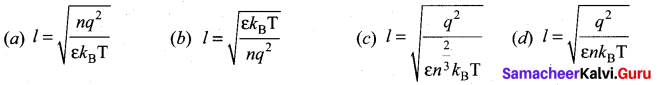
Answer:
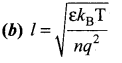
Samacheer Kalvi 11th Physics Nature of Physical World and Measurement Short Answer Questions
Question 1.
Briefly explain the types of physical quantities.
Answer:
Physical quantities are classified into two types. There are fundamental and derived quantities. Fundamental or base quantities are quantities which cannot be expressed in terms of any other physical quantities. These are length, mass, time, electric current, temperature, luminous intensity and amount of substance.
Quantities that can be expressed in terms of fundamental quantities are called derived quantities. For example, area, volume, velocity, acceleration, force.
Question 2.
How will you measure the diameter of the Moon using parallax method?
Answer:
Let θ is the angular diameter of moon
d – is the distance of moon from earth, from figure, θ = \(\frac{\mathrm{D}}{d}\)
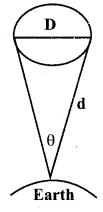
Diameter of moon D = d.θ
by knowing θ, d, diameter of moon can be calculated
Question 3.
Write the rules for determining significant figures.
Answer:
Rules for counting significant figures:
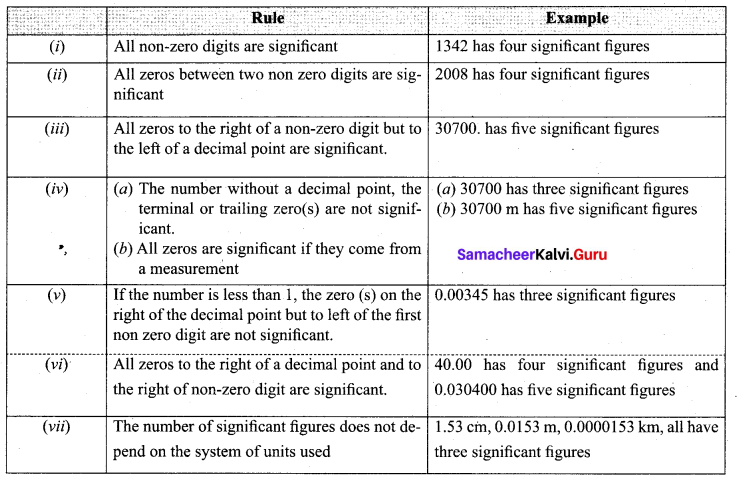
Note: 1 Multiplying or dividing factors, which are neither rounded numbers nor numbers representing measured values, are exact and they have infinite numbers of significant figures as per the situation.
For example, circumference of circle S = 2πr, Here the factor 2 is exact number. It can be written as 2.0, 2.00 or 2.000 as required.
Note: 2 The power of 10 is irrelevant to the determination of significant figures.
For example x = 5.70 m = 5.70 × 102 cm = 5.70 × 103 mm = 5.70 × 10-3 km.
In each case the number of significant figures is three.
Question 4.
What are the limitations of dimensional analysis?
Answer:
Limitations of Dimensional analysis
1. This method gives no information about the dimensionless constants in the formula like 1, 2, ……… π, e, etc.
This method cannot decide whether the given quantity is a vector or a scalar.
This method is not suitable to derive relations involving trigonometric, exponential and logarithmic functions.
It cannot be applied to an equation involving more than three physical quantities.
It can only check on whether a physical relation is dimensionally correct but not the correctness of the relation. For example, using dimensional analysis, 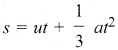 is dimensionally correct whereas the correct relation is
is dimensionally correct whereas the correct relation is 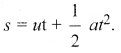
![]()
Question 5.
Define precision and accuracy. Explain with one example.
Answer:
The accuracy of a measurement is a measure of how close the measured value is to the true value of the quantity. Precision of a measurement is a closeness of two or more measured values to each other.
The true value of a certain length is near 5.678 cm. In one experiment, using a measuring instrument of resolution 0.1 cm, the measured value is found to be 5.5 cm. In another experiment using a measuring instrument of greater resolution, say 0.01 cm, the length is found to be 5.38 cm. We find that the first measurement is more accurate as it is closer to the true value, but it has lesser precision. On the contrary, the second measurement is less accurate, but it is more precise.
Samacheer Kalvi 11th Physics Nature of Physical World and Measurement Long Answer Questions
Question 1.
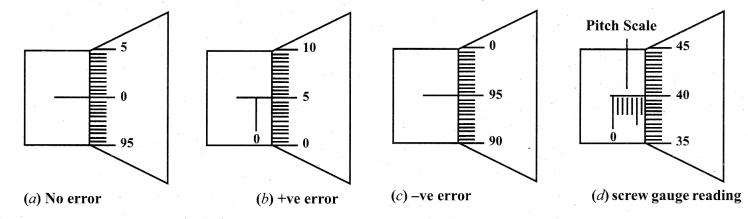
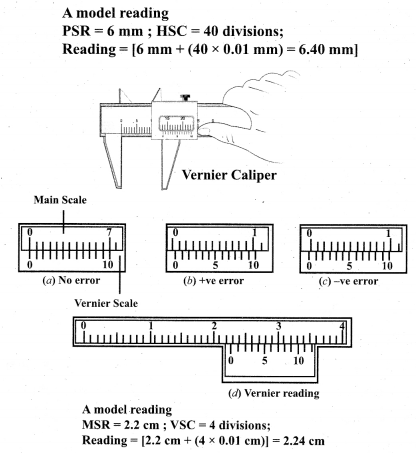
(i) Explain the use of screw gauge and vernier caliper in measuring smaller distances.
Answer:
(i) Measurement of small distances: screw gauge and vernier caliper Screw gauge:
The screw gauge is an instrument used for measuring accurately the dimensions of objects up to a maximum of about 50 mm. The principle of the instrument is the magnification of linear motion using the circular motion of a screw. The least count of the screw gauge is 0.01 mm. Vernier caliper: A vernier caliper is a versatile instrument for measuring the dimensions of an object namely diameter of a hole, or a depth of a hole. The least count of the vernier caliper is 0.1 mm.

(ii) Write a note on triangulation method and radar method to measure larger distances. Triangulation method for the height of an accessible object;
Let AB = h be the height of the tree or tower to be measured. Let C be the point of observation at distance x from B. Place a range finder at C and measure the angle of elevation, ACB =
θ as shown in figure.
From right angled triangle ABC,
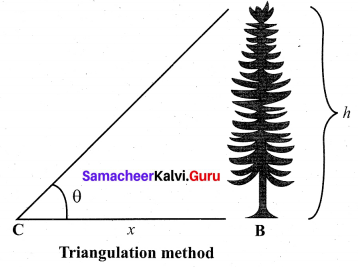
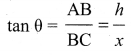
(or) height h = x tan θ
Knowing the distance x, the height h can be determined.
RADAR method
The word RADAR stands for radio detection and ranging. A radar can be used to measure accurately the distance of a nearby planet such as Mars. In this method, radio waves are sent from transmitters which, after reflection from the planet, are detected by the receiver. By measuring, the time interval (t) between the instants the radio waves are sent and received, the distance of the planet can be determined as where v is the speed of the radio wave. As the time taken (t) is for the distance covered during the forward and backward path of the radio waves, it is divided by 2 to get the actual distance of the object. This method can also be used to determine the height, at which an aeroplane flies from the ground.

Question 2.
Explain in detail the various types of errors.
Answer:
The uncertainty in a measurement is called an error. Random error, systematic error and gross error are the three possible errors.
(i) Systematic errors: Systematic errors are reproducible inaccuracies that are consistently *, in the same direction. These occur often due to a problem that persists throughout the experiment. Systematic errors can be classified as follows
(1) Instrumental errors: When an instrument is not calibrated properly at the time of manufacture, instrumental errors may arise. If a measurement is made with a meter scale whose end is worn out, the result obtained will have errors. These errors can be corrected by choosing the instrument carefully.
(2) Imperfections in experimental technique or procedure: These errors arise due to the limitations in the experimental arrangement. As an example, while performing experiments with a calorimeter, if there is no proper insulation, there will be radiation losses. This results in errors and to overcome these, necessary correction has to be applied
(3) Personal errors: These errors are due to individuals performing the experiment, may be due to incorrect initial setting up of the experiment or carelessness of the individual making the observation due to improper precautions.
(4) Errors due to external causes: The change in the external conditions during an experiment can cause error in measurement. For example, changes in temperature, humidity, or pressure during measurements may affect the result of the measurement.
(5) Least count error: Least count is the smallest value that can be measured by the measuring instrument, and the error due to this measurement is least count error. The instrument’s
resolution hence is the cause of this error. Least count error can be reduced by using a high precision instrument for the measurement.
(ii) Random errors: Random errors may arise due to random and unpredictable variations in
experimental conditions like pressure, temperature, voltage supply etc. Errors may also be due to personal errors by the observer who performs the experiment. Random errors are sometimes called “chance error”. When different readings are obtained by a person every time he repeats the experiment, personal error occurs. For example, consider the case of the thickness of a wire measured using a screw gauge. The readings taken may be different for different trials. In this case, a large number of measurements are made and then the arithmetic mean is taken.
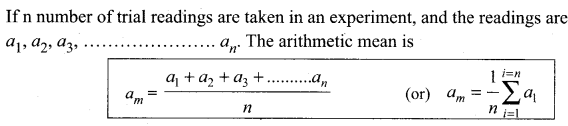
Question 3.
What do you mean by propagation of errors? Explain the propagation of errors in addition and multiplication.
Answer:
A number of measured quantities may be involved in the final calculation of an experiment. Different types of instruments might have been used for taking readings. Then we may have to look at the errors in measuring various quantities, collectively.
The error in the final result depends on
(i) The errors in the individual measurements
(ii) On the nature of mathematical operations performed to get the final result. So we should know the rules to combine the errors.
The various possibilities of the propagation or combination of errors in different mathematical operations are discussed below:
(i) Error in the sum of two quantities
Let ∆A and ∆B be the absolute errors in the two quantities A and B respectively. Then, Measured value of A = A ± ∆A
Measured value of B = B ± ∆B
Consider the sum, Z = A + B
The error ∆Z in Z is then given by

The maximum possible error in the sum of two quantities is equal to the sum of the absolute errors in the individual quantities.
Error in the product of two quantities: Let ∆A and ∆B be the absolute errors in the two quantities A, and B, respectively. Consider the product Z = AB
The error ∆Z in Z is given by Z ± ∆Z = (A ± ∆A) (B ± ∆B)
= (AB) ± (A ∆ B) ± (B ∆ A) ± (∆A • ∆B)
Dividing L.H.S by Z and R.H.S by AB, we get,
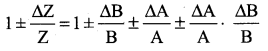
As ∆A/A, ∆B/B are both small quantities, their product term 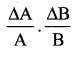 can be neglected.
can be neglected.
The maximum fractional error in Z is
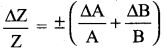
![]()
Question 4.
Write short note on the following:
(a) Unit
(b) Rounding – off
(c) Dimensionless quantities
Answer:
(a) Unit: An arbitrarily chosen standard of measurement of a quantity, which is accepted internationally is called unit of the quantity.
The units in which the fundamental quantities are measured are called fundamental or base units and the units of measurement of all other physical quantities, which can be obtained by a suitable multiplication or division of powers of fundamental units, are called derived units.
(b) Rounding – off: In no case should the result have more significant figures than die figures involved in the data used for calculation. The result of calculation with numbers containing more than one uncertain digit should be rounded off. The rules for rounding off are given below.

(c) Dimensionless quantities: On the basis of dimension, dimensionless quantities are classified into two categories.
(i) Dimensionless variables:
Physical quantities which have no dimensions, but have variable values are called dimensionless variables. Examples are specific gravity, strain, refractive index etc.
(ii) Dimensionless Constant:
Quantities which have constant values and also have no dimensions are called dimensionless constants. Examples are π, e, numbers etc.
Question 5.
Explain the principle of homogeniety of dimensions. What are its uses? Give example.
Answer:
The principle of homogeneity of dimensions states that the dimensions of all the terms in a physical expression should be the same. For example, in the physical expression v2 = u2 + 2as, the dimensions of v2, u2 and 2 as are the same and equal to [L2T-2].
(i) To convert a physical quantity from one system of units to another: This is based on the fact that the product of the numerical values (n) and its corresponding unit (u) is a constant, i.e, = constant n1[u1] = constant (or) n1[u1] = n2[u2].
Consider a physical quantity which has dimension ‘a’ in mass, ‘b’ in length and ‘c’ in time. If the fundamental units in one system are M1, L1 and T1 and the other system are M2, L2 and T2 respectively, then we can write, ![]()
We have thus converted the numerical value of physical quantity from one system of units into the other system.
Example: Convert 76 cm of mercury pressure into Nm-2 using the method of dimensions. Solution: In cgs system 76 cm of mercury pressure = 76 × 13.6 × 980 dyne cm-2
The dimensional formula of pressure P is [ML-1T-2]
(ii) To check the dimensional correctness of a given physical equation:
Example: The equation \(\frac{1}{2} m v^{2}\) = mgh can be checked by using this method as follows.
Solution: Dimensional formula for
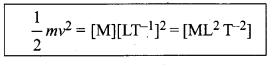
Dimensional formula for
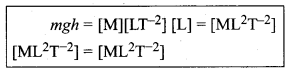
Both sides are dimensionally the same, hence the equations 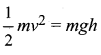 is dimensionally correct.
is dimensionally correct.
(iii) To establish the relation among various physical quantities:
Example: An expression for the time period T of a simple pendulum can be obtained by using this method as follows.
Let true period T depend upon
(i) mass m of the bob
(ii) length l of the pendulum and
(iii) acceleration due to gravity g at the place where the pendulum is suspended. Let the constant involved is K = 2π.
Solution:
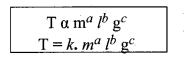
Here k is the dimensionless constant. Rewriting the above equation with dimensions.
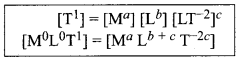
Comparing the powers of M, L and T on both sides, a – 0, b + c = 0, -2c = 1
Solving for a, b and c a = 0, b = 1/2, and c = -1/2
From the above equation

Samacheer Kalvi 11th Physics Nature of Physical World and Measurement Numerical Problems
Question 1.
In a submarine equipped with sonar, the time delay between the generation of a pulse and its echo after reflection from an enemy submarine is observed to be 80 sec. If the speed of sound in water is 1460 ms-1. What is the distance of enemy submarine?
Answer:
Given:
Speed of sound in water = 1460 ms-1
Time delay = 80s
Distance of enemy ship = ?
Solution:
Total distance covered = speed × time
= 1460 ms-1 × 80s = 116800 m
Time taken is for forward and backward path of sound waves.
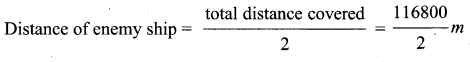
= 58400 m (or) 58.4 km
![]()
Question 2.
The radius of the circle is 3.12 m. Calculate the area of the circle with regard to significant figures.
Answer:
Given: radius : 3.12 m (Three significant figures)
Solution:
Area of the circle = πr2 = 3.14 × (3.12 m)2 = 30.566
If the result is rounded off into three significant figure, area of the circle = 30.6 m2
Question 3.
Assuming that the frequency v of a vibrating string may depend upon
(i) applied force (F)
(ii) length (l)
(iii) mass per unit length (m), prove that 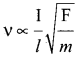 using dimensional analysis. [Related to JIPMER 2001]
using dimensional analysis. [Related to JIPMER 2001]
Answer:
Given: The frequency v of a vibrating string depends
(i) applied force (F)
(ii) length (l)
(iii) mass per unit length (m)
Solution:
![]()
Substitute the dimensional formulae of the above quantities
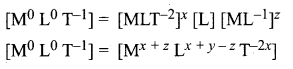
Comparing the powers of M, L, T on both sides,
x + z = 0, x + y – z = 0, -2x = -1
Solving for x, y, z, we get
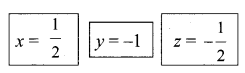
Substitute x, y, z values in equ(1)
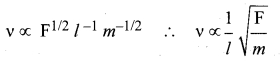
Question 4.
Jupiter is at a distance of 824.7 million km from the Earth. Its angular diameter is measured to be 35.72″. Calculate the diameter of Jupiter.
Answer:
Given,
Given Distance of Jupiter = 824.7 × 106 km = 8.247 × 1011 m
angular diameter = 35.72 × 4.85 × 10-6rad = 173.242 × 10-6 rad
= 1.73 × 10-4 rad
∴ Diameter of Jupiter D = D × d = 1.73 × 10-4 rad × 8.247 × 1011 m
= 14.267 × 1o7 m = 1.427 × 108 m (or) 1.427 × 105</sup km
Question 5.
The measurement value of length of a simple pendulum is 20 cm known with 2 mm accuracy. The time for 50 oscillations was measured to be 40 s within 1 s resolution. Calculate the percentage of accuracy in the determination of acceleration due to gravity ‘g’ from the above measurement.
Answer:
Given,
Length of simple pendulum (l) = 20 cm
absolute error in length (∆l) = 2 mm = 0.2 cm
Time taken for 50 oscillation (t) = 40 s
error in time ∆T = 1 s
Solution: Time period for one oscillation (T)

Hence, the percentage error in g is
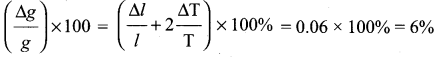
Samacheer Kalvi 11th Physics Nature of Physical World and Measurement Conceptual Questions
Question 1.
Why is it convenient to express the distance of stars in terms of light year (or) parsec rather than in km?
Answer:
A parsec is 206, 265 AU and is roughly the distance to the nearest stars. If we were to view a giant star with a diameter of 1 AU at a distance of one parsec, it would appear to be just 1/3600th of a degree in angular size. For comparison, the sun and moon are both half a degree in angular size when viewed from Earth.
Question 2.
Show that a screw gauge of pitch 1 mm and 100 divisions is more precise than a vernier caliper with 20 divisions on the sliding scale.
Answer:

As shown, the least count of screw gauge is lesser then vernier caliper, hence screw gauge is more precise.
![]()
Question 4.
Having all units in atomic standards is more useful. Explain.
Answer:
An atomic mass unit (symbolized AMU or amu) is defined as precisely 1/12 the mass of an atom of carbon-12. The carbon-12 (C-12) atom has six protons and six neutrons in its nucleus.
In imprecise terms, one AMU is the average of the proton rest mass and the neutron rest mass. This is approximately 1.67377 × 10-27 kilogram (kg), or 1.67377 × 10-24 gram (g). The mass of an atom in AMU is roughly equal to the sum of the number of protons and neutrons in the nucleus.
The AMU is used to express the relative masses of, and thereby differentiate between, various isotopes of elements. Thus, for example, uranium-235 (U-235) has an AMU of approximately 235, while uranium-238 (U-238) is slightly more massive. The difference results from the fact that U-238, the most abundant naturally occurring isotope of uranium, has three more neutrons than U-235, an isotope that has been used in nuclear reactors and atomic bombs.
Question 5.
Why dimensional methods are applicable only up to three quantities?
Answer:
Understanding dimensions is of utmost importance as it helps us in studying the nature of physical quantities mathematically. The basic concept of dimensions is that we can add or subtract only those quantities which have same dimensions. Also, two physical quantities are equal if they have same dimensions. these basic ideas help us in deriving the new relation between physical quantities, it is just like units.
Samacheer Kalvi 11th Physics Nature of Physical World and Measurement Additional Questions Solved
Samacheer Kalvi 11th Physics Nature of Physical World and Measurement Multiple Choose Questions
Question 1.
The unit of surface tension ……
(a) MT-2
(b) Nm-2
(c) Nm
(d) Nm-1
Answer:
(d) Nm-1
Question 2.
One atomus equal to ……

Answer:
(c) 160 ms
Question 3.
One light year is ……
(a) 3.153 × 107 m
(b) 1.496 × 107 m
(c) 9.46 × 1012 km
(d) 3.26 × 1015 km
Answer:
(c) 9.46 × 1012 km
Question 4.
One Astronomical unit is
(a) 3.153 × 107 m
(b) 1.496 × 107 m
(c) 9.46 × 1012 m
(d) 3.26 × 1015 m
Answer:
(b) 1.496 × 107 m
![]()
Question 5.
One parsec is …..
(a) 3.153 × 107 m
(b) 3.26 × 1015 m
(c) 30.84 × 1015 m
(d) 9.46 × 1015 m
Answer:
(c) 30.84 × 1015 m
Question 6.
One Fermi is …..
(a) 10-9 m
(b) 10-10 m
(c) 10-12 m
(d) 10-15 m
Answer:
(d) 10-15 m
Question 7.
One Angstrom is ………
(a) 10-9 m
(b) 10-10m
(c) 10-12 m
(d) 10-15 m
Answer:
(b) 10-10 m
Question 8.
One solar mass is ….
(a) 2 × 1030 kg
(b) 2 × 1030 g
(c) 2 × 1030 mg
(d) 2 × 1030 tonne
Answer:
(d) 2 × 1030 tonne
![]()
Question 9.
\(\frac{1}{12}\) of the mass of carbon 12 atom is …..
(a) 1 TMC
(b) mass of neutron
(c) 1 amu
(d) mass of hydrogen
Answer:
(d) mass of hydrogen
Question 10.
The word physics is derived from the word …..
(a) scientist
(b) fusis
(c) fission
(d) fusion
Answer:
(b) fusis
Question 11.
The study of forces acting on bodies whether at rest or in motion is …..
(a) classical mechanics
(b) quantum mechanics
(c) thermodynamics
(d) condensed matter physics
Answer:
(a) classical mechanics
Question 12.
Mass of observable universe …..
(a) 1031 kg
(b) 1041 kg
(c) 1055 kg
(d) 9.11 × 1031 kg
Answer:
(c) 1055 kg
Question 13.
Mass of an electron …….
![]()
Answer:
(b) 9.11 × 10-31 kg
Question 14.
The study of production and propagation of sound waves …..
(a) Astrophysics
(b) Acoustics
(c) Relativity
(d) Atomic physics
Answer:
(b) Acoustics
![]()
Question 15.
The study of the discrete nature of phenomena at the atomic and subatomic levels.
(a) Quantum mechanics
(b) High energy physics
(c) Acoustics
(d) Classical mechanics
Answer:
(a) Quantum mechanics
Question 16.
The techniQuestion used to study the crystal structure of various rocks are …….
(a) diffraction
(b) interference
(c) total internal reflection
(d) refraction
Answer:
(a) diffraction
Question 17.
The astronomers used to observe distant points of the universe by …….
(a) Electron telescope
(b) Astronomical telescope
(c) Radio telescope
(d) Radar
Answer:
(c) Radio telescope
Question 18.
The comparison of any physical quantity with its standard unit is known as ……..
(a) fundamental quantities
(b) measurement
(c) dualism
(d) derived quantities
Answer:
(b) measurement
Question 19.
Fundamental quantities can also be known as …… quantities.
(a) original
(b) physical
(c) negative
(d) base
Answer:
(d) base
![]()
Question 20.
Which one of the following is not a fundamental quantity?
(a) length
(b) luminous intensity
(c) temperature
(d) water current
Answer:
(d) water current
Question 21.
The system of unit not only based on length, mass, and time is
(a) FPS
(b) CGS
(c) MKS
(d) SI
Answer:
(d) SI
Question 22.
The coherent system of units …..
(a) CGS
(b) SI
(c) FPS
(d) MKS
Answer
(b) SI
Question 23.
The triple point temperature of water is ……
(a) -273.16 K
(b) 0K
(c) 273.16 K
(d) 100 K
Answer:
(d) 100 K
Question 24.
Which of the following is a unit of distance?
(a) Light year
(b) Leap year
(c) Dyne-sec
(d) Pauli
Answer:
(a) Light year
Question 25.
The unit of moment of force ……
(a) Nm2
(b) Nm
(c) N
(d) NJ rad
Answer:
(b) Nm
![]()
Question 26.
1 radian is ……
(a) 2.91 × 10-4 m
(b) 57.27°
(c) 180°
(d) \(\frac{\pi}{180}\)
Answer:
(b) 57.27°
Question 27.
One degree of arc is …….
(a) 1″
(b) 60″
(c) 60′
(d) 60°
Answer:
(c) 60′
Question 28.
One degree of arc is equal to …….
(a) 1.457 × 102 rad
(b) 1.457 × 10-2 rad
(c) 1.745 × 102 rad
(d) 1.745 × 10-2 rad
Answer:
(b) 1.457 × 10-2 rad
Question 29.
1 minute of arc is equal to …….
(a) 1.745 × 10-2 rad
(b) 2.91 × 10-4 rad
(c) 2.91 × 104 rad
(d) 4.85 × 10-6 rad
Answer:
(b) 2.91 × 10-4 rad
Question 30.
1 second of arc is equal to ………

Answer:
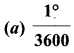
Question 31.
1 second of arc is equal to ….
(a) 0.00027°
(b) 1.745 × 10-2 rad
(c) 2.91 × 10-4 rad
(d) 4.85 × 10-6 rad
Answer:
(a) 0.00027°
Question 32.
Unit of impulse ….
(a) NS2
(b) NS
(c) Nm
(d) Kgms-2
Answer:
(b) NS
Question 33.
The ratio of energy and temperature is known as ……
(a) Stefen’s constant
(b) Boltzmann constant
(c) Plank’s constant
(d) Kinetic constant
Answer:
(b) Boltzmann constant
Question 34.
The range of distance can be measured by using direct methods is …..
(a) 10-2 to 10-5 m
(b) 10-2 to 102 m
(c) 102 to 1(T5 m {d) 10″2 to 105 m
Answer:
(b) 10-2 to 102 m
Question 35.
Which of the following is in increased order?
(a) exa, tera, hecto
(b) tera, exa, hecto
(c) giga, tera, exa
(d) hecto, exa, giga
Answer:
(c) giga, tera, exa
Question 36.
10-18 is called as ……
(a) nano
(b) pico
(c) femto
(d) atto
Answer:
(d) atto
![]()
Question 37.
A radio signal sent towards the distant planet, returns after “t” s. If “c” is the speed of radio
waves then the distance of the planet and from the earth is …….

Answer:
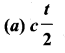
Question 38.
Find odd one out ….
(a) Newton
(b) metre
(c) candela
(d) Kelvin
Answer:
(a) Newton
Question 39.
The shift in the position of an object when viewed with two eyes, keeping one eye closed at a
time is known as …
(a) basis
(b) fundamental
(c) parallax
(d) pendulum
Answer:
(c) parallax
Question 40.
Chandrasekar limit is ….. times the mass of the sun.
(a) 1.2
(b) 1.4
(c) 1.6
(d) 1.8
Answer:
(b) 1.4
Question 41.
The smallest physical unit of time is
(a) second
(b) minute
(c) microsecond
(d) shake
Answer:
(d) shake
Question 42.
Size of atomic nucleus is …..
(a) 10-10 m
(b) 10-12 m
(c) 10-14 m
(d) 10-18 m
Answer:
(c) 10-14 m
![]()
Question 43.
Time interval between two successive heart beat is in the order of …….
(a) 10° s
(b) 10 s
(c) 102 s
(d) 10-3 s
Answer:
(a) 10° s
Question 44.
Half life time of a free neutron is in the order of ……
(a) 10°
(b) 101 s
(c) 102 s
(d) 103 s
Answer:
(d) 103 s
Question 45.
The uncertainty contained in any measurement is ……
(a) rounding off
(b) error
(c) parallax
(d) gross
Answer:
(b) error
Question 46.
Zero error of an instrument is a ……
(a) Systematic error
(b) Random error
(c) Gross error
(d) Both (a) and (b)
Answer:
(a) Systematic error
Question 47.
Error in the measurement of radius of a sphere is 2%. Then error in the measurement of surface
area is ….
(a) 1%
(b) 2%
(c) 3%
(d) 4%
Answer:
(d) 4%
![]()
Question 48.
Imperfections in experimental procedure gives ….. error.
(a) random
(b) gross
(c) systematic
(d) personal
Answer:
(c) Systematic
Question 49.
Random error can also be called as ….
(a) personal error
(b) chance error
(c) gross error
(d) system error
Answer:
(b) chance error
Question 50.
To get the best possible true value of the quantity has to be taken.
(a) rms value
(b) net value
(c) arithmetic mean
(d) mode
Answer:
(c) arithmetic mean
Question 51.
The error caused due to the shear carelessness of an observer is called as …… error.
(a) Systematise
(b) Gross
(c) Random
(d) Personal
Answer:
(b) Gross
Question 52.
The uncertainty in a measurement is called as ….
(a) error
(b) systematic
(c) random error
(d) gross error
Answer:
(a) error
Question 53.
The difference between the true value and the measured value of a quantity is known as …..
(a) Absolute error
(b) Relative error
(c) Percentage error
(d) Systemmatic error
Answer:
(a) Absolute error
Question 54.
If a1, a2, a3 …. an are the measured value of a physical quantity “a” and am is the true value then absolute error …..
![]()
Answer:
(d) \(\Delta a_{n}=a_{m}-a_{n}\)
Question 55.
If ‘am‘ and ‘∆am ‘ are true value and mean absolute error respectively, then the magnitude of the quantity may lie between …..

Answer:
(b) \(a_{m}-\Delta a_{m} \text { to } a_{m}+\Delta a_{m}\)
Question 56.
The ratio of the mean absolute error to the mean value is called as ……
(a) absolute error
(b) random error
(c) relative error
(d) percentage error
Answer:
(c) Relative error
Question 57.
Relative error can also be called as ……
(a) fractional error
(b) absolute error
(c) percentage error
(d) systematic error
Answer:
(a) fractional error
Question 58.
A measured value to be close to targeted value, percentage error must be close to
(a) 0
(b) 10
(c) 100
(d) ∝
Answer:
(a) 0
Question 59.
The maximum possible error in the sum of two quantities is equal to …….
(a) Z = A + B
(b) ∆Z = ∆A + ∆B
(c) ∆Z = ∆A/∆B
(d) ∆Z = ∆A – ∆B
Answer:
(b) ∆Z = ∆A + ∆B
Question 60.
The maximum possible error in the difference of two quantities is ……
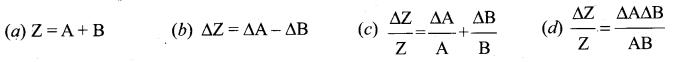
Answer:
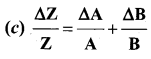
Question 61.
The maximum fractional error in the division of two quantities is ….
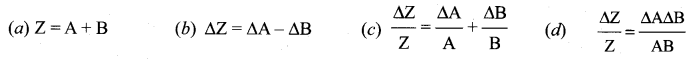
Answer:
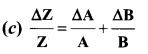
Question 62.
The fractional error in the nth power of a quantity is …..

Answer:
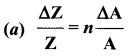
Question 63.
A physical quantity is given as y = \(\frac{a b^{3}}{c^{2}}\). If ∆a, ∆b, ∆c are absolute errors, the possible fractional error in y is …..

Answer:
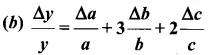
Question 64.
Number of significant digits in 3256 …
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(d) 4
Question 65.
Number of significant digits in 32005 ……
(a) 1
(b) 2
(c) 5
(d) 2
Answer:
(c) 5
![]()
Question 66.
Number of significant digits in 2030 …
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(d) 4
Question 67.
Number of significant digits in 2030N …..
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(d) 4
Question 68.
Number of significant digits in 0.0342 …..
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(c)3
Question 69.
Number of significant digit in 20.00 …..
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(d) 4
Question 70.
Number of significant digit in 0.030400
(a) 6
(b) 5
(c) 4
(d) 3
Answer:
(b) 5
Question 71.
The force acting on a body is measured as 4.25 N. Round it off with two significant figure ..
(a) 4.3
(b) 4.2
(c) both
(a) or (b)
(d) 4.25
Answer:
(b) 4.2
Question 72.
The quantities a, b, c are measured as 3.21, 4.253, 7.2346. The sum (a + b + c) with proper
significant digits is ……
(a) 14.6976
(b) 14.697
(c) 14.69
(d) 14.6
Answer:
(c) 14.69
Question 73.
The dimensions of gravitational constant G are …
![]()
Answer:
(b) \(\mathbf{M}^{-1} \mathbf{L}^{3} \mathbf{T}^{-2}\)
Question 74.
The ratio of one nanometer to one micron is
(a) 10-3
(b) 103
(c) 10-9
(d) 10-6
Answer:
(b) 103
Question 75.
Which of the following pairs does not have same dimension?
(a) Moment of inertia and moment of force
(b) Work and torque
(c) Impulse and momentum
(d) Angular momentum and Plank’s constant
Answer:
(a) Moment of inertia and moment of force
Question 76.
Two quantities A and B have different dimensions. Which of the following is physically meaningful?
(a) A + B
(b) A – B
(c) A /B
(d) None
Answer:
(c) A /B
![]()
Question 77.
The dimensional formula for moment of inertia ……
![]()
Answer:
(d) \(\mathbf{M} \mathbf{L}^{2} \mathbf{T}^{\mathbf{0}}\)
Question 78.
Which of the following is having same dimensional formula?
(a) Work and power
(b) Radius of gyration and displacement
(c) Impulse and force
(d) Frequencies and wavelength
Answer:
(b) Radius of gyration and displacement
Question 79.
Which of the following quantities is expressed as force per unit area?
(a) Pressure
(b) Stress
(c) Both (a) and (b)
(d) None
Answer:
(c) Both (a) and (b)
Question 80.
In equation of motion 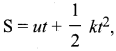 the dimensional formula for K is …..
the dimensional formula for K is …..
![]()
Answer:
(b) \(\left[\mathbf{L} \mathbf{T}^{-2}\right]\)
Question 81.
The dimensional formula for heat capacity ……
![]()
Answer:
(d) \(\left[\mathbf{M} \mathbf{L}^{2} \mathbf{T}^{2} \mathbf{K}^{-1}\right]\)
Question 82.
The product of Avogadro constant and elementary charge is known as …… constant.
(a) Planck’s
(b) Avagadro
(c) Boltzmann
(d) Faraday
Answer:
(d) Faraday
Question 83.
The force F is given by F = at + bt2 where t is time. The dimensions of ‘a’ and ‘b’ respectively are

Answer:
(d) \(\left[\mathrm{MLT}^{-2}\right]\) and \(\left[\mathrm{MLT}^{-0}\right]\)
Question 84.
Dimensions of impulse are …..
![]()
Answer:
(c) \(\left[\mathrm{MLT}^{-1}\right]\)
Question 85.
If speed of light (c), acceleration due to gravity (g) and pressure (P) are taken as fundamental
units, the possible relation to gravitational constant (G) is ….
![]()
Answer:
(c) \(c^{0} g^{2} p^{-1}\)
Question 86.
Equivalent of one joule is ……
(a) Nm2
(b) kg m2 s-2
(c) kg m s-1
(d) N kg m2
Answer:
(b) kg m2 s-2
Question 87.
Pick out the dimensionless quantity …..
(a) force
(b) specific gravity
(c) planck’s constant
(d) velocity
Answer:
(b) specific gravity
Question 88.
Odd one out ………
(a) strain
(b) refractive index
(c) numbers
(d) stress
Answer:
(d) stress
Question 89.
A wire has a mass 0.3 ± 0.003g, radius 0.5 ± 0.005 mm and length 6 + 0.06 cm. The maximum percentage error in the measurement of its density is …….
(a) 1%
(b) 2%
(c) 3%
(d) 4%
Answer:
(d) 4%
![]()
Question 90.
The dimensions of planck constant equals to that of …..
(a) energy
(b) momentum
(c) angular momentum
(d) power
Answer:
(c) angular momentum
Question 91
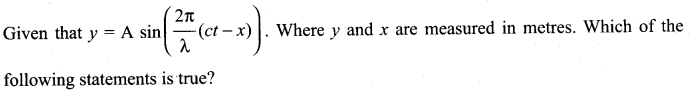
(a) The unit of λ is same as that of x and A
(b) The unit of λ is same as that of x but not of A
(c) The unit of c is same as that of 2π/λ
(d) The unit of (ct – x)is same as that 2π/λ
Answer:
(a) The unit of λ is same as that of x and A
Question 92.
The number of significant figures in 0.06900 is …….
(a) 2
(b) 2
(c) 4
(d) 5
Answer:
(c) 4
Question 93.
The numbers 3.665 and 3.635 on rounding off to 3 significant figures will give
(a) 3.66 and 3.63
(b) 3.66 and 3.64
(c) 3.67 and 3.63
(d) 3.67 and 3.64
Answer:
(b) 3.66 and 3.64
Question 94.
Which of the following measurements is most precise?
(a) 4.00 mm
(b) 4.00 cm
(c) 4.00 m
(d) 4.00 km
Answer:
(a) 4.00 mm
Question 95.
The mean radius of a wire is 2 mm. Which of the following measurements is most accurate? (a) 1.9 mm
(b) 2.25 mm
(c) 2.3 mm
(d) 1.83 mm
Answer:
(a) 1.9 mm
Question 96.
If error in measurement of radius of sphere is 1%. What will be the error in measurement of volume?
(a) 1%
(b) \(\frac{1}{3}\)%
(c) 3%
(d) 10%
Answer:
(c) 3%
Question 97.
Dimensions [M L-1 T-1] are related to …….
(a) torque
(b) work
(c) energy
(d) Coefficient of viscosity
Answer:
(d) Coefficient of viscosity
Question 98.
Heat produced by a current is obtained a relation H = I2RT. If the errors in measuring these quantities current, resistance, time are 1%, 2%, 1% respectively then total error in calculating the energy produced is
(a) 2%
(b) 4%
(c) 5%
(d) 6%
Answer:
(c) 5%
Question 99.
Length cannot be measured by ….
(a) fermi
(b) angstrom
(c) parsec
(d) debye
Answer:
(d) debye
Question 100.
The pressure on a square plate is measured by measuring the force on the plate and the length of the sides of the plate by using the formula p = \([/late\frac{\mathrm{F}}{l^{2}}x]. If the maximum errors in the measurement
of force and length are 4% and 2% respectively, then the maximum error in the measurement of pressure is ……..
(a) 1%
(b) 2%
(c) 8%
(d) 10%
Aswer:
(c) 8%
Question 101.
Which of the following cannot be verified by using dimensional analysis?
1 mv2
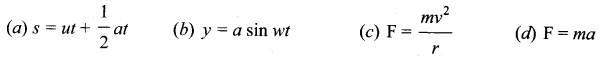
Answer:
(b) y = a sin wt
Question 102.
Percentage errors in the measurement of mass and speed are 3% and 2% respectively. The error in the calculation of kinetic energy is …….
(a) 2%
(b) 3%
(c) 5%
(d) 7%
Answer:
(d) 7%
Question 103.
More number of readings will reduce …….
(a) random error
(b) systematic error
(c) both (a) and (b)
(d) neither (a) nor (b)
Answer:
(a) random error
![]()
Question 104.
If the percentage error in the measurement of mass and momentum of a body are 3% and
2%respectively, then maximum possible error in kinetic energy is
(a) 2%
(b) 3%
(c) 5%
(d) 7%
Answer:
(d) 7%
Question 105.
In a vernier caliper, n divisions of vernier scale coincides with (n – 1) divisions of main scale. The least count of the instrument is ………

Answer:
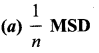
Question 106.
The period of a simple pendulum is recorded as 2.56s, 2.42s, 2.71s and 2.80s respectively.
The average absolute error is
(a) 0.1s
(b) 0.2s
(c) 1.0s
(d) 0.11s
Answer:
(d) 0.11s
Question 107.
In a system of units, if force (F), acceleration (A) and time (T) are taken as fundamental units
then the dimensional formula of energy is
(a) [FA2T]
(b) [FAT2]
(c) [F2AT]
(d) [FAT]
Answer:
(b) [FAT2]
Question 108.
The random error in the arithmetic mean of 50 observations is ‘a’, then the random error in the
arithmetic mean of 200 observations a would be
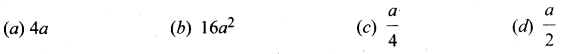
Answer:
(c) [latex]\frac{a}{4}\)
Question 109.
Which of the following is not dimensionless?
(a) Relative permittivity
(b) Refractive index
(c) Relative density
(d) Relative velocity
Answer:
(d) Relative velocity
Question 110.
If V-velocity, K – kinetic energy and T – time are chosen as the fundamental units, then what is the dimensional formula for surface tension?
![]()
Answer:
(a) [K V-2 T-2]
Samacheer Kalvi 11th Physics Nature of Physical World and Measurement Short Answer Questions (1 Mark)
Question 1.
A new unit of length is chosen such that the speed of light in vaccum is unity. What is the distance between the sun and the earth in terms of the new unit if light takes 8 min and 20 s to cover this distance.
Answer:
Speed of light in vacuum, c = 1 new unit of length s-1
t = 8 min. 20 sec, = 500 s
x = ct= 1 new unit of length s-1 × 500s
x = 500 new unit of length
Question 2.
If x = a + bt + ct2, where x is in metre and t in seconds, what is the unit of c ?
Answer:
The unit of left hand side is metre so the units of ct2 should also be metre.
Since t2 has unit of s2, so the unit of c is m/s2.
Question 3.
What is the difference between mN, Nm and nm ?
Answer:
mN means milli newton, 1 mN = 10-3 N, Nm means Newton meter, nm means nano meter.
Question 4.
The radius of atom is of the order of 1 A° & radius of nucleus is of the order of fermi. How many magnitudes higher is the volume of the atom as compared to the volume of nucleus ?
Answer:
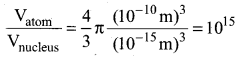
Question 5.
How many kg make 1 unified atomic mass unit ?
Answer:
1u = 1.66 × 10-27 kg
Question 6.
Name some physical quantities that have same dimension.
Answer:
Work, energy and torque.
Question 7.
Name the physical quantities that have dimensional formula [ML -1T-2].
Answer:
Stress, pressure, modulus of elasticity.
Question 8.
Give two examples of dimensionless variables.
Answer:
Strain, refractive index.
![]()
Question 9.
State the number of significant figures in
(i) 0.007 m2
(ii) 2.64 × 1024 kg
(iii) 0.2370 g cm-3
(iv) 0.2300m
(v) 86400
(vi) 86400 m
Answer:
(i) 1,
(ii) 3,
(iii) 4,
(iv) 4,
(v) 3,
(vi) 5 since it comes from a measurement the last two zeros become significant.
Question 10.
Given relative error in the measurement of length is 0.02, what is the percentage error ?
Answer:
2%.
Question 11.
A physical quantity P is related to four observables a, b, c and d as follows :
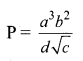
The percentage errors of measurement in a, b, c and d are 1%, 3%, 4% and 2% respectively. What is the percentage error in the quantity P?
Answer:
Relative error in P is given by

Question 12.
A boy recalls the relation for relativistic mass (m) in terms of rest mass (m0) velocity of particle V, but forgets to put the constant c (velocity of light). He writes 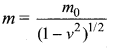 correct the equation by putting the missing ‘c’.
correct the equation by putting the missing ‘c’.
Answer:
Since quantities of similar nature can only be added or subtracted, v2 cannot be subtracted from 1 but v2/c2 can be subtracted from 1.
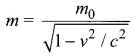
Question 13.
Name the technique used in locating.
(a) an under water obstacle
(b) position of an aeroplane in space.
Answer:
(a) SONAR ➝ Sound Navigation and Ranging.
(b) RADAR ➝ Radio Detection and Ranging.
Question 14.
Deduce dimensional formulae of—
(i) Boltzmann’s constant
(ii) mechanical equivalent of heat.
Answer:
(i) Boltzmann Constant:

![]()
Question 15.
Give examples of dimensional constants and dimensionless constants.
Answer:
Dimensional Constants : Gravitational constant, Plank’s constant. Dimensionless Constants : it, e.
Samacheer Kalvi 11th Physics Nature of Physical World and Measurement Short Answer Questions (2 Marks)
Question 16.
The vernier scale of a travelling microscope has 50 divisions which coincide with 49 main scale divisions. If each main scale division is 0.5 mm. Calculate the minimum inaccuracy in the measurement of distance.
Answer:
Minimum inaccuracy = Vernier constant

Question 17.
If the unit of force is 100N, unit of length is 10m and unit of time is 100s. What is the unit of Mass in this system of units ?
Answer:
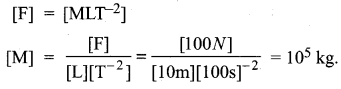
Question 18.
State the principle of homogeneity. Test the dimensional homogeneity of equations
![]()
Answer:
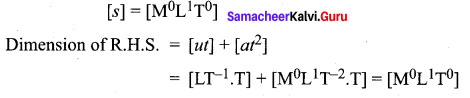
as Dimensions of L.H.S. = Dimensions of R.H.S.
∴ The equation to dimensionally homogeneous.
(ii) Sn = Distance travelled in nth sec that is (Sn – Sn – 1)
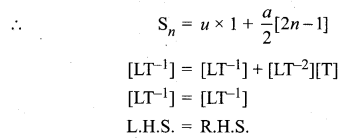
Hence this is dimensionally correct.
Question 19.
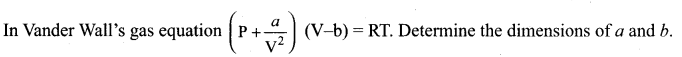
Answer:
Since dimensionally similar quantities can only be added
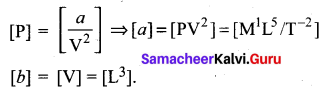
Question 20.
Magnitude of force experienced by an object moving with speed v is given by F = kv2. Find dimensions of k.
Answer:
Question 21.
A book with printing error contains four different formulae for displacement. Choose the
correct formula/formulae
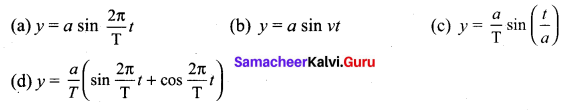
Answer:
The arguments of sine and cosine function must be dimensionless so (a) is the probable correct formulae. Since

Samacheer Kalvi 11th Physics Nature of Physical World and Measurement Numericals Questions
Question 22.
Determine the number of light years in one metre.
Answer:
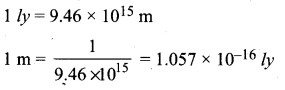
Question 23.
The mass of a box measured by a grocer’s balance is 2.3 kg. Two gold pieces 20.15 g and 20.17 g are added to the box.
(i) What is the total mass of the box ?
(ii) The difference in masses of the pieces to correct significant figures.
Answer:
(i) Mass of box = 2.3 kg
Mass of gold pieces = 20.15 + 20.17 = 40.32 g = 0.04032 kg.
Total mass = 2.3 + 0.04032 = 2.34032 kg
In correct significant figure mass = 2.3 kg (as least decimal)
(ii) Difference in mass of gold pieces = 0.02 g
In correct significant figure (2 significant fig. minimum decimal) will be 0.02 g.
Question 24.
5.74 g of a substance occupies 1.2 cm3. Express its density to correct significant figures.
Answer:
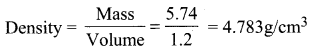
Here least significant figure is 2, so density = 4.8 g/cm3.
Question 25.
If displacement of a body s = (200 ± 5) m and time taken by it t = (20 + 0.2) s, then find the percentage error in the calculation of velocity.
Answer:

Question 26.
If the error in measurement of mass of a body be 3% and in the measurement of velocity be 2%. What will be maximum possible error in calculation of kinetic energy.
Answer:
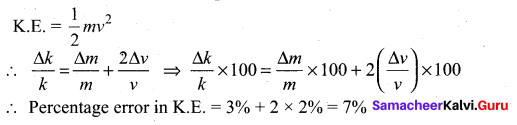
Question 27.
The length of a rod as measured in an experiment was found to be 2.48 m, 2.46 m, 2.49 m, 2.50 m and 2.48 m. Find the average length, absolute error and percentage error. Express the result with error limit.
Answer:

Question 28.
A physical quantity is measured as Q = (2.1 ± 0.5) units. Calculate the percentage error in (1) Q2 (2) 2Q.
Answer:

Question 29.
When the planet Jupiter is at a distance of 824.7 million km from the earth, its angular diameter is measured to be 35.72″ of arc. Calculate diameter of Jupiter.
Answer:

Question 30.
A laser light beamed at the moon takes 2.56s and to return after reflection at the moon’s surface. What will be the radius of lunar orbit?
Answer:
t = 2.54 s
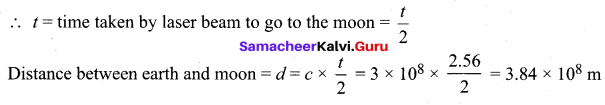
Question 31.
Convert
(i) 3 m.s-2 to km h-2
(ii) G = 6.67 × 10-11 N m2 kg-2 to cm3 g-1 s-2
Answer:

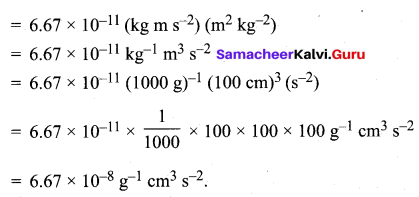
Question 32.
A calorie is a unit of heat or energy and it equals 4.2 J where 1J = 1 kg m2s-2. Suppose we employ a system of units in which unit of mass is α kg, unit of length is β m, unit of time γs. What will be magnitude of calorie in terms of this new system.
Answer:
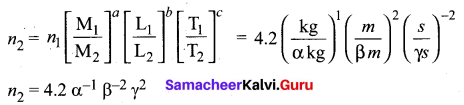
Question 33.
The escape velocity v of a body depends on—
(i) the acceleration due to gravity ‘g’ of the planet,
(ii) the radius R of the planet. Establish dimensionally the relation for the escape velocity.
Solution:

Question 34.
The frequency of vibration of a string depends of on,
(i) tension in the string
(ii) mass per unit length of string,
(iii) vibrating length of the string. Establish dimensionally the relation for frequency.
Answer:

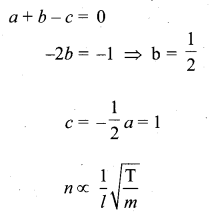
Question 35.
One mole of an ideal gas at STP occupies 22.4 L. What is the ratio of molar volume to atomic volume of a mole of hydrogen? Why is the ratio so large? Take radius of hydrogen molecule to be 1°A.
Answer:
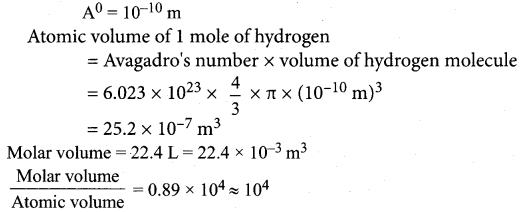
This ratio is large because actual size of gas molecule is negligible in comparison to the inter molecular separation.