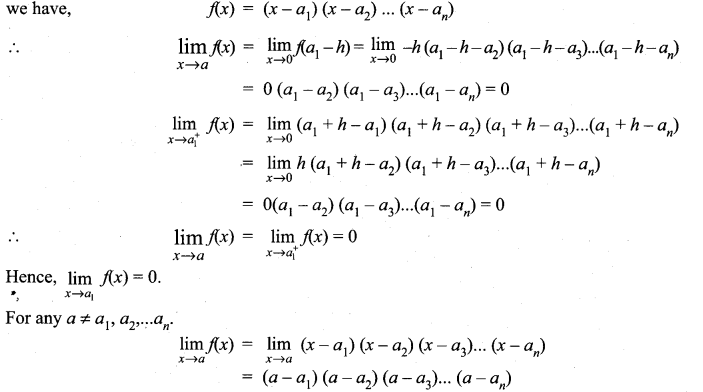Samacheer Kalvi 11th Maths Solutions Chapter 9 Limits and Continuity Ex 9.1

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 9 Limits and Continuity Ex 9.1

In problems 1-6, complete the table using calculate and use the result to estimate the limit.

Question 1.

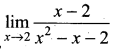
Solution:

Question 2.

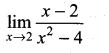
Solution:

∴ Limit is 0.25

Question 3.

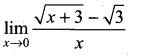
Solution:

∴ Limit is 0.288

Question 4.

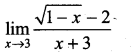
Solution:

∴ Limit is -0.25

Question 5.

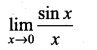
Solution:

∴ Limit is 1

Question 6.

Solution:

∴ Limit is 0

In exercise problems 7-15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?

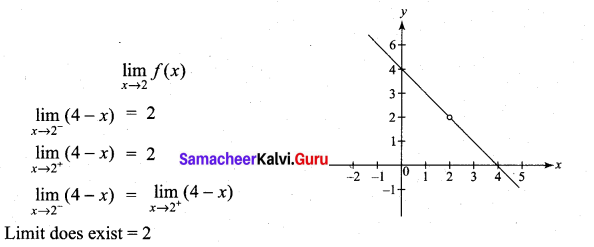
Question 7.
\(\lim _{x \rightarrow 3}\)(4 – x)
Solution:

Limit exists and is equal to 1

Question 8.
\(\lim _{x \rightarrow 1}\)(x² + 2)
Solution:

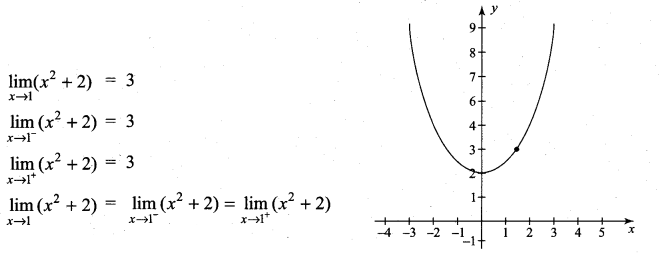
Limit exists and is equal to = 3

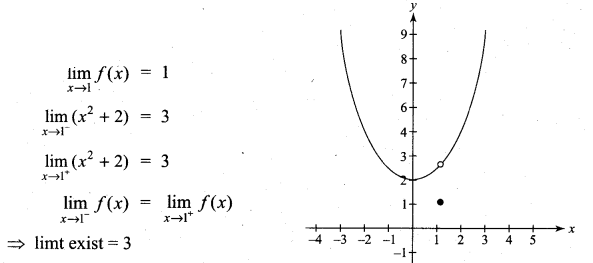
Question 9.

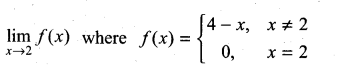
Solution:

Question 10.

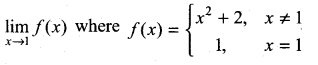
Solution:

Question 11.

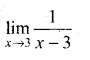
Solution:

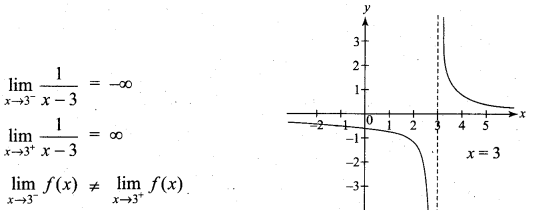
The limit does not exist

Question 12.

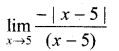
Solution:
When x → 5, (x – 5) = -(x – 5)
∴ \(\lim _{x \rightarrow 5^{-}} \frac{-(x-5)}{(x-5)}\) = -1
When x → 5⁺, (x – 5) = (x – 5)

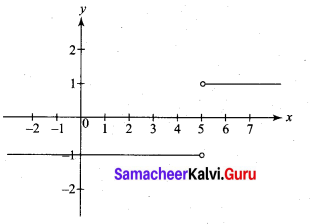
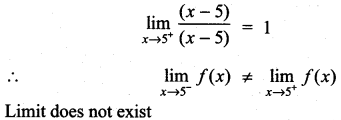
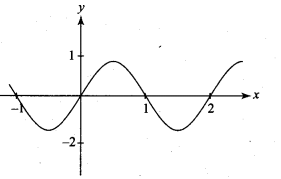
Question 13.
\(\lim _{x \rightarrow 1}\) sin(πx)
Solution:

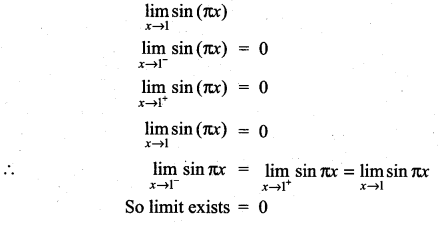
Question 14.
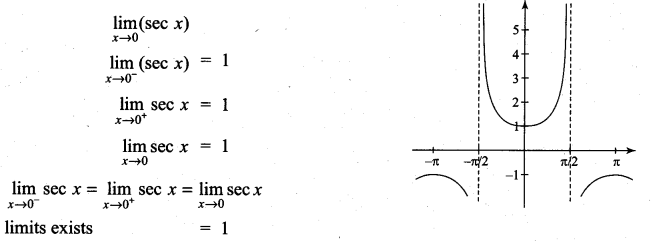
\(\lim _{x \rightarrow 0}\) (sec x)
Solution:

Question 15.
\(\lim _{x \rightarrow \frac{\pi}{2}}\) tan x
Solution:

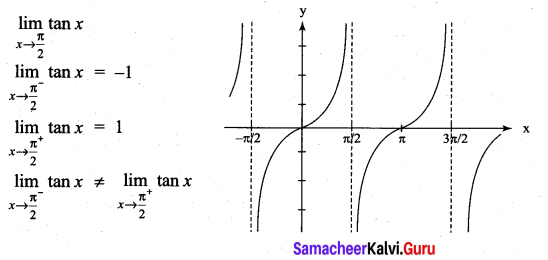
The limit does not exist

Sketch the graph of f, then identify the values of x₀ for which \(\lim _{x \rightarrow x_{0}}\) f(x) exists.

Question 16.

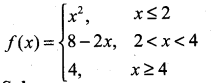
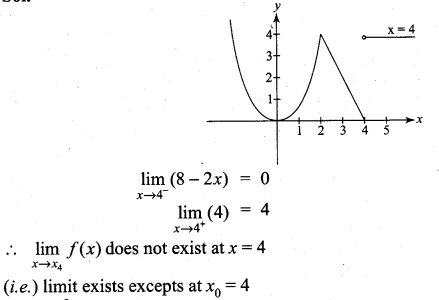
Solution:

Question 17.

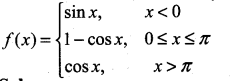
Solution:

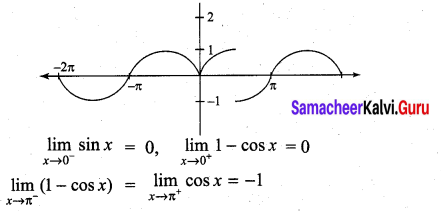
Limit exists except at x₀ = π

Question 18.
Sketch the graph of a function f that satisfies the given values:

Solution:

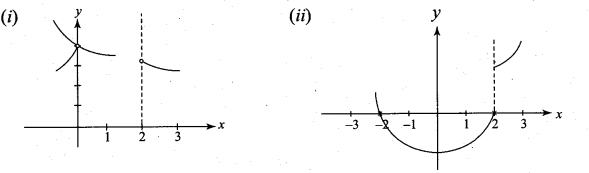
Question 19.
Write a brief description of the meaning of the notation \(\lim _{x \rightarrow 8}\) f(x) = 25
Solution:

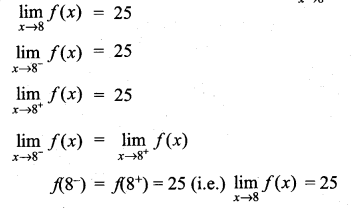
Question 20.
If f(2) = 4, can you conclude anything about the limit of f(x) as x approaches 2?
Solution:
Given f(2) = 4
Here at x = 2 the value of the function is given.
Therefore, we cannot conclude anything about the limit of f(x) as x approaches 2.

Question 21.
If the limit of f(x) as z approaches 2 is 4, can you conclude anything about f(2)?
Explain reasoning.
Solution:
Given \(\lim _{x \rightarrow 2}\) f(x) = 4
Since the limit of the function need not be equal to the value of the function, we cannot conclude anything about f(2).

Question 22.
Evaluate: \(\lim _{x \rightarrow 3} \frac{x^{2}-9}{x-3}\) if it exists by finding f(3^–) and f(3⁺).
Solution:

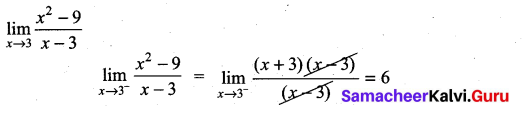
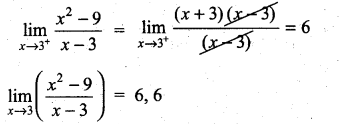
Question 23.
Verify the existence of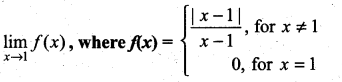
Solution:

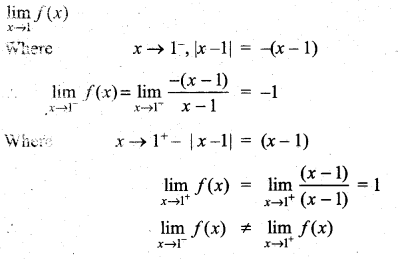
The limit does not exist

Samacheer Kalvi 11th Maths Solutions Chapter 9 Limits and Continuity Ex 9.1 Additional Questions

Question 1.
Suppose 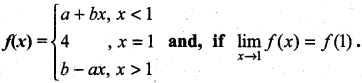. What are the possible values of a and b?
Solution:

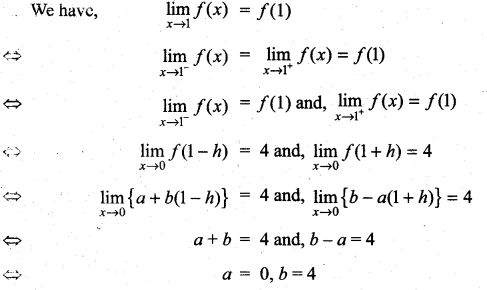
Question 2.

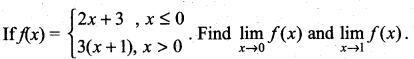
Solution:
We have,

Question 3.

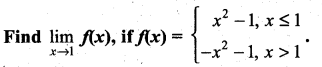
Solution:
We have,

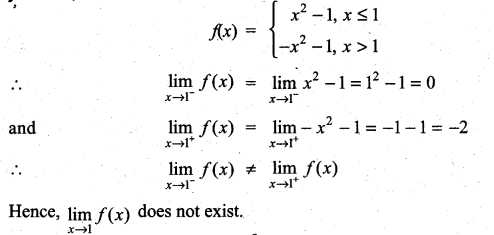
Question 4.

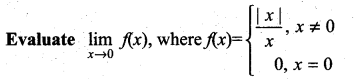
Solution:

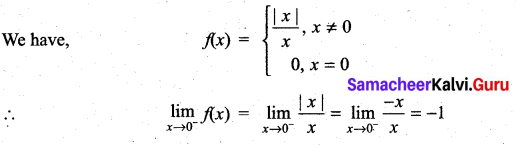
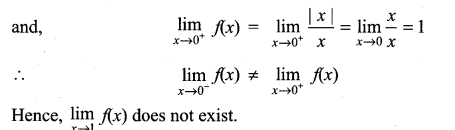
Question 5.
Let a₁, a₂ …………… a_n be fixed real numbers such that f(x) = (x – a₁) , (x – a₂), ………. (x – a_n) what \(\lim _{x \rightarrow a}\) f(x) For a ≠ a₁, a₂, ………… a_n compute \(\lim _{x \rightarrow a}\) f(x).
Solution:
We have,