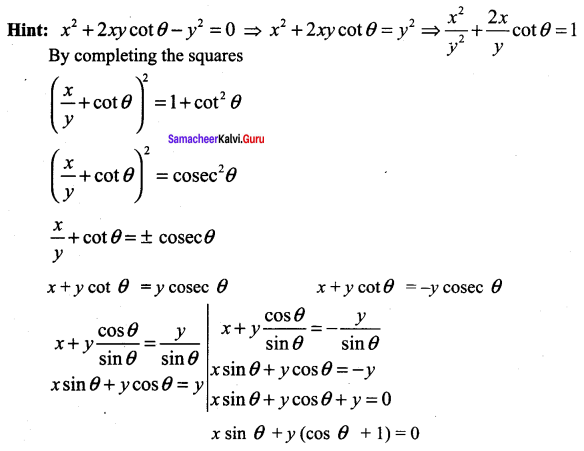Samacheer Kalvi 11th Maths Solutions Chapter 6 Two Dimensional Analytical Geometry Ex 6.5

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 6 Two Dimensional Analytical Geometry Ex 6.5

Choose the correct or more suitable answer

Question 1.
The equation of the locus of the point whose distance from y-axis is half the distance from origin is ……..
(a) x² + 3y² = 0
(b) x² – 3y² = 0
(c) 3x² + y² = 0
(d) 3x² – y² = 0
Solution:
(c) 3x² + y² = 0
Hint:
Given that PA = \([\frac{1}{2}/latex]OP
2PA = OP

4PA² = OP²
4(x)² = x² + y² ⇒ 3x² – y² = 0

Question 2.
Which of the following equation is the locus of (at², 2at) ……

Solution:
(d) y² = 4ax
Hint:
Given x = at², y = 2at
y = 2at ⇒ t = [latex]\frac{y}{2 a}\)
x = at2 ⇒ x = a × \(\left(\frac{y}{2 a}\right)^{2}\)
x = a × \(\frac{y^{2}}{4 a^{2}}\) = \(\frac{y^{2}}{4 a^{2}}\)
y² = 4ax

Question 3.
Which of the following point lie on the locus of 3x² + 3y² – 8x – 12y + 17 = 0?
(a) (0, 0)
(b) (-2, 3)
(c) (1, 2)
(d) (0, -1)
Solution:
(c) (1, 2)
Hint:
The equation of the given locus is
3x² + 3y² – 8x – 12y + 17 = 0
(0, 0) does not lie on the locus since the locus contains constant term. Substituting (-2, 3) in the locus
3(- 2)² + 3(3)² – 8 × – 2 – 12 × 3 + 17
= 3 × 4 + 3 × 9 + 16 – 36 + 17
= 12 + 27 + 16 – 36 + 17 ≠ 0
∴ (- 2, 3) does not lie on the locus
Substituting (1, 2) on the locus
3(1)² + 3(2)² – 8 × 1 – 12 × 2 + 17
= 3 + 12 – 8 – 24 + 17
= 32 – 32
= 0
∴ (1, 2 ) lies on the locus

Question 4.

(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(d) 3

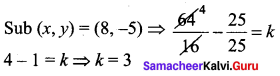
Question 5.
Straight line joining the points (2, 3) and (-1, 4) passes through the point (α, β) if
(a) α + 2β = 7
(b) 3α + β = 9
(c) α + 3β = 11
(d) 3α + 3β = 11
Solution:
(c) α + 3β = 11
Hint:
Equation joining (2, 3), (-1, 4)

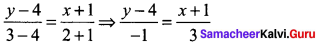
3y – 12 = – x -1 ⇒ x + 3y – 11 = 0, (α, β) lies on it ⇒ α + 3β – 11 = 0.

Question 6.
The slope of the line which makes an angle 45° with the line 3x – y = – 5 are
(a) 1, -1
(b) \(\frac{1}{2},-2\)
(c) \(1, \frac{1}{2}\)
(d) \(2,-\frac{1}{2}\)
Solution:
(c) \(1, \frac{1}{2}\)
Hint:
Equation of line 3x – y = -5, y = 3x + 5, m₁ = 3

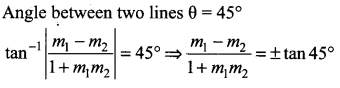
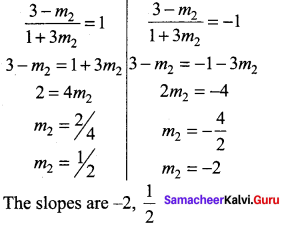
Question 7.
Equation of the straight line that forms an isosceles triangle with coordinate axes in the I-quadrant with perimeter \(4+2 \sqrt{2}\) is
(a)x + y + 2 = 0
(b) x + y – 2 = 0
(c) x + y – \(\sqrt{2}\) = 0
(d) x + y + \(\sqrt{2}\) = 0
Solution:
(b) x + y – 2 = 0
Hint.
Let the sides be x, x

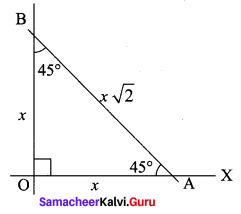
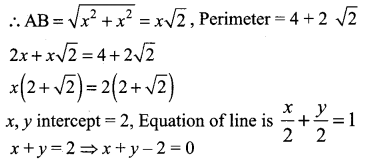
Question 8.
The coordinates of the four vertices of a quadrilateral are (-2, 4), (-1, 2), (1, 2) and (2, 4) taken in order. The equation of the line passing through the vertex (-1, 2) and dividing the quadrilateral into the equal areas is ………
(a) x + 1 = 0
(b) x + y = 1
(c) x + y + 3 = 0
(d) x – y + 3 = 0
Solution:
(b) x + y = 1
Hint:
This equation passes through (-1, 2)
-1 + 2 = 1 ⇒ 1 = 1

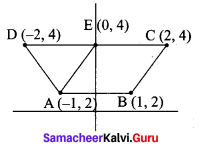
Question 9.
The intercepts of the perpendicular bisector of the line segment joining (1, 2) and (3, 4) with coordinate axes are ……….
(a) 5, -5
(b) 5, 5
(c) 5, 3
(d) 5, -4
Solution:
(b) 5, 5

Question 10.
The equation of the line with slope 2 and the length of the perpendicular from the origin equal to \(\sqrt{5}\) is ……
(a) x + 2y = \(\sqrt{5}\)
(b) 2x + y = \(\sqrt{5}\)
(c) 2x + y = 5
(d) x + 2y – 5 = 0
Solution:
(c) 2x + y = 5

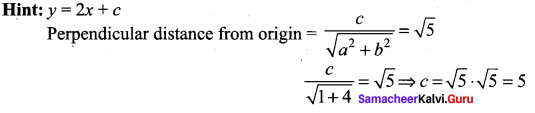
The required line is y = 2x + 5 ⇒ 2x – y + 5 = 0

Question 11.
A line perpendicular to the line 5x – y = 0 forms a triangle with the coordinate axes. If the area of the triangle is 5 sq. units, then its equation is …….

Solution:
(a) x + 5y ± 5\(\sqrt{2}\) = 0
Hint:
Equation of a line perpendicular to 5x – y = 0 is

Question 12.
Equation of the straight line perpendicular to the line x – y + 5 = o, through the point of intersection the y-axis and the given line …….
(a) x – y – 5 = 0
(b) x + y – 5 = 0
(c) x + y + 5 = 0
(d) x + y + 10 = 0
Solution:
(b) x + y – 5 = 0
Hint:
x – y + 5 = 0 ⇒ put x = 0, y = 5
The point is (0, 5)
Equation of a line perpendicular to x – y + 5 = 0 is x + y + k = 0
This passes through (0, 5)
k = -5
x + 7 – 5 = 0

Question 13.
If the equation of the base opposite to the vertex (2, 3) of an equilateral triangle is x + y = 2, then the length of a side is ………

Solution:
\(\sqrt{6}\)
Hint:
In an equilateral, ∆ the perpendicular wall bisects the base into two equal parts. Length of the perpendicular drawn from (2, 3) to the line x + 7 – 2 = 0

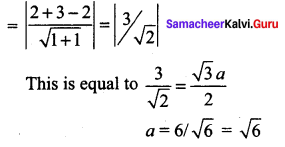
Question 14.
The line (p + 2q) x + (p – 3q)y = p – q for different values of p and q passes through the point ……

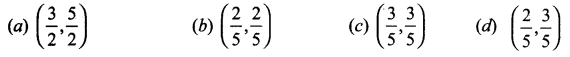
Solution:
(d) \(\left(\frac{2}{5}, \frac{3}{5}\right)\)
Hint:
(p + 2 q)x + (p – 3q)y = p – q
px + 2qx + py – 3qy = p – q
P(x + y) + q (2x – 3y) = p – q
The fourth option x = 2/5, y = 3/5

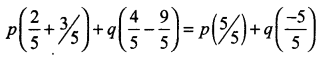
= p – q = RHS

Question 15.
The point on the line 2x – 3y = 5 is equidistance from (1, 2) and (3, 4) is …
(a) (7, 3)
(b) (4, 1)
(c) (1, -1)
(d) (-2, 3)
Solution:
(b) (4, 1)
Hint:
Let (a, b) be on 2x – 3y = 5 ⇒ 2a – 3b = 5
It is equidistance from (1, 2) and (3, 4)

(a – 1)² + (b – 2)² = (a – 3)² + (6 – 4)²
a² – 2a + 1 + b² – 4b + 4 = a² – 6a + 9 + b² – 8b + 16
4a + 4b = 20
2a+ 2b = 10
2a – 3b = 5
5b = 5
b = 1 ∴ a = 4
∴ The point is (4, 1)

Question 16.
The image of the point (2, 3) in the line y = – x is ………
(a) (-3, -2)
(b) (-3, 2)
(c) (-2, -3)
(d) (3, 2)
Solution:
(a) (-3, -2)

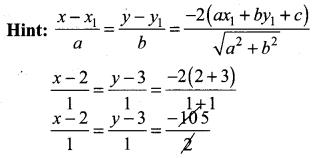
x – 2 = -5, y – 3 = -5
x = -3, y = -2
(-3,-2)

Question 17.
The length of ⊥ from the origin to the line \(\frac{x}{3}-\frac{y}{4}=1\) is ……

Solution:
(c) \(\frac{12}{5}\)
Hint:
4x – 3y = 12 ⇒ 4x – 3y – 12 = 0

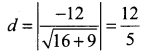
Question 18.
The y-intercept of the straight line passing through (1, 3) and perpendicular to 2x – 3y + 1 = 0 is ……..

Solution:
(b) \(\frac{9}{2}\)
Hint:
Equation of a line perpendicular to 2x – 3y + 1 = 0 is 3x + 2y = k. It passes through (1, 3).
3 + 6 = k ⇒ k = 9, 3x + 2y = 9
To find y-intercept x = 0, 2y = 9, y = 9/2

Question 19.
If the two straight lines x + (2k – 7)y + 3 = 0 and 3kx + 9y – 5 = 0 are perpendicular then the value of k is ……

Solution:
(a) k = 3
Hint.

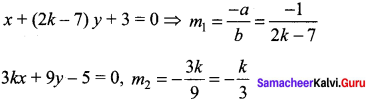
Since the lines are perpendicular m₁m₂ = – 1

Question 20.
If a vertex of a square is at the origin and it’s one side lies along the line 4x + 3y – 20 = 0, then the area of the square is ……..
(a) 20 sq. units
(b) 16 sq. units
(c) 25 sq. units
(d) 4 sq. units
Solution:
(b) 16 sq. units
Hint:
One side of a square = Length of the perpendicular from (0, 0) to the line.

Question 21.
If the lines represented by the equation 6x² + 41xy – 7y² = 0 make angles α and β with the x-axis, then tan α tan β =

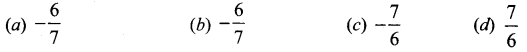
Solution:
(a) \(-\frac{6}{7}\)
Hint.
6x² + 41xy – 7y² = 0
⇒ 6x² – xy + 42xy – 7y² = 0
⇒ x (6x – y) + 7y (6x – y) = 0
⇒ (x + 7y) (6x – y) = 0
⇒ x + 7y = 0, 6x – y = 0

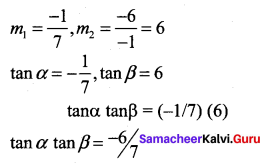
Question 22.
The area of the triangle formed by the lines x² – 4y² = 0 and x = a is …….

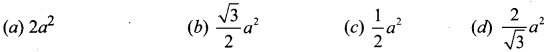
Solution:
(c) \(\frac{1}{2} a^{2}\)
Hint:
x² – 4y² = 0 , (x – 2y) (x + 2y) = 0 ⇒ x – 2y = 0, x + 2y = 0

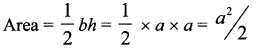
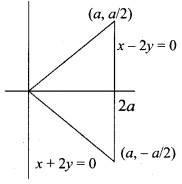
Question 23.
If one of the lines given by 6x² – x + 4x² = 0 is 3x + 4y = 0, then c equals to ……
(a) -3
(b) -1
(c) 3
(d) 1
Solution:
(a) -3
Hint.
6x² – xy + 4cy² = 0, 3x + 4y = 0
The other line may be (2x + by)
(3x + 4y) (2x + by) = 6x² – xy + 4cy²
6x² + 3xby + 8xy + 4by² = 6x² – xy + 4cy²
6x² + xy (3b + 8) + 4by² = 6x² – xy + 4cy²
paring, 3b + 8 = -1
3b = -9 ⇒ b = -3
4b = 4c ⇒ 4(-3) = 4c
-12 = 4c ⇒ c = -3

Question 24.


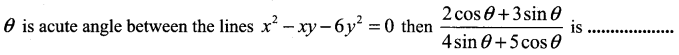
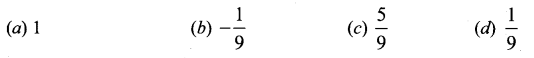
Solution:
(c) \(\frac{5}{9}\)
Hint:

Question 25.
The equation of one the line represented by the equation x² + 2xy cot θ – y² = 0 is ………
(a) x – y cotθ = 0
(b) x + y tan θ = 0
(e) x cos θ + y(sin θ + 1) = 0
(d) x sin θ + y(cos θ + 1) = 0
Solution:
(d) x sin θ + y(cos θ + 1)=0