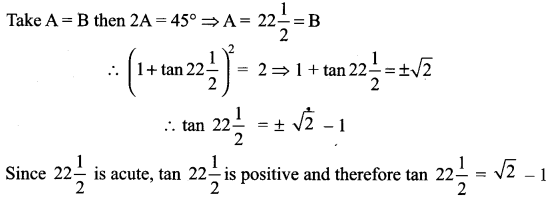Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.4

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.4

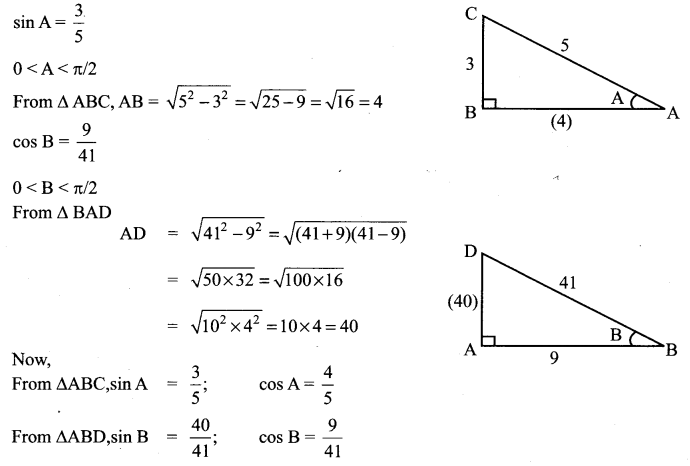
Question 1.

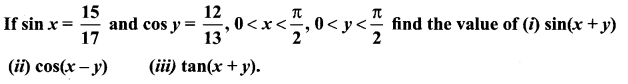
Solution:

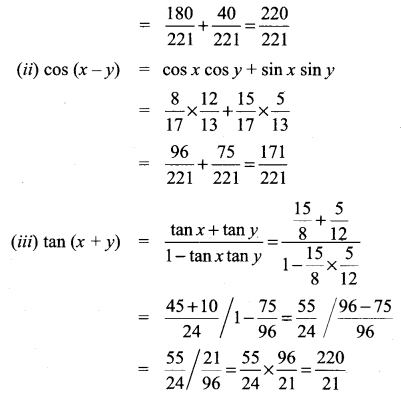
Question 2.

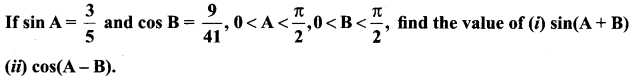
Solution:

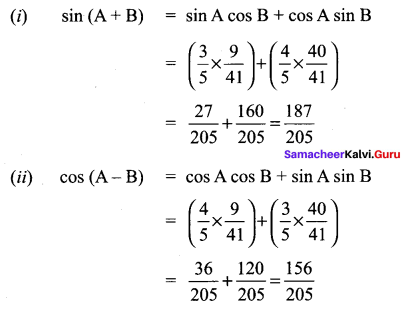
Question 3.

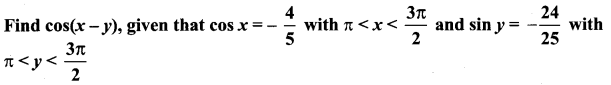
Solution:


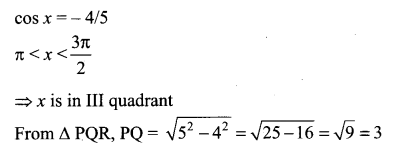
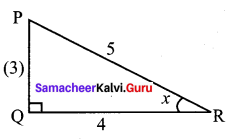
since x is in III quadrant
Both sin x and cos x are negative

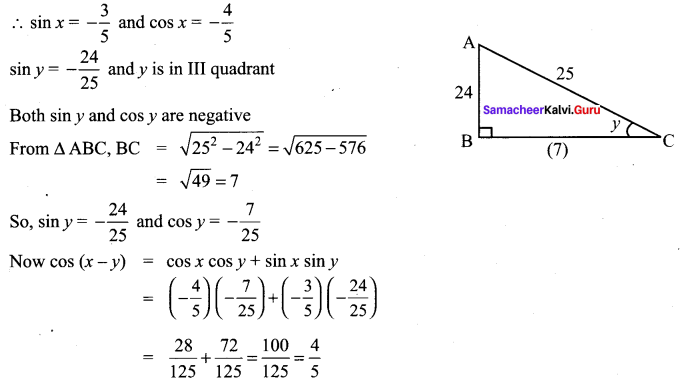
Question 4.

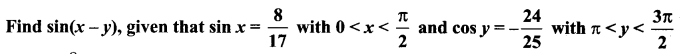
Solution:

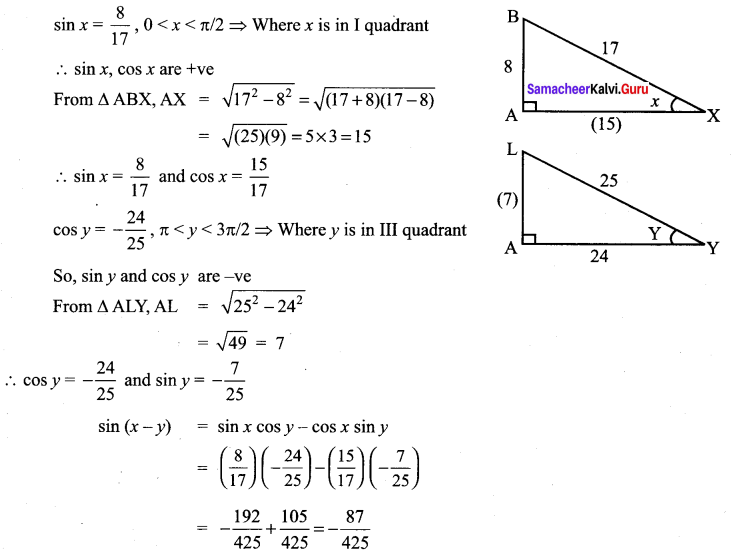
Question 5.

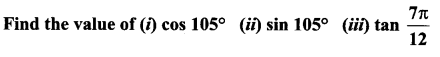
Solution:

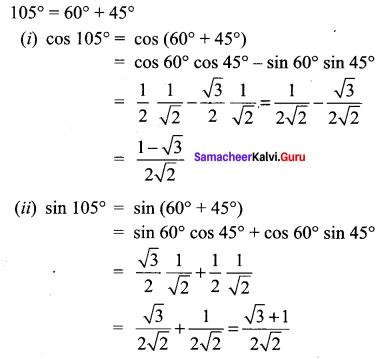
Question 6.

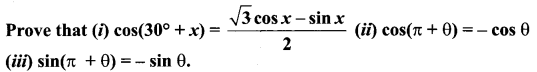
Solution:

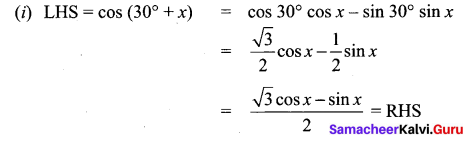
(ii) cos (π + θ) = – cos θ
cos (π + θ) = cos π cos θ – sin π sin θ
= (- 1) cos θ – (0) sin θ
cos (π + θ) = – cos θ

(iii) sin (π + θ) = – sin θ
sin (π + θ) = sin π cos θ + cos π sin θ
= (0) cos θ + (- 1) sin θ
sin (π + θ) = 0 – sin θ = – sin θ

Question 7.
Find a quadratic equation whose roots are sin 15° and cos 15°
Solution:

Question 8.
Expand cos(A + B + C). Hence prove that cos A cos B cos C = sin A sin B cos C + sin B sin C cos A + sin C sin A cos B, if A + B + C = \(\frac{\pi}{2}\)
Solution:
cos(A + B + C) = cos (A + (B + C))
= cos A cos (B + C) – sin A sin (B + C)
= cos A [ cos B cos C – sin B sin C] – sin A [sin B cos C + cos B sin C]
= cos A cos B cos C – cos A sin B sin C – sin A sin B cos C – sin A cos B sin C
Given A + B + C = \(\frac{\pi}{2}\)
∴ cos\(\left(\frac{\pi}{2}\right)\) = cos A cos B cos C – cos A sin B sin C – sin A sin B cos C – sin A cos B sin C
0 = cos A cos B cos C – cos A sin B sin C – sin A sin B cos C – sin A cos B sin C
cos A cos B cos C = cos A sin B sin C + sin A sin B cos C + sin A cos B sin C

Question 9.
Prove that
(i) sin(45° + θ) – sin(45° – θ) = \(\sqrt{2}\)sin θ.
(ii) sin(30° + θ) + cos(60° + θ) = cos θ.
Solution:

Question 10.
If a cos(x + y) = b cos(x – y), show that (a + b) tan x = (a – b) cot y.
Solution:
a cos (x + y) = b cos (x – y)
a[cos x cos y – sin x sin y] = 6[cos x cos y + sin x sin y]
(i.e) a cos x cos y – a sin x sin y = b cos x cos y + b sin x sin y
a cos x cos y – b sin x sin y = a sin x sin y + b cos x cos y

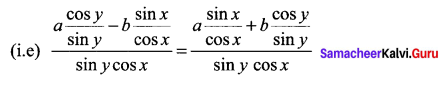
⇒ a cot y – b tan x = a tan x + b cot y
a cot y – b cot y = a tan x + b tan x
⇒ (a + b) tan x = (a – b) cot y.

Question 11.
Prove that sin 105° + cos 105° = cos 45°.
Solution:
sin 105° = sin (60°+ 45°)
= sin 60° cos 45° + cos 60° cos 45°

= cos 45° = RHS

Question 12.
Prove that sin 75° – sin 15° = cos 105° + cos 15°.
Solution:
sin 75° – sin 15° = sin (45° + 30°) – sin (45° – 30°)
= (sin 45° cos 30° + cos 45° sin 30°) – (sin 45° cos 30° – cos 45° sin 30°)
= sin 45° cos30° + cos 45° sin 30° – sin 45° cos 30° + cos 45° sin 30°
= 2 cos 45° sin 30°
sin 75° – sin 15° = 2 × \(\frac{1}{\sqrt{2}}\) × \(\frac{1}{2}\) = \(\frac{1}{\sqrt{2}}\) ——— (1)
cos 105° + cos 15° = cos (90° + 15°) + cos 15°
= – sin 15° + cos 15°
= cos 15° – sin 15°
= cos(45° – 30°) – sin(45° – 30°)
= (cos 45° cos 30°+ sin 45° sin 30°) – (sin 45° cos 30° – cos 45° sin 30°)

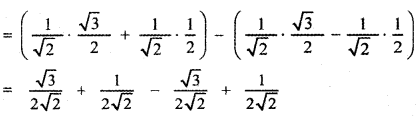
cos 105° + cos 15° = \(\frac{2}{2 \sqrt{2}}\) = \(\frac{1}{\sqrt{2}}\) ——— (2)
From equations (1) and (2)
sin 75° – sin 15° = cos 105° + cos 15°

Question 13.
Show that tan 75° + cot 75° = 4
Solution:

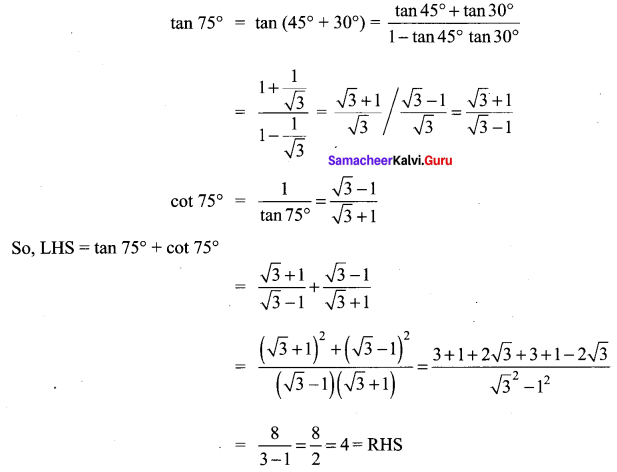
Question 14.
Prove that cos(A + B) cos C – cos(B + C) cos A = sin B sin(C – A).
Solution:
cos (A + B) cos C = (cos A cos B – sin A sin B) cos C
cos (A + B) cos C = cos A cos B cos C – sin A sin B cos C ——— (1)
cos (B + C) cos A = (cos B cos C – sin B sin C) cos A
cos (B + C) cos A = cos A cos B cos C – cos A sin B sin C ——— (2)
Equation (1) – (2) ⇒
Cos (A + B) cos C – cos (B + C) cos A = cos A cos B cos C – sin A sin B cos C – cos A cos B cos C + cos A sin B sin C
= sin A sin B cos C + cos A sin B sin C
= sin B (cos C cos A + sin C sin A)
= sin B cos (C – A)

Question 15.
Prove that sin(n + 1) θ sin(n – 1) θ + cos(n + 1) θ cos(n – 1)θ = cos 2θ, n ∈ Z.
Solution:
cos (n + 1)θ cos(n – 1)θ + sin(n + 1)θ sin(n – 1)θ
= cos [(n + 1)θ – (n – 1)θ]
= cos [nθ + θ – nθ + θ]
= cos 2θ, n ∈ Z

Question 16.

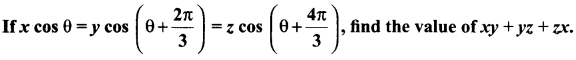
Solution:

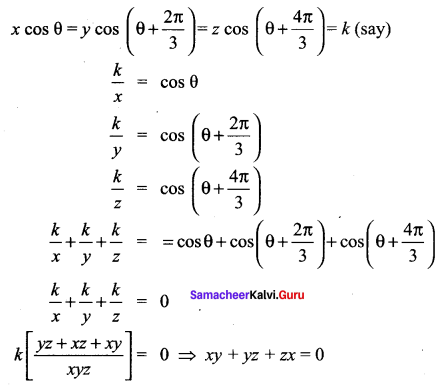
Question 17.
Prove that
(i) sin(A + B) sin(A – B) = sin² A – sin² B
(ii) cos(A + B) cos(A – B) = cos² A – sin² B = cos² B – sin² A
(iii) sin²(A + B) – sin²(A – B) = sin2A sin2B
(iv) cos 8θ cos 2θ = cos² 5θ – sin² 3θ
Solution:
(i) sin(A + B) sin(A – B)= (sin A cos B + cos A sin B) (sin A cos B – cos A sin B)
= sin²A cos²B – cos²A sin²B = sin²A (1 – sin²B) – (1 – sin²A) sin²B
= sin²A – sin²A sin²B – sin²B + sin²A sin² B
= sin²A – sin² B

(ii) LHS = cos (A + B) cos (A – B) = (cos A cos B – sin A sin B) (cos A cos B + sin (A sin B)
= cos² A cos² B – sin² A sin² B
= cos² A (1 – sin² B) – (1 – cos² A) sin² B
= cos² A – cos² A sin² B – sin² B + cos² A sin² B
= cos² A – sin² B = RHS
Now cos² A – sin² B = (1 – sin² A) – (1 – cos² B)
= 1 – sin² A – 1 + cos² B
= cos² B – sin² A

(iii) sin²(A + B) – sin²(A – B) = (sin(A + B) + sin(A – B)) (sin(A + B) – sin(A – B))
= [sin A cos B + cos A sin B + sin A cos B – cos A sin B] × [(sin A cos B + cos A sin B) – (sin A cos B – cos A sin B)]
= (2 sin A cos B) × [sin A cos B + cos A sin B – sin A cos B + cos A sin B]
= (2 sin A cos B) (2 cos A sin B)
= (2 sin A cos A)(2 sin B cos B)
= sin²A . sin²B

(iv) LHS = cos 8θ cos 2θ
= cos (5θ + 3θ) cos (5θ – 3θ) .
We know cos (A + B) cos (A – B) = cos² A – sin² B
∴ cos (5θ + 3θ) cos (5θ – 3θ) = cos² 5θ – sin² 3θ = RHS

Question 18.
Show that cos² A + cos² B – 2 cos A cos B cos(A + B) = sin²(A + B).
Solution:
sin²(A + B) = [sin(A + B)]²
= (sin A cos B + cos A sin B )²
= sin² A cos² B + cos² A sin² B + 2 sin A cos B cos A sin B
= (1 – cos²A) cos²B + cos² A ( 1 – cos²B) + 2 sin A sin B cos A cos B
= cos² B – cos²A cos²B + cos²A – cos²A cos² B + 2 sin A sin B cos A cos B
= cos² A + cos² B – 2cos² A cos² B + 2 sin A sin B cos A cos B
= cos² A + cos² B – 2 cos A cos B (cos A cos B – sin A sin B)
sin² (A + B) = cos² A + cos² B – 2 cos A cos B cos(A + B)

Question 19.
If cos(α – β) + cos(β – γ) + cos(γ – α) = \(-\frac{3}{2}\), then prove that cos α + cos β + cos γ = sin α + sin β + sin γ
Solution:

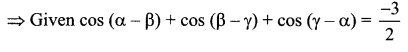
2 cos (α – β) + 2cos (β – γ) + 2cos (γ – α) = -3
2cos(α – β) + 2cos(β – γ) + 2cos (γ – α) + 3 = 0
[2 cos α cos β + 2 sin α sin β] + [2 cos β cos γ + 2 sin β sin γ] + [2 cos γ cos α + sin γ sin α] + 3 = 0
= [2 cos α cos β + 2 cos β cos γ + 2 cos γ cos α] + [2 sin α sin β + 2 sin β sin γ + 2 sin γ sin α] + (sin² α + cos² α) + (sin² β + cos² β) + (sin² γ + cos² γ) = 0
⇒ (cos² α + cos² β + cos² γ + 2 cos α cos β + 2 cos β cos γ + 2 cos γ cos α) + (sin² α + sin² β) + (sin² γ + 2 sin α sin β + 2 sin β sin γ + 2 sin γ sin α) = 0
(cos α + cos β + cos γ)² + (sin α + sin β + sin γ)² = 0
=(cos α + cos β + cos γ) = 0 and sin α + sin β + sin γ = 0
Hence proved

Question 20.

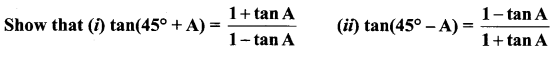
Solution:

Question 21.

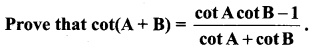
Solution:

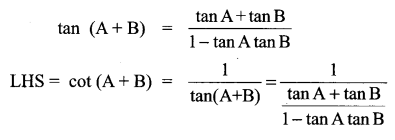
Question 22.

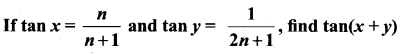
Solution:

Question 23.

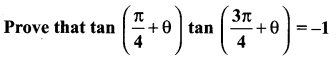
Solution:

Question 24.

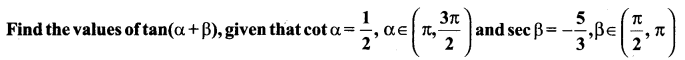
Solution:

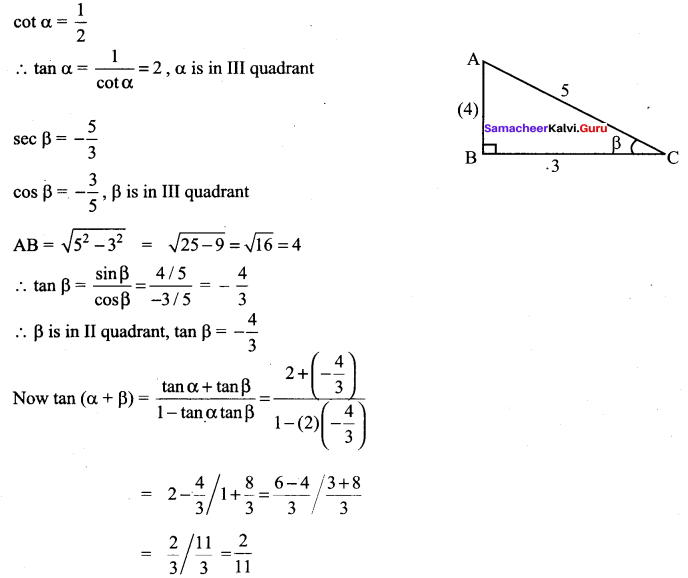
Question 25.

Solution:

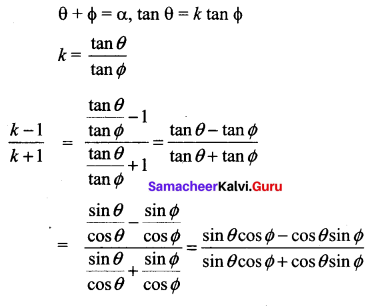
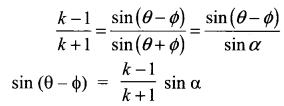
Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.4 Additinal Questions

Question 1.
Prove that sin (A + B) sin (A – B) = cos² B – cos² A
Solution:
LHS = sin (A + B) sin (A – B)
= (sin A cos B + cos A sin B) (sin A cos B – cos A sin B)
= sin² A cos² B – cos² A sin² B
= (1 – cos² A) cos² B – cos² A (1 – cos² B)
= cos² B – cos² A cos² B – cos² A + cos² A cos² B
= cos² B – cos² A = RHS

Question 2.
Prove that
(i) sin A + sin(120° + A) + sin (240° + A) = 0
(ii) cos A + cos (120° +A) + cos (120° – A) = 0
Solution:
(i) sin A + sin(120° + A) + sin (240° + A)
= sin A+ sin 120° cos A + cos 120° sin A + sin 240° cos A + cos 240° sin A …… (1)

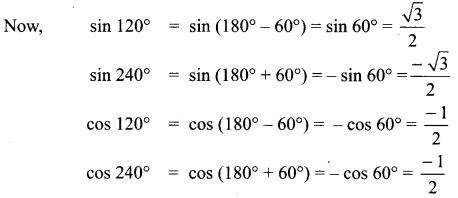
By substituting these values in (1), we get,

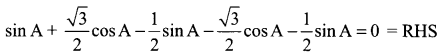
(ii) cos 120° = cos (180° – 60°) = – cos 60° = \(\frac{-1}{2}\)
LHS = cos A + cos (120° + A) + cos (120° – A)
= cos A + cos 120° cos A – sin 120° sin A + cos 120° cos A + sin 120° sin A
= cos A + 2 cos 120° cos A

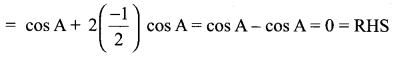
Question 3.

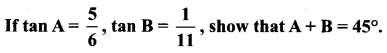
Solution:

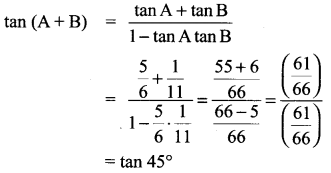
tan (A + B) = 1 ⇒ A+ B = 45°

Question 4.
If A + B = 45°, show that (1 + tan A) (1 + tan B) = 2 and hence deduce the value of tan \(22 \frac{1^{0}}{2}\).
Solution:
Given A + B = 45° ⇒ tan (A + B) = tan 45°

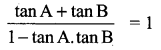
(i.e.) tan A + tan B = 1 – tan A.tan B
(i.e.) 1 + tan A + tan B = 2 – tan A tan B (add 1 on both sides)
1 + tan A + tan B + tan A tan B = 2
(i.e.) (1 + tan A) (1 + tan B) = 2