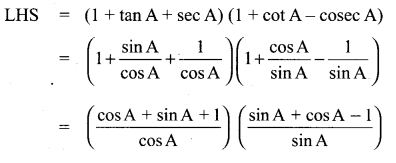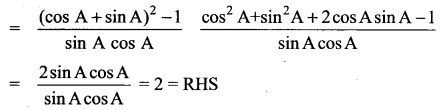You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.1
Question 1.
Identify the quadrant in which an angle of each given measure lies
(i) 25°
(ii) 825°
(iii) -55°
(iv) 328°
Solution:
(i) 25° = I quadrant
(ii) 825° = 105° (90° + 15°) = II quadrant
(iii) -55° = IV quadrant
(iv) 328° = IV quadrant (270° + 58°)
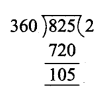
(v) -230° = 360° – 230° = 130° = (90° + 40°) II quadrant
![]()
Question 2.
For each given angle, find a coterminal angle with measure of θ such that θ° < θ < 360°
(i) 395°
(ii) 525°
(iii) 1150°
(iv) -270°
(v) -450°
Solution:
(i) 395° = 360° + 35°
∴ coterminal angle = 35°
(ii) 525° – 360°= 165°
coterminal angle = 165°
(iii) 1150° = 360 × 3 + 70° = 70°
coterminal angle = 70°
(iv) -270° = coterminal angle =+90° {270° + 90° = 360°}
(v) -450° = -360° – 90° = -90°
∴ coterminal angle = 360° – 90° = 270°
Question 3.
![]()
Solution:
a cos θ – b sin θ = c
⇒ (a cos θ – b sin θ)2 = c2
(i.e) a2 cos2 θ + b2 sin2 θ – 2ab sin θ cos θ = c2
(i.e) a2 (1 – sin2 θ) + b2 (1 – cos2 θ) – 2ab sin θ cos θ = c2
a2 – a2 sin2 θ + b2 – b2 cos2 θ – 2ab sin θ cos θ = c2
a2 + b2 – c2 = a2 sin2 θ + b2 cos2 θ + 2ab sin θ cos θ
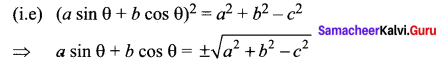
![]()
Question 4.
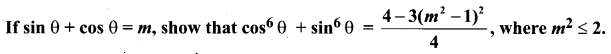
Solution:

Question 5.

Solution:
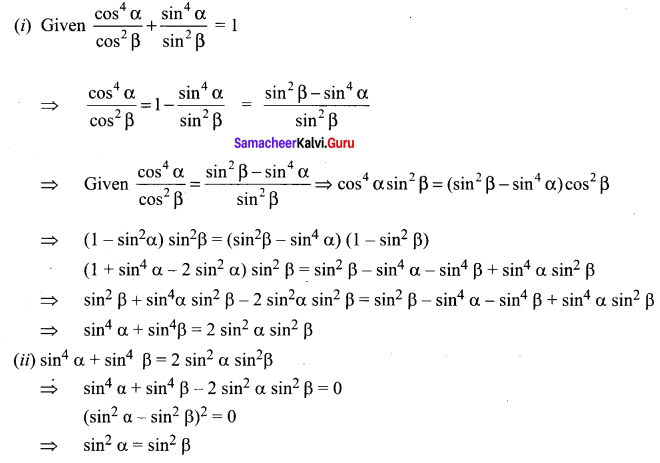
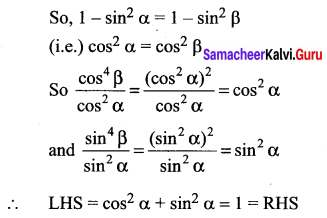
![]()
Question 6.

Solution:
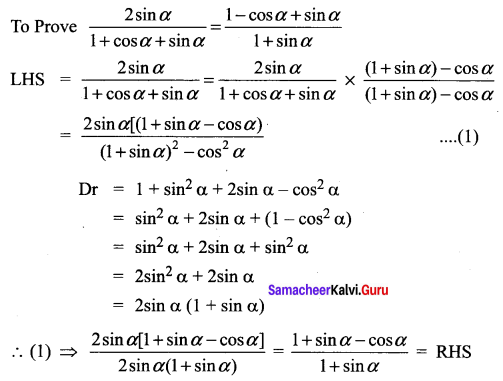
Question 7.
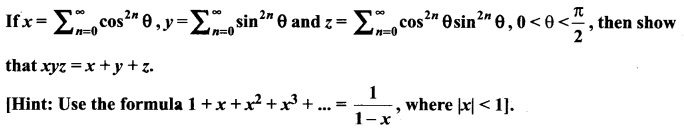
Solution:
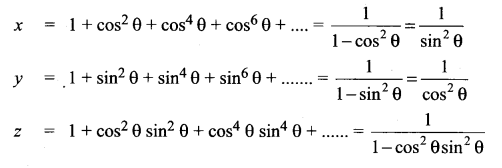

![]()
Question 8.
![]()
Solution:

Question 9.
If sec θ + tan θ = p, obtain the values of sec θ, tan θ and sin θ in terms of p.
Solution:
Given, sec θ + tan θ = p
we know sec2 θ – tan2 θ = 1
(i.e) (sec θ + tan θ) (sec θ – tan θ) = 1

Question 10.
If cot θ (1 + sin θ) = 4m and cot θ (1 – sin θ) = 4n, then prove that (m2 – n2)2 = mn.
Solution:
cot θ (1 + sin θ) = 4m


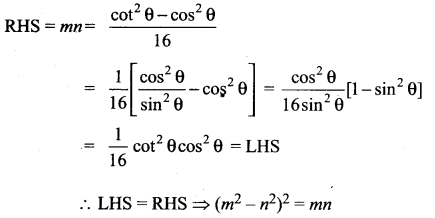
Question 11.
If cosec θ – sin θ = a3 and sec θ – cos θ = b3, then prove that a2b2 (a2 + b2) = 1.
Solution:

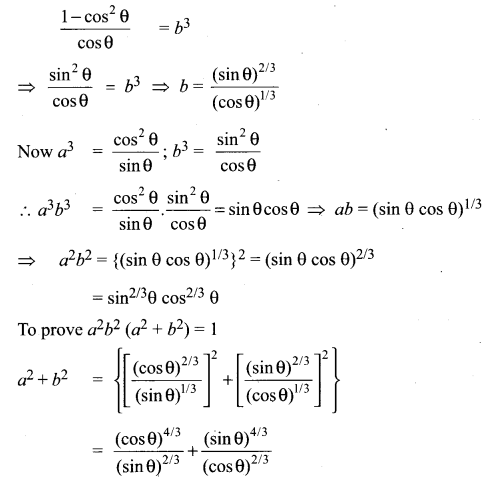
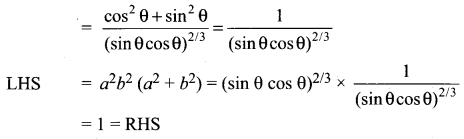
![]()
Question 12.
Eliminate θ from the equations a sec θ – c tan θ = b and b sec θ + d tan θ = c.
Solution:
Taking sec θ = X and tan θ = Y we get the equations as


Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.1 Additional Equations
Question 1.
Prove that (sec θ + cos θ) (sec θ – cos θ) = tan2 θ + sin2 θ
Solution:
(sec θ + cos θ) (sec θ – cos θ) = sec2 θ – cos2 θ
= (1 + tan2 θ ) – (1 – sin2 θ)
= tan2 θ + sin2 θ = RHS
Question 2.
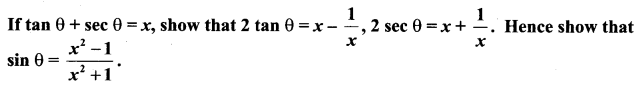
Solution:

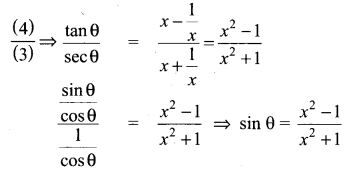
Question 3.
![]()
Solution:

![]()
Question 4.
![]()
Solution:
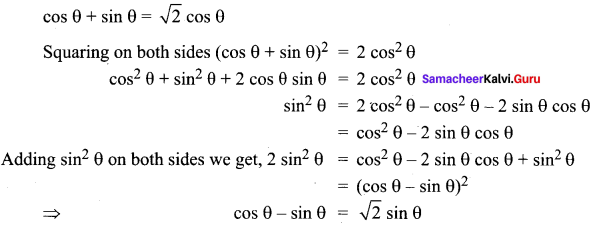
Question 5.
Prove that (1 + tan A + sec A) (1 + cot A – cosec A) = 2
Solution:
LHS = (1 + tan A + sec A) (1 + cot A – cosec A)