You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 1 Sets Ex 1.2
Question 1.
Discuss the following relations for reflexivity, symmetricity and transitivity:
(i) The relation R defined on the set of all positive integers by “mRn if m divides n”.
Solution:
Let Z = {1, 2, 3, ……….}
R is a relation defined on the set of all positive integers by m R n if m divides n
R = { (m, n) : \(\frac{\mathrm{m}}{\mathrm{n}}\) for all m, n ∈ Z } n
(a) Reflexive:
m divides m for all m ∈ Z
∴ (m, m) ∈ R for all m ∈ Z
Hence R is reflexive
(b) Symmetric:
Let (m, n) ∈ R ⇒ m divides n
⇒ n = km for some integers k
But km need not divide m, ie. n need not divide m
∴ (n, m) ∉ R
Hence R is not symmetric.
(c) Transitive:
Let (m, n), (n, r) ∈ R
Then m divides n ⇒ n = km and
n divides r ⇒ r = k1n
r = k1(km) = (k1k) m
m divides r
∴ (m, r) ∈ R
Hence R is transitive.
(ii) Let P denote the set of all straight lines in a plane. The relation R defined by “lRm if l is perpendicular to m”.
Solution:
P = {set of all straight lines in a plane}
lRm ⇒ l is perpendicular to m
(a) lRl ⇒ l is not perpendicular to l
⇒ It is not reflexive
(b) lRm ⇒ l is perpendicular to m
mRl ⇒ m is perpendicular to l
It is symmetric
(c) l perpendicular to m ⇒ m perpendicular to n ⇒ l is parallel to n It is not transitive
![]()
(iii) Let A be the set consisting of all the members of a family. The relation R defined by “aRb if a is not a sister of b”.
Solution:
Let F = Father,
M = Mother
G = Male child
H = Female child
A = { F, M, G, H }
The relation R is defined by
a R b if a is not a sister of b.
R = {(F, F), (F, M), (F, G), (F, H), (M, F), (M, M), (M, G), (M, H), (G, F), (G, M), (G, G), (G, H), (H, F), (H, M), (H, H)}
(a) Reflexive:
(F, F) , (M , M), (G, G), ( H, H ) ∈ R
∴ R is reflexive.
(b) Symmetric:
For (G, H) ∈ R, we have (H, G) ∉ R
∴ R is not symmetric.
(c) Transitive:
Suppose in a family if we take mother M , male child-G and female child-H.
H is not a sister of M ⇒ HRM, (H, M) ∈ R
M is not a sister of G ⇒ MRG, (M, G) ∈ R
But H is a sister of G ⇒ HRG, (H, G) ∉ R
Thus, for (H, M), (M, G) ∈ R
we have (H, G) ∉ R
∴ R is transitive.
(iv) Let A be the set consisting of all the female members of a family. The relation R
defined by “aRb if a is not a sister of b”.
Solution:
A = {set of all female members of a family}
(a) aRa ⇒ a is a sister of a
It is reflexive
(b) aRb ⇒ a is a sister of b
bRa ⇒ b is the sister of a
⇒ It is symmetric
(c) aRb ⇒ a is a sister of b bRc ⇒ b is a sister of c aRc ⇒ a can be the sister of c It is not transitive.
(v) On the set of natural numbers the relation R defined by “xRy if x + 2y = 1”.
Solution:
x + 2y = 1 for x, y ∈ N
There is no x , y ∈ N satisfying x + 2y = 1
∴ The relation R is an empty relation.
An empty relation is symmetric and transitive.
∴ R is symmetric and transitive.
R is not reflexive
![]()
Question 2.
Let X = {a, b, c, d} and R = {(a, a), {b, b), (a, c)}. Write down the minimum number
of ordered pairs to be included to R to make it
(i) reflexive
(ii) symmetric
(iii) transitive
(iv) equivalence
Solution:
X = {a, b, c, d}
R = {(a, a), (b, b), (a, c)}
(i) To make R reflexive we need to include (c, c) and (d, d)
(ii) To make R symmetric we need to include (c, a)
(iii) R is transitive
(iv) To make R reflexive we need to include (c, c)
To make R symmetric we need to include (c, c) and (c, a) for transitive
∴ The relation now becomes
R = {(a, a), (b, b), (a, c), (c, c), (c, a)}
∴ R is equivalence relation.
Question 3.
Let A = {a, b, c} and R = {(a, a), (b, b), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it
(i) reflexive
(ii) symmetric
(iii) transitive
(iv) equivalence
Solution:
Given A = {a, b, c }
R = { (a, a), (b, b),(a, c) }
(i) The minimum ordered pair to be included to R in order to make it reflexive is (c, c).
(ii) The minimum ordered pair to be included to R in order to make it symmetrical is (c, a).
(iii) R is transitive. We need not add any pair.
(iv) After including the ordered pairs (c, c),(c, a) to R the new relation becomes
R1 = { (a, a), (b, b), (c, c) , (a, c) , (c, a) }
R1 is reflexive symmetric and transitive.
∴ R1 is an equivalence relation.
![]()
Question 4.
Let P be the set of all triangles in a plane and R be the relation defined on P as aRb if a is
similar to b. Prove that R is an equivalence relation.
Solution:
P = {set of all triangles in a plane}
aRb ⇒ a similar to b
(a) aRa ⇒ every triangle is similar to itself
∴ aRa is reflexive
(b) aRb ⇒ if a is similar to b ⇒ b is also similar to a.
⇒ It is symmetric
(c) aRb ⇒ bRc ⇒ aRc
a is similar to b and b is similar to c
⇒ a is similar to a
⇒ It is transitive
∴ R is an equivalence relation
![]()
Question 5.
On the set of natural numbers let R be the relation defined by aRb if 2a + 3b = 30. Write down the relation by listing all the pairs. Check whether it is
(i) reflexive
(ii) symmetric
(iii) transitive
(iv) equivalence
Solution:
N = {set of natural numbers}
R ={(3, 8), (6, 6), (9, 4), (12, 2)}
(a) (3, 3) ∉ R ⇒ R is not reflexive
2a + 3b = 30
3b = 30 – 2a
b = \(\frac{30-2 a}{3}\)
(b) (3, 8) ∈ R(8, 3) ∉ R
⇒ R is not symmetric
(c) (a, b) (b, c) ∉ R ⇒ R is transitive
∴ It is not an equivalence relation.
Question 6.
Prove that the relation “friendship” is not an equivalence relation on the set of all people in Chennai.
Solution:
If a is a friend of b and b is a friend of c, then a need not be a friend of c.
a R b and b R c does not imply a R c.
∴ R is not transitive.
∴ The relation is not an equivalence relation.
![]()
Question 7.
On the set of natural numbers let R be the relation defined by aRb if a + b ≤ 6. Write down the relation by listing all the pairs. Check whether it is
(i) reflexive
(ii) symmetric
(iii) transitive
(iv) equivalence
Solution:
Set of all natural numbers aRb if a + b ≤ 6
R= {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (2, 1), (2, 2), (2, 3), (2, 4), (3, 1), (3, 2), (3, 3), (4, 1), (4, 2), (5, 1)}
(i) (5, 1) ∈ R but(5, 5) ∉ R
It is not reflexive
(ii) aRb ⇒ bRa ⇒ It is symmetric
(iii) (4, 2), (2, 3) ∈ R ⇒ (4, 3) ∉ R
∴ It is not transitive
(iv) ∴ It is not an equivalence relation
Question 8.
Let A = {a, b, c}. What is the equivalence relation of smallest cardinality on A? What is the equivalence relation of largest cardinality on A?
Solution:
A = { a, b, c }
Let R1 = { (a, a),(b, b),(c, c) }
Clearly, R1 is reflexive, symmetric, and transitive.
Thus R1 is the equivalence relation on A of smallest cardinality, n (R1) = 3
Let R2 = { (a, a), (b, b), (c, c), (a, b), (b, a), (b, c), (c, b), (c, a), (a, c)}
(i) Reflexive:
(a, a) , (b, b) , (c, c) ∈ R
∴ R2 is reflexive.
(ii) Symmetric:
(a , b) ∈ R2 we have (b, a) ∈ R2
(b , c) ∈ R2 we have (c, b) ∈ R2
(c , a) ∈ R2 we have (a, c) ∈ R2
∴ R2 is symmetric.
(iii) Transitive:
(a, b), (b, c) ∈ R2 ⇒ (a, c) ∈ R2
(b, c), (c, a) ∈ R2 ⇒ (b, a) ∈ R2
(c, a) , (a, b) ∈ R2 ⇒ (c, b) ∈ R2
∴ R2 is transitive and R2 is an equivalence relation of largest cardinality.
n (R2) = 9
![]()
Question 9.
In the set Z of integers, define mRn if m – n is divisible by 7. Prove that R is an equivalence relation.
Solution:
mRn if m – n is divisible by 7
(a) mRm = m – m = 0
0 is divisible by 7
∴ It is reflexive
(b) mRn = {m – n) is divisible by 7
nRm = (n – m) = – {m – n) is also divisible by 7
It is symmetric
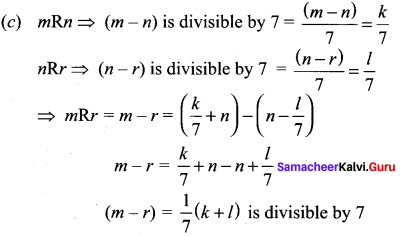
It is transitive
mRn if m – n is divisible by 7
∴ R is an equivalence relation.
Samacheer Kalvi 11th Maths Solutions Chapter 1 Sets Ex 1.2 Additional Questions
Question 1.
Find the range of the function.
f = {(1, x), (1, y), (2, x), (2, y), (3, z)}
Solution:
The range of the function is {x, y, z}.
Question 2.
For n, m ∈ N, It means that it is a factor of n & m. Then find whether the given relation is an equivalence relation.
Solution:
Since n is a factor of n. So the relation is reflexive.
When n is a factor of m (where m ≠ n) then m cannot be a factor of n.
So the relation is not symmetric when n is a factor of m and m is a factor of p then n will be a factor of p. So the given relation is transitive. So it is not an equivalence relation.
![]()
Question 3.
Verify whether the relation “is greater than” is an equivalence relation.
Solution:
You can do it yourself.