You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 7 Mensuration Ex 7.3
Question 1.
A vessel is in the form of a hemispherical bowl mounted by a hollow cylinder. The diameter is 14 cm and the height of the vessel is 13 cm. Find the capacity of the vessel.
Solution:
Diameter = 14 cm
Radius = 7 cm
Total height = 13 cm
Height of the cylindrical part = 13 – 7
= 6 cm
∴ Capacity of the vessel = Capacity of the cylinder + Capacity of the hemisphere.
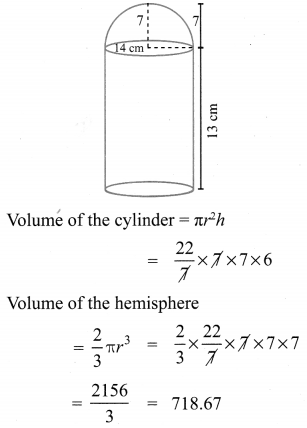
∴ The total volume = 924 + 718.67
The capacity of the vessel = 1642.67 cm3
![]()
Question 2.
Nathan, an engineering student was asked to make a model shaped like a cylinder with two cones attached at its two ends. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of the model that Nathan made.
Solution:
Volume of the model = Volume of the cylinder + Volume of 2 cones.
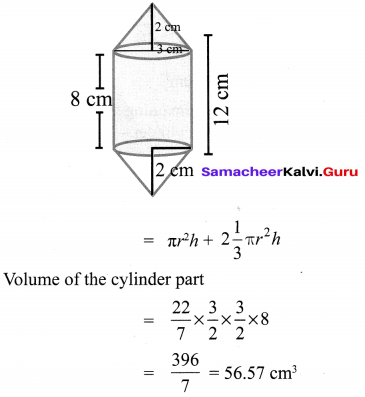

The volume of the model that Nathan made = 66 cm3
Question 3.
From a solid cylinder whose height is 2.4 cm and the diameter 1.4 cm, a cone of the same height and same diameter is carved out. Find the volume of the remaining solid to the nearest cm3.
Solution:
Volume of the cylinder = πr2h cu. units
Volume of the cone = \(\frac{1}{3} \pi r^{2} h\) cu. units
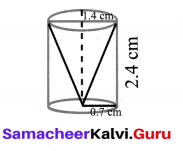
d = 1.4 cm, r = 0.7 cm = \(\frac{7}{10}\)
h = 2.4 cm = \(\frac{24}{10}\)
Volume of the cylinder:
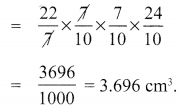
Volume of cone carved out
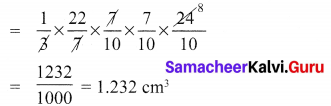
∴ Volume of the remaining solid = Volume of the cylinder – Volume of the cone
= 3.696 – 1.232
= 2.464
= 2.46 cm3
![]()
Question 4.
A solid consisting of a right circular cone of height 12 cm and radius 6 cm standing on a hemisphere of radius 6 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of the water displaced out of the cylinder, if the radius of the cylinder is 6 cm and height is 18 cm.
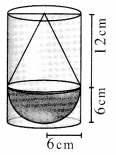
Solution:
Volume of water displaced out = Volume of the solid immersed in.
Volume of the solid = Volume of the cone + Volume of the hemisphere

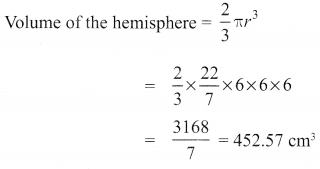
∴ The volume of water displaced out = Volume of the solid
= (1) + (2)
= 905.14 cm3
Question 5.
A capsule is in the shape of a cylinder with two hemisphere stuck to each of its ends. If the length of the entire capsule is 12 mm and the diameter of the capsule is 3 mm, how much medicine it can hold?
Solution:
Volume of medicine the capsule can hold = Volume of the cylinder + 2 volume of hemisphere
Volume of the cylinder part

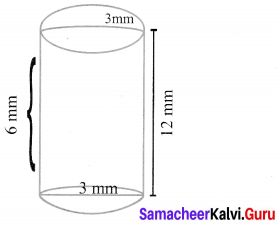
∴ The total volume = 56.571 mm3
∴ The volume of the medicine the capsule can hold = 56.57 mm3
![]()
Question 6.
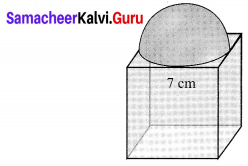
As shown in figure a cubical block of side 7 cm is surmounted by a hemisphere. Find the surface area of the solid.
Solution:
Clearly, greatest diameter of the hemisphere is equal to the length of an edge of the cube is 7 cm.
Radius of the hemisphere = \(\frac{7}{2}\) cm
Now, total surface area of the solid = Surface area of the cube + Curved surface area of the hemisphere – Area of the base of the hemisphere.

Question 7.
A right circular cylinder just enclose a sphere of radius r units.
Calculate
(i) the surface area of the sphere
(ii) the curved surface area of the cylinder
(iii) the ratio of the areas obtained in (i) and (ii).
Solution:
(i) Surface area of sphere = 4πr2 sq. units

Question 8.
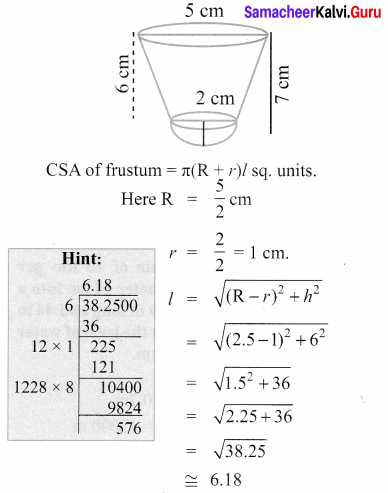
A shuttle cock used for playing badminton has the shape of a frustum of a cone is mounted on a hemisphere. The diameters of the frustum are 5 cm and 2 cm. The height of the entire shuttle cock is 7 cm. Find its external surface area.
Solution:
External surface area of the cock = Surface area of frustum + CSA of hemisphere