Samacheer Kalvi 10th Maths Solutions Chapter 7 Mensuration Ex 7.2

You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 7 Mensuration Ex 7.2

Question 1.
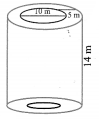
A 14 m deep well with inner diameter 10 m is dug and the earth taken out is evenly spread all around the well to form an embankment of width 5 m. Find the height of the embankment.
Solution:
Inner diameter = 10 m
Inner radius = 5 m
Inner height = 14 m

Volume of the cylinder = πr²h cubic units
\(=\frac{22}{7} \times 5 \times 5 \times 14\)
= 1100 m³
Volume of the hollow = n(R² – r²)h cubic units
R = 10 m
r = 5 m
\(\Rightarrow \frac{22}{7} \times\left(10^{2}-5^{2}\right) h=1100 \mathrm{m}^{3}\)
(∵ the earth taken out = the earth spread all around)

Question 2.
A cylindrical glass with diameter 20 cm has water to a height of 9 cm. A small cylindrical metal of radius 5 cm and height 4 cm is immersed it completely. Calculate the raise of the water in the glass?
Solution:
The volume of the water raised = Volume of the cylindrical metal.

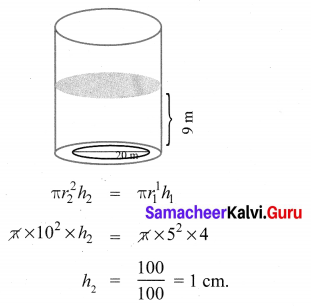
∴ The height of the raised water in the glass = 1 cm.

Question 3.
If the circumference of a conical wooden piece is 484 cm then find its volume when its height is 105 cm.
Solution:
Circumference of the base of the cone = 484 cm
height = 105 cm
∴ 2πr = 484

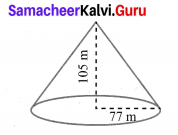
\(r=484 \times \frac{1}{2} \times \frac{7}{22}\)
= 77 cm

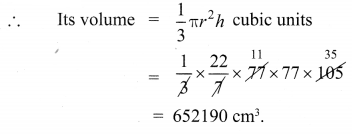
Question 4.
A conical container is fully filled with petrol. The radius is 10m and the height is 15 m. If the container can release the petrol through its bottom at the rate of 25 cu. meter per minute, in how many minutes the container will be emptied. Round off your answer to the nearest minute.
Solution:
Volume of the cone = \(\frac{1}{3} \pi r^{2} h\) cu. units.

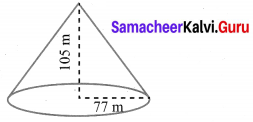
Volume of the given conical container = \(\frac{1}{3} \times \pi \times 10 \times 10 \times 15\)
= 500π m³

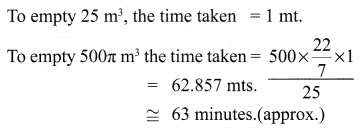
Question 5.
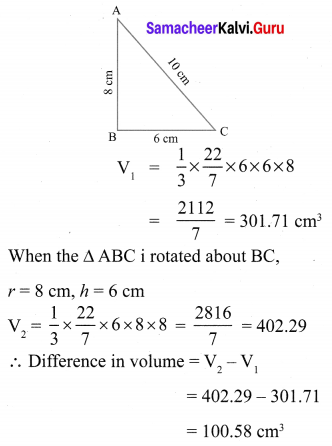
A right angled triangle whose sides are 6 cm, 8 cm and 10 cm is revolved about the sides containing the right angle in two ways. Find the difference in volumes of the two solids so formed.
Solution:
When the triangle ABC is rotated about AB, the

Question 6.
The volumes of two cones of same base radius are 3600 cm³ and 5040 cm³. Find the ratio of heights.
Solution:

Question 7.
If the ratio of radii of two spheres is 4 : 7, find the ratio of their volumes.
Solution:

Question 8.
A solid sphere and a solid hemisphere have equal total surface area. Prove that the ratio of their volume is \(3 \sqrt{3} : 4\)
Solution:

Question 9.
The outer and the inner surface areas of a spherical copper shell are 576π cm² and 324π cm² respectively. Find the volume of the material required to make the shell.
Solution:

Question 10.
A container open at the top is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends are 8 cm and 20 cm respectively. Find the cost of milk which can completely fill a container at the rate of ₹ 40 per litre.
Solution:
Volume of the frustum