You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Unit Exercise 2
Question 1.
Prove that n2 – n divisible by 2 for every positive integer n.
Answer:
To prove n2 – n divisible by 2 for every positive integer n.
We know that any positive integer is of the form 2q or 2q + 1, for some integer q.
So, following cases arise:
Case I. When n = 2q.
In this case, we have
n2 – n = (2q)2 – 2q = 4q2 – 2q = 2q(2q – 1)
⇒ n2 – n = 2r where r = q(2q – 1)
⇒ n2 – n is divisible by 2.
Case II. When n = 2q + 1.
In this case, we have
n2 – n = (2q + 1)2 – (2q + 1)
= (2q + 1)(2q + 1 – 1) = (2q + 1)2q
⇒ n2 – n = 2r where r = q (2q + 1)
⇒ n2 – n is divisible by 2.
Hence n2 – n is divisible by 2 for every positive integer n.
Question 2.
A milk man has 175 litres of cow’s milk and 105 litres of buffalow’s milk. He wishes to sell the milk by filling the two types of milk in cans of equal capacity. Calculate the following (i) Capacity of a can
(ii) Number of cans of cow’s milk
(iii) Number of cans of buffalow’s milk.
Answer:
Cow’s milk = 175 litres
Buffalow’s milk = 105 litres
Find the H.C.F. of 175 and 105 using Euclid’s division method of factorisation method.
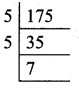
175 = 5 × 5 × 7
105 = 3 × 5 × 7
H.C.F. of 175 and 105 = 5 × 7 = 35
(i) The capacity of the milk can’s is 35 litres
(ii) Cows milk = 175 litres
Number of cans = \(\frac { 175 }{ 35 } \) = 5
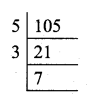
(iii) Buffalow’s milk = 105 litres
Number of cans = \(\frac { 105 }{ 35 } \) = 3
(i) Capacity of one can = 35 litres
(ii) Number of can’s for cow’s milk= 5 litres
(iii) Number of can’s for Buffalow’s milk = 3 litres
Question 3.
When the positive integers a, b and c are divided by 13 the respective remainders are 9, 7 and 10. Find the remainder when a + 2b + 3c is divided by 13.
Answer:
Let the positive integers be a, b, and c.
a = 13q + 9
b = 13q + 7
c = 13q + 10
a + 2b + 3c = 13 q + 9 + 2(13q + 7) + 3(13q + 10)
= 13q + 9 + 269 + 14 + 39q + 30
= 78q + 53 = (13 × 6)q + 53
The remainder is 53.
But 53 = 13 × 4 + 1
∴ The remainder is 1
![]()
Question 4.
Show that 107 is of the form 4q + 3 for any integer q.
Answer:
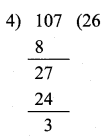
107 = 4 x 26 + 3
This is in the form of a = bq + r
Hence it is proved.
Question 5.
If (m + 1)th term of an A.P. is twice the (n + 1)th term, then prove that (3m + 1)th term is twice the (m + n + 1)th term.
Solution:
tn = a + (n – 1)d
tm+1 = a + (m + 1 – 1)d
= a + md
tn+1 = a + (n + 1 – 1)d
= a + nd
2(tn+1) = 2(a + nd)
tm+1 = 2tn+1 …………… (1)
⇒ a + md = 2(a + nd)
2a + 2nd – a – md = 0
a + (2n – m)d = 0
t(3m+1) = a + (3m + 1 – 1)d
= a + 3md
t(m+n+1) = a + (m + n + 1 – 1)d
= a + (m + n)d
2(t(m+n+1)) = 2(a + (m + n)d)
= 2a + 2md + 2nd
t(3m+1) = 2t(m+n+1) ………….. (2)
a + 3md = 2a + 2md + 2nd
2a + 2md + 2nd – a – 3md = 0
a – md + 2nd = 0
a + (2n – m)d = 0
∴ It is proved that t(3m+1) = 2t(m+n+1)
Question 6.
Find the 12th term from the last term of the A.P -2, -4, -6, … -100.
Solution:
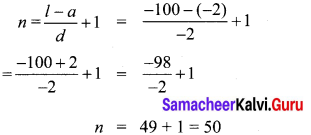
12th term from the last = 39th term from the beginning
∴ t39 = a + 38d
= -2 + 38(-2)
= – 2 – 76
= – 78
Question 7.
Two A.P.’s have the same common difference. The first term of one A.P. is 2 and that of the other is 7. Show that the difference between their 10th terms is the same as the difference between their 21st terms, which is the same as the difference between any two corresponding terms.
Answer:
Let the common difference for the 2 A.P be “d”
For the first A.P
a = 2, d = d, n = 10
tn = a + (n – 1) d
t10 = 2 + 9 d ….(1)
For the 2nd A.P
a = 7, d = d n = 10
t10 = 7 + (9)d
= 7 + 9d ….(2)
Difference between their 10th term ⇒ (1) – (2)
= 2 + 9d – (7 + 9d)
= 2 + 9d – 7 – 9d
= -5
For first A.P when n = 21, a = 2, d = d
t21 = 2 + 20d …….(3)
For second A.P when n = 21, a = 7, d = d
t21 = 7 + 20d …….(4)
Difference between the 21st term ⇒ (3) – (4)
= 2 + 20d – (7 + 20d)
= 2 + 20d – 7 – 20d
= -5
Difference between their 10th term and 21st term = -5
Hence it is proved.
![]()
Question 8.
A man saved ₹16500 in ten years. In each year after the first he saved ₹100 more than he did in the preceding year. How much did he save in the first year?
Solution:
S10 = ₹16500
a, a + d, a + 2d…
d = 100
n = 10
Sn = \(\frac { n }{ 2 } \)(2a+(n-1)d)
S10 = 16500
S10 = \(\frac { 10 }{ 2 } \)(2×a+9×100)
16500 = 5(2a+900)
16500 = 10a + 4500
10a = 16500 – 4500
10a = 12000
a = \(\frac { 12000 }{ 10 } \) = ₹1200
∴ He saved ₹1200 in the first year
Question 9.
Find the G.P. in which the 2nd term is \(\sqrt { 6 }\) and the 6th term is 9\(\sqrt { 6 }\).
Solution:
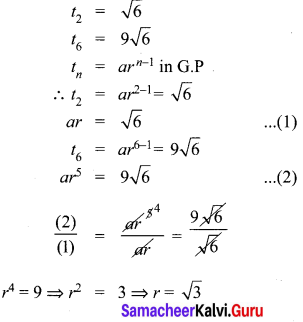
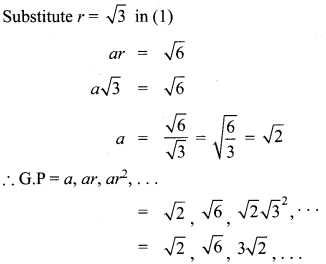
Question 10.
The value of a motorcycle depreciates at the rate of 15% per year. What will be the value of the motor cycle 3 year hence, which is now purchased for ₹45,000?
Answer:
Value of the motor cycyle = ₹ 45000
a = 45000
Depreciation = 15% of the cost value
= \(\frac { 15 }{ 100 } \) × 45000
= 15 × 450
= 6750
d = – 6750 (decrease it is depreciation
Value of the motor cycle lightning of the 2nd year = 45000 – 6750
= ₹ 38250
Depreciation for the 2nd year = \(\frac { 15 }{ 100 } \) × 38250
= ₹ 57370.50