You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.1
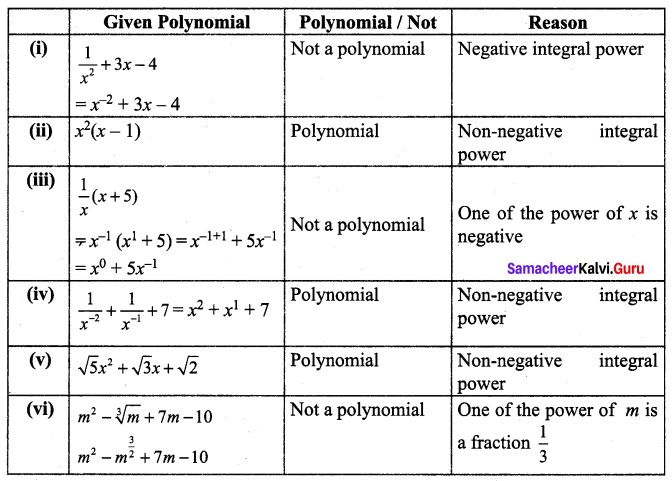
Question 1.
Which of the following expressions are polynomials. If not give reason:
(i) \(\frac{1}{x^{2}}\) + 3x – 4
(ii) x2 (x – 1)
(iii) \(\frac{1}{x}\) (x + 5)
(iv) \(\frac{1}{x^{-2}}+\frac{1}{x^{-1}}\) + 7
(v) \(\sqrt{5} x^{2}+\sqrt{3} x+\sqrt{2}\)
(vi) \(m^{2}-\sqrt[3]{m}+7 m-10\)
Solution:
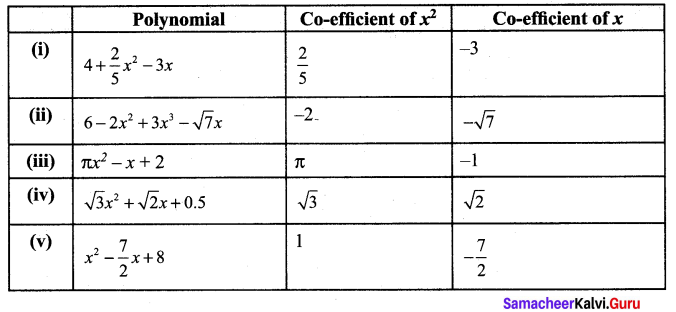
Question 2.
Write the coefficient of x2 and x in each of the following polynomials,
(i) 4 + \(\frac{2}{5} x^{2}\) – 3x
(ii) 6 – 2x2 + 3x3 – \(\sqrt{7} x\)
(iii) πx2 – x + 2
(iv) \(\sqrt{3} x^{2}+\sqrt{2} x\) + 0.5
(v) x2 – \(\frac{7}{2} x\) + 8
Solution:
Question 3.
Find the degree of the following polynomials.
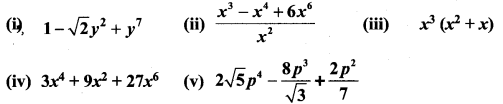
Solution:

![]()
Question 4.
Rewrite the following polynomial in standard form.
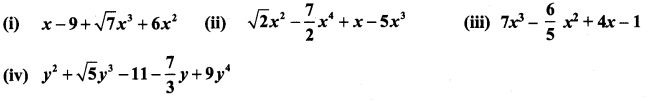
Solution:

Question 5.
Add the following polynomials and find the degree of the resultant polynomial.
(i) p(x) = 6x2 – 7x+ 2 q(x) = 6x3 – 7x + 15
(ii) h(x) = 7x3 – 6x + 1 f(x) = 7x2 + 17x – 9
(iii) f(x) = 16x4 – 5x2 + 9 g(x) = -6x3 + 7x – 15
Solution:

Question 6.
Subtract the second polynomial from the first polynomial and find the degree of the resultant polynomial.
(i) p(x) = 7x2 + 6x – 1 q(x) = 6x – 9
(ii) f(y) = 6y2 – 7y + 2 g(y) = 7y + y3
(iii) h(z) = z5 – 6z4 + z f(z) = 6z2 + 10z – 7
Solution:

Question 7.
What should be added to 2x3 + 6x2 – 5x + 8 to get 3x3 – 2x2 + 6x + 15?
Solution:
(2x3 + 6x2 – 5x + 8) + Q(x) = 3x3 – 2x2 + 6x + 15
∴ Q(x) = (3x3 – 2x2 + 6x + 15) – (2x3 + 6x2 – 5x + 8)
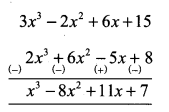
The required polynomial is x3 – 8x2 + 11x + 7
Question 8.
What must be subtracted from 2x24 + 4x2 – 3x + 7 to get 3x3 – x2 + 2x + 1 ?
Solution:
(2x4 + 4x2 – 3x + 7) – Q(x) = 3x3 – x2 + 2x + 1
Q(x) = (2x4 + 4x2 – 3x + 7) – 3x3 – x2 + 2x + 1
The required polynomial = 2x4 + 4x2 – 3x + 7 – 3x3 + x2 – 2x – 1
= 2x4 – 3x3 + 5x2 – 5x + 6
![]()
Question 9.
Multiply the following polynomials and find the degree of the resultant polynomial:
(i) p(x) = x2 – 9 q(x) = 6x2 + 7x – 2
(ii) f(x) = 7x + 2 g(x) = 15x – 9
(iii) h(x) = 6x2 – 7x + 1 f(x) = 5x – 7
Solution:
(i) p(x) = x2 – 9 q(x) = 6x2 + 7x – 2
p(x) × q(x) = (x2 – 9) (6x2 + 7x – 2)

The required polynomial is 6x4 + 7x3 – 56x2 – 63x + 18, degree 4.
(ii) f(x) = 7x + 2 g(x) = 15x – 9
f(x) × g(x) = (7x + 2) (15x – 9)
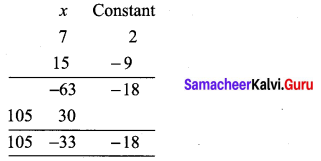
The required polynomial is 105x2 – 33x – 18, degree 2.
(iii) h(x) = 6x2 – 7x + 1 f(x) = 5x – 7
h(x) × f(x) = (6x2 – 7x + 1) (5x – 7)
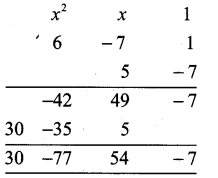
The required polynomial is 30x3 – 77x2 + 54x – 7, degree 3.
Question 10.
The cost of chocolate is Rs. (x + y) and Amir bought (x + y) chocolates. Find the total amount paid by him in terms of x andy. If x = 10, y = 5 find the amount paid by him.
Solution:
Amount paid = Number of chocolates × Cost of a chocolate
= (x + y) (x + y) = (x + y)2 = x2 + 2xy + y2
If x = 10, y = 5
The total amount paid by him
= 102 + 2 × 10 × 5 + 52 = 100 + 100 + 25 = Rs. 225
Question 11.
The length of a rectangle is (3x + 2) units and it’s breadth is (3x – 2) units. Find its area in terms of x. What will be the area if x = 20 units.
Solution:
Area of a rectangle = length × breadth
= (3x + 2) × (3x – 2) = (3x)2 – 22 = [9x2 – 4] Sq. units
If x = 20, Area = 9 × 202 – 4 = 9 × 400 – 4
= 3600 – 4 = 3596 Sq. units
![]()
Question 12.
p(x) is a polynomial of degree 1 and q(x) is a polynomial of degree 2. What kind of the polynomial p(x) × q(x) is ?
Solution:
p(x) is a polynomial of degree 1. q(x) is a polynomial of degree 2.
Then the p(x) × q(x) will be the polynomial of degree (1 + 2) = 3 (or)
Cubic polynomial