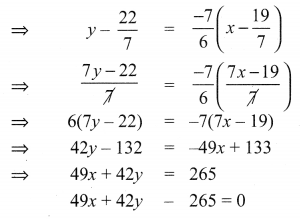You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 5 Coordinate Geometry Unit Exercise 5
Question 1.
PQRS is a rectangle formed by joining the points P(-1, -1), Q(-1, 4) ,R(5, 4) and S(5, -1). A, B, C and D are the mid-points of PQ, QR, RS and SP respectively. Is the quadrilateral ABCD a square, a rectangle or a rhombus? Justify your answer.
Solution:
A, B, C and D are mid points of PQ, QR, RS & SP respectively.
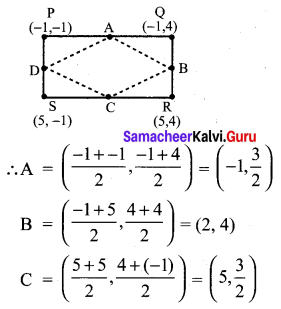

∴ AB and BC are not perpendicular
⇒ ABCD is rhombus as diagonals are perpendicular and sides are not perpendicular.
![]()
Question 2.
The area of a triangle is 5 sq.units. Two of its vertices are (2, 1) and (3, -2). The third Vertex is (x, y) where y = x + 3 . Find the coordinates of the third vertex.
Solution:
Area of triangle formed by points (x1, y1),

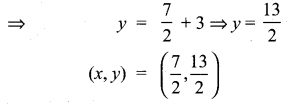
Question 3.
Find the area of a triangle formed by the lines 3x + y – 2 = 0, 5x + 2y – 3 = 0 and 2x – y – 3 = 0
Solution:

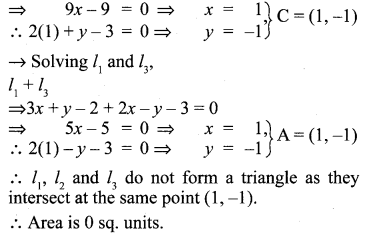
![]()
Question 4.
If vertices of a quadrilateral are at A(-5, 7), B(-4, k) , C(-1, -6) and D(4, 5) and its area is
72 sq.units. Find the value of k.
Area (quadrilateral ABCD)
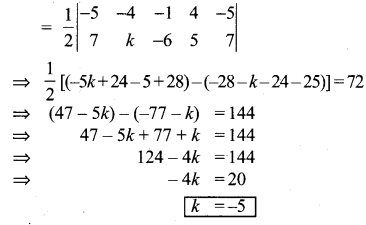
Question 5.
Without using distance formula, show that the points (-2, -1) , (4, 0) , (3, 3) and (-3, 2) are vertices of a parallelogram.
Solution:
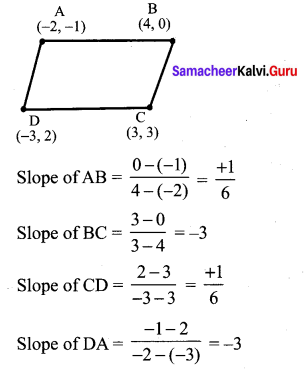
Slope of AB = Slope of CD
Slope of BC = Slope of DA
Hence ABCD forms a parallelogram.
Question 6.
Find the equations of the lines, whose sum and product of intercepts are 1 and -6 respectively.
Let the intercepts be x1, y1 respectively

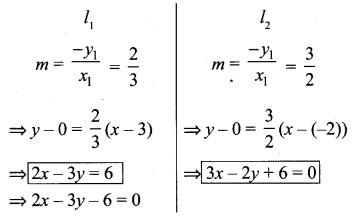
![]()
Question 7.
The owner of a milk store finds that, he can sell 980 litres of milk each week at ₹ 14/litre and 1220 litres of milk each week at ₹ 16 litre. Assuming a linear relationship
between selling price and demand, how many litres could he sell weekly at ₹ 17/litre?
Solution:

Question 8.
Find the image of the point (3, 8) with respect to the line x + 3y = 7 assuming the line to be a plane mirror.
Solution:
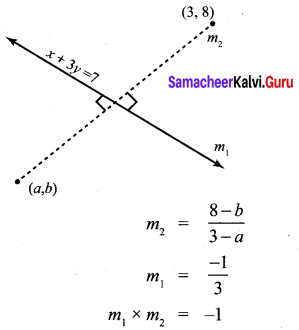
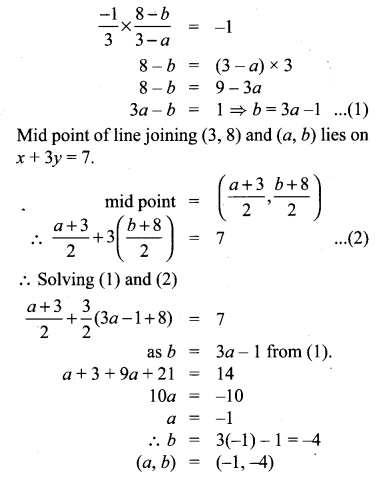
Question 9.
Find the equation of a line passing through the point of intersection of the lines 4x + 7y – 3 = 0 and 2x – 3y + 1 = 0 that has equal intercepts on the axes.
Solution:
4x + 7y – 3 = 0
2x – 3y + 1 = 0
4x + 7y – 3 – 2(2x – 3y + 1) = 0

![]()
Question 10.
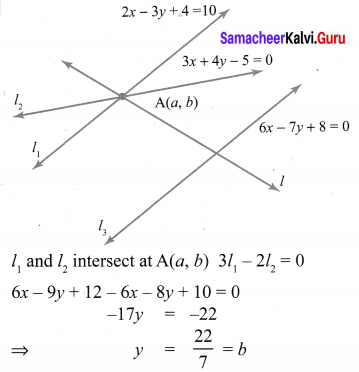
A person standing at a junction (crossing) of two straight paths represented by the equations 2x – 3y + 4 = 0 and 3x + 4y – 5 = 0 seek to reach the path whose equation is 6x – 7y + 8 = 0 in the least time. Find the equation of the path that he should follow.
Solution: