Students can Download Maths Chapter 3 Algebra Ex 3.4 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
![]()
Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 3 Algebra Ex 3.4
Question 1.
Factorise the following by taking out the common factor
(i) 18xy – 12yz
(ii) 9x5y3 + 6x3y2 – 18x2y
(iii) x(b – 2c) + y(b – 2c)
(iv) (ax + ay) + (bx + by)
(v) 2x2(4x – 1) – 4x + 1
(vi) 3y(x – 2)2 – 2(2 – x)
(vii) 6xy – 4y2 + 12xy – 2yzx
(viii) a3 – 3a2 + a – 3
(ix) 3y3 – 48y
(x) ab2 – bc2 – ab + c2
Solution:
(i) 18xy – 12yz = (2 × 3 × 3 × y × x) – (2 × 2 × 3 × y × z)
Taking out the common factors 2, 3, y, we get
= 2 × 3 × y (3x – 2z) = 6y (3x- 2z)
i) 9x5y3 + 6x3y2 – 18x2y = (3 × 3 × x2 × x3 × y × y2) + (2 × 3 × x2 × x × y × y)
Taking out the common factors 3, x2, y, we get
= 3 × x2 × y (3x3 y2 + 2xy – 6)
= 3x2y (3x3 y2 + 2xy – 6)
(iii) x(b – 2c) + y(b – 2c)
Taking out the binomial factor (b – 2c) from each term, we have
= (b – 2c)(x + y)
(iv) (ax + ay) + (bx + by)
Taking at ‘a’ from the first term and ‘b’ from the second term we have
(ax + ay) + (bx + by) = a (x + y) + b (x + y)
Now taking out the binomial factor (x + y) from each term
= (x + y)(a + b)
(v) 2x2(4x – 1) – 4x + 1
Taking out -1 from last two terms
2x2 (4x – 1) – 4x + 1 = 2x2 (4x – 1) – 1 (4x- 1)
Taking out the binomial factor 4x – 1, we get
= (4x – 1)(2x2 – 1)
(vi) 3y(x – 2)2 – 2(2 – x)
3y(x – 2)2 – 2(2 – x) = 3y(x – 2)(x – 2)-2(-1) (x – 2) [∵ Taking out -1 from 2 – x]
= 3y (x – 2) (x – 2) + 2 (x – 2)
Taking out the binomial factor x – 2 from each term, we get
= (x – 2) [3y (x – 2) + 2]
(vii) 6xy – 4y2 + 12xy – 2yzx
= 6xy + 12xy – 4y2 – 2yzx [∵ Addition is commutative]
= (6 × x × y) + (2 × 6 × x × y) + (-1) (2) (2) y + y) + ((-1) (2) (y) (z) (x))
Taking out 6 × x × y from first two terms and (-1) × 2 × y from last two terms we get
= 6 × x × y(1 + 2) + (-1)(2)y[2y + zx]
= 6xy (3) -2y(2y + zx)
= (2 × 3 × 3 × x × y) – 2xy (2y + zx)
Taking out 2y from two terms
= 2y (9x – (2y + zx)) = 2y (9x – 2y – xz)
(viii) a2 – 3a2 + a – 3 = a2 (a – 3) + 1 (a – 3) [∵ Grouping the terms suitably]
= (a – 3) (a2 + 1)
(ix) 3y2 – 48y = 3 × y × y2 – 3 × 16 × y
Taking out 3 × y = 3y (y2 – 16) = 3y (y2 – 42)
Comparing y2 – 42 with a2 – b2
a = y, b = 4
a2 – b2 = (a + b) (a – b)
y2 – 42 = (y + 4) (y – 4)
∴ 3y (y2 – 16) = 3y (y + 4) (y – 4)
(x) ab2 – bc2 – ab + c2
Grouping suitably
ab2 – bc2 – ab + c2 = b ((ab – c2) – 1(ab – c2)
Taking out the binomial factor ab – c2 = (ab – c2) (b – 1)
![]()
Question 2.
Factorise the following expressions
(i) x2 + 14x + 49
(ii) y2 – 10y + 25
(iii) c2 – 4c – 12
(iv) m2 + m – 72
(v) 4x2 – 8x + 3
Solution:
x2 + 14x + 49 = x2 + 14x + 72
Comparing with a2 + 2ab + b2 = (a + b)2 we have a = x and b = 7
⇒ x2 + 2(x) (7) + 72 = (x + 7)2
∴ x2 + 14x + 49 = (x + 7)2
(ii) y2 – 10y + 25 = y2 – 10y + 52
Comparing with a2 – 2ab + b2 = (a – b)2 we get a = y ; b = 5
⇒ y2 – 2(y) (5) + 52 = (y – 5)2
∴ y2 – 10y + 25 = (y – 5)2
(iii) c2 – 4c – 12
This is of the form ax2 + bx + c
Where a = 1,b = – 4 c = – 12, x = c
Now the product ac = 1 × – 12 = – 12 and the sum b = -4

(iv) m2 + m – 72
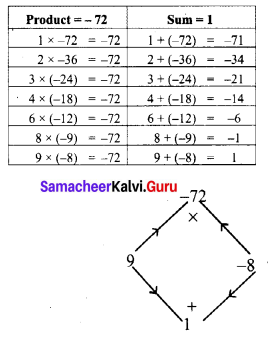
This is of the form ax2 + bx + c
where a = 1, b = 1, c = -12
Product a × c = 1 × -72 = -72
Sum b = 1
The middle term m can be written as 9m – 8m
m2 + m – 72 = m2 + 9m – 8m – 12
= m (m + 9) – 8 (m + 9)
Taking out (m + 9)
= (m + 9) (m – 8)
∴ m2 + m – 72 = (m + 9) (m – 8)
(v) 4x2 – 8x + 3
This is of the form ax2 + bx + c with a = 4 b = -8 c = 3
Product ac = 4 × 3 = 12
Sum b = -8

![]()
Question 3.
Factorize the following expressions using a3 + b3 = (a + b)(a2 – ab + b2) identity
(i) h3 + k2
(ii) 2a3 + 16
(iii) x3y3 + 27
(iv) 64m3 + n3
(v) r4 + 27p3r
Solution:
(i) h3 + k3
Comparing h3 + k3 with a3 + b3 = (a + b)(a2 – ab + b2) we have a = h, b = k
∴ h3 + k3 = (h + k)(h2 – hk + k2)
(ii) 2a2 + 16
(2 × a3) + (2 × 8) = 2(a3 + 8) = 2 (a3 + 23)
∴ 2a3 + 16 = 2 (a3 + 23)
Comparing with a3 + b3 we have a = a and b = 2
a3 + b3 = (a + b)(a2 – ab + b2)
2(a3 + 23) = 2[(a + 2) (a2 – (a) (2) + 22)] = 2[(a + 2) (a2 – 2a + 4)]
2a3 +16 = 2 (a + 2) (a2 – 2a + 4)
(iii) x3 y3 + 27 = (xy)3 + 33
Comparing with a3 + b3 we have a = xy ;b = 3
a3 + b3 = (a + b) (a2 – ab + b2)
(xy)3 + 33 = (xy + 3) ((xy)2 – (xy) (3) + 32) = (xy + 3) (x2y2 – 3xy + 9)
∴ x3y3 + 27 = (xy + 3)(x2y2 – 3xy + 9)
(iv) 64m3 + n3 = (43m3) + n3
= (4m)3 + n3
Comparing this with a3 + b3 we have a = 4m; b = n
a3 + b3 = (a + b) (a2 – ab + b2)
(4m)3 + n3 = (4m + n) [(4m)2 – (4m) (n) + n2]
= (4m + n) [42m2 – 4mn + n2]
= (4m + n) [ 16m2 – 4mn + n2]
64m3 + n3 = (4m + n) (16m2 – 4mn + n2)
(v) r3 + 27p3r = r (r3 + 27p3) = r [r3 + 33p3]
Comparing r3 + (3p)3 with a3 + b3 we have a = r; b = 3p
a3 + b3 = (a + b)(a2 – ab + b2)
r[r3 + (3p)3] = r[(r + 3p)(r2 – r(3p) + (3p)2)]
= r[(r+ 3p) (r2 – 3rp + 32p2]
= r(r + 3p) (r2 – 3rp + 9p2)
r4 + 27p3r = r(r + 3p) (r2 – 3rp + 9p2)
Question 4.
Factorize the following expressions using a3 – b3 = (a – b)(a2 + ab + b2) identity
(i) y3 – 27
(ii) 3b3 – 192c3
(iii) -16y3 + 2x3
(iv) x3 y3 – 73
(v) c3 – 27b3 a3
Solution:
(i) y3 – 27 = y3 – 33
Comparing this with a3 – b3 , we have a = y and b = 3
a3 – b3 = (a + b) (a2 + ab + b2 )
y3 – 33 = (y – 3)(y2 + (y) (3) + 32 ) = (y – 3) (y2 + 3y + 9)
y3 – 27 = (y – 3) (y2 + 3y + 9)
(ii) 3b3 + 192c3 = (3 × b3) – (3 × 4 × 4 × 4 × c3) = 3(b3 – 43 c3)
= 3(b3 – (4c)3 )
Comparing b3 – (4c)3 with a3 – b3 we have a = b and b = 4c
a3 – b3 = (a – b) (a2 + ab + b2)
3(b3 – (4c)3) = 3[(b – 4c)(b2 + (b)(4c) + (4c)2)]
= 3[(b – 4c)(b2 + 4bc + 42 c2)]
3b3 – 192c3 = 3 [(b – 4c) (b2 + 4bc + 16c2)]
(iii) -16y3 + 2x3 = 2x3 – 16y3 [∵ Addition is commatative]
= 2(x3 – 8y3) = 2(x3 – 23y3)
= 2(x3 – (2y)3)
Comparing x3 – (2y)3 with a3 – b3 we have a = x and b = 2y
a3 – b3 = (a – b)(a2 + ab + b2)
2[x3 – (2y)3] = 2[(x – 2y) (x2 + (x) (2y) + (2y)2)]
= 2[(x – 2y) (x2 + 2xy + 22 y2)]
-16y3 + 2x3 = 2[(x – 2y)(x2 + 2xy + 4y2)]
(iv) x3y3 – 73 = (xy)3 – 73
Comparing with a3 – b3 we have a = xy and b = 7
a3 – b3 = (a – b)(a2 + ab + b2)
(xy)3 – 73 = (xy – 7) ((xy)2 + (xy) (7) + 72)
x3y3 – 73 = (xy – 7) (x2y2 + 7xy + 49)
(v) c3 – 27 b3 a3 = c3 – 33b3 a3 = c3 – (3ba)3
Comparing this with a3 – b3 we have a = x and b = 3ba
a3 – b3 = (a – b)(a2 + ab + b2)
∴ c3 – (3ba)3 = (c – 3ba) (c2 + (c) (3ba) + (3ba)2)
= (c – 3ba) (c2 + 3bac + 32 b2a2)
c3 – 27b3a3 = (c – 3ab) (c2 + 3bac + 9a2b2)