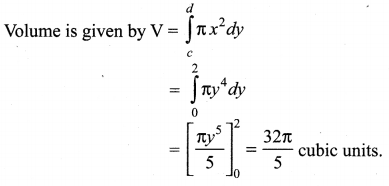You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 9 Applications of Integration Ex 9.9
Question 1.
Find, by integration, the volume of the solid generated by revolving about the x-axis, the region enclosed by y = 2x2, y = 0 and x = 1.
Solution:

Question 2.
Find, by integration, the volume of the solid generated by revolving about the x-axis, the region enclosed by y = e-2x y = 0, x = 0 and x = 1.
Solution:

![]()
Question 3.
Find, by integration, the volume of the solid generated by revolving about the y-axis, the region enclosed by x2 = 1 + y and y = 3.
Solution:

Question 4.
The region enclosed between the graphs of y = x and y = x2 is denoted by R, Find the volume generated when R is rotated through 360° about x – axis.
Solution:
To find points of intersection, solving y = x2 and y = x, we get (0, 0) and (1, 1)
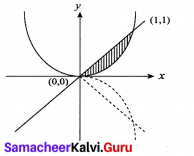
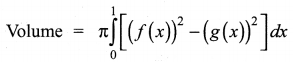
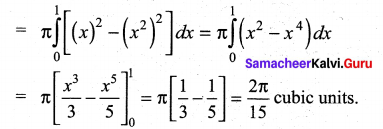
![]()
Question 5.
Find, by integration, the volume of the container which is in the shape of a right circular conical frustum as shown in the Figure.
Solution:

Question 6.
A watermelon has an ellipsoid shape which can be obtained by revolving an ellipse with major-axis 20 cm and minor-axis 10 cm about its major-axis. Find its volume using integration.
Solution:
From the given data a = 10 cm and b = 5 cm
Equation of the Ellipse
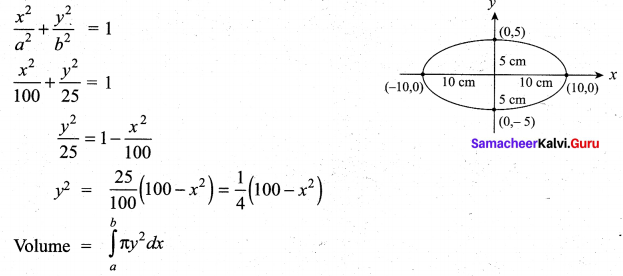
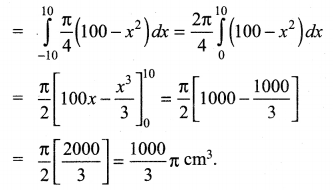
Samacheer Kalvi 12th Maths Solutions Chapter 9 Applications of Integration Ex 9.9 Additional Questions
Question 1.
Find the volume of the solid that results when the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) (a > b > 0) is revolved about the minor axis.
Solution:
Volume of the solid is obtained by revolving the right side of the curve \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) about the y-axis.
Limits for y is obtained by putting x = 0 ⇒ y2 = b2 ⇒ y = ±b.
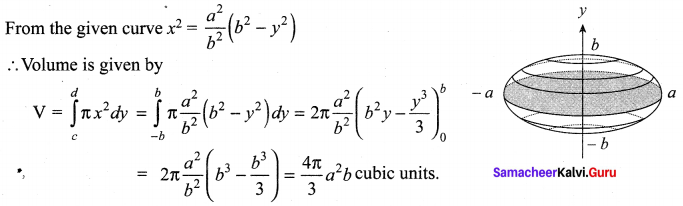
![]()
Question 2.
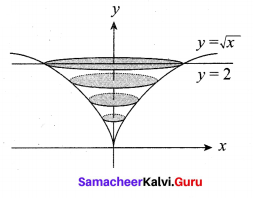
Find the volume of the solid generated when the region enclosed by y = \(\sqrt{x}\), y = 2 and x = 0 is revolved about the y – axis.
Solution:
Since the solid is generated by revolving about the y-axis, rewrite y = \(\sqrt{x}\) as x = y2.
Taking the limits for y, y = 0 and y = 2 (Putting x = 0 in x = y2, we get y = 0)