You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.2
Question 1.
Solve for x.
(i) |3 – x| < 7
Solution:
– 7 < 3 – x < 7
– 7 – 3 < – x < 7 – 3
– 10 < – x < 4 10 > x > – 4
– 4 < x < 10
∴ The solution set is x ∈ (-4, 10)
(ii) |4x – 5| ≥ -2
Solution:
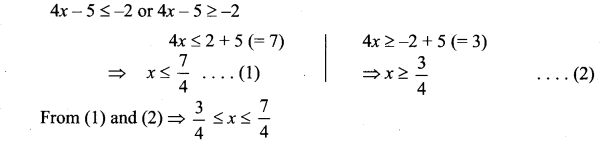
(iii)
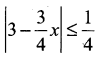
Solution:
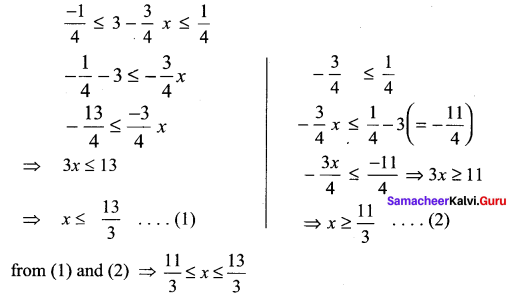
(iv) |x| – 10 < -3
Solution:
|x| < -3 + 10 (= 7)
|x| < 7 ⇒ -7 < x < 7
![]()
Question 2.
Solve \(\frac{1}{|2 x-1|}<6\) and express the solution using the interval notation.
Solution:

Question 3.
Solve -3|x| + 5 ≤ – 2 and graph the solution set in a number line.
Solution:
-3 |x| + 5 ≤ – 2
-3 |x| ≤ – 2 – 5
-3 |x| ≤ – 7
3 |x| ≥ 7
|x| ≥ \(\frac{7}{3}\)
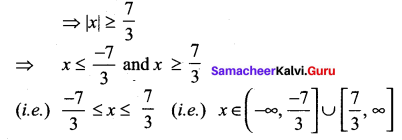
![]()
Question 4.
Solve 2|x + 1| – 6 ≤ 7 and graph the solution set in a number line.
Solution:

Question 5.
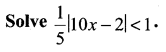
Solution:
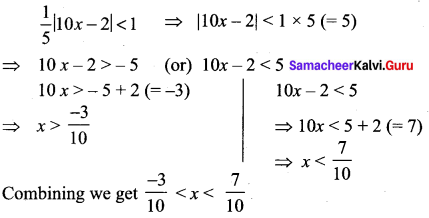
![]()
Question 6.
Solve |5x – 12| < -2
Solution:

Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.2 Additional Questions
Question 1.
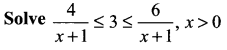
Solution:

Question 2.
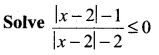
Solution:
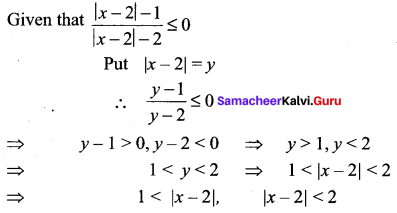
⇒ x – 2 < – 1 (or) x – 2 > 1 and – 2 < x – 2 < 2
⇒ x < 1 (or) x > 3 and -2 + 2 < x < 2 + 2
⇒ x < 1 (or) x > 3 and 0 < x < 4 Hence, the required solution is (0, 1) ∪ (3, 4)
![]()
Question 3.
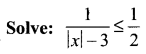
Solution:

Question 4.
Solve: |x – 1| ≤ 5, |x| ≥ 2
Solution:
|x – 1| ≤ 5 and |x| ≥ 2
⇒ -5 ≤ x – 1 ≤ 5 and x ≤ -2 (or) x > 2
⇒ – 5 + 1 ≤ x ≤ 5 + 1
⇒ -4 ≤ x ≤ 6 and x ≤ -2 (or) x ≥ 2
Hence x < [-4, -2] ∪ [2, 6]
![]()
Question 5.
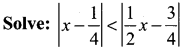
Solution:
