Samacheer Kalvi 12th Maths Solutions Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.2

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.2

Question 1.
Find the equation of the parabola in each of the cases given below:
(i) focus (4, 0) and directrix x = – 4.
(ii) passes through (2, -3) and symmetric about y-axis.
(iii) vertex (1, – 2) and focus (4, – 2).
(iv) end points of latus rectum(4, – 8) and (4, 8) .
Solution:
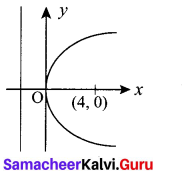
(i) Focus = F = (4, 0)
⇒ a = 4
Equation of directrix x = – 4
⇒ The curve open to the right. So the equation will be of the form y² = 4 ax
Here a = 4
⇒ y² = 4 (4) x (i.e.,)y² = 16x

(ii) The parabola is symmetric about y axis. So the equation will be of the form
In given data the parabola is open downwards, vertex be (0, 0)
Equation of parabola x² = -4ay
It passes through point (2, -3)
4 = -4a (-3)
1 = 3a
a = \(\frac {1}{3}\)
∴ Equation of parabola
x² = -4(\(\frac {1}{3}\)) y
3x² = -4y

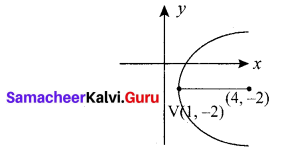
(iii) The distance between vertex and focus = 3
(ie.,) a = 3
Parabola is open to the right.
So equation will be of the form y² = 4ax
Here a = 3 ⇒ y² = 12x
but the vertex is (1, -2)
So equation of the parabola is
(y + 2)² = 12(x – 1)

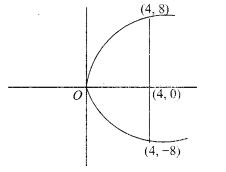
(iv) Equation of parabola
y² = 4ax
a = VS = 4
y² = 4(4)x
y² = 16x

Question 2.
Find the equation of the ellipse in each of the cases given below:
(i) foci (± 3, 0), e = \(\frac{1}{2}\)
(ii) foci (0, ± 4) and end points of major axis are(0, ± 5).
(iii) length of latus rectum 8, eccentricity = \(\frac{3}{5}\) and major axis on x -axis.
(iv) length of latus rectum 4 , distance between foci \(4 \sqrt{2}\) and major axis as y -axis.
Solution:
(i) Given ae = 3 and e = \(\frac{1}{2}\)
⇒ a(\(\frac{1}{2}\)) = 3 ⇒ a = 6
So a² = 36
b² = a²(1 – e²) = 36 (1 – \(\frac{1}{4}\)) = 36 × \(\frac{3}{4}\) = 27
Since Foci = (± 3, 0), major axis is along x-axis
So equation of ellipse is \(\frac{x^{2}}{36}+\frac{y^{2}}{27}\) = 1

(ii) From the diagram we see that major axis is along y-axis.

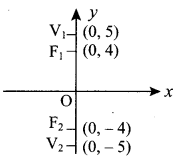
Also a = 5 and ae = 4
⇒ 5e = 4 ⇒ e = \(\frac{4}{5}\)
Now a = 5 ⇒ a² = 25
ae = 4 ⇒ ae² = 16
We know b² = a² (1 – e²) = a² – a²e² = 25 – 16 = 9
Equation of ellipse is \(\frac{x^{2}}{9}+\frac{y^{2}}{25}\) = 1

(iv) Distance between foci = 4√2
2ae = 4√2
ae = 2√2
Length of latus rectum = 4
\(\frac {2b^2}{a}\) = 4
b² = 2a
b² = a²(1 – e²)
2a = a² – a² e²
2a = a² – (2√2)²
⇒ a² – 8 – 2a = 0
(a – 4) (a + 2) = 0
a = 4 & a = -2 (Not possible)
∴ a = 4 ⇒ a² = 16
b² = 2a = 2(4) = 8
\(\frac {x^2}{b^2}\) + \(\frac {y^2}{a^2}\) = 1
\(\frac {x^2}{8}\) + \(\frac {y^2}{16}\) = 1

Question 3.
Find the equation of the hyperbola in each of the cases given below:
(i) foci (± 2, 0), eccentricity = \(\frac{3}{2}\)
(ii) Centre (2,1), one of the foci (8,1) and corresponding directrix x = 4 .
(iii) passing through(5, -2) and length of the transverse axis along JC axis and of length 8 units.
Solution:
(i) Given
ae = 2 and e = \(\frac{3}{2}\)
a( \(\frac{3}{2}\)) = 2 ⇒ a = \(\frac{4}{3}\) So a² = \(\frac{16}{9}\)
b² = a²(e² – 1) = a² e² – a² = 4 – \(\frac{16}{9}\) = \(\frac{20}{9}\)
Since the foci are (± 2, 0), transverse axis is along x-axis
So equation of hyperbola is
\(\frac{x^{2}}{16 / 9}-\frac{y^{2}}{20 / 9}\) = 1 ⇒ \(\frac{9 x^{2}}{16}-\frac{9 y^{2}}{20}\) = 1

(ii) Given Centre = (2, 1)
ae = 6 (distance between (2, 1) and (8, 1)) ……………. (1)
Also \(\frac{a}{e}\) = 2 ⇒ a = 2e
Equation of directrix is x = 4 [(i.e.,) (x – 2 = 2) Since centre is (2, 1)]
⇒ \(\frac{a}{e}\) = 2
Given ae = 6 ⇒ a² e² = 36
(i.e.) (2e)² (e)² = 36
⇒ 4e⁴ = 36 ⇒ e⁴ = 9
⇒ e = \(\sqrt{3}\)
Now e = \(\sqrt{3}\) a = \(2\sqrt{3}\)
∴ a² = 4 × 3 = 12
b² = a² (e² – 1) = a² e² – a² = 36 – 12 = 24
So here Centre = (2, 1)
So equation of hyperbola is
\(\frac{(x-2)^{2}}{12}-\frac{(y-1)^{2}}{24}\) = 1

(iii) Length of the transverse axis = 8
2a = 8 ⇒ a = 4
The transverse axis is along the x-axis
So of the equation of the hyperbola is will be

Question 4.
Find the vertex, focus, equation of directrix and length of the latus rectum of the following:
(i) y² = 16x
(ii) x² = 24y
(iii) y² = -8x
(iv) x² – 2x + 8y + 17 = 0
(v) y² – 4y – 8x + 12 = 0
Solution:
(i) y² = 16x
It is of the form y² = 4ax (type I)
Here 4a = 16 ⇒ a = 4
Vertex = (0, 0)
Focus = (a, 0) = (4, 0)
Equation of directrix x + 4 = 0 (or) x = – 4
Length of latus rectum = 4a = 16 .

(ii) x² = 24y
This is of the form x² = 4ay (type III)
4a = 24 ⇒ a = 6
Vertex = (0, 0)
Focus = (0, a) = (0, 6)
Equation of directrix is y + a= 0 (i.e.,) y + 6 = 0 (or) y = -6
Length of latus rectum = 4a = 24.

(iii) y² = -8x
This is of the form y² = – 4ax (type II)
Here 4a = 8 ⇒ a = 2
Vertex = (0, 0)
Focus = (- a, 0) = (-2, 0)
Equation of directrix is x – 2 = 0 (or) x = 2
Length of latus rectum = 4a = 8.

(iv) x² – 2x + 8y + 17 = 0
x² – 2x = -8y – 17
x² – 2x + 1 – 1 = – 8y — 17
(x – 1)² = – 8y – 17 + 1 = – 8y + 16
(x – 1)² = – 8 (y – 2)
Taking x – 1 = X and y – 2 = Y.
We get X² = – 8Y.
This is of the form x² = – 4ay (type IV)
Where 4a = 8 ⇒ a = 2

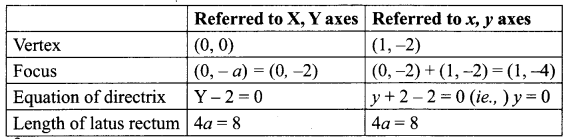
(v) y² – 4y = 8x – 12 = 0
y² – 4y + 4 = 8x – 12 + 4
(y – 2)² = 8x – 8 = 8 (x – 1)
Taking x – 1 = X and y – 2 = Y.
We get Y² = 8X.
This is of the form y² = 4ax (type IV)
Where 4a = 8 ⇒ a = 2

Question 5.
Identify the type of conic and find centre, foci, vertices, and directrices of each of the following:

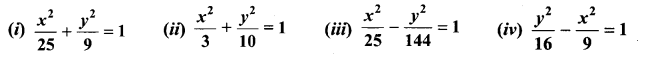
Solution:
(i) \(\frac {x^2}{25}\) + \(\frac {y^2}{9}\) = 1
It is an ellipse and the major axis is along x-axis.
a² = 25; b² = 9
a = 5; b = 3
c² = a² – b²
= 25 – 9 = 16
c = 4
ae = 4
⇒ 5e = 4
e = \(\frac {4}{5}\)
Centre = (0, 0)
Vertex (±a, 0) = (±5, 0)
Foci (±c, 0) = (±4, 0)
Equation of directrix
x = ±\(\frac {a}{e}\) = ±\(\frac {5}{\frac{4}{5}}\) = ±\(\frac {25}{4}\)

(ii) \(\frac{x^{2}}{3}+\frac{y^{2}}{10}\) = 1
It is an ellipse and here (always a >b)

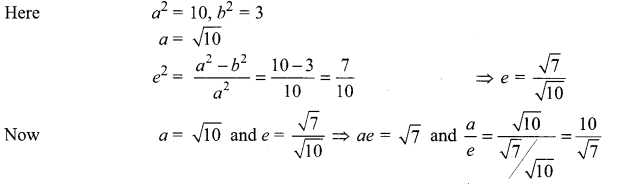
Here the major axis is along y-axis
Centre = (0, 0)
Foci = (0, ± ae) = (0, ± \(\sqrt{7}\))
Vertices = (0, ± a) = (0, ± \(\sqrt{10}\) )
Equation of directrices y = ± \(\frac{10}{\sqrt{7}}\)

(iii) \(\frac{x^{2}}{25}-\frac{y^{2}}{144}\) = 1

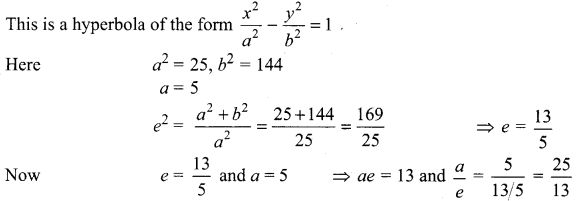
Now, Here transverse axis is along x-axis
Centre = (0, 0)
Vertices = (± a, 0) = (± 5, 0)
Foci = (± ae, 0) = (± 13, 0)
Equation of directrices x = ± \(\frac{a}{e}\) (ie.,) x = ± \(\frac{25}{13}\)

(iv) \(\frac{y^{2}}{16}-\frac{x^{2}}{9}\) = 1
It is a hyperbola. Here transverse axis is along y-axis

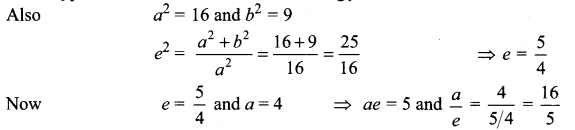
Now Centre = (0, 0)
Vertices = (0, ± a) = (0, ± 4)
Foci = (0, ± ae) = (0, ± 5)
Equation of directrices y = ± \(\frac{16}{5}\)

Question 6.
Prove that the length of the latus rectum of the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 is \(\frac{2 b^{2}}{a}\)
Solution:
The latus rectum LL’ of the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 passes through the focus(ae, 0)

Question 7.
Show that the absolute value of the difference of the focal distances of any point P on the hyperbola is the length of its transverse axis.
Solution:

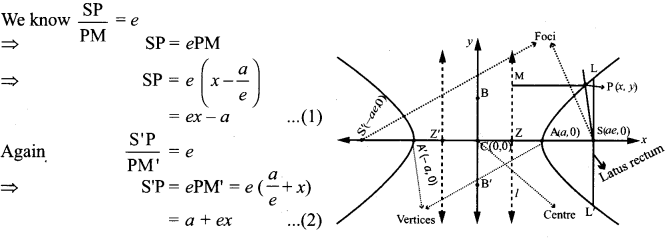
∴ S’P – SP = (a + ex) – (ex – a)
a + ex – ex + a = 2a (transverse axis)

Question 8.
Identify the type of conic and find centre, foci, vertices, and directrices of each of the following:

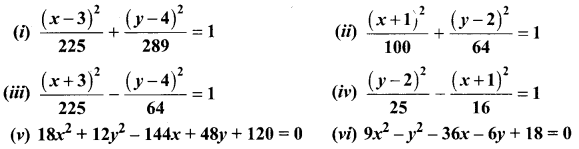
Solution:

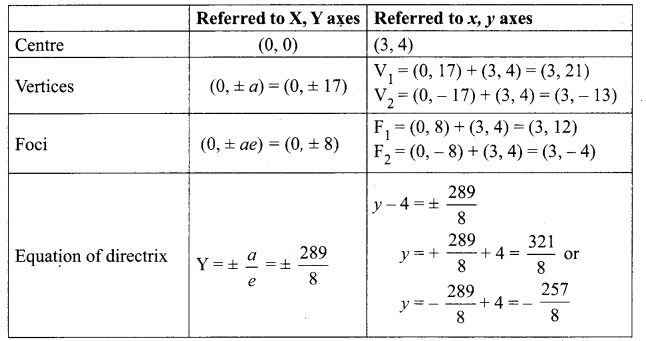
(v) 18x² + 12y² – 144x + 48y + 120 = 0
(18x² – 144x) + (12y² + 48y) = -120
18(x² – 8x) + 12 (y² + 4y) = -120
18(x² – 8x + 16 – 16) + 12(y² + 4y + 4 – 4) = -120
18(x – 4)² – 288 + 12(y + 2)² – 48 = – 120
18(x – 4)² + 12(y + 2)² = -120 + 288 + 48 = 216

Samacheer Kalvi 12th Maths Solutions Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.2 Additional Problems

Question 1.
Find the equation of the ellipse if centre is (3, – 4), one of the foci is (3 + \(\sqrt{3}\), – 4) and e = \(\frac{\sqrt{3}}{2}\)
Solution:

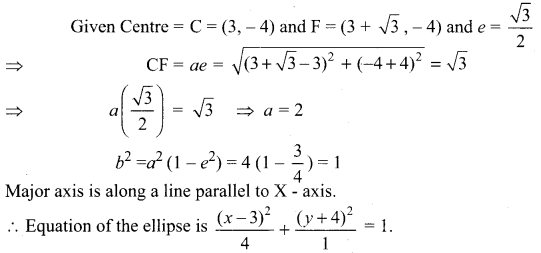
Question 2.
Find the equation of the hyperbola if centre (1, -2); length of the transverse axis is 8; e = \(\frac{5}{4}\) and the transverse axis is parallel to X-axis.
Solution:

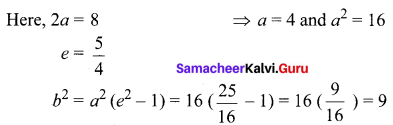
Here, centre = (1, -2) and transverse axis is parallel to X-axis.

Question 3.
Find axis, vertex, focus and equation of directrix for y² + 8x – 6y + 1 = 0
Solution:
y² – 6y = – 8x – 1
y² – 6y + 9 = – 8x – 1 + 9
(y – 3)² = – 8x + 8 = – 8(x – 1)

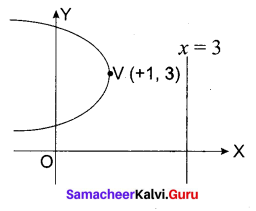
Comparing this equation with Y² = – 4aX we get
4a = 8 or a = 2
Vertex is (0, 0)
x – 1 = 0 ⇒ x = 1, y – 3 = 0 ⇒ y = 3
Axis y – 3 = 0, Vertex = (1, 3)
Focus is (- a, 0) = (-2, 0) + (1, 3) = (-1, 3)
Equation of directrix is x – a = 0. i.e., X – 2 = 0
⇒ x – 1 – 2 = 0 ⇒ x – 3 = 0
Latus rectum x + a = 0 i.e., x – 1 + 2 = 0
x + 1 = 0
Length of latus rectum = 4a = 8

Question 4.
Find axis, Vertex focus and equation of directrix for x² – 6x – 12y – 3 = 0.
Solution:
x² – 6x = 12y + 3
x² – 6x + 9 = 12y + 3 + 9 = 12y + 12
(x – 3)² = 12(y + 1)

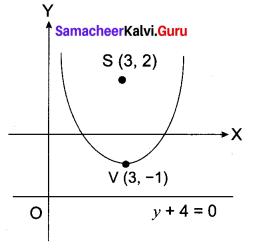
This equation is of the form X² = 4aY
4a = 12
⇒ a = 3
Vertex is x – 3 = 0 ; y + 1 = 0
⇒ x = 3 ; y = -1

Question 5.
Find the eccentricity, centre, foci and vertices of the following hyperbolas: x² – 4y² – 8x – 6y – 18 = 0
Solution:

Question 6.
Find the eccentricity, centre, foci, vertices of 9x² + 4y² = 36
Solution:

Question 7.
Find the eccentricity, centre, foci and vertices of the following hyperbolas:
x² – 4y² + 6x + 16y – 11 = 0
Solution:

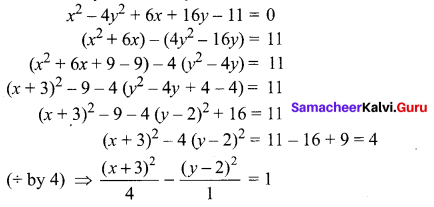
Question 8.
Find the eccentricity, centre, foci and vertices of the following hyperbolas:
x² – 3y² + 6x + 6y + 18 = 0
Solution: