Students can download 12th Business Maths Chapter 10 Operations Research Additional Problems and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 10 Operations Research Additional Problems
I. One Mark Questions
Choose the correct Answer
Question 1.
Which of the following methods is used to verify the optimality of the current solution of the transportation problem?
(a) Least cost method
(b) Vogel’s method
(c) North-west comer rule
(d) None of these
Answer:
(a) Least cost method
Question 2.
The degeneracy’in the transportation problem indicates that _________
(a) Dummy allocations need to be added
(b) The problem has no feasible solution
(c) Multiple optimal solutions exist
(d) All of the above
Answer:
(c) Multiple optimal solutions exist
![]()
Question 3.
The Hungarian method can also be used to solve ______
(a) Transportation problem
(b) Travelling salesman problem
(c) A linear programming problem
(d) All the above
Answer:
(b) Travelling salesman problem
Question 4.
An optimal solution of an assignment problem can be obtained only if, _________
(a) each row and column has only one zero element
(b) each row and column has at least one zero element
(c) The data is arranged in a square matrix
(d) None of the above
Answer:
(d) None of the above
![]()
Question 5.
Say True or False.
- In a transportation problem, a single source may supply something to all destinations.
- A transportation model must have the same number of rows and columns.
- It is usually possible to find an optimal solution to a transportation problem that is degenerate.
- In a transportation problem, a dummy source is given a zero cost, while in an assignment problem, a dummy source is given a very high cost.
- The Hungarian method operates on the principle of matrix reduction, whereby the cost table is reduced to a set of opportunity costs.
Answer:
- True
- False
- True
- False
- True
Question 6.
Fill in the blanks.
- In a transportation problem, we must make the number of ________ and _______ equal.
- ______ or ______ are used to balance an assignment problem.
- The method of finding an initial solution based on opportunity costs is called _______
- ________ occurs when the number of occupied squares is less than the number of rows plus the number of columns minus one.
- Both transportation and assignment problems are members of a category of LP problems called ________
- In the case of an unbalanced problem, shipping cost coefficients of ______ are assigned to each dummy factory or warehouse.
Answer:
- units supplied, units demanded
- Dummy rows, dummy columns
- Vogel’s approximation method
- Degeneracy
- Network flow problems
- zero
![]()
Question 7.
Match the following.
| (a) Dummy column | (i) Finding initial solution |
| (b) Northwest comer rule | (ii) Rows ≠ Columns |
| (c) Hungarian method | (iii) Supply ≠ Demand |
| (d) Feasible solution | (iv) Assignment problem |
| (e) Unbalanced problem | (v) All demand and supply constraints are met |
Answer:
(a) – (iii)
(b) – (i)
(c) – (iv)
(d) – (v)
(e) – (ii)
Question 8.
The objective function of transportation problem is to ________
(a) Maximise total cost
(b) Minimise the total cost
(c) Total cost should be zero
(d) All the above
Answer:
(b) Minimise the total cost
![]()
Question 9.
In transportation problem, optimal solution can be verified by using _______
(a) NWC
(b) LCM
(c) MODI method
(d) Matrix method
Answer:
(c) MODI method
Question 10.
The cells in the transportation problem can be classified as _______
(a) assigned cells and empty cells
(b) allocated cells and unallocated cells
(c) occupied and unoccupied cells
(d) assigned and unoccupied cells
Answer:
(c) occupied and unoccupied cells
![]()
Question 11.
In transportation problem if total supply > total demand we add _________
(a) dummy row with cost 0
(b) dummy column with cost 0
(c) dummy row with cost 1
(d) dummy column with cost 1
Answer:
(b) dummy column with cost 0
Question 12.
In an LPP the objective function is to be ________
(a) Minimised
(b) Maximised
(c) (a) or (b)
(d) only (b)
Answer:
(c) (a) or (b)
![]()
Question 13.
The method used for solving an assignment problem is called ________
(a) Reduced matrix method
(b) MODI method
(c) Hungarian method
(d) Graphical method
Answer:
(c) Hungarian method
II. 2 Mark Questions
Question 1.
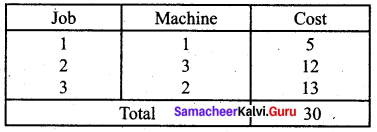
Consider 3 jobs to be assigned to 3 machines. The cost for each combination is shown in the table below. Find the minimal job machine combinations.
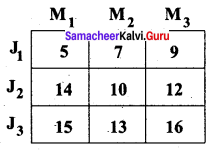
Solution:
Step 1:
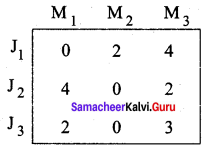
Step 2:
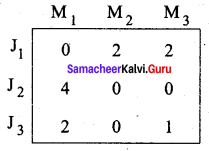
Step 3: (Assignment)
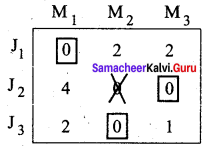
Optimal assignment:
Question 2.
Find an initial basic feasible solution by LCM.
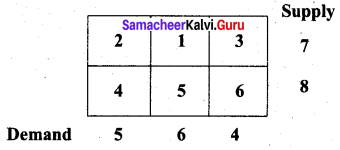
Solution:
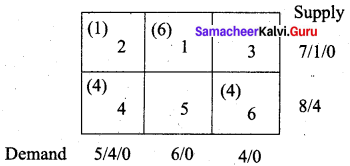
Total cost = (1 × 2) + (6 × 1) + (4 × 4) + (4 × 6)
= 2 + 6 + 16 + 24
= 48
![]()
Question 3.
Find an initial basic feasible solution by the North West Corner Rule (NWC).
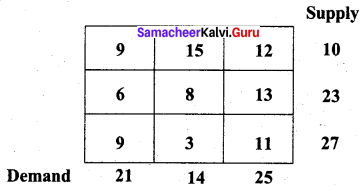
Solution:
Total demand = Total supply = 60
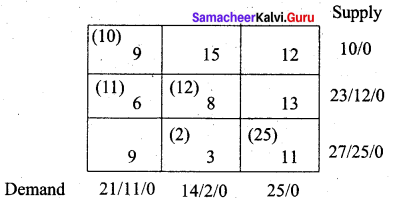
Total cost = (10 × 9) + (11 × 6) + (12 × 8) + (2 × 3) + (25 × 11)
= 90 + 66 + 96 + 6 + 275
= 533
Question 4.
Find an initial basic feasible solution using Least cost method.
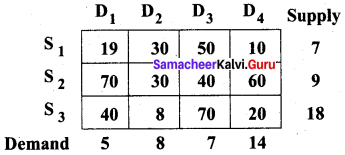
Solution:
Total Demand = 5 + 8 + 7 + 14 = 34
Total Supply = 7 + 9 + 18 = 34
Since they are equal, problem is balanced.
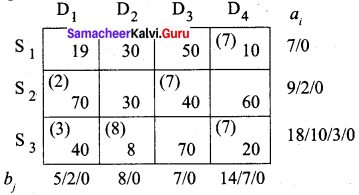
The minimum total transportation cost is = (7 × 10) + (2 × 70) + (7 × 40) + (3 × 40) + (8 × 8) + (7 × 20)
= 70 + 140 + 280 + 120 + 64 + 140
= Rs. 814
![]()
Question 5.
Find the investment option using Maximin rule for the following:
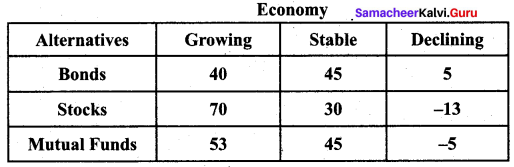
Solution:
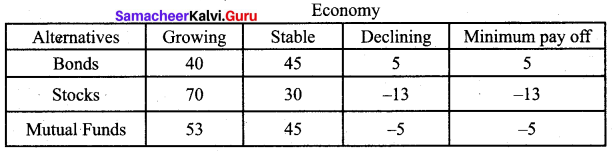
Max (5, -13, -5) = 5. Since the maximum payoff is 5, by maximin criteria, the decision is to invest in bonds.
III. 3 and 5 Marks Questions
Question 1.
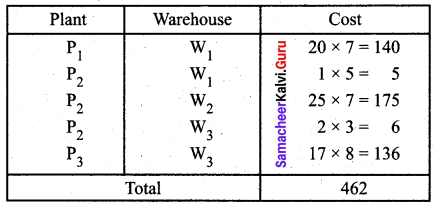
Find an optimal solution to the following transportation problem by North West Corner Method.
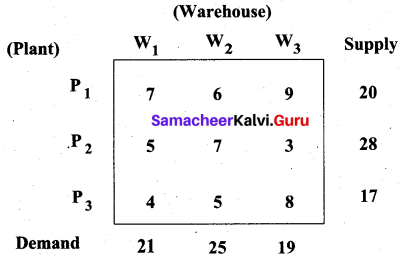
Solution:
Total supply = 65 = Total demand. So the given problem is balanced.
First allocation:
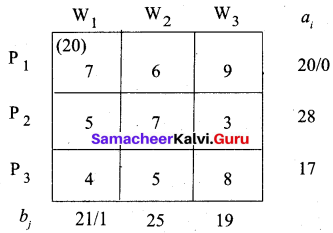
Second allocation:
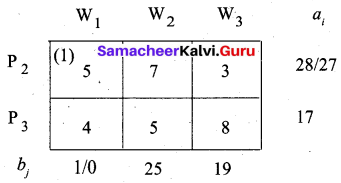
Third allocation:
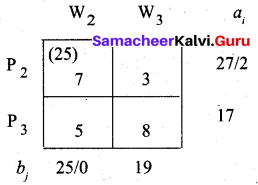
Fourth allocation:
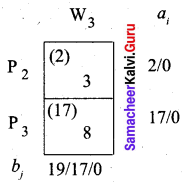
Total Transportation cost
Question 2.
Find an initial basic solution for the following transportation problem by Vogel’s Approximation method.
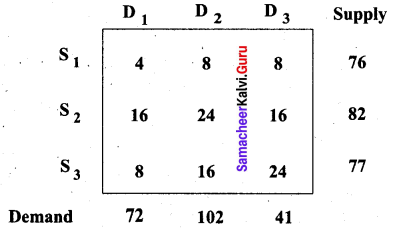
Solution:
Total demand = 72 + 102 + 41 = 215 and
Total supply = 76 + 82 + 77 = 235.
Total supply > Total demand. So we add a dummy constraint with 0 unit cost and with allocation 20 (235 – 215). The modified table is
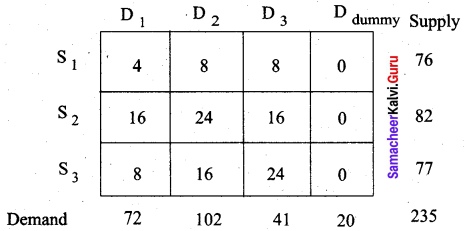
First allocation:
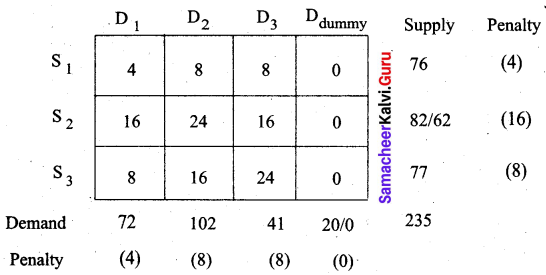
The maximum penalty is 16. Allot 20 units to cell (S2, Ddummy)
Second allocation:
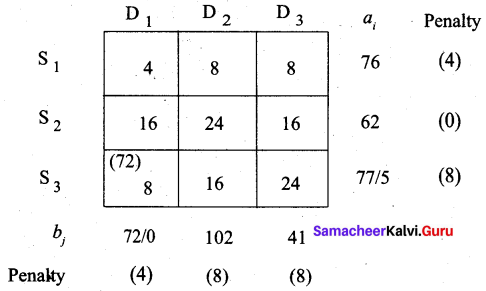
Third allocation:
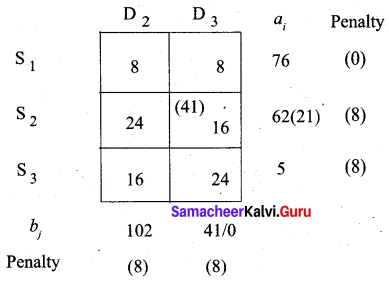
Fourth allocation:
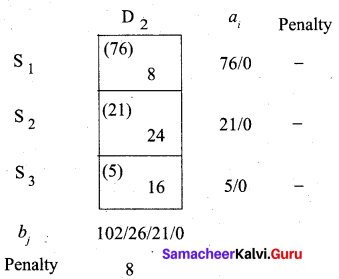
The final allocation table is given below.
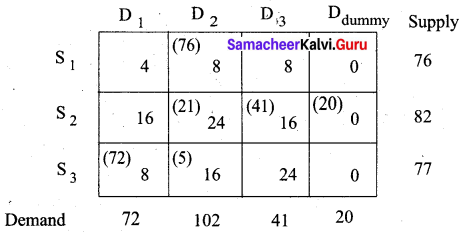
The minimum total cost = (76 × 8) + (21 × 24) + (41 × 16) + (20 × 0) + (72 × 8) + (5 × 16) = 2424
![]()
Question 3.
A company has 4 men available for 4 separate jobs. Only one man can work on anyone job. The cost of assigning each man to each job is given below. Find the optimal solution by the Hungarian method.
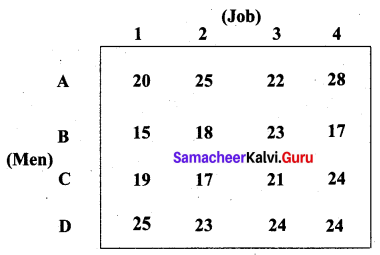
Solution:
The number of rows and columns are equal. So the given problem is a balanced assignment problem and we can get an optimal solution.
Step 1:
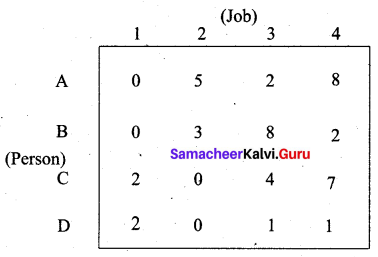
Step 2:
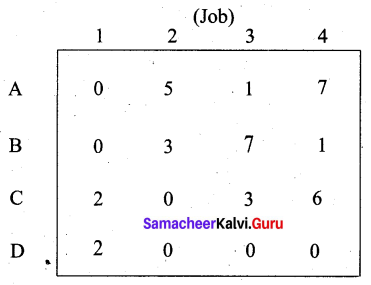
Step 3: (Assignment)
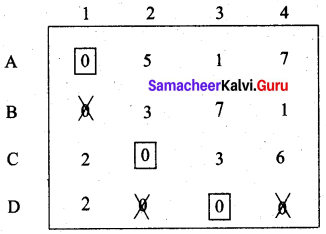
We are not able to assign job for person B. Proceed as follows. Draw a minimum number of vertical and horizontal lines to cover all the zeros.
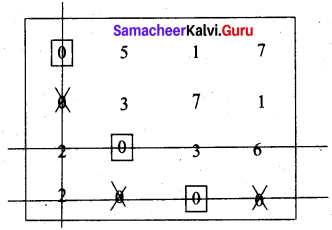
Subtract the smallest element 1 from all the uncovered elements and add it to the elements which lie at the intersection of two lines. Thus we obtain another reduced matrix for fresh assignment.
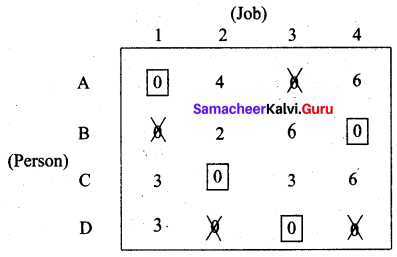
Total cost is
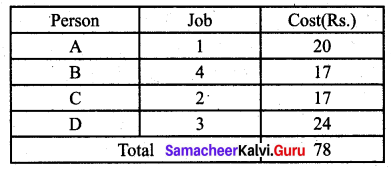
Question 4.
There are five machines and five jobs are to be assigned and the cost matrix is given below. Find the proper assignment.
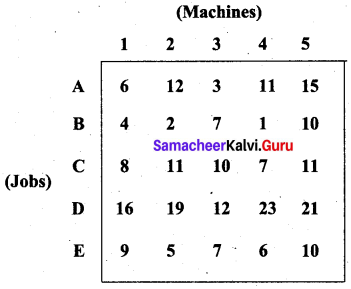
Solution:
Step 1: (Row-reduction)
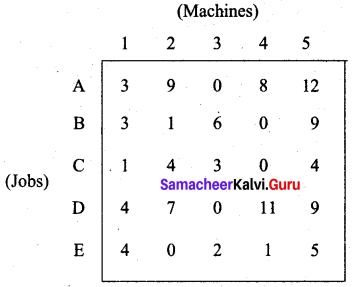
Step 2: (Column – reduction)
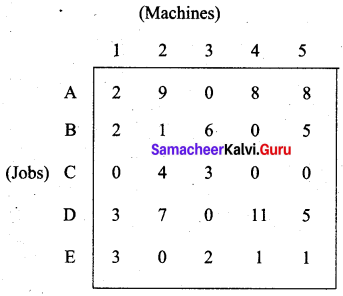
Step 3: (Assignment)
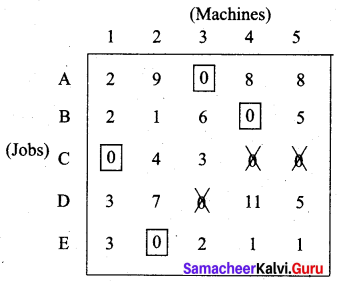
We are not able to assign a machine to job D. We proceed as follows.
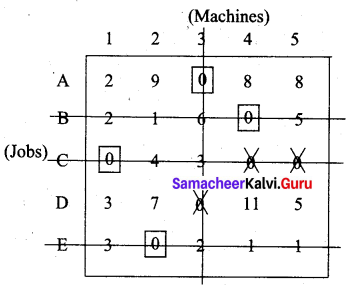
The smallest uncovered element is 2. Subtract 2 from all those elements which are not covered. Add 2 all elements which are at the intersection of two lines. Then proceed with the new matrix.
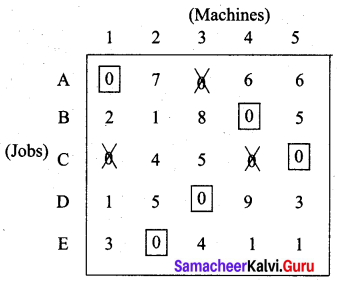
The assignment is as follows
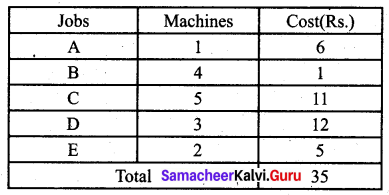
![]()
Question 5.
The cost of transportation from 3 sources to four destinations are given in the follow¬ing table. Obtain an initial basic feasible solution using
(i) North West Corner Rule (NWC)
(ii) Least Cost Method (LCM) and
(iii) Vogel’s Approximation Method (VAM)
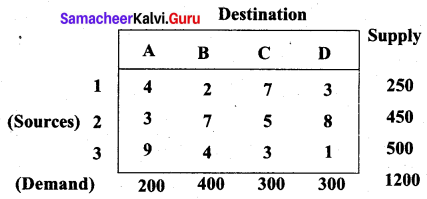
Solution:
(i) North West Corner Rule
We start by allotting the units to the North -West Comer cell. We show all the allocations in a single table.
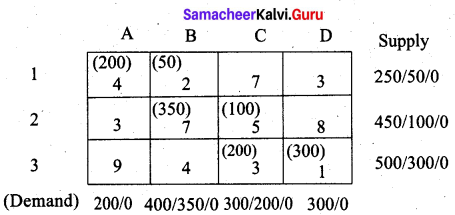
Total transportation cost is (200 × 4) + (50 × 2) + (350 × 7) + (100 × 5) + (200 × 3) + (1 × 300)
= 800 + 100 + 2450 + 500 + 600 + 300
= Rs. 4750
(ii) Least cost method (LCM)
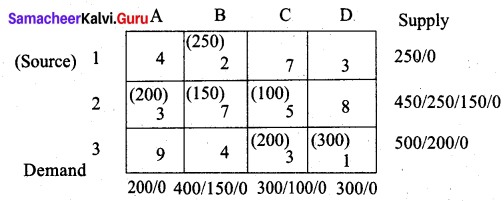
Transportation cost is = (250 × 2) + (200 × 3) + (150 × 7) + (100 × 5) + (200 × 3) + (300 × 1)
= 500 + 600+ 1050 + 500 + 600 + 300
= Rs. 3550
![]()
(iii) Vogel Approximation Method (VAM)
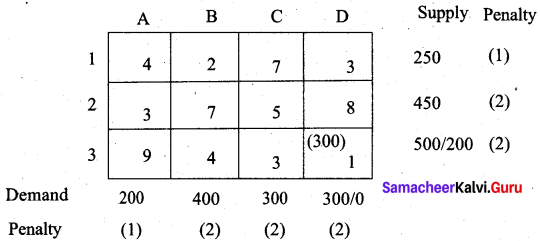
There are five penalties which have the maximum value 2. The cell with the least cost is row 3 and hence select cell (3, D) for allocation.
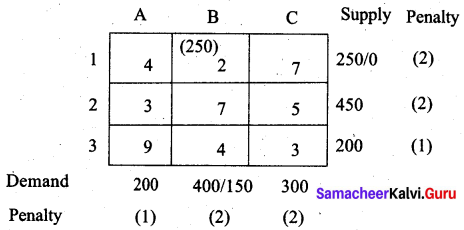
There are four penalties which have maximum value 2. Select cell (1, B) which has the least cost for allocation.
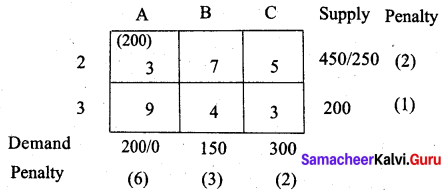
The largest penalty is 6. Allot units to cell (2, A)
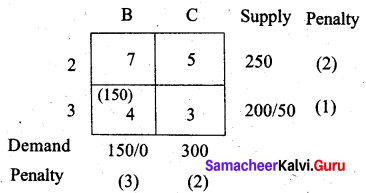
The largest penalty is 3. Allot units to cell (3, B)
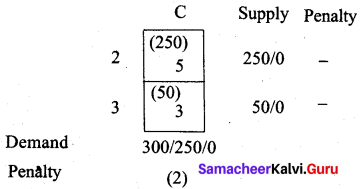
We first allot 50 units to cell (3, C) which has less cost. Then the balance units we allot to cell (2, C). We get the final allocation table as follows.
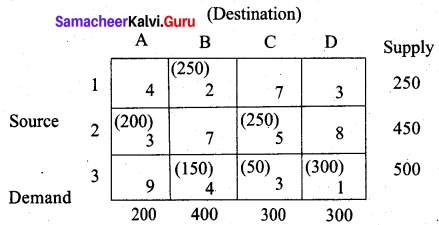
Transportation cost is = (250 × 2) + (200 × 3) + (250 × 5) + (150 × 4) + (50 × 3) + (300 × 1)
= 500 + 600 + 1250 + 600 + 150 + 300
= Rs. 3400