Students can Download Physics Chapter 8 Heat and Thermodynamics Questions and Answers, Notes Pdf, Samacheer Kalvi 11th Physics Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Physics Solutions Chapter 8 Heat and Thermodynamics
Samacheer Kalvi 11th Physics Heat and Thermodynamics Textual Evaluation Solved
Samacheer Kalvi 11th Physics Heat and Thermodynamics Multiple Choice Questions
Question 1.
In hot summer after a bath, the body’s …….
(a) internal energy decreases
(b) internal energy increases
(c) heat decreases
(d) no change in internal energy and heat
Answer:
(a) internal energy decreases
Question 2.
The graph between volume and temperature in Charles’ law is …….
(a) an ellipse
(b) a circle
(c) a straight line
(d) a parabola
Answer:
(c) a straight line
![]()
Question 3.
When a cycle tyre suddenly bursts, the air inside the tyre expands. This process is …..
(a) isothermal
(b) adiabatic
(c) isobaric
(d) isochoric
Answer:
(b) adiabatic
Question 4.
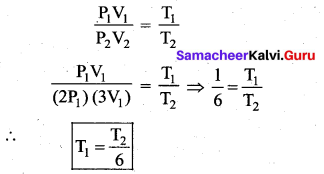
An ideal gas passes from one equilibrium state (P1, V1, T1, N) to another equilibrium state
(2P1, 3V1, T2, N). Then ………
![]()
Answer:
(b) \(\mathrm{T}_{1}=\frac{\mathrm{T}_{2}}{6}\)
Solution:
From ideal gas equation, PV = NkT
One equilibrium state (P1, V1, T1, N)
Another equilibrium state (P2, V2, T2, N)
P2 = 2P1, and V2 = 3V1
Question 5.
When a uniform rod is heated, which of the following quantity of the rod will increase
(a) mass
(b) weight
(c) center of mass
(d) moment of inertia
Answer:
(d) moment of inertia
Question 6.
When food is cooked in a vessel by keeping the lid closed, after some time the steam pushes the lid outward. By considering the steam as a thermodynamic system, then in the cooking process …….
(a) Q > 0, W > 0
(b) Q < 0, W > 0
(c) Q > 0, W < 0
(d) Q < 0, W < 0 Answer: (a) Q > 0, W > 0
Question 7.
When you exercise in the morning, by considering your body as thermodynamic system, which of the following is true?
(a) ∆U > 0, W > 0
(b) ∆U < 0, W > 0
(c) ∆U < 0, W < 0
(d) ∆U = 0, W > 0
Answer:
(b) ∆U < 0, W > 0
Question 8.
A hot cup of coffee is kept on the table. After some time it attains a thermal equilibrium with the surroundings. By considering the air molecules in the room as a thermodynamic system, which of the following is true?
(a) ∆U > 0, Q = 0
(b) ∆U > 0, W < 0 (c) ∆U > 0, Q > 0
(d) ∆U = 0, Q > 0
Answer:
(c) ∆U > 0, Q > 0
Question 9.
An ideal gas is taken from (Pi, Vi) to (Pf, Vf) in three different ways. Identify the process in which the work done on the gas the most.
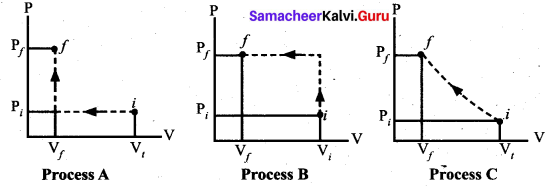
(a) Process A
(b) Process B
(c) Process C
(d) Equal work is done in Process A, B & C
Answer:
(b) Process B
Question 10.
The V-T diagram of an ideal gas which goes through a reversible cycle A ➝ B ➝ C ➝ D is shown below. (Processes D ➝ A and B ➝ C are adiabatic)
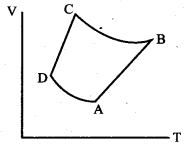
The corresponding PV diagram for the process is (all figures are schematic)
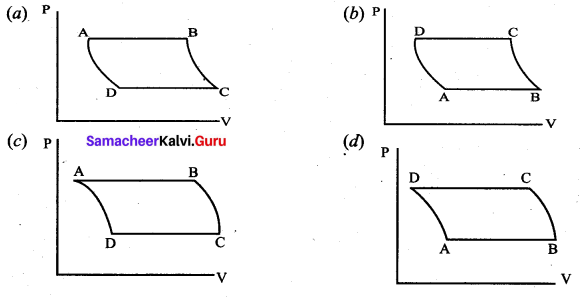
Answer:
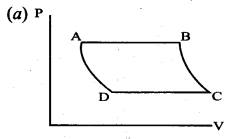
Question 11.
A distant star emits radiation with maximum intensity at 350 nm. The temperature of the star is
(a) 8280 K
(b) 5000 K
(c) 7260 K
(d) 9044 K
Answer:
(a) 8280 K
Solution:
According to Wien’s displacement law,
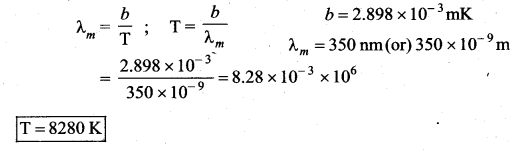
Question 12.
Identify the state variables given here?
(a) Q, T, W
(b) P, T, U
(c) Q, W
(d) P, T, Q
Answer:
(b) P, T, U
![]()
Question 13.
In an isochoric process, we have ……
(a) W = 0
(b) Q = 0
(c) ∆U = 0
(d) ∆T = 0
Answer:
(a) W = 0
Question 14.
The efficiency of a heat engine working between the freezing point and boiling point of water is ….. [NEET 2018]
(a) 6.25%
(b) 20%
(c) 26.8%
(d) 12.5%
Answer:
(c) 26.8%
Solution:
The freezing point of water = 0°C = 273 K
Boiling point of water = 100°C = 373 K
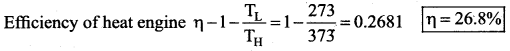
Question 15.
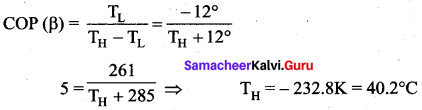
An ideal refrigerator has a freezer at temperature -12°C. The coefficient of performance of the engine is 5. The temperature of the air (to which the heat ejected) is …..
(a) 50°C
(b) 45.2°C
(c) 40.2°C
(d) 37.5°C
Answer:
(c) 40.2°C
Solution:
Samacheer Kalvi 11th Physics Heat and Thermodynamics Short Answer Questions
Question 1.
‘An object contains more heat’- is it a right statement? If not why?
Answer:
When heated, an object receives heat from the agency. Now object has more internal energy than before. Heat is the energy in transit and which flows from an object at higher temperature to an object lower temperature. Heat is not a quantity. So the statement I would prefer “an object contains more thermal energy”.
Question 2.
Obtain an ideal gas law from Boyle’s and Charles’ law.
Answer:
Boyle’s law: When the gas is kept at constant temperature, the pressure of the gas is inversely proportional to the volume \(\mathrm{P} \propto \frac{1}{\mathrm{V}}\)
Charles’ law: When the gas is kept at constant pressure, the volume of the gas is directly proportional to absolute temperature V ∝ T.
![]()
Question 3.
Define one mole.
Answer:
One mole of any substance is the amount of that substance which contains Avogadro number (NA) of particles (such as atoms or molecules).
Question 4.
Define specific heat capacity and give its unit.
Answer:
Specific heat capacity of a substance is defined as the amount of heat energy required into raise the temperature of 1 kg of a substance by 1 Kelvin or 1°C
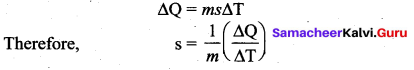
The SI unit for specific heat capacity is J kg-1 K-1
Question 5.
Define molar specific heat capacity.
Answer:
Molar specific heat capacity is defined as heat energy required to increase the temperature of one mole of substance by IK or 1°C. 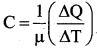
Question 6.
What is a thermal expansion?
Answer:
Thermal expansion is the tendency of matter to change in shape, area, and volume due to a change in temperature.
Question 7.
Give the expressions for linear, area and volume thermal expansions.
Answer:
Linear Expansion: In solids, for a small change in temperature ∆T, the fractional change in length \(\left(\frac{\Delta \mathrm{L}}{\mathrm{L}_{0}}\right)\) is directly proportional to ∆T.
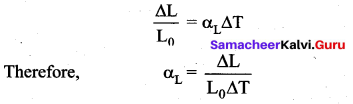
Area Expansion: For a small change in temperature ∆T the fractional change in area \(\left(\frac{\Delta \mathrm{A}}{\mathrm{A}_{0}}\right)\) of a substance is directly proportional to ∆T and it can be written as
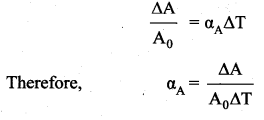
Volume Expansion: For a small change in temperature ∆T the fractional change in volume \(\left(\frac{\Delta \mathrm{V}}{\mathrm{V}_{0}}\right)\) of a substance is directly proportional to ∆T.
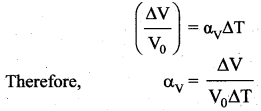
Question 8.
Define latent heat capacity. Give its unit.
Answer:
Latent heat capacity of a substance is defined as the amount of heat energy required to change the state of a unit mass of the material.
Question 9.
State Stefan-Boltzmann law.
Answer:
Stefan Boltzmann law states that, the total amount of heat radiated per second per unit area of a black body is directly proportional to the fourth power of its absolute temperature.
![]()
Question 10.
What is Wien’s law?
Answer:
Wien’s law states that, the wavelength of maximum intensity of emission of a black body radiation is inversely proportional to the absolute temperature of the black body.
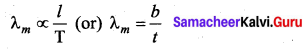
Question 11.
Define thermal conductivity. Give its unit.
Answer:
The quantity of heat transferred through a unit length of a material in a direction normal to Unit surface area due to a unit temperature difference under steady state conditions is known as thermal conductivity of a material.
![]()
Question 12.
What is a black body?
Answer:
A black body is one which neither reflects nor transmits but absorbs whole of the heat radiation incident on it.
The absorptive power of a perfect black body is unity.
Question 13.
What is a thermodynamic system? Give examples.
Answer:
Thermodynamic system: A thermodynamic system is a finite part of the universe. It is a collection of large number of particles (atoms and molecules) specified by certain parameters called pressure (P), Volume (V) and Temperature (T). The remaining part of the universe is called surrounding. Both are separated by a boundary.
Examples: A thermodynamic system can be liquid, solid, gas and radiation.
Question 14.
What are the different types of thermodynamic systems?
Answer:
- Open system can exchange both matter and energy with the environment.
- Closed system exchange energy but not matter with the environment.
- Isolated system can exchange neither energy nor matter with the environment.
Question 15.
What is meant by ‘thermal equilibrium’?
Answer:
Two systems are said to be in thermal equilibrium with each other if they are at the same temperature, which will not change with time.
Question 16.
What is mean by state variable? Give example.
Answer:
In thermodynamics, the state of a thermodynamic system is represented by a set of variables called thermodynamic variables.
Examples: Pressure, temperature, volume and internal energy etc.
Question 17.
What are intensive and extensive variables? Give examples.
Answer:
Extensive variable depends on the size or mass of the system.
Example : Volume, total mass, entropy, internal energy, heat capacity etc.
Intensive variables do not depend on the size or mass of the system.
Example: Temperature, pressure, specific heat capacity, density etc.
![]()
Question 18.
What is an equation of state? Give an example.
Answer:
Equation of state: The equation which connects the state variables in a specific manner is called equation of state. An ideal gas obeys the equation PV = NkT at thermodynamic equilibrium.
For example, if we push the piston of a gas container, the volume of the gas will decrease but pressure will increase or if heat is supplied to the gas, its temperature will increase, pressure and volume of the gas may also increase.
Question 19.
State Zeroth law of thermodynamics.
Answer:
The zeroth law of thermodynamics states that if two systems, A and B, are in thermal equilibrium with a third system C, then A and B are in thermal equilibrium with each other.
Question 20.
Define the internal energy of the system.
Answer:
The internal energy of a thermodynamic system is the sum of kinetic and potential energies of all the molecules of the system with respect to the center of mass of the system.
Question 21.
Are internal energy and heat energy the same? Explain.
Answer:
Internal energy and thermal energy do not mean the same thing, but they are related. Internal energy is the energy stored in a body. It increases when the temperature of the body rises, or when the body changes from solid to liquid or from liquid to gas.
“Heat is the energy transferred from one body to another as a result of a temperature difference.”
Question 22.
Define one calorie.
Answer:
One calorie is defined as the amount of heat energy needed to raise the temperature of one gram of water by one degree Celsius at a pressure of one atmosphere.
Question 23.
Did joule converted mechanical energy to heat energy? Explain.
Answer:
Joule essentially converted mechanical energy to internal energy. In his experiment potential energy is converted to rotational kinetic energy of paddle wheel and this rotational kinetic energy is converted to internal energy of water.
Question 24.
State the first law of thermodynamics.
Answer:
This law states that ‘Change in internal energy (∆U) of the system is equal to heat supplied to the system (Q) minus the work done by the system (W) on the surroundings’.
Question 25.
Can we measure the temperature of the object by touching it?
Answer:
No, we can’t measure the temperature of the object touching it. Because the temperature is the degree of hotness or coolness of a body. Only we can sense the hotness or coolness of the object.
![]()
Question 26.
Give the sign convention for Q and W.
Answer:
System gains heat Q is positive
System loses heat Q is negative
Work done on the system W is negative
Work done by the system W is positive
Question 27.
Define the quasi-static process.
Answer:
A quasi-static process is an infinitely slow process in which the system changes its variables (P, V, T) so slowly such that it remains in thermal, mechanical and chemical equilibrium with its surroundings throughout.
Question 28.
Give the expression for work done by the gas.
Answer:
When a gas expands against pressure, it does work on the surroundings. The work done in expansion for volume V1 to V2 is given by
![]()
If the pressure remains constant during expansion,
Then W = P(V2 – V1) = P∆V
If the volume remains constant, then W = 0.
If there is no external pressure, then no work is done. For example, when a gas expands freely in vaccum, no work is done by it.
Question 29.
What is PV diagram?
Answer:
PV diagram is a graph between pressure P and volume V of the system. The P-V diagram is used to calculate the amount of work done by the gas during expansion or on the gas during compression.
Question 30.
Explain why the specific heat capacity at constant pressure is greater than the specific heat capacity at constant volume.
Answer:
It implies that to increase the temperature of the gas at constant volume requires less heat than increasing the temperature of the gas at constant pressure. In other words s is always greater than sv.
Question 31.
Give the equation of state for an isothermal process.
Answer:
It is a process in which the temperature remains constant but the pressure and volume of a thermodynamic system will change. The ideal gas equation is PV = µRT
Question 32.
Give an expression for work done in an isothermal process.
Answer:

Question 33.
Express the change in internal energy in terms of molar specific heat capacity.
Answer:
When the gas is heated at constant volume the temperature increases by dT. As no work is done by the gas, the heat that flows into the system will increase only the internal energy. Let the change in internal energy be dU. dU = µωdT
Question 34.
Apply first law for
(a) an isothermal
(b) adiabatic
(c) isobaric processes.
Answer:
(a) For an isothermal process since temperature is constant, the internal energy is also constant. This implies that dU or ∆U = 0.
For an isothermal process, the first law of thermodynamics can be written as follows,
Q = W
(b) This is a process in which no heat flows into or out of the system (Q = 0). But the gas can expand by spending its internal energy or gas can be compressed through some external work. So the pressure, volume and temperature of the system may change in an adiabatic process. For an adiabatic process, the first law becomes ∆U = W.
(c) The first law of thermodynamics for isobaric process is given by
∆U = Q – P∆Y
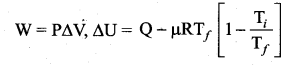
Question 35.
Give the equation of state for an adiabatic process.
Answer:
The equation of state for an adiabatic process is given by
![]()
Here γ is called adibatic exponent
(γ = Cp/Cγ) which depends on the nature of the gas
Question 36.
Give an equation state for an isochoric process.
Answer:
The equation of state for an isochoric process is given by
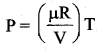
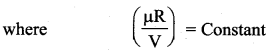
We can infer that the pressure is directly proportional to temperature. This implies that the P-T graph for an isochoric process is a straight line passing through origin.
Question 37.
If the piston of a container is pushed fast inward. Will the ideal gas equation be valid in the intermediate stage? If not, why?
Answer:
When the piston is compressed so quickly that there is no time to exchange heat to the surrounding, the temperature of the gas increases rapidly. In this intermediate stage the ideal gas equation be not valid. Because this equation can be relates the pressure, volume and temperature of thermodynamic system at equilibrium.
Question 38.
Draw the PV diagram for:
(a) Isothermal process
(b) Adiabatic process
(c) isobaric process
(d) Isochoric process
(a) Isothermal process:
Answer:
(a) Isothermal process
(b) Adiabatic process:
(c) isobaric process:
(d) Isochoric process:
Question 39.
What is a cyclic process?
Answer:
This is a thermodynamic process in which the thermodynamic system returns to its initial state after undergoing a series of changes. Since the system comes back to the initial state, the change in the internal energy is zero. In cyclic process, heat can flow in to system and heat flow out of the system. From the first law of thermodynamics, the net heat transferred to the system is equal to work done by the gas.
Qnet = Qin – Qout = W (for a Cyclic Process)
Question 40.
What is meant by a reversible and irreversible processes?
Answer:
Reversible processes: A thermodynamic process can be considered reversible only if it possible to retrace the path in the opposite direction in such a way that the system and surroundings pass through the same states as in the initial, direct process.
Irreversible processes: All natural processes are irreversible. Irreversible process cannot be plotted in a PV diagram, because these processes cannot have unique values of pressure, temperature at every stage of the process.
![]()
Question 41.
State Clausius form of the second law of thermodynamics.
Answer:
“Heat always flows from hotter object to colder object spontaneously”. This is known as the Clausius form of second law of thermodynamics.
Question 42.
State Kelvin-Planck statement of second law of thermodynamics.
Answer:
Kelvin-Planck statement: It is impossible to construct a heat engine that operates in a cycle, whose sole effect is to convert the heat completely into work. This implies that no heat engine in the universe can have 100% efficiency.
Question 43.
Define heat engine.
Answer:
Heat engine is a device which takes heat as input and converts this heat in to work by undergoing a cyclic process.
Question 44.
What are processes involves in a Carnot engine?
Answer:
There are four processes involves in a carnot engine:
- source
- sink
- insulating stand
- working substance
Question 45.
Can the given heat energy be completely converted to work in a cyclic process? If not, when can the heat can completely converted to work?
Answer:
According to first law of thermodynamics work can be completely converted into heat. Since the system comes back to the initial stage, the change in the internal energy is zero. In cyclic process, heat can flow in to system and heat flow out of the system. The net heat transferred to the system is equal to work done by the gas.
Qnet = Qin = Qout = W (for 3 Cyclic Process)
Question 46.
State the second law of thermodynamics in terms of entropy.
Answer:
“For all the processes that occur in nature (irreversible process), the entropy always increases. For reversible process entropy will not change”. Entropy determines the direction in which natural process should occur.
Question 47.
Why does heat flow from a hot object to a cold object?
Answer:
Because entropy increases when heat flows from hot object to cold object. If heat were to flow from a cold to a hot object, entropy will decrease leading to violation of second law thermodynamics.
Question 48.
Define the coefficient of performance.
Answer:
It is defined as the ratio of heat extracted from the cold body (sink) to the external work done by the compressor W.
Samacheer Kalvi 11th Physics Heat and Thermodynamics Long Answer Questions
Question 1.
Explain the meaning of heat and work with suitable examples.
Answer:
Meaning of heat: When an object at higher temperature is placed in contact with another object at lower temperature, there will be a spontaneous flow of energy from the object at higher temperature to the one at lower temperature. This energy is called heat. This process of energy transfer from higher temperature object to lower temperature object is called heating. Due to flow of heat sometimes the temperature of the body will increase or sometimes it may not increase.

Meaning of work: When you rub your hands against each other the temperature of the hands increases. You have done some work on your hands by rubbing. The temperature of the hands increases due to this work. Now if you place your hands on the cheek, the temperature of the cheek increases. This is because the hands are at higher temperature than the cheek. In the above example, the temperature of hands is increased due to work and temperature of the cheek is increased due to heat transfer from the hands to the chin. It is shown in the Figure. By doing work on the system, the temperature in the system will increase and sometimes may not. Like heat, work is also not a quantity and through the work energy is transferred to the system. So we cannot use the word ‘the object contains more work’ or ‘less work’.
Either the system can transfer energy to the surrounding by doing work on surrounding or the surrounding may transfer energy to the system by doing work on the system. For the transfer of energy from one body to another body through the process of work, they need not be at different temperatures.
Question 2.
Discuss the ideal gas laws.
Answer:
Boyle’s law: For a given gas at low pressure (density) kept in a container of volume V, experiments revealed the following information.
When the gas is kept at constant temperature, the pressure of the gas is inversely proportional to the volume \(\mathrm{P} \propto \frac{1}{\mathrm{V}}\)
Charles’ law: When the gas is kept at constant pressure, the volume of the gas is directly proportional to absolute temperature V ∝ T.
By combining these two equations we have
PV = CT. Here C is a positive constant.
We can infer that C is proportional to the number of particles in the gas container by considering the following argument. If we take two containers of same type of gas with same volume V, same pressure P and same temperature T, then the gas in each container obeys the above equation. PV = CT. If the two containers of gas is considered as a single system, then the pressure and temperature of this combined system will be same but volume will be twice and number of particles will also be double.
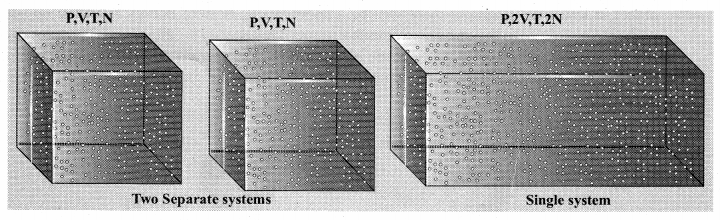
For this combined system, V becomes 2V, so C should also double to match with the ideal gas equation \(\frac{P(2 V)}{T}=2 C\). It implies that C must depend on the number of particles in the gas and also should have the dimension of \(\left[\frac{\mathrm{pv}}{\mathrm{T}}\right]=\mathrm{JK}^{-1}\). So we can write the constant C as k times the number of particles N.
Here k is the Boltzmann constant (1.381 × 10-23 JK-1) and it is found to be a universal constant. So the ideal gas law can be stated as follows
PV = NkT …(1)
The equation (1) can also be expressed in terms of mole.
Suppose if a gas contains p mole of particles then the total number of particles can be written as
N = µNA …… (2)
where NA is Avogadro number (6.023 × 1023 mol-1)
Substituting for N from equation (2), the equation (1) becomes PV = µNAkT. Here NAk = R called universal gas constant and its value is 8.314 J /mol. K
So the ideal gas law can be written for µ mole of gas as
PV = μRT …(3)
This is called the equation of state for an ideal gas. It relates the pressure, volume and temperature of thermodynamic system at equilibrium.
![]()
Question 3.
Explain in detail the thermal expansion.
Answer:
Thermal expansion is the tendency of matter to change in shape, area, and volume due to a change in temperature.
All three states of matter (solid, liquid and gas) expand when heated. When a solid is heated, its atoms vibrate with higher amplitude about their fixed points. The relative change in the size of solids is small. Railway tracks are. given small gaps so that in the summer, the tracks expand and do not buckle. Railroad tracks and bridges have expansion joints to allow them to expand and contract freely with temperature changes.

Liquids, have less intermolecular forces than solids and hence they expand more than solids. This is the principle behind the mercury thermometers.
In the case of gas molecules, the intermolecular forces are almost negligible and hence they expand much more than solids. For example in hot air balloons when gas particles get heated, they expand and take up more space.
The increase in dimension of a body due to the increase in its temperature is called thermal expansion.
The expansion in length is called linear expansion. Similarly the expansion in area is termed as area expansion and the expansion in volume is tenned as volume expansion.
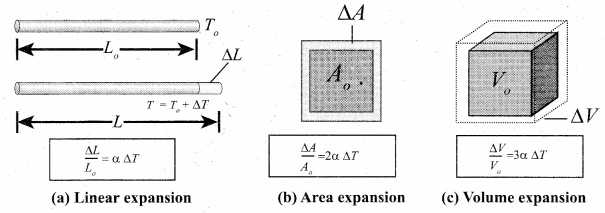
Linear Expansion: In solids, for a small change in temperature ∆T, the fractional change in length \(\left(\frac{\Delta \mathrm{L}}{\mathrm{L}_{0}}\right)\) is directly proportional to ∆T
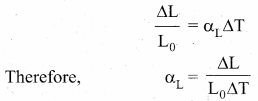
Where, αL = coefficient of linear expansion,
∆L = Change in length,
L = Original length,
∆T = Change in temperature.
Area Expansion: For a small change in temperature ∆T the fractional change in area \(\left(\frac{\Delta \mathrm{A}}{\mathrm{A}_{0}}\right)\) of a substance is directly proportional to ∆T and it can be written as
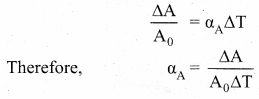
Where, αA = coefficient of area expansion.
∆A = Change in area,
A = Original area,
∆T = Change in temperature.
Volume Expansion: For a small change in temperature AT the fractional change in volume \(\left(\frac{\Delta \mathrm{V}}{\mathrm{V}_{0}}\right)\) of a substance is directly proportional to ∆T.
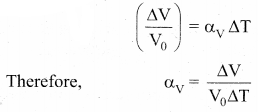
Where, αv = coefficient of volume expansion,
∆V = Change in volume,
V = Original volume,
∆T = Change in temperature,
Unit of coefficient of linear, area and volumetric expansion of solids is °C-1 or K-1
Question 4.
Describe the anomalous expansion of water: How is it helpful in our lives?
Answer:
Anomalous expansion of water : Liquids expand on heating and contract on cooling at moderate temperatures. But water exhibits an anomalous behavior. It contracts on heating between 0°C and 4°C. The volume of the given amount of water decreases as it is cooled from room temperature, until it reach 4°C. Below 4°C the volume increases and so the density decreases. This means that the water has a maximum density at 4°C. This behavior of water is called anomalous expansion of water.
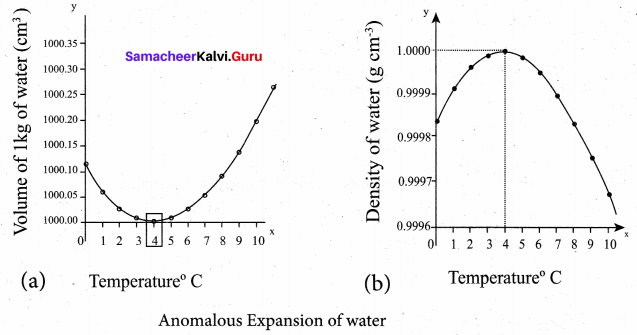
In cold countries during the winter season, the surface of the lakes will be at lower temperature than the bottom as shown in the Figure. Since the solid water (ice) has lower density than its liquid form, below 4°C, the frozen water will be on the top surface above the liquid water (ice floats). This is due to the anomalous expansion of water. As the water in lakes and ponds freeze only at the top the species living in the lakes will be safe at the bottom.
Question 5.
Explain Calorimetry and derive an expression for final temperature when two thermodynamic systems are mixed.
Answer:
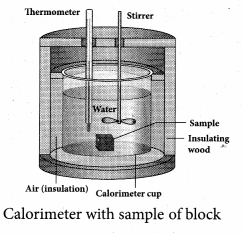
Calorimetry: Calorimetry means the measurement of the amount of heat released or absorbed by thermodynamic system during the heating process. When a body at higher temperature is brought in contact with another body at lower temperature, the heat lost by the hot body is equal to the heat gained by the cold body. No heat is allowed to escape to the surroundings. It can be Anomalous expansion of water in lakes mathematically expressed as

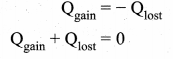
Heat gained or lost is measured with a calorimeter. Usually the calorimeter is an insulated container of water. A sample is heated at high temperature (T1) and immersed into water at room temperature (T2) in the calorimeter. After some time both sample and water reach a final equilibrium temperature Tf. Since the calorimeter is insulated, heat given by the water.
Qgain = – Qlost
Note the sign convention. The heat lost is denoted by negative sign and heat gained is denoted as positive.
From the definition of specific heat capacity
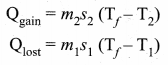
Here S1 and s2 specific heat capacity of hot sample and water respectively.
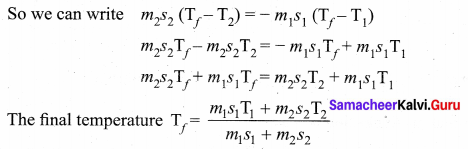
![]()
Question 6.
Discuss various modes of heat transfer.
Answer:
There are three modes of heat transfer: Conduction, Convection and Radiation.

Conduction: Conduction is the process of direct transfer of heat through matter due to temperature difference. When two objects are in direct contact with one another, heat will be transferred from the hotter object to the colder one. The objects which allow heat to travel easily through them are called conductors.
Convection: Convection is the process in which heat transfer is by actual movement of molecules in fluids such as liquids and gases. In convection, molecules move freely from one place to another.
Boiling water in a cooking pot is an example of convection. Water at the bottom of the pot receives more heat. Due to heating, the water expands and the density of water decreases at the bottom. Due to this decrease in density, molecules rise to the top. At the same time the molecules at the top receive less heat and become denser and come to the bottom of the pot. This process goes on continuously. The back and forth movement of molecules is called convection current.
To keep the room warm, we use room heater. The air molecules near the heater will heat up and expand. As they expand, the density of air molecules will decrease and rise up while the higher density cold air will come down. This circulation of air molecules is called convection current.
Radiation: When we keep our hands near the hot stove we feel the heat even though our hands are not touching the hot stove. Here heat transferred from the hot stove to our hands is in the form of radiation. We receive energy from the sun in the form of radiations. These radiations travel through vaccum and reach the Earth. It is the peculiar character of radiation which requires no medium to transfer energy from one object to another. The conduction or convection requires medium to transfer the heat.
Radiation is a form of energy transfer from one body to another by electromagnetic waves.
Example:
1. Solar energy from the Sun.
2. Radiation from hot stove.
Question 7.
Explain in detail Newton’s law of cooling.
Answer:
Newton’s law of cooling: Newton’s law of cooling states that the rate of loss of heat of a body is directly proportional to the difference in the temperature between that body and its surroundings.
![]()
The negative sign indicates that the quantity of heat lost by liquid goes on decreasing with time. Where,
T = Temperature of the object
Ts = Temperature of the surrounding
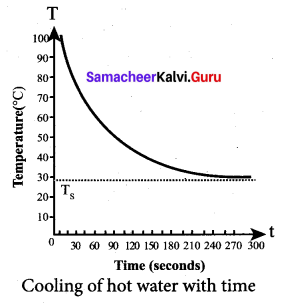
From the graph in figure it is clear that the rate of cooling is high initially and decreases with falling temperature.
Let us consider an object of mass m and specific heat capacity s at temperature T. Let Ts be the temperature of the surroundings. If the temperature falls by a small amount dT in time dt, then the amount of heat lost is,
![]()
Dividing both sides of equation (2) by dt
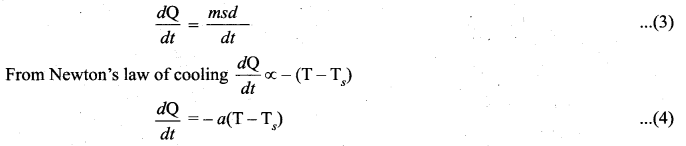
Where a is some positive constant. From equation (3) and (4)
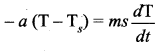

Integrating equation (5) on both sides,
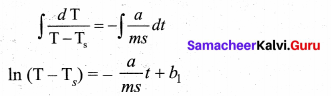
Where b1, is the constant of integration. Taking exponential both sides, we get

Question 8.
Explain Wien’s law and why our eyes are sensitive only to visible rays?
Answer:
Wien’s law and Vision:
The Sun is approximately taken as a black body. Since any object above 0 K will emit radiation, Sun also emits radiation. Its surface temperature is about 5700 K. By substituting this value in the equation of Wien’s law.
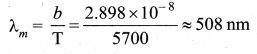
It is the wavelength at which maximum intensity is 508 nm. Since the Sun’s temperature is around 5700 K, the spectrum of radiations emitted by Sun lie between 400 nm to 700 nm which is the visible part, of the spectrum. It is shown in Figure.
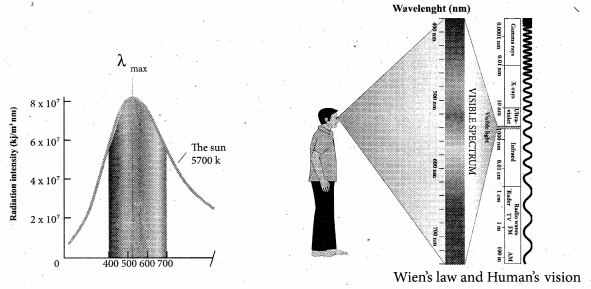
The humans evolved under the Sun by receiving its radiations. The human eye is sensitive only in the visible not in infrared or X-ray ranges in the spectrum.
Suppose if humans had evolved in a planet near the star Sirius (9940K), then they would have had the ability to see the Ultraviolet rays!
Question 9.
Discuss the:
(a) thermal equilibrium
(b) mechanical equilibrium
(c) chemical equilibrium
(d) thermodynamic equilibrium.
Answer:
(a) Thermal equilibrium: When a hot cup of coffee is kept in the room, heat flows from coffee to the surrounding air. After sometime the coffee reaches the same temperature as the surrounding air and there will be no heat flow from coffee to air or air to coffee. It implies that the coffee and surrounding air are in thermal equilibrium with each other. Two systems are said to be in thermal equilibrium with each other if they arc at the same temperature, which Mechanical equilibrium will not change with time.
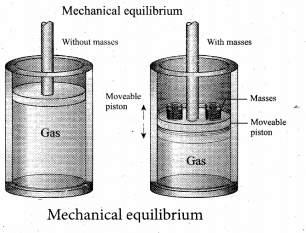
(b) Mechanical equilibrium: Consider a gas container with piston. When some mass is placed on the piston, it will move downward due to downward gravitational force and after certain humps and jumps the piston will come to rest at a new position. When the downward gravitational force given by the piston is balanced by the upward force exerted by the gas, the system is said to be in mechanical equilibrium. A system is said to be in mechanical equilibrium if no unbalanced force acts on the thermo dynamic system or on the surrounding by thermodynamic system.
(c) Chemical equilibrium: If there is no net chemical reaction between two thermodynamic systems in contact with each other then it is said to be in chemical equilibrium.
(d) Thermodynamic equilibrium: If two systems are set to be in thermodynamic equilibrium, then the systems are at thermal, mechanical and chemical equilibrium with each other. In a state of thermodynamic equilibrium the macroscopic variables such as pressure, volume and temperature will have fixed values and do not change with time.
Question 10.
Explain Joule’s Experiment of the mechanical equivalent of heat.
Answer:
Joule’s mechanical equivalent of heat: The temperature of an object can be increased by heating it or by doing some work on it.
In the eighteenth century, James Prescott Joule showed that mechanical energy can be converted into internal energy and vice versa.
In his experiment, two masses were attached with a rope and a paddle wheel as shown in Figure. When these masses fall through a distance h due to gravity, both the masses lose potential energy equal to 2 mgh. When the masses fall, the paddle wheel turns. Due to the turning of wheel inside water, frictional force comes in between the water and the paddle wheel.
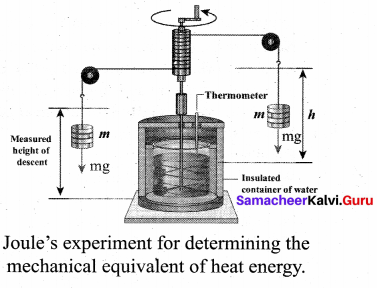
This causes a rise in temperature of the water. This implies that gravitational potential energy is converted to internal energy of water. The temperature of water increases due to the work done by the masses. In fact, Joule was able to show that the mechanical work has the same effect as giving heat. He found that to raise 1 g of an object by 1°C, 4.186 J of energy is required. In earlier days the heat was measured in calorie.
1 cal = 4.186 J
This is called Joule’s mechanical equivalent of heat.
![]()
Question 11.
Derive the expression for the work done in a volume change in a thermodynamic system.
Answer:
Work done in volume changes: Consider a gas contained in the cylinder fitted with a movable piston. Suppose the gas is expanded quasi-statically by pushing the piston by a small distance dx. Since the expansion occurs quasi-statically the pressure, temperature and internal energy will have unique values at every instant.
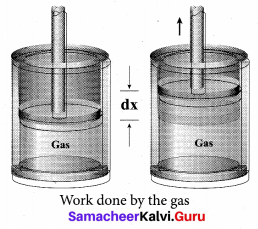
The small work done by the gas on the piston
dW = Fdx …(1)
The force exerted by the gas on the piston F = PA.
Here A is area of the piston and P is pressure exerted by the gas on the piston.
Equation (1) can be rewritten as Work done by the gas
dW = PA dx …(2)
But Adx = dV= change in volume during this expansion process.
So the small work done by the gas during the expansion is given by
dW = PdV ….(3)
dV is positive since the volume is increased. Here, dW is positive.
In general the work done by the gas by increasing the volume from Vi to Vf is given by
![]()
Suppose if the work is done on the system, then Vi > Vf. Then, W is negative.
Note here the pressure P is inside the integral in equation (4). It implies that while the system is doing work, the pressure need not be constant. To evaluate the integration we need to first express the pressure as a function of volume and temperature using the equation of state.
Question 12.
Derive Mayer’s relation for an ideal gas.
Answer:
Mayer’s relation: Consider p mole of an ideal gas in a container with volume V, pressure P and temperature T.
When the gas is heated at constant volume the temperature increases by dT. As no work is done by the gas, the heat that flows into the system will increase only the internal energy. Let the change in internal energy be dU.
If Cv is the molar specific heat capacity at constant volume, from equation.

Suppose the gas is heated at constant pressure so that the temperature increases by dT. If ‘Q’ is the heat supplied in this process and ‘dV’ the change in volume of the gas.
Q = µCPdT …(3)
If W is the workdone by the gas in this process, then
W = P dV …(4)
But from the first law of thermodynamics,
Q = dU + W …. (5)
Substituting equations (2), (3) and (4) in (5), we get,
![]()
For mole of ideal gas, the equation of state is given by
![]()
Since the pressure is constant, dP = 0
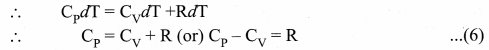
This relation is called Mayer’s relation It implies that the molar specific heat capacity of an ideal gas at constant pressure is greater than molar specific heat capacity at constant volume. The relation shows that specific heat at constant pressure (sp) is always greater than specific heat at constant volume (sv).
Question 13.
Explain in detail the isothermal process.
Answer:
Isothermal process: It is a process in which the temperature remains constant but the pressure and volume of a thermodynamic system will change. The ideal gas equation is
PV = µRT
Here, T is constant for this process So the equation of state for isothermal process is given by
PV= Constant …(1)
This implies that if the gas goes from one equilibrium state (P1, V1) to another equilibrium state (P2, V2) the following relation holds for this process
P1V1 = P2V2 …(2)
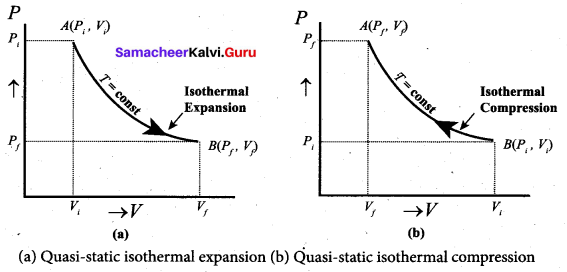
Since PV = constant, P is inversely proportional to \(v\left(P \propto \frac{1}{V}\right)\). This implies that PV graph is a hyperbola. The pressure-volume graph for constant temperature is also called isotherm. We know that for an ideal gas the internal energy is a function of temperature only. For an isothermal process since temperature is constant, the internal energy is also constant. This implies that dU or ∆U = 0.
For an isothermal process, the first law of thermodynamics can be written as,
Q = W …(3)
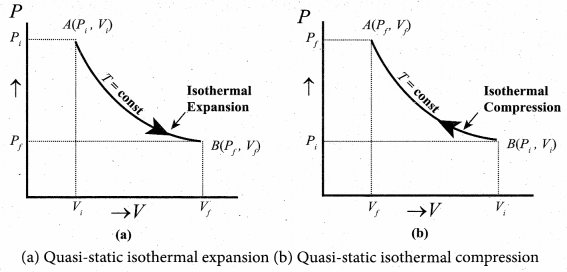
From equation (3), we infer that the heat supplied to a gas is used to do only external work. It is a common misconception that when there is flow of heat to the system, the temperature will increase. For isothermal process this is not true. The isothermal compression takes place when the piston of the cylinder is pushed. This will increase the internal energy which will flow out of the system through thermal contact.
Question 14.
Derive the work done in an isothermal process.
Answer:
Work done in an isothermal process: Consider an ideal gas which is allowed to expand quasi-statically at constant temperature from initial state (Pi, Vi) to the final state (Pf, Vf). We can calculate the work done by the gas during this process. The work done by the gas,
![]()
As the process occurs quasi-statically, at every stage the gas is at equilibrium with the surroundings. Since it is in equilibrium at every stage the ideal gas law is valid. Writing pressure in terms of volume and temperature,

Substituting equation (2) in (1) we get

In equation (3), we take uRT out of the integral, since it is constant throughout the isothermal process.
By performing the integration in equation (3), we get

As a result the work done on the gas in an isothermal compression is negative.
In the PV diagram the work done during the isothermal expansion is equal to the area under the graph.
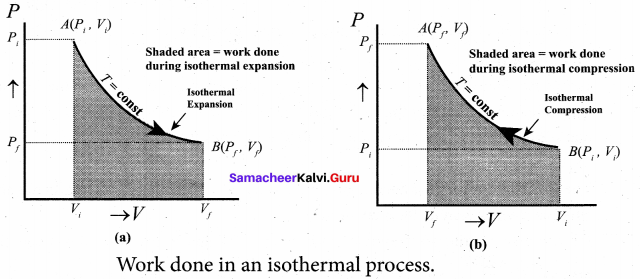
Similarly for an isothermal compression, the area under the PV graph is equal to the work done on the gas which turns out to be the area with a negative sign.
Question 15.
Explain in detail an adiabatic process.
Answer:
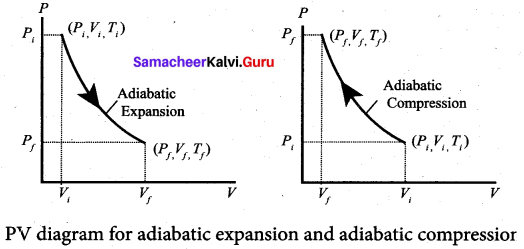
Adiabatic process: This is a process in which no heat flows into or out of the system (Q = 0). But the gas can expand by spending its internal energy or gas can be compressed through some external work. So the pressure, volume and temperature of the system may change in an adiabatic process.
For an adiabatic process, the first law becomes ∆U = W.
This implies that the work is done by the gas at the expense of internal energy or work is done on the system which increases its internal energy.
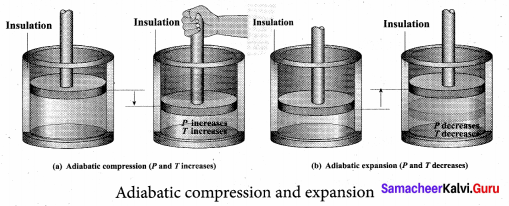
The adiabatic process can be achieved by the following methods:
(i) Thermally insulating the system from surroundings so that no heat flows into or out of the system; for example, when thermally insulated cylinder of gas is compressed (adiabatic compression) or expanded (adiabatic expansion) as shown in the Figure.
(ii) If the process occurs so quickly that there is no time to exchange heat with surroundings even though there is no thermal insulation. A few examples are shown in Figure.
The equation of state for an adiabatic process is given by
![]()
Here γ is called adiabatic exponent (γ = Cp/Cv) which depends on the nature of the gas. The equation (1) implies that if the gas goes from an equilibrium state (Pi, Vi) to another equilibrium state (Pf, Vf) adiabatically then it satisfies the relation
![]()
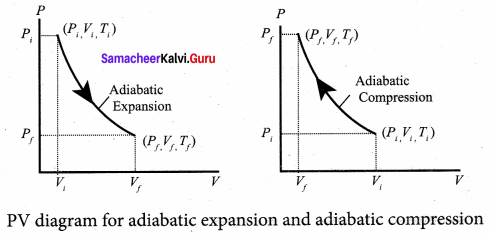
The PV diagram for an adiabatic process is also called adiabat. But actually the adiabatic curve is steeper than isothermal curve.
We can also rewrite the equation (1) in terms of T and V. From ideal gas equation, the pressure P = \(\frac{\mu \mathrm{RT}}{\mathrm{V}}\). Substituting this equation in the equation (1), we have
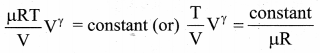
Note here that is another constant. So it can be written as
![]()
The equation implies that if the gas goes from an initial equilibrium state (Ti, Vi) to final equilibrium state (Tf, Vf) adiabatically then it satisfies the relation
![]()
The equation of state for adiabatic process can also be written in terms of T and P as
![]()
Question 16.
Derive the work done in an adiabatic process.
Answer:
Work done in an adiabatic process: Consider µ moles of an ideal gas enclosed in a cylinder having perfectly non conducting walls and base. A frictionless and insulating piston of cross sectional area A is fitted in the cylinder.
Let W be the work done when the system goes from the initial state (Pi, Vi, Ti) to the final state (Pf, Vf, Tf) adiabatically.
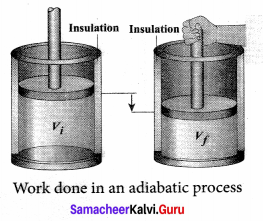
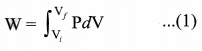
By assuming that the adiabatic process occurs quasi-statically, at every stage the ideal gas law is valid. Under this condition, the adiabatic equation of state is PVγ = constant (or)

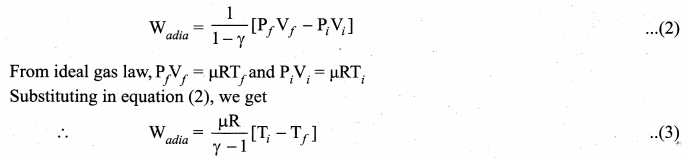
In adiabatic expansion, work is done by the gas. i.e., Wadia is positive. As Ti > Tf the gas
cools during adiabatic expansion.
In adiabatic compression, work is done on the gas. i.e., Wadia is negative. As Ti< Tf the
temperature of the gas increases during adiabatic compression.
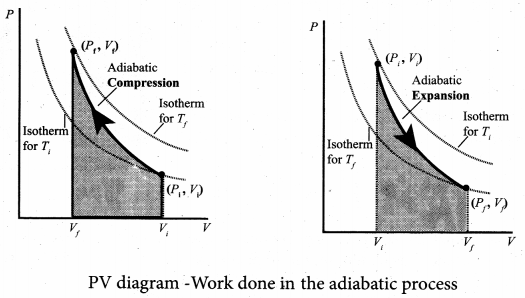
To differentiate between isothermal and adiabatic curves in PV diagram, the adiabatic curve is drawn along with isothermal curve for Tf and Ti. Note that adiabatic curve is steeper than isothermal curve. This is because γ > 1 always.
Question 17.
Explain the isobaric process and derive the work done in this process.
Isobaric process: This is a thermodynamic process that occurs at constant pressure. Even though pressure is constant in this process, temperature, volume and internal energy are not constant. From the ideal gas equation, we have
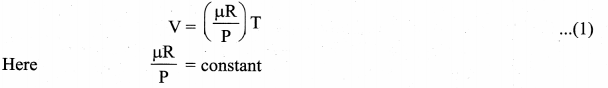
In an isobaric process the temperature is directly proportional to volume.
V ∝ T (Isobaric process) …. (2)
This implies that for a isobaric process, the V-T graph is a straight line passing through the origin.
If a gas goes from a state (Vi, Ti) to (Vf, Tf) at constant pressure, then the system satisfies the following equation

Examples for Isobaric process:
(i) When the gas is heated and pushes the piston so that it exerts a force equivalent to atmospheric pressure plus the force due to gravity then this process is isobaric.
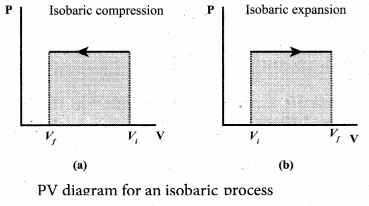
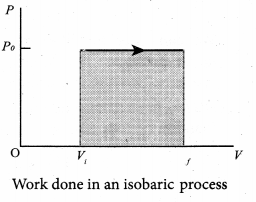
(ii) Most of the cooking processes in our kitchen are isobaric processes. When the food is cooked in an open vessel, the pressure above the food is always at atmospheric pressure. The PV diagram for an isobaric process is a horizontal line parallel to volume axis.
Figure (a) represents isobaric process where volume decreases figure
(b) represents isobaric process where volume increases.
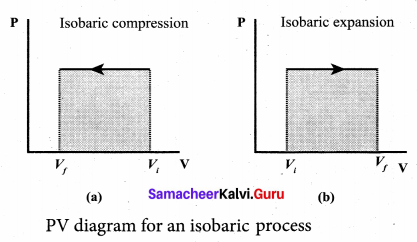
The work done in an isobaric process: Work done by the gas

In an isobaric process, the pressure is constant, so P comes out of the integral,
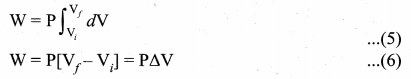
Where ∆V denotes change in the volume. If ∆V is negative, W is also negative. This implies that the work is done on the gas. If ∆V is positive, W is also positive, implying that work is done by the gas equation.
The equation (6) can also be rewritten using the ideal gas equation.
From ideal gas equation
![]()
Substituting this in equation (6) we get

In the PV diagram, area under the isobaric curve is equal to the work done in isobaric process. The shaded area in the above diagram is equal to the work done by the gas.
The first law of thermodynamics for isobaric process is given by

![]()
Question 18.
Explain in detail the isochoric process.
Answer:
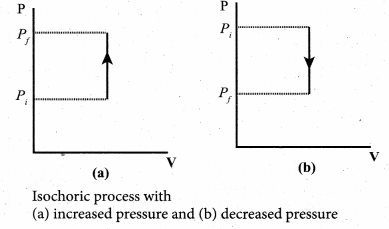
Isochoric process: This is a thermodynamic process in which the volume of the system is kept constant. But pressure, temperature and internal energy continue to be variables.
The pressure – volume graph for an isochoric process is a vertical line parallel to pressure axis as shown in Figure.
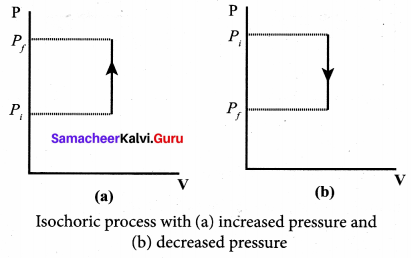
The equation of state for an isochoric process is given by
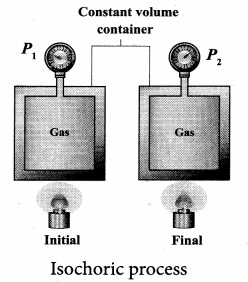
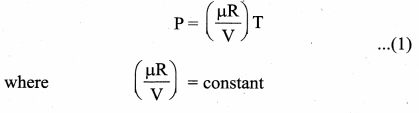
We can infer that the pressure is directly proportional to temperature. This implies that the P-T graph for an isochoric process is a straight line passing through origin. If a gas goes from state (Pi, Ti) to (Pf, Tf) at constant volume, then the system satisfies the following equation

For an isochoric processes, ∆V = 0 and W = 0. Then the first law becomes
∆U = Q …(3)
Implying that the heat supplied is used to increase only the internal energy. As a result the temperature increases and pressure also increases.
Suppose a system loses heat to the surroundings through conducting walls by keeping the volume constant, then its internal energy decreases. As a result the temperature decreases; the pressure also decreases.
Question 19.
What are the limitations of the first law of thermodynamics?
Answer:
Limitations of first law of thermodynamics: The first law of thermodynamics explains well the inter convertibility of heat and work. But it does not indicate the direction of change.
For example,
(a) When a hot object is in contact with a cold object, heat always flows from the hot object to cold object but not in the reverse direction. According to first law, it is possible for the energy to flow from hot object to cold object or from cold object to hot object. But in nature the direction of heat flow is always from higher temperature to lower temperature.
(b) When brakes are applied, a car stops due to friction and the work done against friction is converted into heat. But this heat is not reconverted to the kinetic energy of the car. So the first law is not sufficient to explain many of natural phenomena.
Question 20.
Explain the heat engine and obtain its efficiency.
Answer:
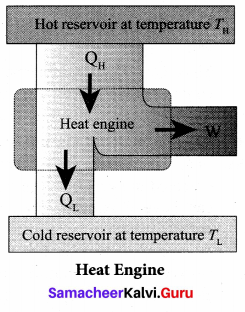
Heat Engine: In the modem technological world, the role of automobile engines plays a vital role in for transportation. In motor bikes and cars there are engines which take in petrol or diesel as input, and do work by rotating wheels. Most of these automobile engines have efficiency not greater than 40%. The second law of thermodynamics puts a fundamental restriction on efficiency of engines. Therefore understanding heat engines is very important.
Reservoir: It is defined as a thermodynamic system which has very large heat capacity. By taking in heat from reservoir or giving heat to reservoir, the reservoir’s temperature does not change.
Example: Pouring a tumbler of hot water in to lake will not increase the temperature of the lake. Here the lake can be treated as a reservoir.
When a hot cup of coffee attains equilibrium with the open atmosphere, the temperature of the atmosphere will not appreciably change. The atmosphere can be taken as a reservoir.
We can define heat engine as follows: Heat engine is a device which takes heat as input and converts this heat in to work by undergoing a cyclic process.
A heat engine has three parts:
(a) Hot reservoir
(b) Working substance
(c) Cold reservoir A Schematic diagram for heat engine is given below:
1. Hot reservoir (or) Source: It supplies heat to the engine. It is always maintained at a high temperature TH.
2. Working substance: It is a substance like gas or water, which converts the heat supplied into Work.
3. Cold reservoir (or) Sink: The heat engine ejects some amount of heat (QL) in to cold reservoir after it doing work. It is always maintained at a low temperature TL.
The heat engine works in a cyclic process. After a cyclic process it returns to the same state. Since the heat engine returns to the same state after it ejects heat, the change in the internal energy of the heat engine is zero.
The efficiency of the heat engine is defined as the ratio of the work done (out put) to the heat absorbed (input) in one cyclic process.
Let the working substance absorb heat QH units from the source and reject QL units to the sink after doing work W units.
We can write. Input heat = Work done + ejected heat
QH = W + QL
W = QH – QL
Then the efficiency of heat engine
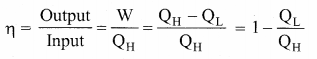
Note here that QH, QL and W all are taken as positive, a sign convention followed in this expression.
Since QL < QH, the efficiency (η) always less than 1. This implies that heat absorbed is not completely converted into work. The second law of thermodynamics placed fundamental restrictions on converting heat completely into work.
![]()
Question 21.
Explain in detail Carnot heat engine.
Answer:
In the year 1824 a young French engineer Sadi Carnot proved that a certain reversible engine operated in cycle between hot and cold reservoir can have maximum efficiency. This engine is called Carnot engine.
A reversible heat engine operating in a cycle between two temperatures in a particular way is called a Carnot Engine. The carnot engine has four parts which are given below.
(i) Source: It is the source of heat maintained at constant high temperature TH. Any amount of heat can be extracted from it, without changing its temperature.
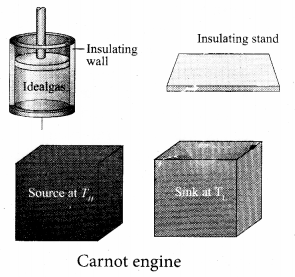
(ii) Sink: It is a cold body maintained at a constant low temperature TL. It can absorb any amount of heat.
(iii) Insulating stand: It is made of perfectly non-conducting material. Heat is not conducted through this stand.
(iv) Working substance: It is an ideal gas enclosed in a cylinder with perfectly non-conducting walls and perfectly conducting bottom. A non-conducting and frictionless piston is fitted in it.
Question 22.
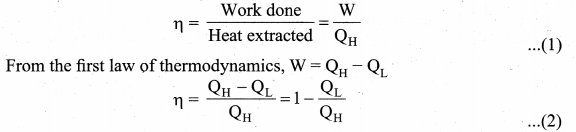
Derive the expression for Carnot engine efficiency.
Answer:
Efficiency of a Carnot engine: Efficiency is defined as the ratio of work done by the working substance in one cycle to the amount of heat extracted from the source.
Applying isothermal conditions, we get,
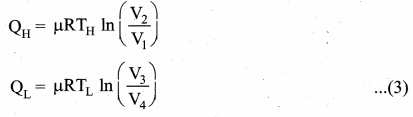
Here we omit the negative sign. Since we are interested in only the amount of heat (QL) ejected into the sink, we have
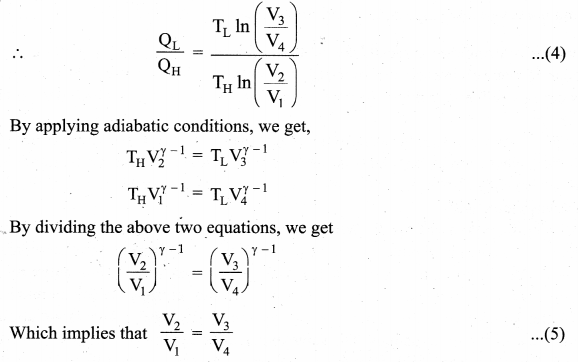
Substituting equation (5) in (4), we get
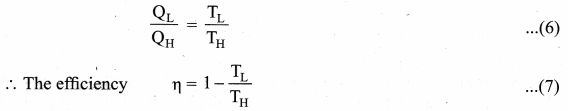
Note : TL and TH should be expressed in Kelvin scale.
Important results:
1. η is always less than 1 because TL is less than TH. This implies the efficiency cannot be 100%.
2. The efficiency of the Carnot’s engine is independent of the working substance. It depends only on the temperatures of the source and the sink. The greater the difference between the two temperatures, higher the efficiency.
3. When TH = TL the efficiency η = 0. No engine can work having source and sink at the same temperature.
Question 23.
Explain the second law of thermodynamics in terms of entropy.
Answer:
The quantity \(\frac{Q}{T}\) is called entropy. It is a very important thermodynamic property of a system.
It is also a state variable. \(\frac{\mathrm{Q}_{\mathrm{H}}}{\mathrm{T}_{\mathrm{H}}}\) is the entropy received by the Carnot engine from hot reservoir is entropy given out by the Carnot engine to the cold reservoir. For reversible engines (Carnot Engine) both entropies should be same, so that the change in entropy of the Carnot engine in one cycle is zero. But for all practical engines 1 ike diesel and petrol engines which are not reversible engines, they satisfy the relation \(\frac{\mathrm{Q}_{\mathrm{L}}}{\mathrm{T}_{\mathrm{L}}}>\frac{\mathrm{Q}_{\mathrm{H}}}{\mathrm{T}_{\mathrm{H}}}\)
In fact we can reformulate the second law of thermodynamics as follows “For all the processes that occur in nature (irreversible process), the entropy always increases. For reversible process entropy will not change”. Entropy determines the direction in which natural process should occur.
Entropy increases when heat flows from hot object to cold object. If heat were to flow from a cold to a hot object, entropy will decrease leading to violation of second law thermodynamics. Entropy is also called ‘measure of disorder’. All natural process occur such that the disorder should always increases.
Consider a bottle with a gas inside. When the gas molecules are inside the bottle it has less disorder. Once it spreads into the entire room it leads to more disorder. In other words when the gas is inside the bottle the entropy is less and once the gas spreads into entire room, the entropy increases. From the second law of thermodynamics, entropy always increases. If the air molecules go back in to the bottle, the entropy should decrease, which is not allowed by the second law of thermodynamics. The same explanation applies to a drop of ink diffusing into water. Once the drop of ink spreads, its entropy is increased. The diffused ink can never become a drop again. So the natural processes occur in such a way that entropy should increase for all irreversible process.
![]()
Question 24.
Explain in detail the working of a refrigerator.
Answer:
Refrigerator: A refrigerator is a Carnot’s engine working in the reverse order.
Working Principle: The working substance (gas) absorbs a quantity of heat QL from the cold body (sink) at a lower temperature TL. A certain amount of work W is done on the working substance by the compressor and a quantity of heat QH is rejected to the hot body (source) ie, the atmosphere at TH. When you stand beneath of refrigerator, you can feel warmth air. From the first law of thermodynamics, we have
QL + W = QH ….. (1)
As a result the cold reservoir (refrigerator) further cools down and the surroundings (kitchen or atmosphere) gets hotter.
Coefficient of performance (COP) (β): COP is a measure of the efficiency of a refrigerator. It is defined as the ratio of heat extracted from the cold body (sink) to the external work done by the compressor W.
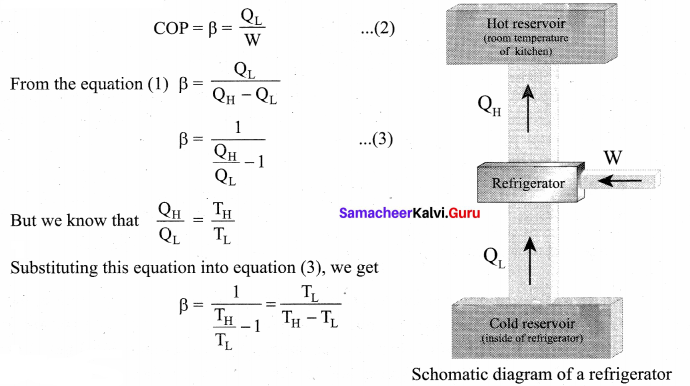
Inferences.
1. The greater the COP, the better is the condition of the refrigerator. A typical refrigerator has COP around 5 to 6.
2. Lesser the difference in the temperatures of the cooling chamber and the atmosphere, higher is the COP of a refrigerator.
3. In the refrigerator the heat is taken from cold object to hot object by doing external work. Without external work heat cannot flow from cold object to hot object. It is not a violation of second law of thermodynamics, because the heat is ejected to surrounding air and total entropy of (refrigerator + surrounding) is always increased.
Samacheer Kalvi 11th Physics Heat and Thermodynamics Numerical Problems
Question 1.
Calculate the number of moles of air is in the inflated balloon at room temperature as shown in the figure.

The radius of the balloon is 10 cm, and pressure inside the balloon is 180 kPa
Answer:

Question 2.
In the planet Mars, the average temperature is around – 53°C and atmospheric pressure is 0.9 kPa. Calculate the number of moles of the molecules in unit volume in the planet Mars? Is this greater than that in earth?
Answer:
T = – 53°C = 220 K
P = 0.9 × 103 Pa
V = 1 m3
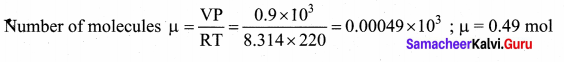
Question 3.
An insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume V1 and contains ideal gas at pressure P1 and temperature T1. The other chamber has volume V2 and contains ideal gas at pressure P2 and temperature T2. If the partition is removed without doing any work on the gases, calculate the final equilibrium temperature of the container.
Answer:
Let T be the equilibrium temperature and let n1 and n2 be the number of moles in vessels 1 and 2 respectively. As there is no loss of energy,
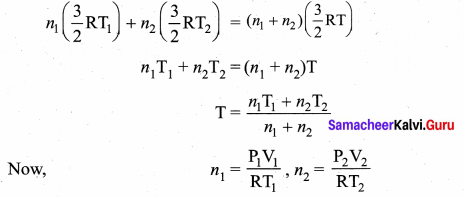
Substituting n1 and n2 values and solving, we get
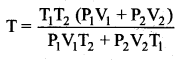
Question 4.
The temperature of a uniform rod of length L having a coefficient of linear expansion αL is changed by ∆T. Calculate the new moment of inertia of the uniform rod about axis passing through its center and perpendicular to an axis of the rod.
Answer:
Moment of inertia of a uniform rod of mass and length l about its perpendicular bisector. Moment of inertia of the rod

Increase in length of the rod when temperature is increased by ∆T, is given by
L’ = L(1 + αL∆T)
New moment of inertia of the rod
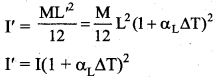
Question 5.
Draw the TP diagram (P – x axis, T – y axis), VT(T – x axis, V – y axis) diagram for
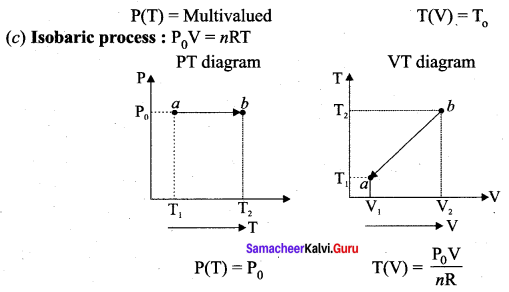
(a) Isochoric process
(b) Isothermal process
(c) Isobaric process
Answer:
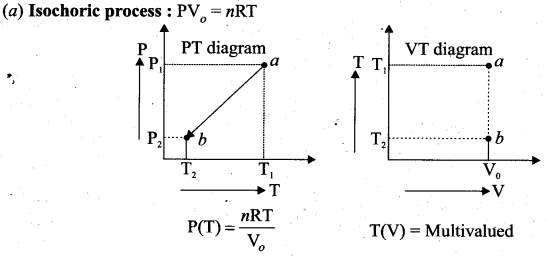
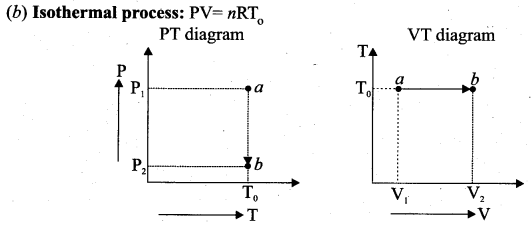
Question 6.
A man starts bicycling in the morning at a temperature around 25°C, he checked the pressure of tire which is equal to be 500 kPa. Afternoon he found that the absolute pressure in the tyre is increased to 520 kPa. By assuming the expansion of tyre is negligible, what is the temperature of tyre at afternoon?
Answer:
For ideal gas equation of state
PV = nRT
P1 = 500 kPa, T1 = 25°C = 25 + 273 = 298K, P2 = 520 kPa, T2 = ?
Expansion of tyre is negligible (Vconstant)
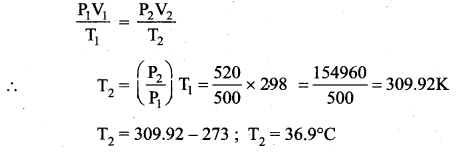
Question 7.
Normal human body of the temperature is 98.6°F. During high fever if the temperature increases to 104°F, what is the change in peak wavelength that emitted by our body? (Assume human body is a black body).
Answer:
Normal human body temperature (T) = 98.6°F
Convert Fahrenheit into Kelvin,
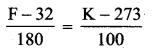
So, T = 98.6° F = 310 K
From Wien’s displacement law
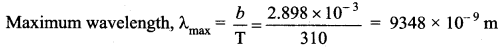

Question 8.
In an adiabatic expansion of the air, the volume is increased by 4%, what is percentage change in pressure? (For air γ = 1.4)
Answer:
From equation for adiabatic process,

Question 9.
In a petrol engine, (internal combustion engine) air at atmospheric pressure and temperature of 20°C is compressed in the cylinder by the piston to 1/8 of its original volume. Calculate the temperature of the compressed air. (For air γ = 1.4)
Answer:

Question 10.
Consider the following cyclic process consist of isotherm, isochoric and isobar which is given in the figure.
Draw the same cyclic process qualitatively in the V-T diagram where T is taken along x – direction and V is taken along y – direction. Analyze the nature of heat exchange in each process.
Answer:
Process 1 to 2 = increase in volume. So heat must be added.
Process 2 to 3 = Volume remains constant. Increase in temperature.
The given heat is used to increase the internal energy.
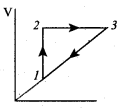
Process 3 to 1 : Pressure remains constant. Volume and Temperature are reduced. Heat flows out of the system.
It is an isobaric compression where the work is done on the system.
![]()
Question 11.
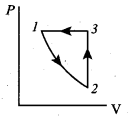
An ideal gas is taken in a cyclic process as shown in the figure.
Calculate
(a) work done by the gas.
(b) work done on the gas
(c) Net work done in the process
Answer:
(a) Work done by the gas (along AB)
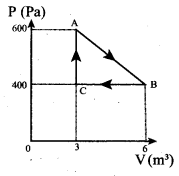
(c) Net work done in the process = Area under the curve AB
= Rectangle area + triangle area
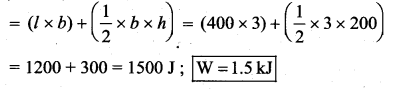
Question 12.
For a given ideal gas 6 × 105J heat energy is supplied and the volume of gas is increased from 4 m3 to 6 m3 at atmospheric pressure. Calculate
(a) the work done by the gas
(b) change ¡n internal energy of the gas
(c) graph this process ¡n PV and TV diagram.
Answer:
Heat energy supplied to gas Q = 6 × 105J
Change in volume ∆V = (6 – 4) = 2 m3
1 atm = 1.0 13 × 105 Nm-2
(a) Work done by the gas W = P × ∆V = 1.013 × 105 × 2 = 2.026 × 105
W = 202.6kJ1
(b) Change in internal energy of the gas
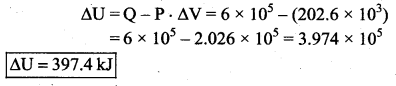
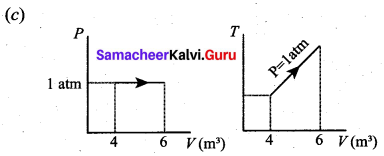
Question 13.
Suppose a person wants to increase the efficiency of the reversible heat engine that is operating between 100°C and 300°C. He had two ways to increase the efficiency,
(a) By decreasing the cold reservoir temperature from 100°C to 50°C and keeping the hot reservoir temperature constant
(b) by increasing the temperature of the hot reservoir from 300°C to 350°C by keeping the cold reservoir temperature constant. Which is the suitable method?
Answer:
Heat engine operates at initial temperature = 100°C + 273 = 373 K
Final temperature = 300°C + 273 = 573 K
At melting point = 273 K
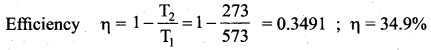
(a) By decreasing the cold reservoir, efficiency
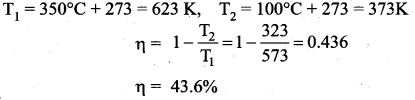
(b) By increasing the temperature of hot reservoir, efficiency,
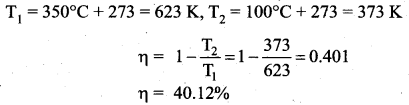
Method (a) More efficiency than method (b).
Question 14.
A Carnot engine whose efficiency is 45% takes heat from a source maintained at a temperature of 327°C. To have an engine of efficiency 60% what must be the intake temperature for the same exhaust (sink) temperature?
Answer:
Efficiency of Carnot engine (η1) = 45% = 0.45
Initial intake temperature (T1) = 327°C = 600 K
New efficiency (η2) = 60% = 0.6
Efficiency of Carnot engine is given by
![]()
T1 is temperature of source ; T2 is temperature of sink

Question 15.
An ideal refrigerator keeps its content at 0°C while the room temperature is 27°C. Calculate its coefficient of performance.
Answer:

Samacheer Kalvi 11th Physics Heat and Thermodynamics Textual Evaluation Solved Additional Questions Solved
I. Choose the correct answer from the following:
Question 1.
The coefficient of volume expansion of a solid is x times the coefficient of superficial expansion. Then x is
(a) 1.5
(b) 2
(c) 2.5
(d) 3
Answer:
(a) 1.5
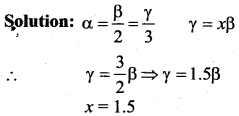
Question 2.
A solid metal ball has a spherical cavity. If the ball is heated, the volume of the cavity will
(a) increase
(b) decrease
(c) remain unaffected
(d) remain unaffected but the shape of the cavity will change.
Answer:
(a) increase
Question 3.
A metal sheet with a circular hole is heated. The hole will
(a) contract
(b) expand
(c) remain unaffected
(d) contract or expand depending on the value of the linear expansion coefficient.
Answer:
(b) expand
Question 4.
The length of a metal rod at 0°C is 0.5m. When it is heated, its length increases by 2.7 mm. The final temperature of the rod is (coefficient of linear expansion of the metal = 90 × 106/°C) ……
(a) 20°C
(b) 30°C
(c) 40°C
(d) 60°C
Answer:
(d) 60°C
Solution:
lt = l0(1 + αt)
![]()
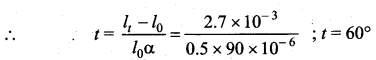
Question 5.
A bimetal made of copper and iron strips welded together is straight at room temperature. It is held vertically with iron strip towards left and copper strip towards right. If this bimetal is heated, it will
(a) remain straight
(b) bend towards right
(c) bend towards left
(d) bend forward
Answer:
(c) bend towards left
Solution:
Since αcopper > αiron, the bimetal will bend towards iron, i.e., towards left.
![]()
Question 6.
When water is heated from 0°C to 10°C, its volume …..
(a) decreases
(b) increases
(c) first increase and then decrease
(d) first decreases and then increases.
Answer:
(d) first decreases and then increases.
Question 7.
A block of wood is floating on water at 0°C with a certain volume V above water level. The temperature of water is slowly raised to 20°C. How does the volume V change with the rise of temperature?
(a) remain unchanged
(b) decrease continuously
(c) decrease till 4°C and then increase
(d) increase till 4°C and then decrease.
Answer:
(a) increase till 4°C and then decrease.
Solution:
The density of water increases from 0° to 4°C and then decreases. Therefore, the volume V of the block above water level will increase till 4°C and then decrease.
Question 8.
An iron tyre is to be fitted on a wooden wheel 0.1m in diameter. The diameter of the tyre is 6 mm smaller than that of the wheel. The tyre should be heated by a temperature of (coefficient of volume expansion of iron is 3.6 × 10-5/°C)
(a) 167°C
(b) 334°C
(c) 500°C
(d) 1000°C
Answer:
(a) 167°C
Solution:
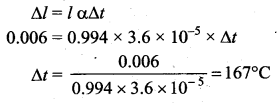
Question 9.
A steel rod of length 25 cm has a cross-sectional area of 0.8 cm2. The force required to stretch this rod by the same amount as the expansion produced by heating it through 10°C is (coefficient of linear expansion of steel is 10 51°C and Young’s modulus of steel is 2 × 1010 N/m2) …….
(a) 40 N
(b) 80 N
(c) 120 N
(d) 160 N
Answer:
(d) 160N
Solution:
The required force is given by
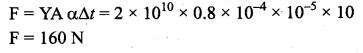
Question 10.
Which of the following will make the volume of an ideal gas four times?
(a) double the absolute temperature and double the pressure.
(b) Halve the absolute temperature and double the pressure.
(c) Quarter the absolute temperature at constant pressure.
(d) Quarter the pressure at constant temperature.
Answer:
(d) Quarter the pressure at constant temperature.
Question 11.
A perfect gas at 27°C is heated at constant pressure so as to double its volume. The temperature of the gas becomes.
(a) 54° C
(b) 150 K
(c) 327° C
(d) 327 K
Answer:
(c) 327°C
Solution:
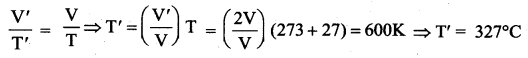
Question 12.
An air bubble doubles in radius on rising from the bottom of a lake to its surface. If the atmospheric pressure is equal to that of a column of water of height H, the depth of lake is
(a) H
(b) 2H
(c) 7H
(d) 8H
Answer:
(c) 7H
Solution:
Since the radius becomes double, the volume becomes eight times. Therefore, according to Boyle’s law, the pressure becomes one-eighth. Now, the pressure at the surface Hρg. Therefore pressure at the bottom must be 8 Hρg. Hence the depth of the lake is 7H.
![]()
Question 13.
The mass of 1 litre of helium under a pressure of 2 atm and at a temperature of 27°C is
(a) 0.16 g
(b) 0.32 g
(c) 0.48 g
(d) 0.64 g
Answer:
(b) 0.32 g
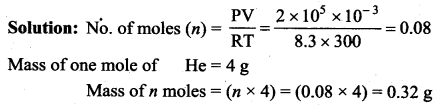
Question 14.
Pressure exerted by a perfect gas is equal to …….
(a) mean kinetic energy per unit volume
(b) half of mean kinetic energy per unit volume
(c) one-third of mean kinetic energy per unit volume
(d) two-thirds of mean kinetic energy per unit volume
Answer:
(d) two-thirds of mean kinetic energy per unit volume
![]()
Question 15.
Two vessels A and B contain the same ideal gas. The volume of B is twice that of A, the pressure in B is twice that in A and the temperature of B is twice that of A. The ratio of the number of gas molecules in A and B is
(a) 1 : 2
(b) 2 : 1
(c) 1 : 4
(d) 4 : 1
Answer:
(a) 1 : 2
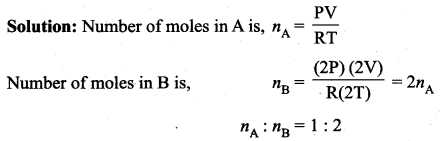
Question 16.
According to Boyle’s law, PV = C when the temperature of the gas remains constant. The value of C depends on
(a) temperature of the gas
(b) nature of the gas
(c) quantity of the gas
(d) both temperature and quantity of the gas.
Answer:
(d) both temperature and quantity of the gas.
Question 17.
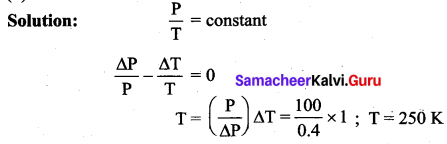
The pressure of a gas contained in a closed vessel is increased by 0.4% when heated by 1°C. The initial temperature was
(a) 250 K
(b) 250°C
(c) 25 K
(d) 25°C
Answer:
(c) 25 K
Question 18.
A temperature difference of 25°C is equivalent to a temperature difference of
(a) 25°F
(b) 45°F
(c) 67°F
(d) 77°F
Answer:
(b) 45°F
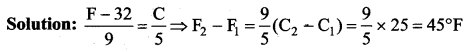
Question 19.
A temperature at which both the Fahrenheit and the centigrade scales have the same value is
(a) 40°
(b) -40°
(c) 20
(d) – 20°
Answer:
(b) – 40°
Solution: Let the required temperature be t. then, \(\frac{t}{5}=\frac{t-32}{9} \Rightarrow t=-40^{\circ}\)
Question 20.
If the temperature of patient is 40°C, his temperature on the Fahrenheit scale will be
(a) 72°F
(b) 96°F
(c) 100°F
(d) 104°F
Answer:
(d) 104°F
![]()
Question 21.
The correct value of 0°C on the Kelvin scale is ……..
(a) 273.15 K
(b) 272.85 K
(c) 273 K
(d) 273.2 K
Answer:
(a) 273.15 K
![]()
Question 22.
When a gas in a closed vessel was heated so as to increase its temperature by 5°C, there occurred an increase of 1% in its pressure, the original temperature of the gas was …….
(a) 50°C
(b) 227°C
(c) 273°C
(d) 500°C
Answer:
(b) 227°C
![]()
Question 23.
A perfect gas at 27°C is heated at constant pressure so as to double its volume. The temperature of the gas will be …….
(a) 600°C
(b) 54°C
(c) 327°C
(d) 300°C
Answer:
(c) 327°C
![]()
Question 24.
Temperature can be expressed as a derived quantity in terms of ……
(a) length and mass
(b) mass and time
(c) length, mass and time
(d) none of these
Answer:
(d) none of these
Question 25.
The equation of state corresponding to 8 g of O2 is
(a) PV = 8RT
(b) PV = RT/4
(c) PV = RT
(d) PV = RT/2
Answer:
(b) PV = RT/4
Solution:
8g of O2 is 1/4 of a mole of O2, which is 32g. Thus, the required equation of state is PV = \(\frac{1}{4} \mathbf{R} \mathbf{T}\).
Question 26.
At a given volume and temperature, the pressure of a gas ….
(a) varies inversely as its mass
(b) varies inversely as the square of its mass
(c) varies linearly as its mass
(d) is independent of its mass
Answer:
(c) varies linearly as its mass
Question 27.
Oxygen boils at -183°C. This temperature in Fahrenheit scale is
(a) -215.7°
(b) – 297.4°
(c) -310.6°
(d) – 373.2°
Answer:
(b) – 297.4°
Solution:
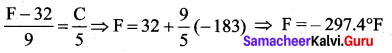
Question 28.
A centigrade and a Fahrenheit thermometer are dipped in boiling water. The water temperature is lowered until the Fahrenheit thermometer registers 140°. What is the decrease in temperature as registered by the centigrade thermometer?
(a) 80°
(b) 60°
(c) 40°
(d) 30°
Answer:
(c) 40°
Solution:
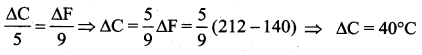
Question 29.
The change in temperature of a body is 50°C. The change on the kelvin scale is …….
(a) 50K
(b) 323K
(c) 70K
(d) 30K
Answer:
(a) 50K
Question 30.
Mercury thermometers can be used to measure temperature up to ……..
(a) 260°C
(b) 100°C
(c) 360°C
(d) 500°C
Answer:
(c) 360°C
Question 31.
For an ideal gas the inter particle interaction is ……..
(a) attractive
(b) repulsive
(c) very large
(d) zero
Answer:
(d) zero
Question 32.
Device used to measure very high temperature is …….
(a) Pyrometer
(b) Thermometer
(c) Bolometer
(d) calorimeter
Answer:
(a) Pyrometer
Question 33.
Two metal rods A and B are having their initial lengths in the ratio 2 : 3, and coefficients of linear expansion in the ratio 3 : 4. When they are heated through same temperature difference,the ratio of their linear expansions is ……
(a) 1 : 2
(b) 2 : 3
(c) 3 : 4
(d) 4 : 3
Answer:
(a) 1 : 2
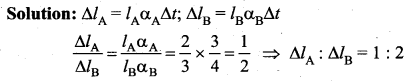
Question 34.
Boyles’ law is applicable in ……
(a) isochoric process
(b) isothermal process
(c) isobaric process
(d) both (a) and (b)
Answer:
(b) isothermal process
Question 35.
A rod, when heated from 0°C to 50°C, expands by 1.0 mm. Another rod, twice as long as the first at 0°C and of the same material, is heated from 0°C to 25°C. The second rod will expand by ……
(a) 0.5 mm
(b) 1.0 mm
(c) 2.0 mm
(d) 4.0 mm
Answer:
(b) 1.0 mm
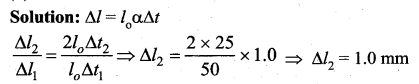
Question 36.
A container contains hydrogen gas at pressure P and temperature T. Another identical container contains helium gas at pressure 2P and temperature T/2. The ratio of the number of molecules of the two gases is
(a) 1 : 4
(b) 4 : 1
(c) 1 : 2
(d) 2 : 1
Answer:
(a) 1 : 4
Solution:
The ratio of the number of molecules is same as the ratio of the number of moles.
Now n = \(\frac{P V}{R T}\)
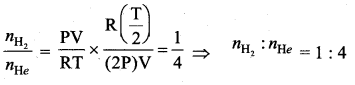
Question 37.
Density of water is maximum at the temperature of
(a) 32°F
(b) 39.2°F
(c) 42°F
(d) 40°F
Answer:
(b) 39.2°F
Solution:
The density of water is maximum at 4°C. Let F be the corresponding temperature on the Fahrenheit scale. Then using the equation
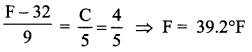
![]()
Question 38.
The equation of state for 5 g of oxygen at a pressure P and temperature T, when occupying a volume V, is (R is the gas constant) …….
(a) PV = (5/32) RT
(b) PV = 5RT
(c) PV = (5/2)RT
(d) PV = (5/16)RT
Answer:
(a) PV = (5/32) RT
Solution:
Number of moles, n = \(\frac{5}{32}\)
Question 39.
A bimetallic strip consists of metals X and Y. It is mounted rigidly at the base as shown. The metal X has a higher coefficient of expansion compared to that for metal Y. When the bimetallic strip is placed in a cold bath?
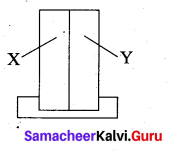
(a) it will bend towards the right
(b) it will bend towards the left
(b) it will not bend but shrink
(d) it will neither bend nor shrink
Answer:
(b) it will bend towards the left.
Solution:
In cold bath, the metal X will contract more than the metal Y. Therefore, the strip will bend towards the left.
Question 40.
An ideal gas is expanding such that PT2 = constant the coefficient of volume expansion of the gas is
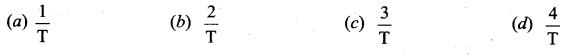
Answer:
\(\frac{3}{\mathrm{T}}\)
Solution:
Coefficient of volume expansion \(\alpha_{\mathrm{v}}=\frac{d \mathrm{V}}{\mathrm{v} d \mathrm{T}}\)
PT2 = K and PV = nRT
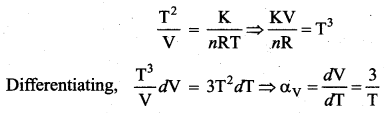
Question 41.
A metallic solid sphere is rotating about its diameter as axis of rotation. If the temperature is increased by 200°C, the percentage increase in its moment of inertia is : (coefficient of linear expansion of the metal = 10-5/°C)
(a) 0.1
(b) 0.2
(c) 0.3
(d) 0.4
Answer:
(d) 0.4
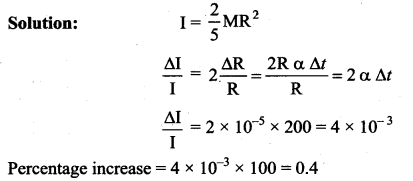
Question 42.
The difference between volume and pressure coefficients of an ideal gas is ……
![]()
Answer:
(d) Zero
Question 43.
Which of the following instruments is used in the measurement of temperatures above 2000°C?
(a) Gas thermometer
(b) Pyrometer
(c) Bolometer
(d) Thermo-electric Pile
Answer:
(b) Pyrometer
![]()
Question 44.
At 0°C, Pressure measured by barometer is 760 mm. What will be the pressure at 100°C?
(a) 760
(b) 730
(c) 780
(d) none of these
Answer:
(d) none of these
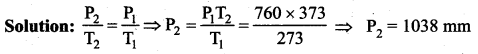
Question 45.
The temperature on the new scale, corresponding to a temperature of 39°C on the Celsius scale?
(a) 73°W
(b) 117°W
(c) 200°W
(d) 139°W
Answer:
(b) 117°W
Solution:
Let t be the required temperature. Then,
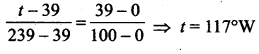
Question 46.
Two balloons are filled, one with pure He gas and the other with air. If the pressure and temperature in both the balloons are same the number of molecules per unit volume is
(a) more in the He filled balloon
(b) more in the air filled balloon.
(c) same in both the balloon.
(d) in the ratio 1 : 4.
Answer:
(c) same in both the balloons.
Solution: Assuming ideal gas behavior, the number of moles per unit volume is \(\frac{n}{\mathrm{V}}=\frac{\mathrm{P}}{\mathrm{RT}}\) Since P and T are same in both the balloon, \(\frac{n}{V}\) is also same in both.
Question 47.
Pressure of an ideal gas is increased by keeping temperature constant. What is the effect on the kinetic energy of molecules?
(a) increase
(b) no change
(c) decrease
(d) can’t be determined
Answer:
(b) no change
Solution:
K.E of an ideal gas depends only on the temperature. Hence, it remains the same.
Question 48.
One mole of gas occupies a volume of 200 ml. at 100 mm pressure. What is the volume occupied by two moles of this gas at 400 mm pressure and at same temperature?
(a) 50 ml
(b) 100 ml
(c) 200 ml
(d) 400 ml
Answer:
(b) 100 ml
Solution:
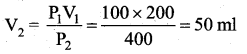
⇒ Volume of 2 moles of the gas at 400 mm pressure = 2 × 50 = 100 ml
Question 49.
There is a change in length when a 33000 N tensile force is applied on a steel rod of area of cress-section 10-3 m2. The change of temperature required to produce the same elongation, if the steel rod is heated, is (modulus of elasticity of steel = 3 × 1011 N/m2, coefficient of linear expansion of steel = 1.1 × 10-5/°C) …….
(a) 20°C
(b) 15°C
(c) 10°C
(d) 0°C
Answer:
(c) 10°C
Solution:
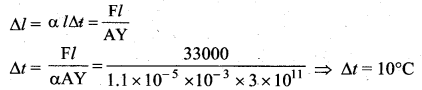
Question 50.
In the given (V – T) diagram, what is the relation between pressures P1 and P2?
(a) P2 = P1
(b) P2 > P1
(c) P2 < P1
(d) cannot be predicted
Answer:
(c) P2 < P1
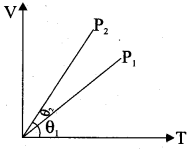

![]()
Question 51.
Boiling water is changing into steam. Under this condition the specific heat of water is
(a) zero
(b) one
(c) infinite
(d) less than one
Answer:
(c) infinite
Solution:
In order to change boiling water into steam, heat has to be given but there is no increase of temperature. Therefore, under this condition the specific heat of water is infinite.
Question 52.
The first law of thermodynamics is concerned with the conservation of ……
(a) number of molecules
(b) energy
(c) number of moles
(d) temperature
Answer:
(b) energy
Question 53.
The gas law \(\frac{P V}{T}\) = constant is true for
(a) isothermal changes only
(b) adiabatic changes only
(c) both isothermal and adiabatic changes
(d) neither isothermal nor adiabatic changes
Answer:
(c) both isothermal and adiabatic changes
Question 54.
The pressure-temperature relationship for an ideal gas undergoing adiabatic change is …..

Answer:
(a) \(\mathrm{p}^{1-\gamma} \mathrm{T}^{\gamma}\) = constant
Question 55.
For a certain gas the ratio of specific heats is given to be γ = 1.5. For this gas ……..
(a) Cv = 3R
(b) CP = 3R
(c) CV = 5R
(d) CP = 5R
Answer:
(b) CP = 3R
Solution:
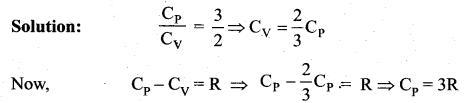
Question 56.
Cooking takes longest time ………
(a) at the sea level
(b) at Shimla
(c) at mount Everest (if tried)
(d) in a submarine 100 m below the surface of water.
Answer:
(c) at mount Everest (if tried)
Question 57.
A closed bottle containing water at room temperature is taken to the moon and then the lid is opened. The water will ……
(a) freeze
(b) boil
(c) decompose into hydrogen and oxygen
(d) not change at all.
Answer:
(b) boil
Solution:
There is no atmosphere on the moon and so there is no pressure
Quarter 58.
A gas receives an amount of heat equal to 110 joules and performs 40 joules of work. The change in the internal energy of the gas is …….
(a) 70 J
(b) 150 J
(c) 110 J
(d) 40 J
Answer:
(a) 70 J
![]()
Question 59.
For a mono-atomic gas, the molar specific heat at constant pressure divided by the molar gas constant R, is equal to ……
(a) 2.5
(b) 1.5
(c) 5.0
(d) 3.5
Answer:
(a) 2.5
Question 60.
Heat capacity of a substance is infinite. It means …….
(a) infinite heat is given out
(b) infinite heat is taken in
(c) no change in temperature whether heat is taken in or given out
(d) all of these
Answer:
(c) no change in temperature whether heat is taken in or given out
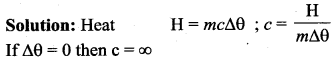
Question 61.
We consider a thermodynamic system. If ∆U represent the increase in its energy and W the work done by the system, which of the following statements is true?
(a) ∆U = – W in an isothermal process
(b) ∆U = – W in an adiabatic process
(c) ∆U = W in an isothermal process
(d) ∆U = W in an adiabatic process
Answer:
(b) ∆U = – W in an adiabatic process
Solution:
According to the first law of thermodynamics ∆Q = AU + W
In an adiabatic process, ∆Q = 0. Therefore, ∆U = – W
Question 62.
The first operation involved in a carnot cycle is
(a) isothermal expansion
(b) adiabatic expansion
(c) isothermal compression
(d) adiabatic compression
Answer:
(a) isothermal expansion
Question 63.
During an adiabatic process, if the pressure of an ideal gas is proportional to the cube of its temperature, the ratio \(\gamma=\frac{\mathrm{C}_{\mathrm{P}}}{\mathrm{C}_{\mathrm{V}}}\) is ….

Answer:
(d) \(\frac{3}{2}\)
Solution:

Question 64.
In a given process on an ideal gas, dW = 0 and dQ < 0. Then for the gas ……..
(a) The temperature will decrease.
(b) the volume will decrease.
(c) the pressure will remain constant.
(d) the temperature will increase.
Answer:
(a) The temperature will decrease.
Solution:
According to the first law of thermodynamics, the internal energy decreases. Hence the temperature will decrease.
Question 65.
In a carnot heat engine 8000J of heat is absorbed from a source at 400 K and 6500 J of heat is rejected to the sink. The temperature of the sink is …..
(a) 325 K
(b) 100 K
(c) 200 K
(d) 273 K
Answer:
(a) 325 K
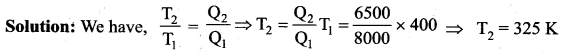
Question 66.
2 Kg of water of 60°C is mixed with 1 kg of water at 30°C kept in a vessel of heat capacity 220 J K-1. The specific heat of water is 4200 J Kg-1K ‘. Then the final temperature is nearly.
(a) 35°C
(b) 45°C
(c) 55°C
(d) 50°C
Answer:
(d) 50°C
Solution:
According to the principle of calorimetry,
![]()
![]()
Question 67.
A carnot engine absorbs heat at 127°C and rejects heat at 87°C. The efficiency of engine is
(a) 10%
(b) 30%
(c) 50%
(d) 70%
Answer:
(a) 10%
Solution:
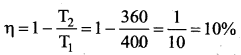
Question 68.
The first law of thermodynamics confirms the law of ……
(a) conservation of momentum
(b) conservation of energy
(c) flow of heat in a particular direction
(d) conservation of heat energy and mechanical energy
Answer:
(b) conservation of energy
Question 69.
The internal energy of an ideal gas depends on
(a) only pressure
(b) only volume
(c) only temperature
(d) none of these
Answer:
(c) only temperature
Question 70.
An ideal gas heat engine operators in a carnot’s cycle between 227°C and 127°C. It absorbs 6 × 104J at high temperature. The amount of heat converted into work is
(a) 2.4 × 104 J
(b) 4.8 × 104J
(c) 1.2 × 104J
(d) 6 × 104J
Answer:
(c) 1.2 × 104J
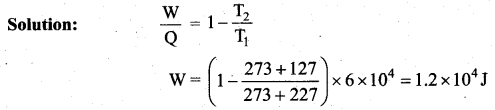
Question 71.
In an isochoric process
(a) ∆U = ∆Q
(b) ∆Q = ∆W
(c) ∆U = ∆W
(d) None of these
Answer:
(a) ∆U = ∆Q
Solution:
In an isochoric process, volume remains constant. Therefore, no work is done by or on the system. So, ∆W = 0 Hence ∆U = ∆Q.
Question 72.
The molar specific heat at constant pressure of an ideal gas is (7/2) R. The ratio specific heats at constant pressure to that at constant volume is ………
(a) 8/7
(b) 5/7
(c) 9/7
(d) 7/5
Answer:
(d) 7/5
Solution:
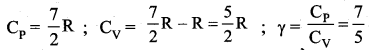
Question 73.
If energy dQ is supplied to a gas isochorically, increase in internal energy is dU. Then ….
(a) dQ > dU
(b) dQ < dU
(c) dQ = dU
(d) dQ = -dU
Answer:
(c) dQ = dU
Question 74.
A diatomic ideal gas is used in a camot engine as the working substance. If during the adiabatic expansion part of the cycle, the volume of the gas increases from V to 32 V, the efficiency of the engine is ……
(a) 0.25
(b) 0.5
(c) 0.75
(d) 0.99
Answer:
(c) 0.75

Question 75.
The mechanical equivalent of heat J is:
(a) a constant
(b) a physical quantity
(c) a conversion factor
(d) none of the above
Answer:
(c) a conversion factor
Question 76.
Which of the following process is reversible?
(a) transfer of heat by radiation
(b) Transfer of heat by conduction
(c) Electrical heating of nichrome wire
(d) Isothermal compression
Answer:
(d) Isothermal compression
Question 77.
An ideal gas heat engine operates in camot cycle between 227°C and 127°C. It absorbs 6 × 104 cal of heat converted to work is ……
(a) 1.2 × 104 cal
(b) 4.8 × 104 cal
(c) 6 × 104 cal
(d) 2.4 × 104 cal
Answer:
(a) 1.2 × 104 cal
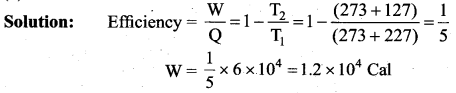
Question 78.
Ten moles of an ideal gas at constant temperature 600 K is compressed from 100 l to 10 L. The work done in the process is …..
(a) 4.11 × 104 J
(b) -4.11 × 104 J
(c) 11.4 × 104 J
(d) – 11.4 × 104 J
Answer:
(d) -11.4 × 104 J
Solution:
The process is isothermal. The work done is,
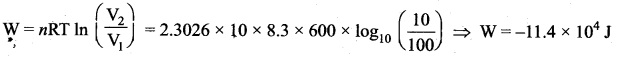
Question 79.
A gas is compressed at a constant pressure of 50 N/m2 from a volume 4 m3. Energy of 100 J is then added to the gas by heating. Its internal energy is …..
(a) increased by 400 J
(b) increased by 200 J
(c) increased by 100 J
(d) decreased by 200 J
Answer:
(a) increased by 400 J
Solution:
∆U = ∆Q – ∆W = ∆Q – P∆V = 100 – 50 (4 – 10) = 400 J
![]()
Question 80.
If Q, E and W denote respectively the heat added, change in internal energy and the work done in a closed cyclic process, then ……
(a) W = 0
(b) Q = W = O
(c) E = 0
(d) Q = 0
Answer:
(c) E = 0
Solution:
In a cyclic process, a system starts in one state and comes back to the same state. Therefore, the change in internal energy is zero.
Question 81.
A carnot engine takes heat from a reservoir at 627°C and rejects heat to a sink at 27°C. Its efficiency is
(a) 3/5
(b) 1/3
(c) 2/3
(d) 200/209
Answer:
(c) 2/3
Question 82.
A carnot engine operates with source at 127°C and sink at 27°C. If the source supplies 40 KJ of heat energy, the work done by the engine is
(a) 1 KJ
(b) 4 KJ
(c) 10 KJ
(d) 30 KJ
Answer:
(c) 10 KJ
Solution:
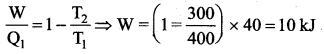
Question 83.
The ratio of the specific heat \(\frac{\mathrm{C}_{\mathrm{p}}}{\mathrm{C}_{\mathrm{v}}}=\gamma\) in term of degrees of freedom (n) is given by:
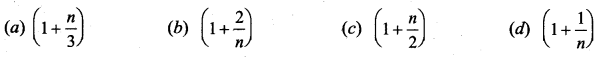
Answer:
(b) \(\left(1+\frac{2}{n}\right)\)
Solution:
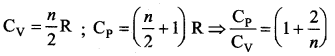
Question 84.
The heat required to increase the temperature of 4 moles of a mono-atomic ideal gas from 273 K to 473 K constant volume is ….
(a) 200 R
(b) 400 R
(c) 800 R
(d) 1200 R
Answer:
(d) 1200 R
Solution:
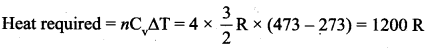
![]()
Question 85.
The coefficient of performance of a refrigerator is 5. If the temperature inside freezer is – 20°C, the temperature of the surroundings to which it rejects heat is ……
(a) 21°C
(b) 31°C
(c) 41°C
(d) 11°C
Answer:
(b) 31°C
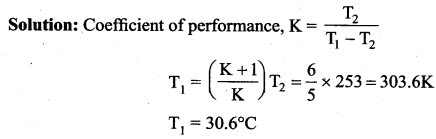
II. Write brief answer to the following questions:
Question 1.
What is meant by ‘heat’?
Answer:
When an object at higher temperature is placed in contact with another object at lower temperature, there will be a spontaneous flow of energy from the object at higher temperature to the one at lower temperature. This energy is called heat.
Question 2.
What is meant by ‘temperature’? Give its unit.
Answer:
Temperature is the degree of hotness or coolness of a body. Hotter the body higher is its temperature. The temperature will determine the direction of heat flow when two bodies are in thermal contact. The SI unit of temperature is kelvin (K).
Question 3.
Define Avogadro’s number NA?
Answer:
The Avogadro’s number NA is defined as the number of carbon atoms contained in exactly 12g of 12C
Question 4.
Define heat capacity (or) thermal capacity?
Answer:
The heat capacity of a body is defined as the amount of heat required to raise its temperature through one degree.
![]()
Question 5.
What is meant by ‘Triple point of a substance’?
Answer:
The triple point of a substance is the temperature and pressure at which the three phases (gas, liquid and solid) of that substance coexist in thermodynamic equilibrium.
Question 6.
What do you meant by change of state of a substance?
Answer:
The transition of a substance from one state to another by heating or cooling it is called change of state.
Question 7.
Define coefficient of linear expansion. Give its unit.
Answer:
The coefficient of linear expansion of the material of a solid rod is defined as the increase in length per unit original length per degree rise in its temperature.
The unit of αL is °C-1 (or KT-1)
Question 8.
Define coefficient of area expansion? Give its unit.
Answer:
The coefficient of area expansion of a metal sheet is defined as the increase in its surface area per unit original surface area per degree rise in its temperature.
The unit of αA is °Cα-1 (or) KT-1
Question 9.
Define coefficient of Volume expansion? Give its unit.
Answer:
The coefficient of Volume expansion of a substance is defined as the increase in volume per unit original volume per degree rise in its temperature.
The unit of αv is °C-1 (or) KT-1
Question 10.
What is meant by conduction?
Answer:
Conduction is the process of direct transfer of heat through matter due to temperature difference. When two objects are in direct contact with one another, heat will be transferred from the hotter object to the colder one. The objects which allow heat to travel easily through them are called conductors.
Question 11.
What is meant by Convection?
Answer:
Convection is the process in which heat transfer is by actual movement of molecules in fluids such as liquids and gases. In convection, molecules move freely from one place to another.
![]()
Question 12.
What is meant by Radiation? Give example.
Answer:
Radiation is a form of energy transfer from one body to another by electromagnetic waves.
Example:
1. Solar energy from the Sun.
2. Radiation from room heater.
Question 13.
State Newton’s Law of cooling.
Answer:
Newton’s law of cooling states that the rate of loss of heat of a body is directly proportional to the difference in the temperature between that body and its surroundings.
Question 14.
What do you meant by absolute zero of temperature?
Answer:
The lowest temperature of 0 K at which a gas is supposed to have zero volume (and zero pressure) and at which entire molecular motion stops is called absolute zero of temperature.
Question 15.
State Prevost theory of heat exchange.
Answer:
Prevost theory states that all bodies emit thermal radiation at all temperatures above absolute zero irrespective of the nature of the surroundings.
Question 16.
What is meant by ‘Mechanical equilibrium’?
Answer:
A system is said to be in mechanical equilibrium if no unbalanced force acts on the thermo dynamic system or on the surrounding by thermodynamic system.
Question 17.
What is meant by ‘chemical equilibrium’?
Answer:
Chemical equilibrium: If there is no net chemical reaction between two thermodynamic systems in contact with each other then it is said to be in chemical equilibrium.
Question 18.
What is meant by ‘thermodynamic equilibrium’.
Answer:
In a state of thermodynamic equilibrium the macroscopic variables such as pressure, volume and temperature will have fixed values and do not change with time.
Question 19.
Briefly explain how such a quasi-static process can be carried out.
Answer:
Quasi-static process: Consider a system of an ideal gas kept in a cylinder of volume V at pressure P and temperature T. When the piston attached to the cylinder moves outward the volume of the gas will change. As a result the temperature and pressure will also change because all three variables P,T and V are related by the equation of state PV = NkT. If a block of some mass is kept on the piston, it will suddenly push the piston downward. The pressure near the piston will be larger than other parts of the system. It implies that the gas is in non-equilibrium state. We cannot determine pressure, temperature or internal energy of the system until it reaches another equilibrium state. But if the piston is pushed very slowly such that at every stage it is still in equilibrium with surroundings, we can use the equation of state to calculate the internal energy, pressure or temperature. This kind of process is called quasi-static process.
A quasi-static process is an infinitely slow process in which the system changes its variables (P,V,T) so slowly such that it remains in thermal, mechanical and chemical equilibrium with its surroundings throughout. By this infinite, slow variation, the system is always almost close to equilibrium state.
Question 20.
Define specific heat capacity at constant pressure.
Answer:
Specific heat capacity at constant pressure (sP): The amount of heat energy required to raise the temperature of one kg of a substance by 1 K or 1°C by keeping the pressure constant is called specific heat capacity of at constant pressure.
Question 21.
Define specific heat capacity at constant volume.
Answer:
Specific heat capacity at constant volume (sV): The amount of heat energy required to raise the temperature of one kg of a substance by 1 K or 1°C by keeping the volume constant is called specific heat capacity at constant volume.
Question 22.
Define molar specific heat capacity at constant volume.
Answer:
The amount of heat required to rise the temperature of one mole of a substance by 1K or 1 °C at constant volume is called molar specific heat capacity at constant volume.
Question 23.
Define molar specific heat capacity at constant pressure.
Answer:
The amount of heat required to rise the temperature of one mole of a substance by 1K or 1°C at constant pressure is called molar specific heat capacity at constant pressure.
Question 24.
What is a isobaric process?
Answer:
It is a thermodynamic process which occurs at a constant pressure.
Question 25.
What is a isochoric process?
Answer:
It is a thermodynamic process which occurs at a constant volume.
Samacheer Kalvi 11th Physics Heat and Thermodynamics Numerical Problems
Question 1.
Copper wire of length l increase in length by 1% when heated from temperature T1 to T2. Find the percentage change in area when a copper plate of dimensions 2l × l is heated from T1 to T2
Answer:

Question 2.
A steel rod of length 25 cm has a cross-sectional area of 0.8 cm2. Find the force required to stretch this rod by the same amount as the expansion produced by heating it through 10°C. (coefficient of linear expansion of steel is 10-5/°C and Young’s modulus of steel is 2 × 1010Nm-2)
Answer:
![]()
Question 3.
The temperature at the bottom of a 40 m deap lake is 12°C and that at the surface is 35°C. An air bubble of volume 1.0 cm3 rises from the bottom to the surface. Find its volume, (atmospheric pressure = 10 m of water)
Answer:
Let P1, V1 and T1 be the pressure, bubble volume and absolute temperature at the bottom of the lake and let P2, V2 and T2 be the corresponding quantities at the surface. Then
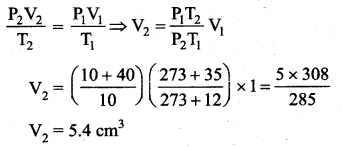
Question 4.
Ajar ‘A’ is filled with an ideal gas characterised by parameters P, V and T and another jar B is filled with an ideal gas with parameters 2P, \(\frac{\mathrm{V}}{4}\) and 2T. Find the ratio of the number of molecules in jar A and B.
Answer:
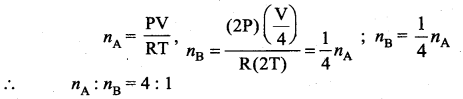
Question 5.
By what percentage should the pressure of a given mass of a gas be increased so as to decrease its volume by 10% at a constant temperature?
Answer:
According to Boyle’s law,

![]()
Question 6.
A flask is filled with 13g of an ideal gas at 27°C and its temperature is raised to 52°C. Find the mass of the gas that hias to be released to maintain the temperature of the gas in the flask at 52°C and the pressure is same as the initial pressure.
Answer:
Let n be the initial number of moles and ri be the final number of moles. Since pressure and volume remain the same, we have
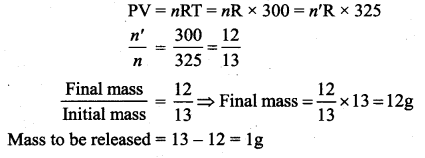
Question 7.
A rod of metal-1 of length 50.0 cm elongates by 0.10 cm when it is heated from 0°C to 100°C. Another rod of metal-2 of length 80.0 cm elongates by 0.08 cm for the same rise in temperature. A third rod of length 50.0 cm, made by welding pieces of rod 1 rad and 2 rad placed end to end, elongates by 0.03 cm when it is heated from 0°C to 50°C. Then what is the length of metal-1 in the third rod at 0°C?
Answer:
For metal-1, For metal-2,

Let the lengths of metal-1 and metal- 2 in the third rod at 0°C be l1 and l2, respectively.
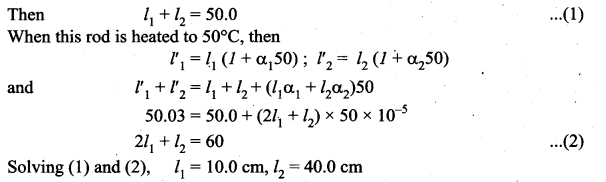
Question 8.
A balloon is filled at 27°C and 1 atm pressure by 500 m3 He. Then find the volume of He at -3°C and 0.5 mm Hg pressure.
Answer:

Question 9.
During an experiment an ideal gas is found to obey an additional law VP2 = constant. The gas is initially at temperature T and Volume V. Find the resulting temperature when it expands to volume 2V.
Answer:

Question 10.
Two vessels separately contain two ideal gases A and B at the same temperature, the pressure of A being twice that of B. Under such conditions, the density of A is found to be 1.5 times the density of B. The ratio of molecular weights of A and B is:
Answer:
According to the ideal gas equation for one mole,
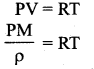
Where ρ is the density and M is the molecular weight of the gas.

Question 11.
For a gas the difference between the two specific heats is 4150 J/Kg K. What is the specific heat of the gas at constant volume if the ratio of specific heat is 1.4?
Answer:

Question 12.
A mass of ideal gas at pressure P is expanded isothermally to four times the original volume and then slowly compressed adiabatically to its original volume. Assuming γ(= CP/CV) to be 1.5, find the new pressure of the gas.
Answer:
Let the initial volume be V. After isothermal expansion, pressure = \(\frac{P}{4}\), volume = 4V
Let P’ is the pressure after adiabatic compression. The volume then is V. Therefore,
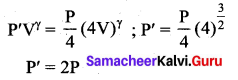
Question 13.
A carnot engine operating between temperature T1 and T2 has efficiency \(\frac{1}{6}\). When T2 is lowered by 62 K, its efficiency increases to \(\frac{1}{3}\). Then find the values of T1 and T2.
Answer:


Question 14.
A perfect gas goes from state A to state B by absorbing 8 × 105 J of heat and doing 6.5 × 105 J of external work. It is now transferred between the same two states in another process in which it absorbs 10s J of heat. In second process. Find the work done in the second process.
Answer:
According to the first law of thermodynamics
∆U = ∆Q – ∆W
In the first process ∆U = 8 × 105 – 6.5 × 105 = 1.5 × 105 J
Now ∆U, being a state function, remains the same in the second process,
∆W = ∆Q – ∆U = 1 × 105 – 1.5 × 105
∆W = – 0.5 × 105J
The negative sign shows that work is done on the gas.
Question 15.
A carnot engine, having efficiency of \(\eta=\frac{1}{10}\) as heat engine, is used as a refrigerator. If the work done on the system is 10 J, then find the amount of energy absorbed from the reservoir at lower temperature.
Answer:
As heat engine, let Q1 be the heat energy absorbed from the source and Q2 be the energy rejected to the sink. Then
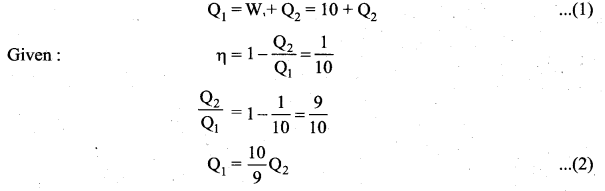
From equation (1) and (2),
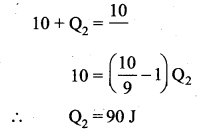
Question 16.
An ideal gas compressed to half its initial volume by means of several processes. Which of the process results in the maximum work done on the gas?
Answer:
Work done on the gas = Area under the curve
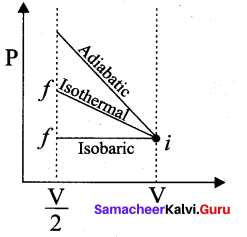
Wadiabatic > Wisothermal > Wisobaric
Wisochoric is obviously zero because in an isochoric process there is no change in Volume.