You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 9 Limits and Continuity Ex 9.3
Question 1.
(a) Find the left right limits of f(x) = \(\frac{x^{2}-4}{\left(x^{2}+4 x+4\right)(x+3)}\) at x = -2
(b) f(x) = tan x at x = \(\frac{\pi}{2}\)
Solution:
(a) f(x) = \(\frac{x^{2}-4}{\left(x^{2}+4 x+4\right)(x+3)}\) at x → -2
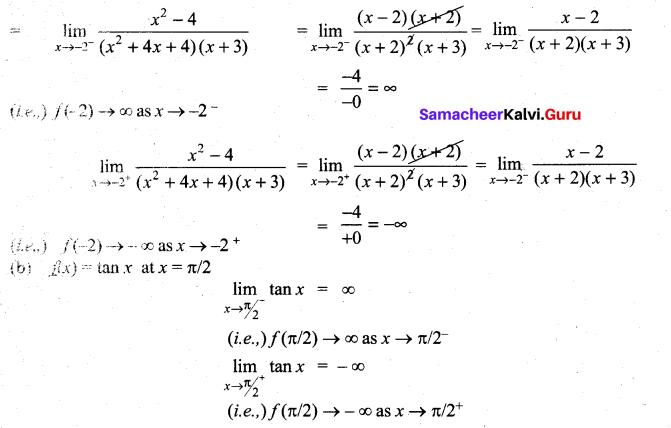
Evaluate the following limits
Question 2.
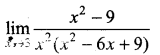
Solution:

Question 3.
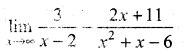
Solution:
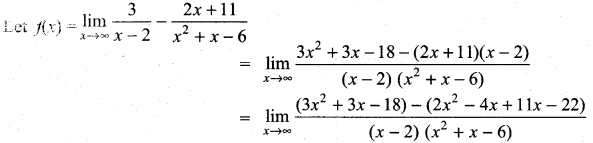
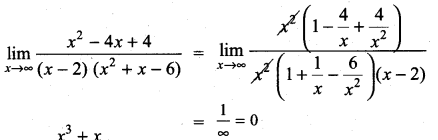
![]()
Question 4.
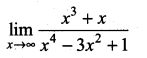
Solution:
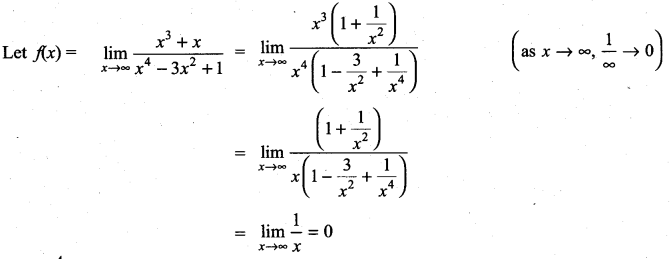
Question 5.
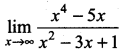
Solution:
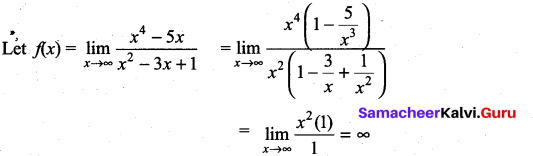
f(x) → ∞ as x → ∞
Question 6.
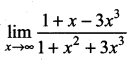
Solution:
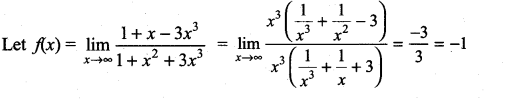
Question 7.
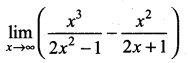
Solution:
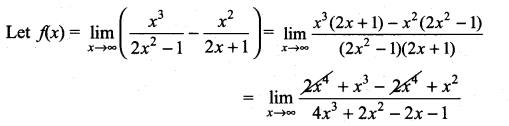
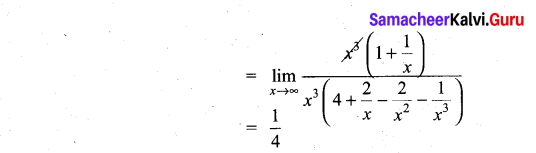
Question 8.
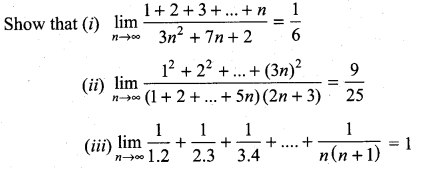
Solution:

![]()
Question 9.
An important problem in fishery science is to estimate the number of fish presently spawning in streams and use this information to predict the number of mature fish or “recruits” that will return to the rivers during the reproductive period. If S is the number of spawners and R the number of recruits, “Beverton-Holt spawner recruit function” is R(S) = \(\frac{S}{(\alpha S+\beta)}\) where α and β are positive constants. Show that this function predicts approximately constant recruitment when the number of spawners is sufficiently large.
Solution:
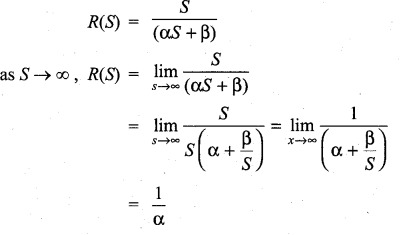
Question 10.
A tank contains 5000 litres of pure water. Brine (very salty water) that contains 30 grams of salt per litre of water is pumped into the tank at a rate of 25 litres per minute. The concentration of saltwater after t minutes (in grams per litre) is C(t) = \(\frac{30 t}{200+t}\). What happens to the concentration as t → ∞?
Solution:

Samacheer Kalvi 11th Maths Solutions Chapter 9 Limits and Continuity Ex 9.3 Additional Problems
Question 1.
Evaluate ![]()
Solution:
The given expression is of the form ∞ – ∞. So we first write it in the rational form \(\frac{f(x)}{g(x)}\). So that it reduces to either \(\frac{0}{0}\) form or \(\frac{\infty}{\infty}\) form.
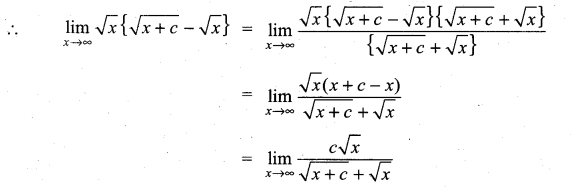
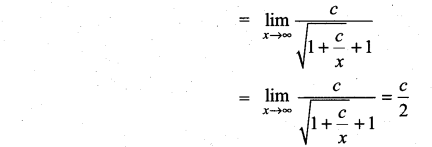
Question 2.
Evaluate: ![]()
Solution:
Here the expression assumes the form ∞ – ∞ as x → ∞. So, we first reduce it to the rational form \(\frac{f(x)}{g(x)}\)
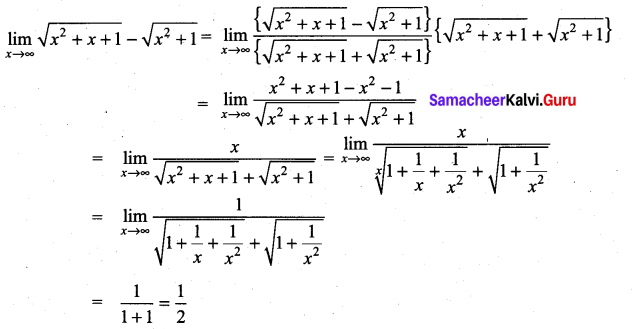
Question 3.
Evaluate 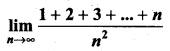
Solution:
We have
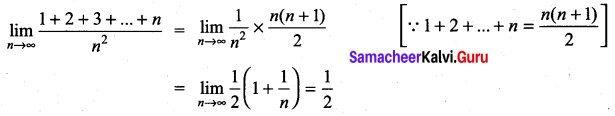
Question 4.
Evaluate: 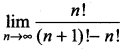
Solution:
We have,
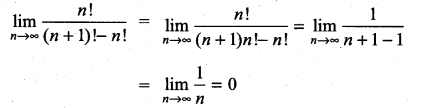
![]()
Question 5.
Evaluate: 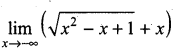
Solution:

Question 6.
Evaluate: 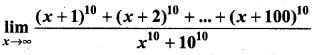
Solution:
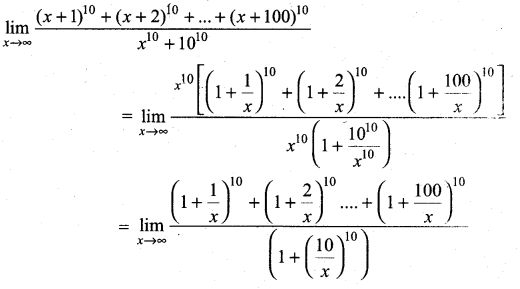
![]()