Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.12

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.12

Question 1.
Let b > 0 and b ≠ 1. Express y = b^x in logarithmic form. Also, state the domain and range of the logarithmic function.
Solution:
Given y = b^x
By the definition of logarithm log_b y = x
The domain of a logarithmic function is the set of positive real numbers and the range is the set of real numbers.

Question 2.
Compute log₉27 – log₂₇9.
Solution:
Let log₉27 = x ⇒ 27 = 9^x ⇒ 3³ = (3²)^x = 3^2x
⇒ 2x = 3 ⇒ x = 3/2
Let log₂₇9 = x

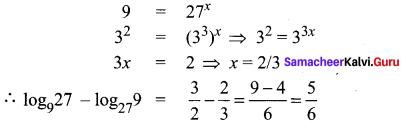
Question 3.
Solve log₈x + log₄x + log₂x = 11
Solution:

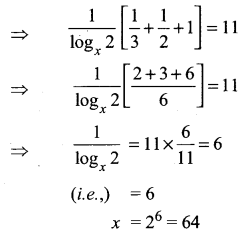
Question 4.

Solution:

Question 5.

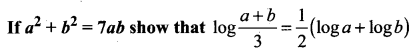
Solution:

Question 6.

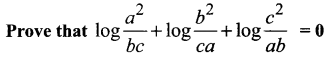
Solution:

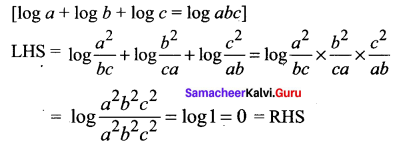
Another method

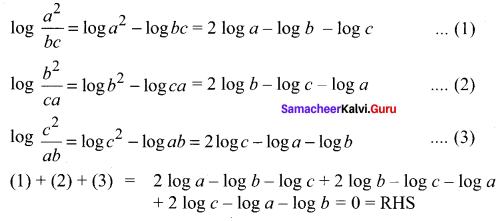
Question 7.

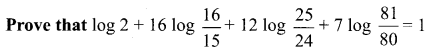
Solution:

Question 8.

Solution:

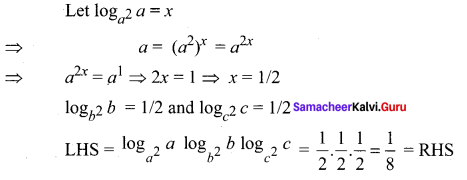
Question 9.

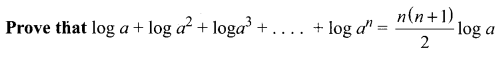
Solution:

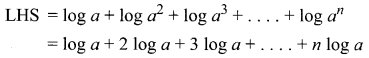
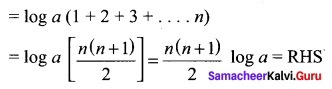
Question 10.

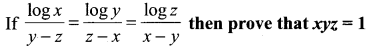
Solution:

Question 11.

Solution:

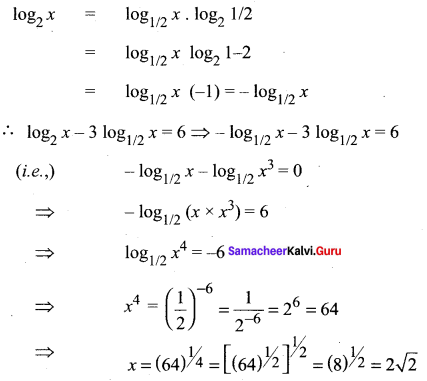
Question 12.
Solve log_{5 – x}(x² – 6x + 65) = 2
Solution:
Given log_{5 – x} (x² – 6x + 65) = 2
By the definition of logarithm
x² – 6x + 65 = (5 – x)²
x² – 6x + 65 = 25 – 10x + x²
10x – 6x + 65 – 25 = 0
4x + 40 = 0
4x = – 40
x = \(-\frac{40}{4}\) = -10
x = -10

Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.12 Additional Questions

Question 1.

Solution:

Question 2.

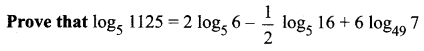
Solution:

Question 3.

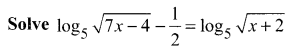
Solution:

Question 4.

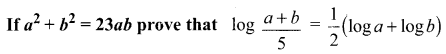
Solution: