You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 12 Introduction to Probability Theory Ex 12.3
Question 1.
Can two events be mutually exclusive and independent simultaneously?
Solution:
No. If two events are mutually exclusive, they cannot be independent.
Question 2.
If A and B are two events such that P(A ∪ B) = 0.7, P(A ∩ B) = 0.2, and P(B) = 0.5 then show that A and B are independent.
Solution:
GivenP(A ∪ B) = 0.7, P(A ∩ B)= 0.2 and P(B) = 0.5
To find P(A)
Now, P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
(i.e.,) 0.7 = P(A) + 0.5 – 0.2
⇒ 0.7 – 0.5 + 0.2 = P(A)
(i.e.,) P(A) = 0.4
Now P(A ∩ B) = 0.2 …………. (i)
P(A) P(B) = 0.4 × 0.5 = 0.2 ………… (ii)
(1) = (2) ⇒ P(A ∩ B) = P(A) P(B)
⇒ A and B are independent.
Question 3.
If A and B are two independent events such that P(A ∪ B) = 0.6, P(A) = 0.2, find P(B).
Solution:
Given A and B are two independent events such that
P(A ∪ B) = 0.6, P(A) = 0.2
Since A and B are independent, we have
P(A ∩ B) = P(A) . P(B)
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
P(A ∪ B) = P(A) + P(B) – P(A) P(B)
0.6 = 0.2 + P(B) – 0.2 P(B)
0.6 – 0.2 = (1 – 0.2) P (B)
0.4 = 0.8 P(B)
P(B) = \(\frac{0.4}{0.8}\)
P(B) = \(\frac{4}{8}\) = \(\frac{1}{2}\) = 0.5
![]()
Question 4.
If P(A) = 0.5, P(B) = 0.8 and P(B/A) = 0.8, find (P(A/B)) and P(A ∪ B)
Solution:
Given P(A) = 0.5, P(B) = 0.8 and P(B/A) = 0.8 to find P(A/B) & P(A ∪ B)

So, P(A/B) =0.5 and P(A ∪ B) = 0.9.
Question 5.
If for two events A and B, P(A) = \(\frac{3}{4}\), P(B) = \(\frac{2}{5}\) and A ∪ B = S (sample space), find the conditional probability P(A/B).
Solution:
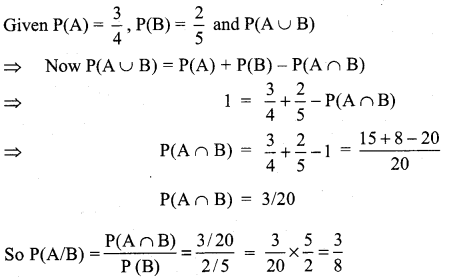
Question 6.
A problem in Mathematics is given to three students whose chances of solving it are \(\frac{1}{3}, \frac{1}{4}\) and\(\frac{1}{5}\)
(i) What is the probability that the problem is solved?
(ii) What is the probability that exactly one of them will solve it?
Solution:
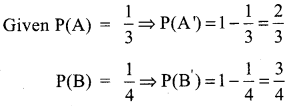
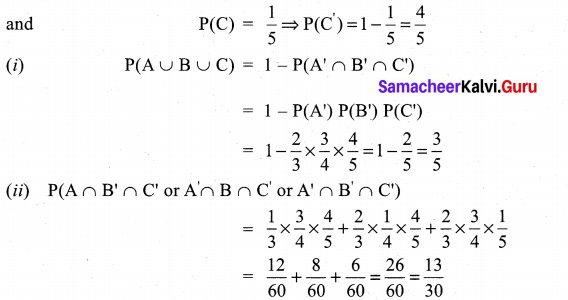
Question 7.
The probability that a car being filled with petrol will also need an oil change is 0.30; the probability that it needs a new oil filter is 0.40, and the probability that both the oil and filter need changing is 0.15.
(i) If the oil had to be changed, what is the probability that a new oil filter is needed?
(ii) If a new oil filter is needed, what is the probability that the oil has to be changed?
Solution:
Given P(A) = 0.3, P(B) = 0.4 and P(A ∩ B) = 0.15
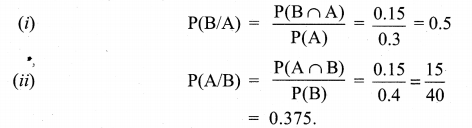
Question 8.
One bag contains 5 white and 3 black balls. Another bag contains 4 white and 6 black balls. If one ball is drawn from each bag, find the probability that (i) both are white (ii) both are black (iii) one white and one black.
Solution:
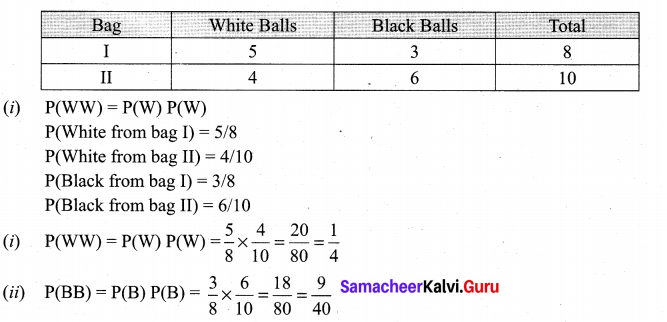
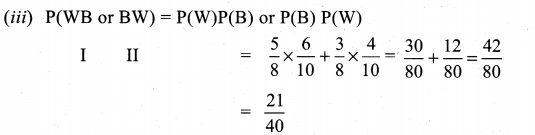
![]()
Question 9.
Two-thirds of students in a class are boys and the rest girls. It is known that the probability of a girl getting the first grade is 0.85 and that of boys is 0.70. Find the probability that a student chosen at random will get first-grade marks.
Solution:

Question 10.
Given P(A) = 0.4 and P(A ∪ B) = 0.7. Find P(B) if
(i) A and B are mutually exclusive
(ii) A and B are independent events
(iii) P(A/B) = 0.4
(iv) P(B/A) = 0.5
Solution:
Given P(A) = 0.4 and P(A ∪ B) = 0.7
(i) A and B are mutually exclusive
∴ A ∩ B = Φ and P(A ∩ B) = 0
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
P(A ∪ B) = P(A) + P(B)
0.7 = 0.4 + P(B)
P(B) = 0.7 – 0.4 = 0.3
(ii) A and B are independent events
∴ P(A ∩ B) = P(A) . P(B)
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
P(A ∪ B) = P(A) + P(B) – P(A) . P(B)
0.7 = 0.4 + P(B) – 0.4 . P(B)
0.7 – 0.4 = P( B) (1 – 0.4)
0.3 = 0.6 × P(B)
P(B) = \(\frac{0.3}{0.6}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\)
P(B) = 0.5
(iii) P(A/B) = 0.4
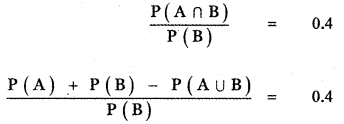
P(A) + P(B) – P(A ∪ B) = 0.4 P(B)
0.4 + P ( B) – 0.7. = 0.4 P (B)
P(B) – 0.3 = 0.4 P(B)
P(B) – 0.4 P(B) = 0.3
(1 – 0.4)P(B) = 0.3
0.6 P(B) = 0.3
P(B) = \(\frac{0.3}{0.6}\) = \(\frac{3}{6}\)
P(B) = \(\frac{1}{2}\) = 0.5
(iv) P(B/A) = 0.5
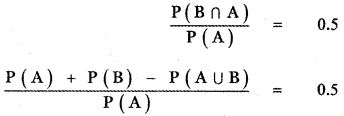
P(A) + P(B) – P(A ∪ B) = 0.5 . P(A)
0.4 + P(B) – 0.7 = 0.5 × 0.4
P(B) – 0.3 = 0.2
P(B) = 0.2 + 0.3
P(B) = 0.5
![]()
Question 11.
A year is selected at random. What is the probability that (i) it contains 53 Sundays (ii) it is a leap year which contains 53 Sundays?
Solution:
(i) A non-leap year contains 365 \(\frac{1}{4}\) days 365\(\frac{1}{4}\) ÷ 7 = 52 weeks + 1\(\frac{1}{4}\) days. In 52 weeks,
we get 52 Sundays from the remaining 1\(\frac{1}{4}\) days we should get one sunday.
∴ The probability of getting the day as Sunday = \(\frac{5 / 4}{7}=\frac{5}{4 \times 7}=\frac{5}{28}\)
(ii) It is a leap year which contaIns 53 Sundays.
A leap year contains 366 days.
366 days = 52 weeks + 2 days.
52 weeks contain 52 Sundays
So in order to get 53 Sundays in a leap year, the remaining 2 days must contain a Sunday.
The remaining 2 days may be off from
S = {(Sunday, Monday), (Monday, Tuesday), (Tuesday, Wednesday), ( Wednesday, Thursday), (Thursday, Friday), (Friday, Saturday), (Saturday, Sunday) }
n(S) = 7
Let A be the event getting a Sunday
A = {(Sunday, Monday) , (Saturday, Sunday)}
n(A) = 2
Probability of getting a Sunday from the remaining 2 days
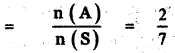
Probability of getting 53 Sundays in a leap year = Probability of getting a leap year × Probability of getting a Sunday from the remaining 2 days
= \(\frac{1}{4}\) × \(\frac{2}{7}\) = \(\frac{1}{14}\)
∴ Probability of getting 53 Sundays in a leap year = \(\frac{1}{14}\)
Question 12.
Suppose the chances of hitting a target by a person X is 3 times in 4 shots, by Y is 4 times in 5 shots, and by Z is 2 times in 3 shots. They fire simultaneously exactly one time. What is the probability that the target is damaged by exactly 2 hits?
Solution:
Given P(X) = 3/4, P(X’) = 1 – 3/4 = 1/4
∴ P(Y) = 4/5, P(Y’) = 1 – 4/5 = 1/5
P(Z) = \(\frac{2}{3}\) ∴ P(Z’) = 1 – \(\frac{2}{3}\) = \(\frac{1}{3}\)
P(X ∩ Y ∩ Z’) + P(X ∩ Y’ ∩ Z) + P(X’ ∩ Y ∩ Z)
= \(\frac{3}{4} \times \frac{4}{5} \times \frac{1}{3}+\frac{3}{4} \times \frac{1}{5} \times \frac{2}{3}+\frac{1}{4} \times \frac{4}{5} \times \frac{2}{3}\)
= \(\frac{12}{60}+\frac{6}{60}+\frac{8}{60}=\frac{26}{60}=\frac{13}{30}\)
Samacheer Kalvi 11th Maths Solutions Chapter 12 Introduction to Probability Theory Ex 12.3 Additional Problems
Question 1.
If P(A) = 0.4, P(B) = 0.7 and P(B/A) = 0.5, find P(A /B) and P(A ∪ B).
Solution:
P(B/A) = 0.5 ⇒ \(\frac{\mathrm{P}(\mathrm{B} \cap \mathrm{A})}{\mathrm{P}(\mathrm{A})}\) = 0.5
(i.e.,) \(\frac{\mathrm{P}(\mathrm{B} \cap \mathrm{A})}{0.4}\) = 0.5
∴ P(B ∩ A) = 0.4 × 0.5 = 0.2
(i.e.,) P(A ∩ B)= 0.2
P(A ∪ B)= P(A) + P(B) – P(A ∩ B)
P(A ∪ B) = 0.4 + 0.7 – 0.2 = 0.9
P(A/B) = \(\frac{P(A \cap B)}{P(B)}=\frac{0.2}{0.7}=\frac{2}{7}\)
Question 2.
If A and B are two events such that P(A ∪ B) = \(\frac{5}{6}\), P(A ∩ B) = \(\frac{1}{3}\), P(\(\overline{B}\)) = \(\frac{1}{2}\) show that A and B are independent.
Solution:
P(\(\overline{B}\)) = \(\frac{1}{2}\) (i.e.,)1 – P(B) = \(\frac{1}{2}\)

∴ A and B are independent
Question 3.
P(A) = 0.3, P(B) = 0.6 and P(A ∩ B) = 0.25. Find
(i) P(A ∪ B)
(ii) P(A/B)
(iii) P(B/\(\overline{\mathrm{A}}\))
(iv) \(\mathrm{P}(\overline{\mathrm{A}} / \mathrm{B})\)
(v) \(\mathrm{P}(\overline{\mathrm{A}} / \overline{\mathrm{B}})\)
Solution:

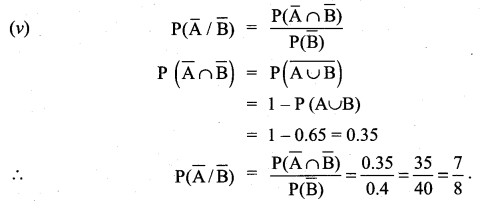
![]()
Question 4.
Two cards are drawn one by one at random from a deck of 52 playing cards. What is the – probability Of getting two jacks if (i) the first card is replaced before the second card is drawn
(ii) the first card is not replaced before the second card is drawn?
Solution:
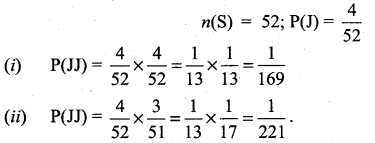
Question 5.
A husband and wife appear in an interview for two vacancies in the same post. The probability of husband’s selection is \(\frac{1}{6}\) and that of wife’s selection is \(\frac{1}{5}\). What is the probability that
(i) both of them will be selected
(ii) only one of them will be selected
(iii) none of them will be selected?
Solution:
P(H) = Probability of husband’s selection = \(\frac{1}{6}\)
P(W) = Probability of wife’s selection = \(\frac{1}{5}\)
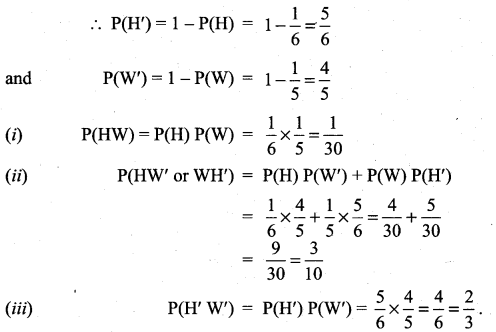
Question 6.
For a student, the probability of getting admission to IIT is 60% and the probability of getting admission to Anna university is 75%. Find the probability that
(i) getting admission in only one of these
(ii) getting admission in atleast one of these.
Solution:
