Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Ex 2.8

You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Ex 2.8

Question 1.
Find the sum of first n terms of the G.P.
(i) 5, -3, \(\frac { 9 }{ 5 } \), – \(\frac { 27 }{ 25 } \), ……….
(ii) 256, 64, 16, ……..
Solution:
(i) 5, -3, \(\frac { 9 }{ 5 } \), \(\frac { -27 }{ 25 } \), ………

(ii) 256, 64, 16,…….
a = 256

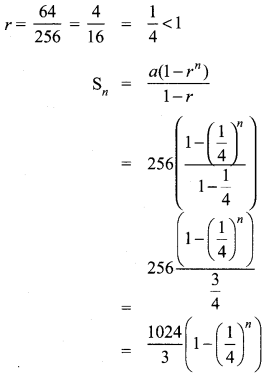
Question 2.
Find the sum of first six terms of the G.P. 5, 15, 45, …
Solution:
G.P.= 5, 15, 45, 15

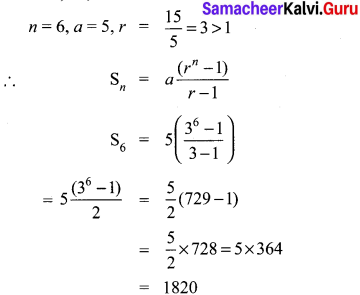
Question 3.
Find the first term of the GP. whose common ratio 5 and whose sum to first 6 terms is 46872.
Solution:
Common ratio, r = 5
S₆ = 46872

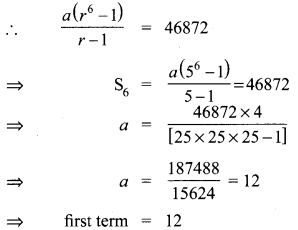
Question 4.
Find the sum to infinity of (i) 9 + 3 + 1 + ….
(ii) 21 + 14 + \(\frac { 28 }{ 3 } \) + ….
Solution:
(i) 9 + 3 + 1 + ….

(ii) 21 + 14 + \(\frac { 28 }{ 3 } \) + ….

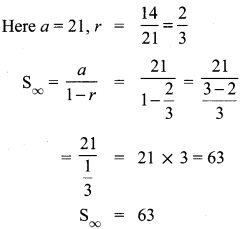
Question 5.
If the first term of an infinite G.P. is 8 and its sum to infinity is \(\frac { 32 }{ 3 } \) then find the common ratio.
Solution:
a = 8

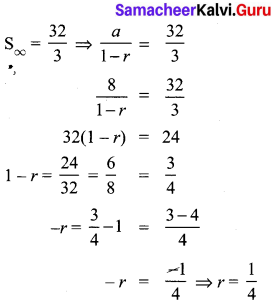
Question 6.
Find the sum to n terms of the series
(i) 0.4 + 0.44 + 0.444 +…. to n terms
(ii) 3 + 33 + 333 + …. to n terms
Solution:
(i) 0.4 + 0.44 + 0.444 + … to n terms
= 4 (0.1 + 0.11 + 0.111 + … to n terms)
= \(\frac { 4 }{ 9 } \) (0.9 + 0.99 + 0.999 + … to n terms)
= \(\frac { 4 }{ 9 } \) (1 -0.1) + (1 – 0.01) +(1 – 0.001) + … n terms)

(ii) 3 + 33 + 333 + … to n terms.
= 3 (1 + 11 + 111 + …….. to n terms)
= \(\frac { 3 }{ 9 } \) (9 + 99 + 999 +… to n terms)
\(\frac { 1 }{ 3 } \) = [(10 – 1) + (100 – 1) + (1000 – 1) + … to n terms]
= \(\frac { 1 }{ 3 } \) [(10 + 100 + 1000 + .. ) + (-1)n]

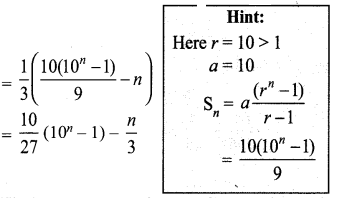
Question 7.
Find the sum of the Geometric series
3 + 6 + 12 + …… + 1536.
Solution:
3 + 6 + 12 + …… + 1536
Here a = 3

Question 8.
Kumar writes a letter to four of his friends. He asks each one of them to copy the letter and mail to four different persons with the instruction that they continue the process similarly. Assuming that the process is unaltered and it costs ₹2 to mail one letter, find the amount spent on postage when 8th set of letters is mailed.

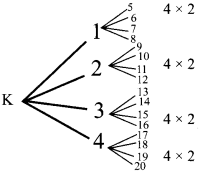
Solution:
Kumar (1) 2 × 4
Cost of posting 1^st set of Letters.
Cost of posting 2^nd set of letters

Amount spent
[a + ar + ar² +… ar^n-1]
= 4 [2 + 2 × 4 + 2 × 42 ÷ + 2 × 4⁷]
= 4 [S_n] Here n = 8, r = 4
It is a G.P

∴ Cost of postage after posting 8th set of letters
= 4 × 43690 = ₹ 174760

Question 9.
Find the rational form of the number 0.\(\overline{123}\)
Solution:
Let x = 0.123123123 ………. ⇒ x = 0.\(\overline{123}\) …..(1)
Multiplying 1000 on both rides
1000 x = 123.123123… ⇒ 1000x = 123.\(\overline{123}\) …..(2)
(2) – (1) = 1000x – x 123.\(\overline{123}\) – 0.\(\overline{123}\).
⇒ 999 x = 123
⇒ x = \(\frac { 123 }{ 999 } \)
⇒ x = \(\frac { 41 }{ 333 } \) Rational number

Question 10.
If Sn = (x + y)+(x² + xy + y²) + (x³ + x²y + xy² + y³) + …n terms then prove that (x – y)

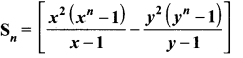
Solution:
Sn = (x + y) + (x² + xy + y²) + (x³ + x²y + xy² + y³) + …n terms
⇒ x. S_n = (x + y)x + (x² + xy + y²)x + (x³ + x²y + xy² + y³) x + ….
⇒ x. S_n = x² +xy + x³ + x²y + y²x + x⁴ + x³y
+ x² y² + y³ x +…… ….(1)
Multiplying ‘y’ on both sides,
= y.S_n = (x + y)y + (x² + xy + y²) y+
(x³ + x²y + xy² + y³) y + ….
= y.S_n = xy + y² + x²y + xy² + y³ + x³y
+ x³y + x²y² + xy³ + y⁴ + ……….
(1) – (2) ⇒